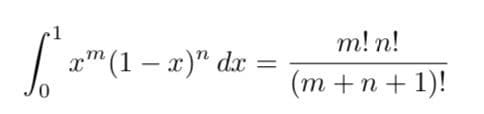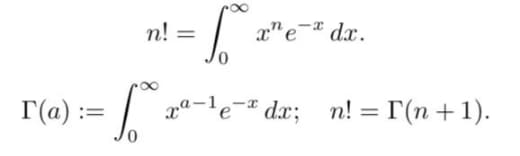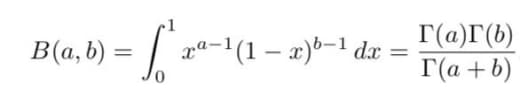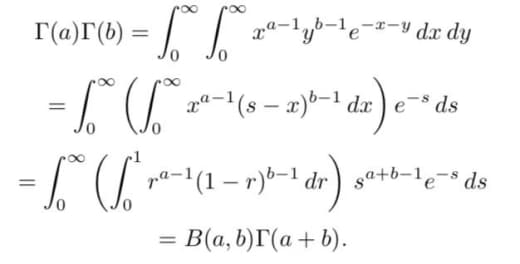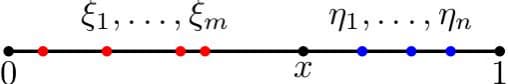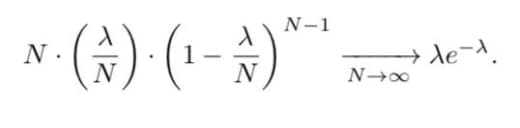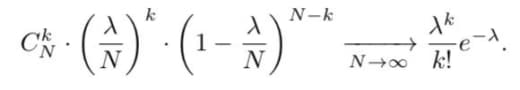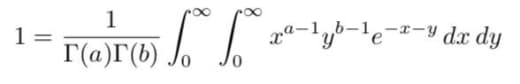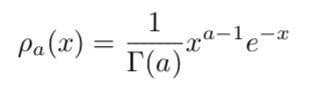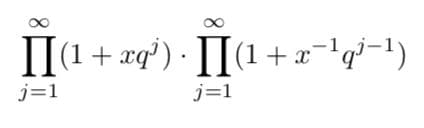оглавление (избранные ссылки)
15 August 2019
М
11:33
Математические байки
Начнём, пожалуй :)
Victor Kleptsyn
М
11:33
Математические байки
Вчера из доклада Бунимовича узнал о забавной игре.
Пусть много раз подкидывается честная монетка, а игроки выбирают (разные) слова из "О" и "Р" (орёл и решка). Чьё слово выпало первым, тот выиграл.
Пусть много раз подкидывается честная монетка, а игроки выбирают (разные) слова из "О" и "Р" (орёл и решка). Чьё слово выпало первым, тот выиграл.
Victor Kleptsyn
М
11:34
Математические байки
Понятно, что если первый игрок сказал "О", а второй "Р", то монетку потребуется подкинуть только один раз, и шансы на выигрыш у игроков одинаковые.
Victor Kleptsyn
М
11:34
Математические байки
А что, если слова более длинные?
Victor Kleptsyn
М
11:36
Математические байки
Оказывается, что игра получается нетранзитивной, и какого-либо "самого лучшего слова" нет. А именно — пусть слова должны быть одинаковой длины n, не меньшей трёх, и сначала первый игрок говорит своё слово, а потом второй выбирает своё.
Victor Kleptsyn
М
11:37
Математические байки
Так вот — тогда, какое бы слово первый игрок не назвал, второй может ответить так, чтобы иметь вероятность выигрыша, строго большую (1/2).
Victor Kleptsyn
М
11:37
Математические байки
Пример: пусть первый игрок называет ООО.
Victor Kleptsyn
М
11:38
Математические байки
Ответ второго — РОО, и его вероятность выигрыша — 7/8(!).
Victor Kleptsyn
М
11:38
Математические байки
Действительно, первый тогда может выиграть _только_ если на первых трёх подбрасываниях выпадут три орла.
Victor Kleptsyn
М
11:39
Математические байки
Если этого не произошло — то выпала хотя бы одна решка, и дальше второй всегда выиграет за шаг до того, как у первого будет хотя бы шанс выкинуть третьего орла
Victor Kleptsyn
М
11:39
Математические байки
(В первый раз, когда выпадут два орла подряд, перед ними должна быть решка — иначе это не первый раз — и вот второй и выиграл)
Victor Kleptsyn
М
11:40
Математические байки
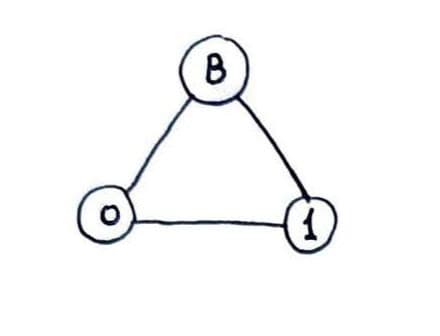
Так вот — игра как "камень-ножницы-бумага", на любое слово первого у второго есть выгодный ответ.
Victor Kleptsyn
М
11:42
Математические байки
Называется она "Penney's game" (https://en.wikipedia.org/wiki/Penney%27s_game ), а формулу для отношения вероятностей выигрыша игроков придумал Конвей.
Victor Kleptsyn
М
12:56
Математические байки
Формула, кстати, очень интересная.
Victor Kleptsyn
М
12:57
Математические байки
Сначала для пары слов A, B (пусть пока одинаковой длины) сделаем следующее: напишем B под A, будем сдвигать его на 1 вправо на каждом шаге, и будем писать 1, если на пересечении они совпадают, а 0, если нет.
Victor Kleptsyn
М
12:57
Математические байки
Например: A=РООР, B=ОРОР.
РООР
ОРОР
не совпадают — пишем 0.
РООР
ОРОР
не совпадают — пишем 0.
Victor Kleptsyn
М
12:57
Математические байки
РООР
-ОРОР
на пересечении не совпадают — пишем 0.
-ОРОР
на пересечении не совпадают — пишем 0.
Victor Kleptsyn
М
12:58
Математические байки
РООР
--ОРОР
А вот теперь совпадают, ОР=ОР, пишем 1
--ОРОР
А вот теперь совпадают, ОР=ОР, пишем 1
Victor Kleptsyn
М
12:58
Математические байки
РООР
---ОРОР
опять не совпадают, пишем 0
---ОРОР
опять не совпадают, пишем 0
Victor Kleptsyn
М
12:58
Математические байки
Получается 0010. А теперь интерпретируем это как двоичную запись числа — и полученное число обозначим как (A,B). То есть мы только что посчитали, что
(РООР, ОРОР) = 2.
(РООР, ОРОР) = 2.
Victor Kleptsyn
М
12:59
Математические байки
Формула Конвея:
Victor Kleptsyn
М
12:59
Математические байки
шансы на победу у слов B и A относятся, как
(A,A)-(A,B) к (B,B)-(B,A).
(A,A)-(A,B) к (B,B)-(B,A).
Victor Kleptsyn
М
13:00
Математические байки
Например, для A=ООО, B=РОО, легко посчитать, что
(A,A)={111}_2 = 7,
(A,A)={111}_2 = 7,
Victor Kleptsyn
М
13:00
Математические байки
(A,B)={000}_2= 0,
Victor Kleptsyn
М
13:00
Математические байки
(B,A)={011}_2= 3,
Victor Kleptsyn
М
13:00
Математические байки
(B,B)={100}_2 = 4.
Victor Kleptsyn
М
13:01
Математические байки
Получаем
(7-0):(4-3) = 7:1,
как мы уже видели в самом начале.
(7-0):(4-3) = 7:1,
как мы уже видели в самом начале.
Victor Kleptsyn
М
13:11
Математические байки
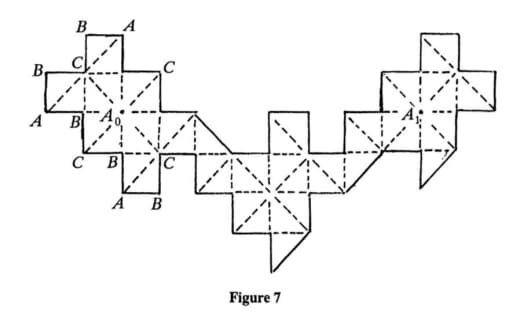
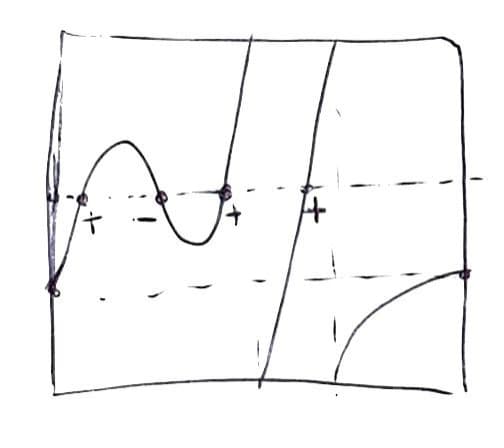
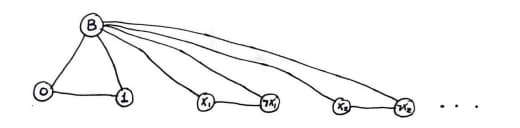
Иллюстрация из статьи Мартина Гарднера "On the paradoxical situations that arise from nontransitive relations" в колонке "Mathematical Games", Scientific American, октябрь 1974
Victor Kleptsyn
М
13:11
Математические байки
(а H и T тут — от английских Head и Tail)
Victor Kleptsyn
М
15:05
Математические байки
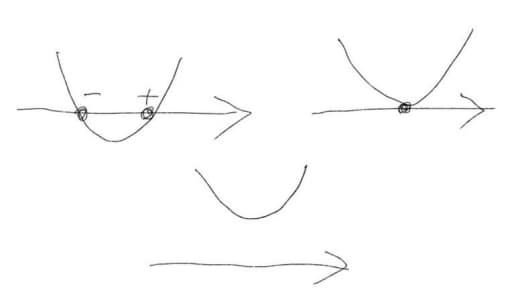
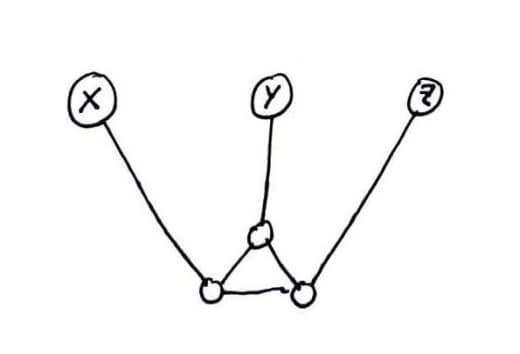
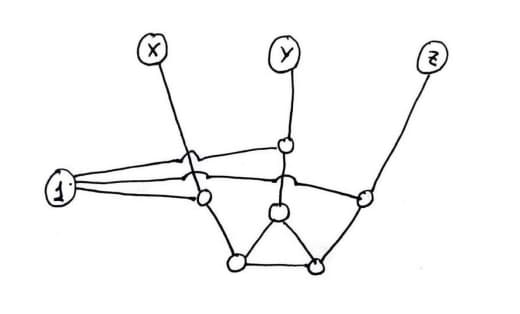
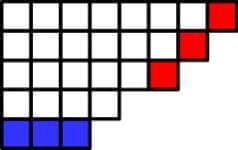
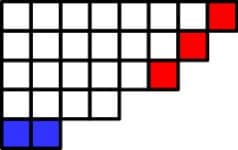
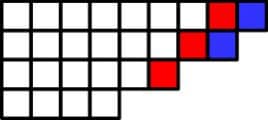
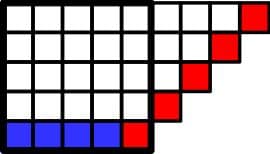
Картинка из той же статьи — как играть для слов длины 3 (красным выделены оптимальные ответы):
Victor Kleptsyn
М
17:16
Математические байки
Ну и прекрасная цитата из той же статьи Гарднера —
Victor Kleptsyn
М
М
18:37
Математические байки
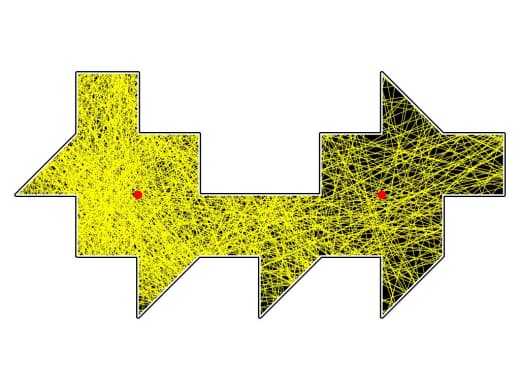
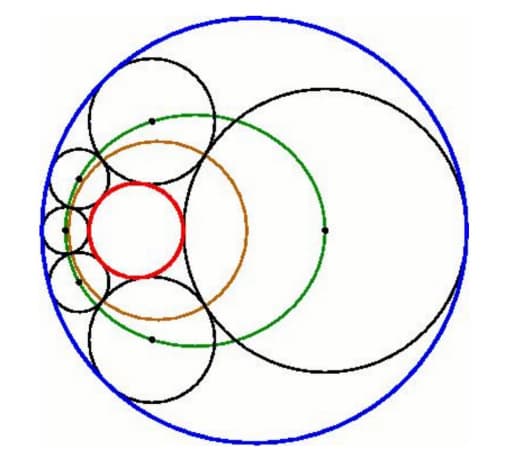
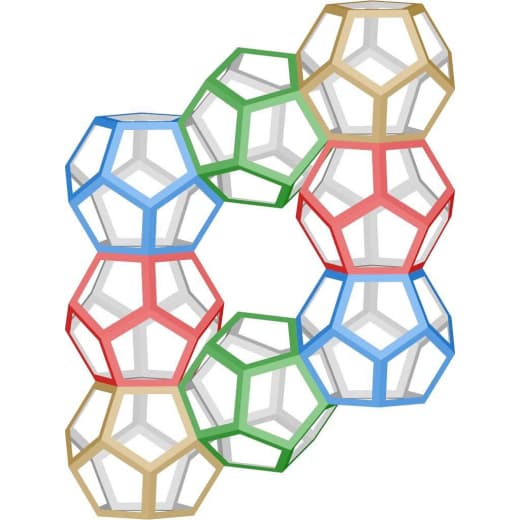
Да — возвращаясь к началу, Бунимович занимается динамическими системами и бильярдами. Скажем, одна из известных систем — "стадион Бунимовича":
https://blogs.ams.org/visualinsight/2016/11/15/bunimovich-stadium/
https://blogs.ams.org/visualinsight/2016/11/15/bunimovich-stadium/
Victor Kleptsyn
М
18:37
Математические байки
Бильярдные траектории в (строго) выпуклых областях ведут себя более-менее регулярно, а в (кусочно) вогнутых — хаотично.
Victor Kleptsyn
М
18:37
Математические байки
Но оказывается, что если построить по полукругу на противоположных сторонах прямоугольника, то в получившемся "стадионе" бильярдные траектории летают как раз таки хаотично — а не регулярно, как можно было бы подумать, исходя из его выпуклости.
Victor Kleptsyn
М
18:43
Математические байки
Так вот — почему же Бунимович эту игру вспомнил? Дело в том, что для динамических систем один из стандартных инструментов это кодирование точки — сопоставление ей последовательности символов.
Victor Kleptsyn
М
18:44
Математические байки
Один из самых основных примеров — это отображение F:x->{2x} отрезка [0,1] в себя.
Victor Kleptsyn
М
18:50
Математические байки
Оно хаотично: если взять две точки очень близко друг к другу, и начать применять F — то на каждой итерации расстояния между точками будут удваиваться. (Тут удобнее вместо отрезка рассмотреть окружность, склеив 0 и 1 — тогда отображение становится непрерывным, и удваивающим угол; кстати, если нарисовать эту окружность на комплексной плоскости — взять z=exp(2 \pi i x), — то получающееся отображение это просто z->z^2. Но туда мы не пойдём...)
Victor Kleptsyn
М
18:52
Математические байки
Так вот — давайте разобьём отрезок на две части, I_0=[0,1/2) и I_1=[1/2,1). И сопоставим точке x последовательность нулей и единиц: на n-м месте поставим то, в какой интервал попадает F^n(x).
Victor Kleptsyn
М
18:52
Математические байки
Если в I_0, то 0, если в I_1, то 1.
Victor Kleptsyn
М
19:09
Математические байки
Совершенно общее утверждение при таком подходе: одно применение F приводит к сдвигу кодирующей последовательности на один символ влево.
Victor Kleptsyn
М
19:10
Математические байки
А в нашем случае всё ещё лучше:
- кодирование точки x это её двоичная запись
- если выбрать точку x равномерно на [0,1], то символы из кодирующей последовательности получаются как подбрасывания независимых честных монеток
- кодирование точки x это её двоичная запись
- если выбрать точку x равномерно на [0,1], то символы из кодирующей последовательности получаются как подбрасывания независимых честных монеток
Victor Kleptsyn
М
19:14
Математические байки
А, например, выпадение 0,1,0 на n,n+1,n+2-ых подбрасываниях превращается в "F^n(x) между точками с двоичными записями {0,010}_2 и {0,011}_2 — то есть на полуинтервале [1/4, 3/8)".
Victor Kleptsyn
М
19:16
Математические байки
Соответственно, игра Penney превращается в размещение "лунок": сначала один, потом второй игрок размещают лунки-отрезки длиной по 1/2^k; начальная точка выбирается равномерно случайно, и итерируется отображением F. В чью лунку она попадёт первой, тот победил.
Victor Kleptsyn
М
19:18
Математические байки
Бунимович, правда, использовал немного другое отображение, "tent map" — F(x)=|2x-1|.
Victor Kleptsyn
М
19:19
Математические байки
Но кодирование к этому отображению можно применить совершенно так же, просто дословно с теми же I_0 и I_1.
Victor Kleptsyn
М
19:21
Математические байки
И он больше говорил о вопросе "какова мера начальных условий, которые не попадают в одну лунку J за время n" (она убывает экспоненциально с ростом n, но по-разному для разных лунок одинаковой длины).
Victor Kleptsyn
М
19:22
Математические байки
Но на этом месте я, пожалуй, прекращу дозволенные речи. :)
Victor Kleptsyn
16 August 2019
М
12:13
Математические байки
В Bedlewo сегодня завершается конференция "2020 Vision for the dynamics" (https://www.impan.pl/en/activities/banach-center/conferences/19-vision2020 ), посвящённая памяти А. Б. Катка (https://ru.wikipedia.org/wiki/Каток,_Анатолий_Борисович ). И мне хотелось поделиться ещё парой фотографий с докладов:
Victor Kleptsyn
М
12:13
Математические байки
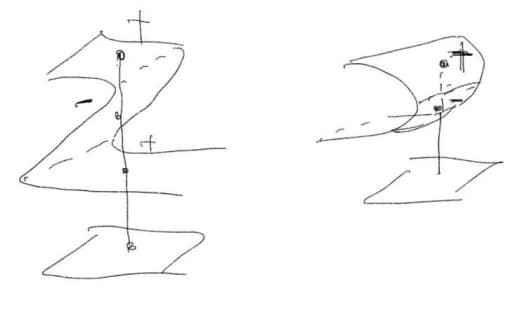
С доклада Е. А. Робинсона-младшего (https://blogs.gwu.edu/robinson/ ) :
Victor Kleptsyn
М
12:16
Математические байки
Как раз та самая подстановка Фибоначчи, о которой в Дубне рассказывал А. П. Веселов: ( https://vk.com/videos-65937233?z=video-65937233_456239054%2Fclub65937233%2Fpl_-65937233_-2 / https://mccme.ru/dubna/2019/courses/veselov.html )
Victor Kleptsyn
М
12:20
Математические байки
Из той же лекции — мозаика Пенроуза: не периодичная, но квазипериодичная (любой кусочек, который появляется хоть где-то, появляется везде — по кусочку можно назвать такой радиус R, что копия кусочка есть внутри любого круга радиуса R).
Victor Kleptsyn
М
12:23
Математические байки
А вот эта — из лекции Марка Полликотта (https://warwick.ac.uk/fac/sci/maths/people/staff/mark_pollicott/p1/ ) —
Victor Kleptsyn
М
12:24
Математические байки
На фотографии можно узнать аффинное динамически определённое канторово множество. И, конечно, простейший пример — стандартное КМ:
Victor Kleptsyn
М
12:34
Математические байки
Вопрос тут был вполне естественный — но я расскажу сначала его упрощённую версию.
Можно спрашивать, как себя ведут типичные точки отрезка. Но тут ответ простой — если считать 0 и 1 в двоичной записи случайной точки отрезка, то для типичной точки их будет примерно поровну.
А можно спросить, какая размерность множества тех точек, у которых доля единиц в первых n цифрах стремится к заданному p, 0<p<1. И как эта размерность зависит от p.
Можно спрашивать, как себя ведут типичные точки отрезка. Но тут ответ простой — если считать 0 и 1 в двоичной записи случайной точки отрезка, то для типичной точки их будет примерно поровну.
А можно спросить, какая размерность множества тех точек, у которых доля единиц в первых n цифрах стремится к заданному p, 0<p<1. И как эта размерность зависит от p.
Victor Kleptsyn
М
12:36
Математические байки
Конечно, сразу возникает вопрос, что такое "размерность" — и если отвечать строго, то нужно сказать, что это _хаусдорфова размерность_:
если есть покрытие множества X (бесконечным) объединением шаров радиусов r_j, то его d-мерным объёмом называется сумма ряда из (r_j)^d.
Хаусдорфова размерность множества — инфимум таких d, для которых существуют покрытия со сколь угодно малым d-мерным объёмом.
если есть покрытие множества X (бесконечным) объединением шаров радиусов r_j, то его d-мерным объёмом называется сумма ряда из (r_j)^d.
Хаусдорфова размерность множества — инфимум таких d, для которых существуют покрытия со сколь угодно малым d-мерным объёмом.
Victor Kleptsyn
М
12:37
Математические байки
(Пара слов об этом написана в конце дубнинской брошюры Ильяшенко — https://www.mccme.ru/dubna/books/pdf/ilyashenko-attr.pdf )
Victor Kleptsyn
М
12:41
Математические байки
Но можно пока о строгом определении не задумываться и подменить вопрос: зафиксировать большое n и посмотреть на те точки, у которых среди первых n цифр доля единиц уже (примерно) p. Например, у которых единиц ровно m=[pn].
Это будет объединение скольки-то отрезков длины 2^(-n) — если мы совсем зафиксировали число единиц, то их количество это биномиальный коэффициент C_n^m.
Это будет объединение скольки-то отрезков длины 2^(-n) — если мы совсем зафиксировали число единиц, то их количество это биномиальный коэффициент C_n^m.
Victor Kleptsyn
М
12:44
Математические байки
Соответственно, если мы думаем в терминах размерности — то правильно посмотреть, как какая степень от размера растёт количество этих отрезков. (Отрезок покрывается сотней отрезков длины 1/100, квадрат — 100^2 квадратов со стороной 1/100, d-мерный куб — 100^d кубиками со стороной 1/100.)
Victor Kleptsyn
М
12:45
Математические байки
То есть нужно посмотреть на отношение
log_2 (C_n^m) / n
log_2 (C_n^m) / n
Victor Kleptsyn
М
12:47
Математические байки
Формула Стирлинга (потрясающе полезная, которую надо помнить обязательно) говорит, что
n! ~ \sqrt{2 \pi n} (n/e)^n.
n! ~ \sqrt{2 \pi n} (n/e)^n.
Victor Kleptsyn
М
13:05
Математические байки
Нам тут понадобится только последний сомножитель, экспоненциальный (всё остальное слишком медленное относительно логарифма). Ну и в выражении
C_n^m = n!/(m! (n-m)!)
степени e в числителе и знаменателе сокращаются, и остаётся от экспоненциальной части только
(n/m)^m (n/(n-m))^(n-m).
C_n^m = n!/(m! (n-m)!)
степени e в числителе и знаменателе сокращаются, и остаётся от экспоненциальной части только
(n/m)^m (n/(n-m))^(n-m).
Victor Kleptsyn
М
13:06
Математические байки
Если прологарифмировать, поделить на n и сказать, что m~np, то получается примерно
(1/n) log_2 C_n^m ~ -p log_2 p - (1-p) log_2 (1-p).
(1/n) log_2 C_n^m ~ -p log_2 p - (1-p) log_2 (1-p).
Victor Kleptsyn
М
13:07
Математические байки
С одной стороны, вот она размерность. Мы её и правда нашли (хотя, конечно, всё вышесказанное нужно делать честно, а не как я сейчас).
Victor Kleptsyn
М
13:13
Математические байки
И этим занимался Безикович — тот самый, который решил задачу Какейя о развороте отрезка: что есть (невыпуклая) фигура сколь угодно малой площади, внутри которой можно развернуть отрезок.
Victor Kleptsyn
М
13:16
Математические байки
(У Марка на слайде в знаменателе логарифм 3, а не логарифм 2 — потому что он вместо отрезка работает с канторовым множеством: его точки тоже можно закодировать 0 и 1, или 0 и 2 — просто взяв троичную запись.)
Victor Kleptsyn
М
13:19
Математические байки
In reply to this message
(Да, в качестве отступления в сторону — об этой задаче и конструкции можно прочитать в Кванте —
http://kvant.mccme.ru/1973/04/o_vrashchenii_otrezka.htm )
http://kvant.mccme.ru/1973/04/o_vrashchenii_otrezka.htm )
Victor Kleptsyn
М
13:20
Математические байки
In reply to this message
Так вот — с другой стороны, тут появляется выражение (-p log p), которое кому-то может быть знакомо из физики, а кому-то из информатики.
Victor Kleptsyn
М
13:34
Математические байки
И мне в этом месте хочется сказать слова "энтропия Шеннона".
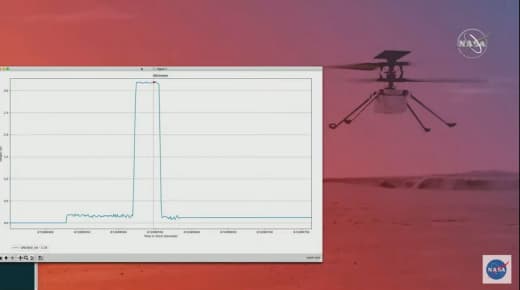
Представим себе, что на Марсе у нас стоит марсоход, и каждую секунду что-то измеряет. Например, ловит космические лучи — таким образом, разные измерения независимы друг от друга. Но шанс, что что-то прилетит, очень маленький, поэтому таблица из 0 и 1 (не прилетело/прилетело) состоит в основном из нулей, вероятность p единицы очень маленькая.
Как нам передать результаты наблюдений на Землю?
Представим себе, что на Марсе у нас стоит марсоход, и каждую секунду что-то измеряет. Например, ловит космические лучи — таким образом, разные измерения независимы друг от друга. Но шанс, что что-то прилетит, очень маленький, поэтому таблица из 0 и 1 (не прилетело/прилетело) состоит в основном из нулей, вероятность p единицы очень маленькая.
Как нам передать результаты наблюдений на Землю?
Victor Kleptsyn
М
13:35
Математические байки
Можно, конечно, так и передать, нулями и единицами, но странно забивать канал нулями.
Victor Kleptsyn
М
13:37
Математические байки
Так вот — при большом числе наблюдений нам понадобится примерно (-p log p - (1-p) log (1-p)) бит в расчёте на одно измерение, чтобы (честно) передать результаты.
Victor Kleptsyn
М
13:39
Математические байки
Проще всего это сделать так — если мы провели n измерений, то сначала передаём m — число единиц. На это нам нужно log_2(n) бит, что по сравнению с n — копейки.
Victor Kleptsyn
М
13:43
Математические байки
Теперь, когда мы знаем число единиц — у нас есть C_n^m разных вариантов, и на самом деле, они все равновероятны. Поэтому понятно, что меньше, чем log_2 (C_n^m) битами, мы не обойдёмся. А чтобы передать за это число бит — например, можно (мысленно) лексикографически упорядочить все C_n^m последовательностей из m единиц и (n-m) нулей, и заметить, что соответствие между номером последовательности и самой последовательностью несложно вычисляется в обе стороны.
Victor Kleptsyn
М
13:43
Математические байки
Остаётся передать номер — что мы и сделаем.
Victor Kleptsyn
18 August 2019
М
12:46
Математические байки
Чтобы закончить позавчерашнюю байку — если у нас в эксперименте будут не 0 и 1, а несколько разных исходов 1,...,k — все со своими вероятностями p_1,...,p_k, — то вместо биномиального коэффициента будет мультиномиальный, из n по набору (m_1,...,m_k) того, сколько раз какой исход выпал.
Victor Kleptsyn
М
12:46
Математические байки
То есть
n!/((m_1)!*...*(m_k)!)
n!/((m_1)!*...*(m_k)!)
Victor Kleptsyn
М
12:48
Математические байки
Опять применив формулу Стирлинга и посмотрев на экспоненциальную часть, мы получим произведение (n/m_i)^(m_i), и его логарифм будет равен
n * (-\sum p_i log p_i).
n * (-\sum p_i log p_i).
Victor Kleptsyn
М
12:48
Математические байки
Вот мы и получили знаменитую формулу для энтропии — число бит для передачи результата в расчёте на один эксперимент (или, по-другому, какая пропускная способность канала нам нужна):
H = - \sum_i p_i \log p_i.
H = - \sum_i p_i \log p_i.
Victor Kleptsyn
М
12:49
Математические байки
Для аккуратности — если говорить о битах, то логарифм нужно брать двоичным, а в динамических системах и в физике его обычно берут натуральным.
Victor Kleptsyn
М
12:50
Математические байки
In reply to this message
Ещё на эту формулу можно посмотреть так: это математическое ожидание ( = результат усреднения) логарифма вероятности того исхода, которое у нас в результате одного эксперимента получается.
Victor Kleptsyn
М
12:54
Математические байки
Так что можно сказать, что логарифм вероятности пронаблюдённого (случившегося) исхода — это та информация, которую мы в результате эксперимента получаем.
Victor Kleptsyn
М
12:55
Математические байки
В какой-то из популярных книжек (ещё времён, когда телефоны были проводными) мне попадалось сравнение
"Если Вы снимете трубку звонящего телефона и услышите "Алло!", Вы не удивитесь. Гораздо больше Вы удивитесь, если Вас вместо этого ударит током."
"Если Вы снимете трубку звонящего телефона и услышите "Алло!", Вы не удивитесь. Гораздо больше Вы удивитесь, если Вас вместо этого ударит током."
Victor Kleptsyn
М
14:31
Математические байки
In reply to this message
==
Ну и возвращаясь к докладу Марка Полликотта (а то я про Безиковича и долю единиц рассказал, а про центральный сюжет ещё нет).
Ну и возвращаясь к докладу Марка Полликотта (а то я про Безиковича и долю единиц рассказал, а про центральный сюжет ещё нет).
Victor Kleptsyn
М
14:31
Математические байки
Там тоже обсуждалась хаусдорфова размерность, но не точек с данной долей 0 и 1, а точек с данной скоростью растяжения для того отображения T, которое канторово множество порождает.
Victor Kleptsyn
М
14:32
Математические байки
По-хорошему, про скорость растяжения произносятся слова "показатель Ляпунова" (которые для современной теории динамических систем одни из основных).
Victor Kleptsyn
М
14:32
Математические байки
А именно — это предел
lim_n (1/n) ln (T^n)'(x):
lim_n (1/n) ln (T^n)'(x):
Victor Kleptsyn
М
14:34
Математические байки
Чуть более подробно — вот пусть у нас есть динамическая система, то есть отображение T, которое мы итерируем (можно сказать, что оно сопоставляет текущему состоянию системы её состояние через одну секунду).
Victor Kleptsyn
М
14:35
Математические байки
И пусть задана начальное состояние системы — некоторая точка x.
Victor Kleptsyn
М
14:35
Математические байки
Тогда можно посмотреть, с какой скоростью итерации "соседних" с ней точек с её итерациями сближаются/разбегаются.
Victor Kleptsyn
М
14:37
Математические байки
В размерности один — а мы будем считать, что мы работаем на отрезке, — это просто значит, что мы берём производную n-й итерации T^n в точке x:
Victor Kleptsyn
М
14:37
Математические байки
(T^n)'(x) = T'(T^{n-1}(x)) * ... * T'(T(x)) * T'(x).
Victor Kleptsyn
М
14:37
Математические байки
Теперь, чтобы сказать, "какое изменение приходится [в среднем] на одну итерацию", можно было бы извлечь корень n-й степени.
Victor Kleptsyn
М
14:38
Математические байки
Но с корнями и произведениями очень неудобно работать. Поэтому от такого "среднего геометрического производных по орбите" берут логарифм — рассматривают
(1/n) log (T^n)'(x) = (1/n) \sum_{j=0}^{n-1} (log T')(T^j(x)).
(1/n) log (T^n)'(x) = (1/n) \sum_{j=0}^{n-1} (log T')(T^j(x)).
Victor Kleptsyn
М
14:39
Математические байки
(Да, "орбита" — это как раз последовательность итераций начальной точки: x, T(x), T^2(x), ...)
Victor Kleptsyn
М
14:40
Математические байки
In reply to this message
И переходят к пределу при n, стремящемся к бесконечности. Вот этот предел (который появляется на слайде выше) и называется показателем Ляпунова (отображения T в точке x).
Victor Kleptsyn
М
14:40
Математические байки
В том случае, когда отображение T — кусочно-аффинное, порождающее канторово множество, производная у него на каждом отрезке области определения постоянна. Так что получается действительно почти "доля единиц" в кодировании точки, только чуть-чуть подкрученная.
Victor Kleptsyn
М
14:42
Математические байки
Скажем, для самого стандартного канторова множества показатель Ляпунова будет просто log 3 в любой точке x, потому что производная T равна 3 везде. А вот если у нас два отрезка, [0,1/a] и [1-1/b,1], то у нас будет
(log a)*(доля итераций, попадающих в первый отрезок) + (log b)*(доля итераций, попадающих во второй).
(log a)*(доля итераций, попадающих в первый отрезок) + (log b)*(доля итераций, попадающих во второй).
Victor Kleptsyn
М
14:43
Математические байки
(Я не хочу лезть в более конкретные детали или писать формулы; в конце концов, это должна быть сложная, но всё-таки байка!)
Victor Kleptsyn
М
14:44
Математические байки
Так вот, из общей логики "есть естественный объект, давайте его исследовать" — можно смотреть на то, как устроено множество точек с заданным показателем Ляпунова. В частности, можно спросить, какая у него размерность. И как устроена функция "размерность в зависимости от показателя Ляпунова".
Victor Kleptsyn
М
14:47
Математические байки
Эту функцию исследовал Howie Weiss. Он доказал (в определённых условиях, которые я не формулирую!) её аналитичность — и сказал, что она должна быть выпуклой.
Victor Kleptsyn
М
14:48
Математические байки
Только вот выпуклость оказалась неправдой: J. Kiwi и G. Iommi нашли контрпример.
Victor Kleptsyn
М
14:48
Математические байки
In reply to this message
Оказалось, что достаточно взять кусочно-аффинное растягивающее отображение из двух интервалов.
Victor Kleptsyn
М
14:52
Математические байки
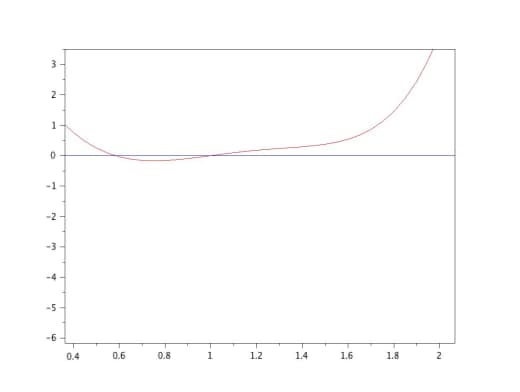
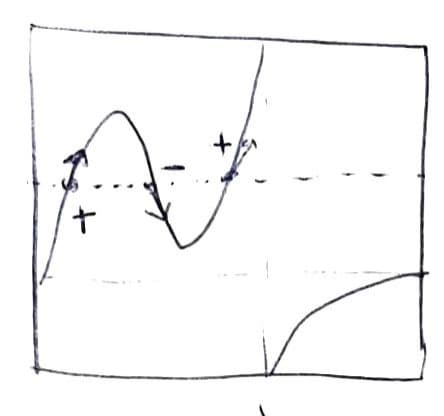
И если длины кусочков сильно разные (если отношение их логарифмов большое) — то функция уже не выпуклая:
Victor Kleptsyn
М
14:54
Математические байки
Ну и следующий вопрос — хорошо, выпуклой функция не будет, вот пример. А насколько плохой она может быть, может ли у неё быть много точек перегиба?
Victor Kleptsyn
М
14:55
Математические байки
Ответ: свежая теорема Оливера Дженкинсона, Марка Полликотта и Полины Вытновой, которой Марк завершил доклад, говорит, что точек перегиба действительно может быть сколь угодно много.
Victor Kleptsyn
М
15:11
Математические байки
Только аффинно-растягивающихся кусочков нужно брать уже не два, а сильно больше.
Victor Kleptsyn
М
15:11
Математические байки
Да, а название для таких отображений — cookie cutters, "формочки для печенья" — придумал замечательный математик Дэннис Салливан ( https://ru.wikipedia.org/wiki/Салливан,_Деннис )
Victor Kleptsyn
М
15:12
Математические байки
Ну и на этом месте, кажется, эту байку правильно завершить.
Victor Kleptsyn
М
17:56
Математические байки
===
Поскольку рассказ выше получился явно сложным — в дополнение к нему, байка о формуле Стирлинга (раз уж я её упомянул) и формуле суммирования Эйлера-Маклорена. Точнее, начало байки (ибо там рассказывать можно много).
Поскольку рассказ выше получился явно сложным — в дополнение к нему, байка о формуле Стирлинга (раз уж я её упомянул) и формуле суммирования Эйлера-Маклорена. Точнее, начало байки (ибо там рассказывать можно много).
Victor Kleptsyn
М
17:56
Математические байки
Вот у нас есть n!. Это произведение 1*2*...*n.
Victor Kleptsyn
М
17:57
Математические байки
Формула Стирлинга его оценивает — причём делает это асимптотически точно, отношение n! к \sqrt{2\pi n}*(n/e)^n стремится к 1 с ростом n.
Victor Kleptsyn
М
17:57
Математические байки
Как такую оценку можно получить?
Victor Kleptsyn
М
17:58
Математические байки
Есть очень хороший рефлекс: "видишь длинное произведение — прологарифмируй!".
Victor Kleptsyn
М
17:58
Математические байки
Потому что логарифм превращает произведение в сумму, а с суммой работать значительно проще.
Victor Kleptsyn
М
17:58
Математические байки
Применив его — мы видим, что мы хотим понять, как себя ведёт
ln n! = ln 1 + ln 2 + ... + ln n.
ln n! = ln 1 + ln 2 + ... + ln n.
Victor Kleptsyn
М
17:59
Математические байки
И уже сразу видно, что она напоминает интегральную сумму Римана для интеграла от логарифма:
Victor Kleptsyn
М
18:03
Математические байки
А какая у логарифма первообразная? Поскольку логарифм меняется чем дальше, тем медленнее, естественно взять x*(ln x) в качестве первого приближения; но
[x*(ln x)]'= ln x + x*[(ln x)'] = ln x +1,
так что нужно первообразную лишней единицы вычесть — получается (x*ln x -x)
[x*(ln x)]'= ln x + x*[(ln x)'] = ln x +1,
так что нужно первообразную лишней единицы вычесть — получается (x*ln x -x)
Victor Kleptsyn
М
18:04
Математические байки
(Конечно, это называется "взять интеграл по частям", но тут эта выкладка ещё и естественно мотивируется.)
Victor Kleptsyn
М
18:10
Математические байки
А (n*ln n -n) — это и есть логарифм от "экспоненциальной части" (n/e)^n.
То есть первую часть формулы Стирлинга мы уже поймали!
То есть первую часть формулы Стирлинга мы уже поймали!
Victor Kleptsyn
М
18:12
Математические байки
In reply to this message
На самом деле — удобнее откладывать прямоугольники в другую сторону, чтобы интеграл был действительно до x=n, то есть чтобы ln k был площадью прямоугольника высоты ln k на основании [k-1,k], тогда картинка получится чуть-чуть другая:
Victor Kleptsyn
М
18:13
Математические байки
Закрашенная область — то, что мы хотим получить. А площадь под (красным) графиком логарифма — то, что уже посчитали.
Victor Kleptsyn
М
18:13
Математические байки
А насколько мы промахнулись?
Victor Kleptsyn
М
18:17
Математические байки
Понятно, насколько — на сумму площадей криволинейных треугольников:
Victor Kleptsyn
М
18:17
Математические байки
А чему она примерно равна?
Victor Kleptsyn
М
18:18
Математические байки
Естественно, сумме площадей таких же, но прямолинейных треугольников.
Victor Kleptsyn
М
18:19
Математические байки
У всех этих прямолинейных треугольников горизонтальные катеты равны 1. Поэтому сумма их площадей это половина суммы вертикальных катетов.
Victor Kleptsyn
М
18:20
Математические байки
А поскольку каждый катет это приращение логарифма — то сумма вертикальных катетов получается телескопическая, и даёт просто ln n.
Victor Kleptsyn
М
18:21
Математические байки
Ну и (ln n)/2 — это не что иное, как логарифм корня из n. Того самого корня из n, который стоит в формуле Стирлинга.
Victor Kleptsyn
М
18:22
Математические байки
(Да, на всякий случай — то, что мы сейчас проделали, для численных приближений интеграла называлось бы переходом от формулы прямоугольников к формуле трапеций.)
Victor Kleptsyn
М
18:23
Математические байки
Так вот — мы сейчас вытащили почти всю формулу Стирлинга, кроме константы \sqrt{2\pi}.
Victor Kleptsyn
М
18:25
Математические байки
На самом деле — мы уже можем доказать, что эта константа _есть_.
Victor Kleptsyn
М
18:27
Математические байки
Для этого заметим, что ошибка, которую мы оставили после учёта прямолинейных треугольников, складывается из площадей сегментов — между хордой и графиком логарифма.
Victor Kleptsyn
М
18:30
Математические байки
Если площадь криволинейного треугольника убывала как (1/n) — ибо за него отвечает первая производная логарифма — то площадь сегмента уже будет убывать как (1/n^2), ибо ему соответствует вторая производная, а (ln x)'' = -1/x^2.
Victor Kleptsyn
М
18:32
Математические байки
А ряд из обратных квадратов уже сходится. И значит, последовательность "ошибок"
(ln n!) - ( n ln n - n + ln \sqrt{n})
будет фундаментальной — её приращения и есть площади сегментов.
(ln n!) - ( n ln n - n + ln \sqrt{n})
будет фундаментальной — её приращения и есть площади сегментов.
Victor Kleptsyn
М
18:34
Математические байки
А раз так, то она сходится — и её предел это и есть логарифм той константы, на которую нам остаётся домножить.
Victor Kleptsyn
М
18:35
Математические байки
То есть для какого-то A будет выполнено
ln n! ~ A sqrt{n} (n/e)^n,
только мы пока что не знаем, что A= \sqrt{2\pi}.
ln n! ~ A sqrt{n} (n/e)^n,
только мы пока что не знаем, что A= \sqrt{2\pi}.
Victor Kleptsyn
М
18:46
Математические байки
На самом деле, техника, которую мы сейчас применили, это частный случай формулы суммирования Эйлера-Маклорена. А именно — если у нас есть какая-то "хорошая" функция f, и мы хотим понять, как себя будет вести сумма
f(1)+f(2)+...+f(n)
с ростом n.
f(1)+f(2)+...+f(n)
с ростом n.
Victor Kleptsyn
М
18:49
Математические байки
Если провести всё те же рассуждения (и зайти чуть дальше) — то в качестве первого приближения возникнет первообразная F(n), потом к ней добавится (1/2)*f(n), потом с каким-то коэффициентом добавится производная f', и так далее.
Victor Kleptsyn
М
18:55
Математические байки
Причём коэффициенты не зависят от того, у какой именно функции f мы складываем значения, мы всегда получим выражение вида
F(n)+ (1/2) f(n) + (1/12) f'(n) + ... .
F(n)+ (1/2) f(n) + (1/12) f'(n) + ... .
Victor Kleptsyn
М
18:57
Математические байки
Если очередная производная f начинает убывать достаточно быстро, чтобы ряд из поправок начал сходиться — можно сказать, что сумма будет устроена как приближение плюс неизвестная нам константа.
Victor Kleptsyn
М
19:01
Математические байки
Но асимптотику можно писать и дальше — собственно, ровно так получается приближение для суммы гармонического ряда,
1+(1/2)+...+(1/n) = ln n + \gamma + (1/2)* (1/n) + o(1/n),
где \gamma — постоянная Эйлера.
1+(1/2)+...+(1/n) = ln n + \gamma + (1/2)* (1/n) + o(1/n),
где \gamma — постоянная Эйлера.
Victor Kleptsyn
М
19:05
Математические байки
И ровно поэтому в формуле Стирлинга, если n! нужно приблизить ещё точнее, нужно домножить правую часть на exp(1/12n) — или на (1+ 1/12n), с точностью до O(1/n^2) это одно и то же. Потому что вот он коэффициент (1/12) для производной, и вот она производная логарифма, (ln x)'=1/x.
Victor Kleptsyn
М
19:06
Математические байки
А ещё очень естественное действие — применить всё это к самым простым функциям, которые бывают, к степеням.
Victor Kleptsyn
М
19:10
Математические байки
И получится сумма степеней — которую для небольших степеней все видели; скажем, для суммы первых степеней —
1+2+...+n=n(n+1)/2 = n^2/2 + n/2 = F(n) + (1/2) f(n).
1+2+...+n=n(n+1)/2 = n^2/2 + n/2 = F(n) + (1/2) f(n).
Victor Kleptsyn
М
19:15
Математические байки
Для суммы квадратов — есть формула n(n+1)(2n+1)/6, а если раскрыть скобки, получится
n^3/3 + n^2/2 + n/6 = F(n) + (1/2)f(n) + (1/12)f'(n)
n^3/3 + n^2/2 + n/6 = F(n) + (1/2)f(n) + (1/12)f'(n)
Victor Kleptsyn
М
19:24
Математические байки
Вообще про суммы степеней есть очень хороший текст Г. Мерзона в "Мат. просвещении" — http://mi.mathnet.ru/mp882 —
а мне хочется сказать ещё пару слов про сумму _обратных_ степеней.
а мне хочется сказать ещё пару слов про сумму _обратных_ степеней.
Victor Kleptsyn
М
19:28
Математические байки
Была знаменитая базельская проблема — найти, чему равна сумма ряда из обратных квадратов,
1+1/4+1/9+...
1+1/4+1/9+...
Victor Kleptsyn
М
19:28
Математические байки
Её решил Эйлер, найдя известный сейчас ответ \pi^2/6
Victor Kleptsyn
М
19:31
Математические байки
И работая над этой задачей — он сначала вычислил эту сумму с огромной точностью — у него было шесть верных десятичных знаков.
Victor Kleptsyn
М
19:37
Математические байки
И можно сразу понять, что "напрямую" это сделать не получилось бы. Потому что сумма "хвоста" ряда из обратных квадратов убывает как (1/n). То есть, чтобы добыть эти шесть верных знаков, надо было бы просуммировать миллион слагаемых — вручную!
Victor Kleptsyn
М
19:39
Математические байки
Но — если мы уже знаем, насколько промахнёмся, то почему бы не исправить эту ошибку?
Victor Kleptsyn
М
19:40
Математические байки
Почему бы не сказать, что отбросив "хвост", сумму 1/m^2 при m>=n, мы примерно промахнёмся на первообразную от 1/x^2?
Victor Kleptsyn
М
19:41
Математические байки
А потом поправить это приближение, учтя, насколько 1/m^2 отличается от интеграла от 1/x^2 на отрезке [m,m+1].
Victor Kleptsyn
М
19:44
Математические байки
И это, конечно, та же самая техника, что мы видели выше.
Victor Kleptsyn
М
19:46
Математические байки
Уже если учесть только (1/n) как первое приближение для суммы
f(n+1)+f(n+2)+...,
где f(x)=1/x^2,
то мы получим для суммы всего ряда приближение
f(1)+...+f(n)+1/n,
с ошибкой, убывающей, как (1/n^2).
f(n+1)+f(n+2)+...,
где f(x)=1/x^2,
то мы получим для суммы всего ряда приближение
f(1)+...+f(n)+1/n,
с ошибкой, убывающей, как (1/n^2).
Victor Kleptsyn
М
19:49
Математические байки
Если перейти к формуле треугольников — ошибка будет убывать как (1/n^3), и шесть знаков уже становятся достижимы: теперь хватит n=100. (Не думаю, что сложение сотни дробей вручную может кого-то воодушевить, но по крайней мере, задача перешла из категории "невозможно" в категорию "муторно, но если очень надо..."). А можно ведь учесть ещё пару производных...
Victor Kleptsyn
М
19:58
Математические байки
Насколько я понимаю, Эйлер действовал _не_ так. Он (я тут ссылаюсь на книгу W. Dunham, "Euler: The Master of Us All" — по-хорошему, надо было бы поднять первоисточники, но я этого ещё не сделал) красивым интегрированием выяснил, что вместо просто суммы обратных квадратов можно взять сумму ряда
\sum_n 1/(n^2 * 2^(n-1)) —
и добавить к нему (ln 2)^2.
\sum_n 1/(n^2 * 2^(n-1)) —
и добавить к нему (ln 2)^2.
Victor Kleptsyn
М
20:04
Математические байки
И поскольку у нового ряда слагаемые убывают с экспоненциальной скоростью, посчитать его сумму с нужным числом знаков можно было из совсем небольшого количества слагаемых.
Victor Kleptsyn
М
20:04
Математические байки
Что Эйлер и сделал.
Victor Kleptsyn
М
20:07
Математические байки
Но — для этого нужно было придумать тот ход с интегрированием. И для этого тогда надо было быть Эйлером.
Victor Kleptsyn
М
20:07
Математические байки
А мне хотелось правильным показать, что с помощью подхода выше ("ошибаемся — давайте посмотрим, на сколько, и учтём") задача [численного] вычисления тоже делалась.
Victor Kleptsyn
М
20:08
Математические байки
С большими трудозатратами, быть может, но — делалась, а не стояла непреодолимой стеной.
Victor Kleptsyn
М
20:09
Математические байки
И это, кажется, хороший момент на сегодня прекратить дозволенные речи.
Victor Kleptsyn
24 August 2019
М
15:59
Математические байки
Продолжим, пожалуй?
Victor Kleptsyn
М
15:59
Математические байки
В прошлый раз мы закончили с формулой Стирлинга на том, что n!~A \sqrt{n} (n/e)^n — но мы ещё не знаем, что A это корень из 2π.
Victor Kleptsyn
М
15:59
Математические байки
Так вот — оказывается, что корень из 2π, который в формуле Стирлинга в числителе, это "тот же самый" корень из 2π, который у нормального распределения (того, что появляется в центральной предельной теореме) в знаменателе. И есть два способа это увидеть.
Victor Kleptsyn
М
16:00
Математические байки
Первый — это заодно и способ саму центральную предельную теорему в простейшем случае увидеть.
Victor Kleptsyn
М
16:00
Математические байки
А именно, давайте зададимся вполне естественным вопросом: если мы подкидываем честную монетку N=2n раз, какие результаты мы будем наблюдать, и с какой вероятностью?
Victor Kleptsyn
М
16:00
Математические байки
Понятно, что наиболее вероятный результат это n орлов и n решек: вероятность из N подбрасываний выкинуть M орлов равна C_N^M / 2^N, а "центральный" биномиальный коэффициент C_{2n}^n самый большой.
А как такая вероятность начинает уменьшаться?
А как такая вероятность начинает уменьшаться?
Victor Kleptsyn
М
16:01
Математические байки
Скажем, при 10000 подбрасываний — какие количества орлов естественны, а какие неправдоподобны и должны заставить заподозрить, что монетка гнутая (или ещё что-нибудь не так)?
5025? 5320? 6500?
5025? 5320? 6500?
Victor Kleptsyn
М
16:02
Математические байки
Давайте заметим, что
(C_N^{a+1}) / (C_N^a) = (N-a)/(a+1).
Потому что если в классе из N человек уже выбрано a дежурных, то есть N-a вариантов, как можно назначить (a+1)-го — и каждый набор из (a+1) дежурного получается (a+1) способами.
(C_N^{a+1}) / (C_N^a) = (N-a)/(a+1).
Потому что если в классе из N человек уже выбрано a дежурных, то есть N-a вариантов, как можно назначить (a+1)-го — и каждый набор из (a+1) дежурного получается (a+1) способами.
Victor Kleptsyn
М
16:02
Математические байки
Сравним теперь C_{2n}^n и C_{2n}^{n+k}: второй отличается от первого умножением на
n/(n+1) * (n-1)/(n+2) * ... * (n-k+1)/(n+k).
n/(n+1) * (n-1)/(n+2) * ... * (n-k+1)/(n+k).
Victor Kleptsyn
М
М
16:03
Математические байки
Получилось произведение k сомножителей.
А как я уже говорил, "видишь длинное произведение — прологарифмируй!"
А как я уже говорил, "видишь длинное произведение — прологарифмируй!"
Victor Kleptsyn
М
16:04
Математические байки
Логарифм отношения этих биномиальных коэффициентов равен сумме логарифмов
ln (1- (2j-1)/(n+j) )
по j от 1 до k.
ln (1- (2j-1)/(n+j) )
по j от 1 до k.
Victor Kleptsyn
М
16:04
Математические байки
А ln(1+x) примерно равен x. Поэтому будет сумма от
-(2j-1)/(n+j);
да ещё и, если k<<n, то знаменатель можно заменить просто на n. И получается сумма от (2j-1)/n, а сумма нечётных чисел от 1 до (2k-1) это k^2:
-(2j-1)/(n+j);
да ещё и, если k<<n, то знаменатель можно заменить просто на n. И получается сумма от (2j-1)/n, а сумма нечётных чисел от 1 до (2k-1) это k^2:
Victor Kleptsyn
М
16:05
Математические байки
То есть вероятность отклонения на k падает со скоростью e^{-k^2/n}.
Victor Kleptsyn
М
16:06
Математические байки
В частности, характерные отклонения имеют порядок корня из n — и слишком большие отклонения даже такого порядка мы в жизни никогда не увидим (ибо, например, e^{-25}<10^{-10})
Victor Kleptsyn
М
М
М
16:08
Математические байки
Хорошо, а всё-таки — при чём тут формула Стирлинга?
Victor Kleptsyn
М
16:09
Математические байки
Давайте её применим, чтобы оценить C_{2n}^n.
Неизвестный нам коэффициент A вылезет один раз в числителе — и два раза в знаменателе, так что не сократится:
Неизвестный нам коэффициент A вылезет один раз в числителе — и два раза в знаменателе, так что не сократится:
Victor Kleptsyn
М
М
16:11
Математические байки
Соответственно, вероятность получить в 2n подбрасываниях (n+k) орлов примерно равна
Victor Kleptsyn
М
М
16:11
Математические байки
А чему равна сумма всех таких вероятностей?
Victor Kleptsyn
М
16:12
Математические байки
С одной стороны, сумма вероятностей равна единице (ну или сумма биномиальных коэффициентов — соответствующей степени двойки).
Victor Kleptsyn
М
16:12
Математические байки
С другой, сумма правых частей, если обозначить x_k = k/\sqrt{n}, оказывается интегральной суммой Римана для интеграла от e^{-x^2}:
Victor Kleptsyn
М
М
16:13
Математические байки
И стремится с ростом n она к соответствующему интегралу:
Victor Kleptsyn
М
М
16:14
Математические байки
А поскольку предел должен равняться единице — мы (почти) нашли A:
Victor Kleptsyn
М
М
16:15
Математические байки
Остаётся посчитать интеграл в правой части. Как мы уже знаем из продекларированного ответа, он должен равняться корню из π.
Victor Kleptsyn
М
16:16
Математические байки
Есть такой неформальный принцип — пи может появиться только как длина окружности, всё, где оно возникает, должно быть как-то с окружностью связано. Пусть опосредованно, пусть не сразу видно — но где-то окружность должна быть закопана.
Victor Kleptsyn
М
16:16
Математические байки
Поэтому корень из пи — штука странная. Гораздо лучше возвести этот интеграл в квадрат:
Victor Kleptsyn
М
М
16:16
Математические байки
После чего увидеть, что правая часть инвариантна относительно поворотов — и вот она, _окружность_ направлений!
Victor Kleptsyn
М
16:18
Математические байки
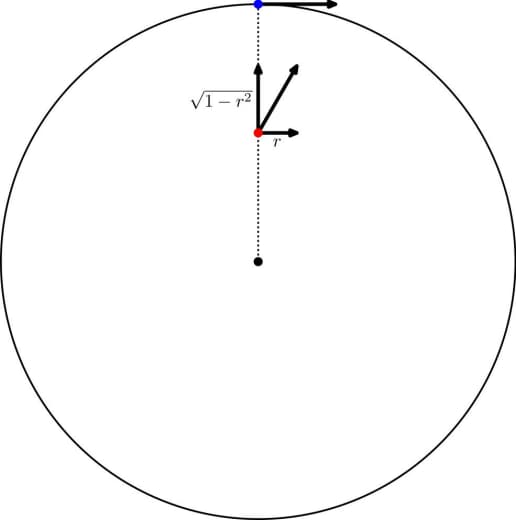
Переход в полярные координаты, или (на школьно/физическом уровне строгости) нарезание плоскости на кольца
r^2 <= x^2+y^2 < (r+dr)^2 )
легко довершит дело — и я оставлю тут это как упражнение.
r^2 <= x^2+y^2 < (r+dr)^2 )
легко довершит дело — и я оставлю тут это как упражнение.
Victor Kleptsyn
М
16:18
Математические байки
Всё, победа, точное значение A=\sqrt{2\pi} получено!
Victor Kleptsyn
М
16:18
Математические байки
Но на самом деле мы на этом пути получили больше: то, что мы только что проделали, называется предельной теоремой Муавра-Лапласа, простейшим частным случаем предельной теоремы.
Victor Kleptsyn
М
16:21
Математические байки
Хорошая анимированная иллюстрация к тому, что мы увидели —
Victor Kleptsyn
М
М
16:21
Математические байки
Victor Kleptsyn
М
16:23
Математические байки
Вообще, центральная предельная теорема утверждает вот что. Пусть если мы рассматриваем сумму большого числа "разумных" (не слишком "больших"), более-менее сравнимых и независимых случайных слагаемых (например, считая количество орлов за десять тысяч подбрасываний монетки).
Victor Kleptsyn
М
16:24
Математические байки
У такой суммы будет какое-то среднее значение; и будут отклонения от него.
Victor Kleptsyn
М
16:28
Математические байки
Среднее значение на то и среднее, чтобы в среднем отклонения "в плюс" и "в минус" были одинаковы. Но можно посмотреть на среднеквадратичное отклонение (на дисперсию, для тех, кому знакомо это слово).
Victor Kleptsyn
М
16:31
Математические байки
Так вот, давайте отклонение от среднего перемасштабируем — поделив его на его среднее квадратичное. (Каковое, при одинаково распределённых слагаемых, растёт как корень из n — что мы, собственно, и наблюдали в нашем случае.)
Victor Kleptsyn
М
16:33
Математические байки
Центральная предельная теорема утверждает, что — что бы мы ни складывали исходно, в пределе получится одно и то же, _универсальное_, распределение: гауссовское, или нормальное, распределение.
Victor Kleptsyn
М
16:34
Математические байки
Так вот — мы сейчас увидели, что для случая подбрасывания монетки шанс, что отношение k/sqrt{n} попадёт в какой-то интервал [a,b], можно приблизить как интегральную сумму Римана — которая, в свою очередь, стремится к интегралу:
Victor Kleptsyn
М
М
16:37
Математические байки
То есть в пределе тут мы видим распределение, у которого есть "линейная плотность"
1/\sqrt{\pi} * e^{-x^2}.
1/\sqrt{\pi} * e^{-x^2}.
Victor Kleptsyn
М
16:38
Математические байки
Правда, мы делили отклонение на корень из n, а если посмотреть чуть аккуратнее, то средний квадрат отклонения равен n/2, соответственно, чтобы получить совсем предел "как в ЦПТ", делить надо было на \sqrt{n/2}.
Victor Kleptsyn
М
16:38
Математические байки
Если распределение выше в корень из двух раз растянуть — получится распределение с плотностью
Victor Kleptsyn
М
М
16:39
Математические байки
И именно сходимость к распределению с такой плотностью и утверждает центральная предельная теорема.
Victor Kleptsyn
М
18:09
Математические байки
===
В рассуждениях выше уже видно, что A, которое оказывается множителем в формуле Стирлинга, появляется в знаменателе у гауссовой плотности.
Но я обещал два подхода; второй, через гамма-функцию — это одновременно и способ увидеть формулу Стирлинга непосредственно, без рассуждений с суммами логарифмов.
В рассуждениях выше уже видно, что A, которое оказывается множителем в формуле Стирлинга, появляется в знаменателе у гауссовой плотности.
Но я обещал два подхода; второй, через гамма-функцию — это одновременно и способ увидеть формулу Стирлинга непосредственно, без рассуждений с суммами логарифмов.
Victor Kleptsyn
М
18:09
Математические байки
Оказывается, факториал можно представить и интегралом:
n! = \int_0^{\infty} x^n e^{-x} dx.
n! = \int_0^{\infty} x^n e^{-x} dx.
Victor Kleptsyn
М
М
18:11
Математические байки
Собственно, интеграл в правой части называется гамма-функцией — и в него можно подставлять не только целые значения показателя у x:
Г(a) := \int_0^{\infty} x^{a-1} e^{-x} dx;
так что формула выше утверждает, что n!=Г(n+1).
Г(a) := \int_0^{\infty} x^{a-1} e^{-x} dx;
так что формула выше утверждает, что n!=Г(n+1).
Victor Kleptsyn
М
18:12
Математические байки
Интегрируя по частям, легко проверить, что Г(a+1)=a Г(a), и по индукции проверить, что действительно
Г(n+1)=n!.
Г(n+1)=n!.
Victor Kleptsyn
М
18:12
Математические байки
Так вот — а как бы нам оценить, чему равен этот интеграл?
Victor Kleptsyn
М
18:12
Математические байки
Сначала посмотрим: а где подынтегральная функция f(x)=x^n e^{-x} принимает максимальное значение?
Victor Kleptsyn
М
18:18
Математические байки
Запишем её как exp(g(x)), где
g(x)= ln f(x) = (n ln x - x);
g(x)= ln f(x) = (n ln x - x);
Victor Kleptsyn
М
18:19
Математические байки
тогда мы хотим максимизировать g(x). Её производная равна g'(x)=n/x -1, значит, максимальное значение принимается в точке x_0=n.
Victor Kleptsyn
М
18:19
Математические байки
И равно оно f(n)=(n/e)^n — то есть мы опять поймали экспоненциальную часть приближения.
Victor Kleptsyn
М
18:22
Математические байки
Вынесем его за интеграл; останется интеграл от
exp(g(x)-g(x_0)).
exp(g(x)-g(x_0)).
Victor Kleptsyn
М
18:22
Математические байки
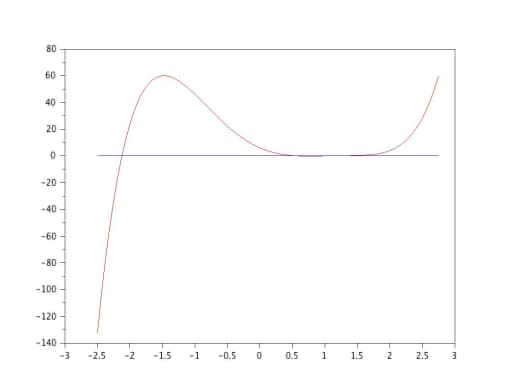
Вот как выглядит график подынтегральной функции при n=30:
Victor Kleptsyn
М
18:23
Математические байки
Правда, напоминает гауссовский колокол выше?
Victor Kleptsyn
М
18:23
Математические байки
На самом деле — он и есть (чем больше n, тем точнее).
Victor Kleptsyn
М
18:24
Математические байки
Потому что — посмотрим, как ведёт себя функция g(x)-g(n) рядом с точкой x=n, где её значение максимально.
Victor Kleptsyn
М
18:24
Математические байки
Значение, собственно, у неё там обращается в 0 — мы его вычли.
Victor Kleptsyn
М
18:25
Математические байки
Производной тоже нет: это точка максимума.
Victor Kleptsyn
М
18:25
Математические байки
Значит, первый нетривиальный член ряда Тейлора квадратичный;
g''(n) = -1/n,
поэтому
g''(n) = -1/n,
поэтому
Victor Kleptsyn
М
М
18:28
Математические байки
А тогда
Victor Kleptsyn
М
М
18:31
Математические байки
На самом деле, приближение выше хорошо работает не только при маленьких y, но при y порядка корня из n — а потом подынтегральная функция уже становится слишком маленькой.
Victor Kleptsyn
М
18:31
Математические байки
Поэтому гамма-функция Г(n) примерно равна произведению (n/e)^n на интеграл от e^{-y^2/2n}.
Victor Kleptsyn
М
18:32
Математические байки
Но e^{-y^2/2n} это почти плотность нормального распределения с дисперсией n — только её ещё нужно поделить на \sqrt{2\pi n}.
Victor Kleptsyn
М
18:32
Математические байки
Поделить — чтобы интеграл был единицей (ибо это полная вероятность).
Victor Kleptsyn
М
18:33
Математические байки
А значит, до деления он и равнялся \sqrt{2\pi n} — вот мы и видим, что у плотности нормального распределения он в знаменателе, а в формуле Стирлинга в качестве множителя.
Victor Kleptsyn
М
18:35
Математические байки
Но всё-таки, а откуда в гамма-функции ЦПТ, почему у нас тот самый гауссов интеграл получился?
Victor Kleptsyn
М
18:36
Математические байки
Ну, почему в числителе минус y^2, понятно: значение мы вычли, линейного слагаемого у ряда Тейлора в точке максимума не бывает, а вторая производная будет отрицательна. Пополам там тоже тейлоровский. А вот почему модуль второй производной оказался равен именно n, а не, скажем, n^2?
Victor Kleptsyn
М
18:38
Математические байки
Давайте возьмём распределение с плотностью e^{-x} на [0;+\infty) — его (логично) называют экспоненциальным распределением.
Victor Kleptsyn
М
18:41
Математические байки
(Кстати, если случайное время до какого-нибудь хорошего события — например, до прихода троллейбуса — распределено именно так, то это бывает грустно. Ведь если мы подождали, скажем, 10 минут, а троллейбус всё ещё не пришёл, то условное распределение того, сколько нам ещё остаётся ждать, ровно такое же.)
Victor Kleptsyn
М
18:42
Математические байки
Так вот — возьмём (n+1) случайную величину с таким распределением, и сложим.
Victor Kleptsyn
М
18:43
Математические байки
Плотность суммы независимых случайных величин это свёртка плотностей:
Victor Kleptsyn
М
М
18:44
Математические байки
Но экспоненты в произведении дают e^{-x}, а объём тетраэдра x_1+...+x_{n+1}=x как раз и равен x^n/n!.
Victor Kleptsyn
М
18:46
Математические байки
Поэтому сумма (n+1) такой случайной величины имеет плотность (x^n/n!) e^{-x}.
Victor Kleptsyn
М
18:47
Математические байки
То есть n! в знаменателе — тот самый, который мы приближаем, а x^n e^{-x} — та самая функция, что под интегралом в гамма-функции.
Victor Kleptsyn
М
18:48
Математические байки
Вот почему функция под интегралом превратилась в гауссово распределение — сумма (n+1) величины и должна себя вести как нормальное распределение, это и говорит ЦПТ!
Victor Kleptsyn
М
18:51
Математические байки
И вот почему в приближении там дисперсия n: потому что это сумма ~n одинаково распределённых слагаемых, каждое с дисперсией 1 — а дисперсия складывается.
Victor Kleptsyn
М
18:52
Математические байки
Да, а вообще такие распределения — плотность как у гамма-функции, нормированные на единицу — называют (логично) гамма-распределениями:
Victor Kleptsyn
М
М
18:54
Математические байки
И сумма двух величин, распределённых как гамма с параметрами a и b соответственно, оказывается распределённой как гамма с параметром a+b. А мы выше видели частных случай этого — для параметра a=1, который даёт просто экспоненциальное распределение.
Victor Kleptsyn
М
18:55
Математические байки
Ну вот, мы двумя способами и увидели множитель в формуле Стирлинга — а заодно посмотрели на центральную предельную теорему.
Victor Kleptsyn
М
18:56
Математические байки
И это, кажется, хороший момент на сегодня прекратить дозволенные речи.
Victor Kleptsyn
7 September 2019
М
20:44
Математические байки
Наверное, многие уже успели увидеть вот эту древнюю таблицу умножения —
Victor Kleptsyn
М
20:44
Математические байки
Н
Непрерывное математическое образование 31.08.2019 11:35:38
в качестве картинки перед новым учебным годом: таблица умножения (via https://vk.com/msu_mechmath)
«Вплоть до конца XVII века на Руси использовалась буквенная система записи цифр. Осуществлять сложные математические расчеты при помощи такой системы было невозможно, но для простых арифметических действий она вполне подходила, что и демонстрирует таблица умножения из рукописи XVII в.»
«Вплоть до конца XVII века на Руси использовалась буквенная система записи цифр. Осуществлять сложные математические расчеты при помощи такой системы было невозможно, но для простых арифметических действий она вполне подходила, что и демонстрирует таблица умножения из рукописи XVII в.»
Victor Kleptsyn
М
20:44
Математические байки
На эту таблицу умножения и впрямь интересно посмотреть.
Во-первых, она начинается с квадратов.
Во-вторых, произведения там только в порядке "большее на меньшее"
В-третьих, и это самое интересное: уже в столбце квадратов мы читаем Д*Д=SI
Во-первых, она начинается с квадратов.
Во-вторых, произведения там только в порядке "большее на меньшее"
В-третьих, и это самое интересное: уже в столбце квадратов мы читаем Д*Д=SI
Victor Kleptsyn
М
20:45
Математические байки
Так вот — SI это "шестнадцать", но первая цифра тут "шесть", а вторая "десять".
То есть и впрямь буквально "шестнадцать".
Ну и, например, З*В=ВI, "двенадцать".
А вот З*Г=КА, "двадцать один", и порядок возвращается к обычному для позиционной записи.
То есть и впрямь буквально "шестнадцать".
Ну и, например, З*В=ВI, "двенадцать".
А вот З*Г=КА, "двадцать один", и порядок возвращается к обычному для позиционной записи.
Victor Kleptsyn
М
21:09
Математические байки
===
Сегодняшняя байка — в начальной части скорее широко известная, а в заключительной скорее менее.
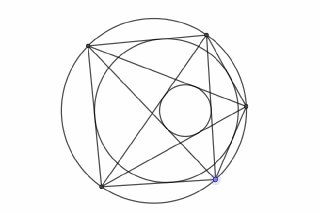
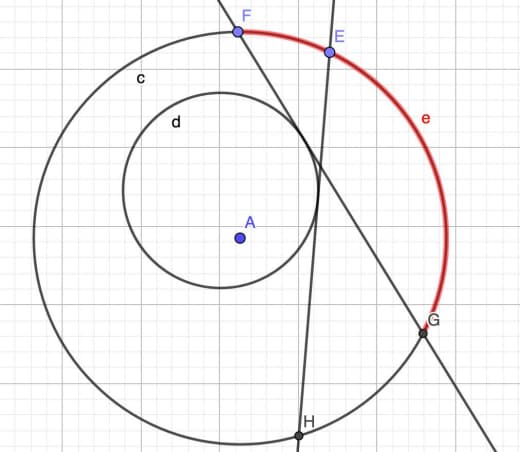
Если завращать гиперболу вокруг той её оси симметрии, которая её не пересекает, то получится однополостный гиперболоид. Например, если гипербола задавалась уравнением x^2-z^2=1, и вращаем вокруг оси Oz, то получится поверхность x^2+y^2-z^2=1.
И на этой поверхности есть два семейства прямых.
Больше ста лет назад инженер Владимир Григорьевич Шухов придумал красивую идею: пусть мы хотим построить башню, от которой нам нужна высота, но совершенно не обязательно, чтобы там было что-нибудь внутри.
Сегодняшняя байка — в начальной части скорее широко известная, а в заключительной скорее менее.
Если завращать гиперболу вокруг той её оси симметрии, которая её не пересекает, то получится однополостный гиперболоид. Например, если гипербола задавалась уравнением x^2-z^2=1, и вращаем вокруг оси Oz, то получится поверхность x^2+y^2-z^2=1.
И на этой поверхности есть два семейства прямых.
Больше ста лет назад инженер Владимир Григорьевич Шухов придумал красивую идею: пусть мы хотим построить башню, от которой нам нужна высота, но совершенно не обязательно, чтобы там было что-нибудь внутри.
Victor Kleptsyn
М
21:11
Математические байки
Например, водонапорная башня, или башня маяка.
Тогда такую башню можно собрать в виде ажурного гиперболоида — из прямых и скрепляющих их окружностей. И то, и другое (относительно) просто делается и собирается.
Тогда такую башню можно собрать в виде ажурного гиперболоида — из прямых и скрепляющих их окружностей. И то, и другое (относительно) просто делается и собирается.
Victor Kleptsyn
М
21:13
Математические байки
На сайте Математических Этюдов есть рассказ об этом,
http://www.etudes.ru/ru/etudes/shukhov-tower/ ,
который я очень советую — в том числе из-за исторических фотографий. Вот одна из них, водонапорной башни на выставке 1896 года:
http://www.etudes.ru/ru/etudes/shukhov-tower/ ,
который я очень советую — в том числе из-за исторических фотографий. Вот одна из них, водонапорной башни на выставке 1896 года:
Victor Kleptsyn
М
21:25
Математические байки
Вообще, гиперболических башен построили довольно много; я позволю себе ещё чуть-чуть процитировать сайт Этюдов —
Victor Kleptsyn
М
М
21:26
Математические байки
Есть, скажем, гиперболическая обзорная башня в Кобе в Японии —
Victor Kleptsyn
М
21:38
Математические байки
Но — самое знаменитое применение этой идеи это Шуховская (радио)башня высотой 150 метров. И тут возникает красивое развитие этой идеи — не надо строить высокие леса: можно собрать башню из гиперболических колец.
Сначала собирается первое. Потом внутри него собирается другое, и "за низ", через блоки наверху первого кольца, поднимается и пристыковывается к верху первого. Потом внутри собирается третье кольцо, и через блоки-"двуноги", которые уже есть наверху второго кольца, поднимается наверх и оно.
Иллюстрации с "Этюдов" —
Сначала собирается первое. Потом внутри него собирается другое, и "за низ", через блоки наверху первого кольца, поднимается и пристыковывается к верху первого. Потом внутри собирается третье кольцо, и через блоки-"двуноги", которые уже есть наверху второго кольца, поднимается наверх и оно.
Иллюстрации с "Этюдов" —
Victor Kleptsyn
М
21:42
Математические байки
Учитывая, что строили её в 1919-1922 годах; сразу после первой мировой войны и революции, и при идущей гражданской — кажется, без этих идей построить башню такой высоты просто бы не получилось.
Victor Kleptsyn
М
22:00
Математические байки
Так вот — давайте вернёмся к математике (а я ещё раз посоветую посмотреть страницу Этюдов об Шуховской башне, там есть ещё нетривиальные подробности).
Я начал с того, что на однополостном гиперболоиде есть два семейства прямых. А откуда мы знаем, что они там есть?
Как это ни смешно, если мы мотивируем этот вопрос именно ажурной башней, то от него можно попробовать "отбиться", сказав, что нам не так важно, чтобы поверхность была именно тем самым однополостным гиперболоидом, задающимся уравнением второго порядка. Важно лишь, чтобы это была поверхность вращения, на которой были бы два семейства пересекающихся прямых. Тогда мы соберём именно эту сетку из металлических брусьев — и скрепим их вдоль окружностей. А уж каким именно уравнением поверхность будет задаваться, это дело десятое. (Что, конечно, не совсем правда — нагрузки инженерам всё равно рассчитывать надо — но на нашем уровне аккуратности...)
Но такую поверхность можно получить, завращав вокруг (вертикальной) оси Oz любую скрещивающуюся с ней прямую L. Одно семейство прямых получится просто из образов L при вращении — а второе при его симметрии относительно любой плоскости, проходящей через ось Oz. Действительно, горизонтальные окружности, заметаемые точками L при вращении, такая симметрия сохраняет — а значит, сохраняет и всю поверхность, и образ семейства прямых это другое семейство прямых.
Я начал с того, что на однополостном гиперболоиде есть два семейства прямых. А откуда мы знаем, что они там есть?
Как это ни смешно, если мы мотивируем этот вопрос именно ажурной башней, то от него можно попробовать "отбиться", сказав, что нам не так важно, чтобы поверхность была именно тем самым однополостным гиперболоидом, задающимся уравнением второго порядка. Важно лишь, чтобы это была поверхность вращения, на которой были бы два семейства пересекающихся прямых. Тогда мы соберём именно эту сетку из металлических брусьев — и скрепим их вдоль окружностей. А уж каким именно уравнением поверхность будет задаваться, это дело десятое. (Что, конечно, не совсем правда — нагрузки инженерам всё равно рассчитывать надо — но на нашем уровне аккуратности...)
Но такую поверхность можно получить, завращав вокруг (вертикальной) оси Oz любую скрещивающуюся с ней прямую L. Одно семейство прямых получится просто из образов L при вращении — а второе при его симметрии относительно любой плоскости, проходящей через ось Oz. Действительно, горизонтальные окружности, заметаемые точками L при вращении, такая симметрия сохраняет — а значит, сохраняет и всю поверхность, и образ семейства прямых это другое семейство прямых.
Victor Kleptsyn
М
22:13
Математические байки
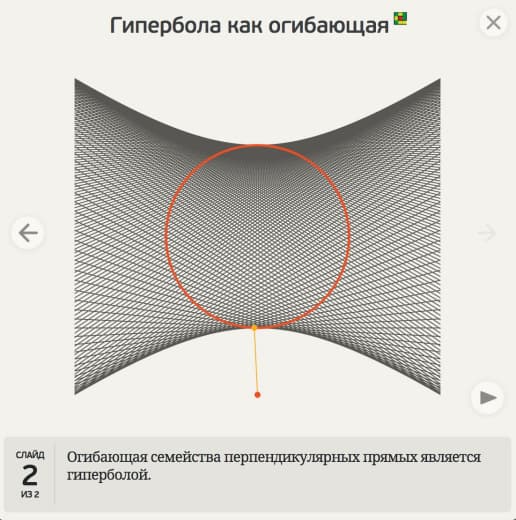
Кстати, с этим же связана выносящая мозг иллюстрация, когда прямой стержень вращается, проезжая через кривую -- гиперболическую -- прорезь:
https://youtu.be/N2exQpSuwi0?t=830
https://youtu.be/N2exQpSuwi0?t=830
Victor Kleptsyn
М
22:21
Математические байки
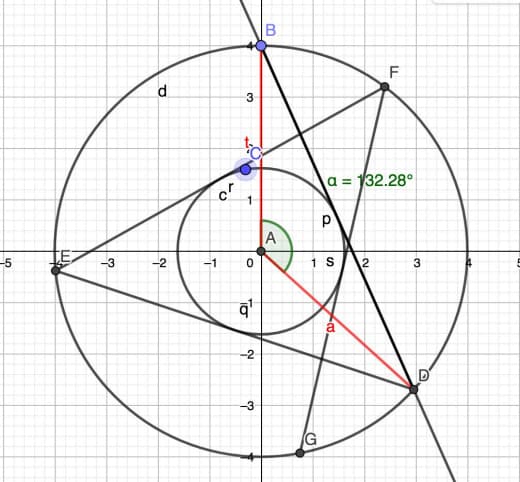
Но предположим, что мы хотим это знать именно про однополостный гиперболоид. Можно, например, взять уравнение гиперболоида выше, чуть-чуть его переписать, перенеся x^2 в правую часть —
y^2-z^2=1-x^2,
и сразу увидеть на нём две прямые, проходящие через "самую простую" точку (1,0,0):
x=1, y=±z.
Завращав их, получим оба семейства прямых. А нельзя ли обойтись без вращения?
И хорошо бы иметь рассуждение, применимое ко всем гиперболоидам — иначе нужно будет говорить слова "аффинное преобразование", переводить любой однополостный гиперболоид в канонический, и как-то это грустно...
y^2-z^2=1-x^2,
и сразу увидеть на нём две прямые, проходящие через "самую простую" точку (1,0,0):
x=1, y=±z.
Завращав их, получим оба семейства прямых. А нельзя ли обойтись без вращения?
И хорошо бы иметь рассуждение, применимое ко всем гиперболоидам — иначе нужно будет говорить слова "аффинное преобразование", переводить любой однополостный гиперболоид в канонический, и как-то это грустно...
Victor Kleptsyn
М
22:28
Математические байки
И тут есть рассуждение, которое пусть и не совсем строгое, но мне очень нравится: оно объясняет, что "иначе быть не может".
Давайте возьмём любую точку A — и проведём в ней касательную плоскость к гиперболоиду. Посмотрим, по какому множеству она его пересекает.
Для этого выберем на плоскости систему координат (s,t), выразим через них исходные координаты (x,y,z), и подставим результат в уравнение гиперболоида P(x,y,z)=0 — которое есть уравнение второй степени.
Естественно, систему координат на касательной плоскости мы выберем так, чтобы начальная точка A имела координаты (0,0).
Что за уравнение Q(s,t)=0 у нас получится?
Во-первых, оно второй степени. Во-вторых, Q(0,0)=0, потому что точка A была на гиперболоиде. В-третьих, линейных членов там тоже нет — потому что мы на касательной плоскости. Значит, Q(s,t) — это однородный многочлен второй степени.
Давайте возьмём любую точку A — и проведём в ней касательную плоскость к гиперболоиду. Посмотрим, по какому множеству она его пересекает.
Для этого выберем на плоскости систему координат (s,t), выразим через них исходные координаты (x,y,z), и подставим результат в уравнение гиперболоида P(x,y,z)=0 — которое есть уравнение второй степени.
Естественно, систему координат на касательной плоскости мы выберем так, чтобы начальная точка A имела координаты (0,0).
Что за уравнение Q(s,t)=0 у нас получится?
Во-первых, оно второй степени. Во-вторых, Q(0,0)=0, потому что точка A была на гиперболоиде. В-третьих, линейных членов там тоже нет — потому что мы на касательной плоскости. Значит, Q(s,t) — это однородный многочлен второй степени.
Victor Kleptsyn
М
22:43
Математические байки
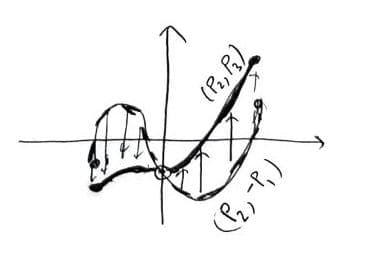
Если он невырожденный (что ещё нужно обосновывать), то с точностью до замены координат это либо сумма квадратов, либо разность. Если сумма квадратов, то пересечение гиперболоида с касательной плоскостью состояло бы только из одно точки A. А чисто геометрически гиперболоид выгнут "в разные стороны", так что ещё пересечения должны быть. "Значит" (кавычки, потому что "под ковёр" заметается слон упитанности большей, чем обычно), это разность квадратов — а тогда она и задаёт две пересекающиеся прямые. Которые лежат в исходном гиперболоиде, ибо это было пересечение с ним!
То есть а) через любую точку гиперболоида проходят две пересекающиеся прямые и
б) у этих прямых есть хорошее геометрическое описание — их высекает проведённая в этой точке касательная плоскость. (Что, постфактум, совершенно очевидно, но то постфактум.)
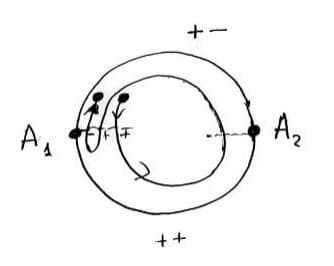
Ну и, если вспомнить, что сумма квадратов s^2+t^2=0 тоже задаёт две пересекающиеся прямые, только мнимые, s=±it, то можно добавить, что на (комплексифицированной) сфере x^2+y^2+z^2=1 тоже есть прямые, только мнимые, и искать их можно точно так же — пересечением с касательной плоскостью.
То есть а) через любую точку гиперболоида проходят две пересекающиеся прямые и
б) у этих прямых есть хорошее геометрическое описание — их высекает проведённая в этой точке касательная плоскость. (Что, постфактум, совершенно очевидно, но то постфактум.)
Ну и, если вспомнить, что сумма квадратов s^2+t^2=0 тоже задаёт две пересекающиеся прямые, только мнимые, s=±it, то можно добавить, что на (комплексифицированной) сфере x^2+y^2+z^2=1 тоже есть прямые, только мнимые, и искать их можно точно так же — пересечением с касательной плоскостью.
Victor Kleptsyn
М
22:55
Математические байки
В качестве ответвления — как раз наличие прямых на поверхностях второго порядка играет в сведении (преобразованиями Чирнгауз[ен]а) любого уравнения пятой степени к уравнению вида y^5+ay+1=0. После чего можно говорить, что "его решение это просто ещё одна функция от одной переменной a, и чем она хуже, чем степени, радикалы, или синус с тангенсом, кроме как исторически?". (И именно поэтому в формулировке 13-й проблемы Гильберта отдельно оговаривались многочлены именно седьмой степени — это первая степень, где оставалось три свободных параметра.)
Victor Kleptsyn
М
22:57
Математические байки
Но это история не на сейчас... :)
Victor Kleptsyn
21 September 2019
М
21:16
Математические байки
In reply to this message
Раз я в прошлый раз прервался на преобразованиях Чирнгаузена — может быть, это стоит рассказать: кажется, вот это знают не все. Правда, сначала будет более общеизвестное предисловие.
Victor Kleptsyn
М
21:17
Математические байки
Есть несколько стандартных способов решать кубические уравнения. Самый, пожалуй, известный, это сначала сдвигом переменной привести его к виду x^3+px+q=0, после чего заметить, что выражение
x^3+y^3+z^3-3xyz
раскладывается на множители, одним из которых будет (x+y+z).
Остаётся найти такие y и z, чтобы p=-3yz и q=y^3+z^3, а это (по теореме Виета) превращается в квадратное уравнение с корнями y^3 и z^3.
x^3+y^3+z^3-3xyz
раскладывается на множители, одним из которых будет (x+y+z).
Остаётся найти такие y и z, чтобы p=-3yz и q=y^3+z^3, а это (по теореме Виета) превращается в квадратное уравнение с корнями y^3 и z^3.
Victor Kleptsyn
М
21:20
Математические байки
Чуть менее известный, но глобально чуть более "правильный", связан с теорией Галуа.
Victor Kleptsyn
М
21:20
Математические байки
Любой симметрический многочлен выражается через элементарные симметрические. Поэтому любой симметрический многочлен от корней полинома выражается через его коэффициенты. Так мы решаем квадратное уравнение — сумма корней x_1+x_2 уже симметрическая, а разность x_1-x_2 при их перестановке меняет знак, так что (x_1-x_2)^2 тоже выражается через коэффициенты исходного уравнения. Остаётся извлечь корень и восстановить x_1 и x_2 по их сумме и разности.
Victor Kleptsyn
М
21:23
Математические байки
Так же, но чуть более сложно решается кубическое уравнение — берутся уже три линейные комбинации корней,
S=x_1+x_2+x_3,
A=x_1+w x_2+ w^2 x_3,
B=x_1+w^2 x_2 + w x_3,
где w=exp(2πi/3) — корень кубический из единицы.
Тогда S уже симметрический, а A и B при циклической перестановке корней умножатся на w и на w^2 соответственно. Поэтому A^3 и B^3 сохраняются при циклической перестановке корней. А транспозиция меняет их местами — то есть они ведут себя как корни квадратного уравнения, коэффициенты которого (равные -(A^3+B^3) и A^3*B^3) являются уже полностью симметрическими многочленами от x_1,x_2,x_3.
Остаётся "открутить всё назад":
-решить квадратное уравнение, чтобы найти A^3 и B^3,
- извлечь кубические корни, найдя A и B,
- и решить систему из трёх линейных уравнений на три неизвестных.
S=x_1+x_2+x_3,
A=x_1+w x_2+ w^2 x_3,
B=x_1+w^2 x_2 + w x_3,
где w=exp(2πi/3) — корень кубический из единицы.
Тогда S уже симметрический, а A и B при циклической перестановке корней умножатся на w и на w^2 соответственно. Поэтому A^3 и B^3 сохраняются при циклической перестановке корней. А транспозиция меняет их местами — то есть они ведут себя как корни квадратного уравнения, коэффициенты которого (равные -(A^3+B^3) и A^3*B^3) являются уже полностью симметрическими многочленами от x_1,x_2,x_3.
Остаётся "открутить всё назад":
-решить квадратное уравнение, чтобы найти A^3 и B^3,
- извлечь кубические корни, найдя A и B,
- и решить систему из трёх линейных уравнений на три неизвестных.
Victor Kleptsyn
М
21:24
Математические байки
И если последить, то здесь как раз возникает последовательность разрешимости группы Sym_3 перестановок трёх корней, и это дорога к теории Галуа — но это меня унесло в сторону, а байка, собственно, и не об этом.
Да, для полноты, пара ссылок —
- Э. Б. Винберг, "Курс алгебры", глава 3, параграф 9, с. 145;
- D. Cox, "Galois theory", chapter 1 "Cubic equations".
Да, для полноты, пара ссылок —
- Э. Б. Винберг, "Курс алгебры", глава 3, параграф 9, с. 145;
- D. Cox, "Galois theory", chapter 1 "Cubic equations".
Victor Kleptsyn
М
21:24
Математические байки
А хочу я рассказать о третьем, ещё менее популярном способе решать и упрощать уравнения, о преобразованиях Чирнгауза. Да, если что — Чирнгауз вот этот:
http://www-history.mcs.st-andrews.ac.uk/Biographies/Tschirnhaus.html
https://en.wikipedia.org/wiki/Ehrenfried_Walther_von_Tschirnhaus
http://www-history.mcs.st-andrews.ac.uk/Biographies/Tschirnhaus.html
https://en.wikipedia.org/wiki/Ehrenfried_Walther_von_Tschirnhaus
Victor Kleptsyn
М
21:27
Математические байки
Правда, почему-то преобразования иногда называют Чирнгауза, а иногда Чирнгаузена — см.
http://mathworld.wolfram.com/TschirnhausenTransformation.html или http://mi.mathnet.ru/uzku407 ;
так и в комментариях Витушкина к 13-й проблеме Гильберта:
http://mathworld.wolfram.com/TschirnhausenTransformation.html или http://mi.mathnet.ru/uzku407 ;
так и в комментариях Витушкина к 13-й проблеме Гильберта:
Victor Kleptsyn
М
21:27
Математические байки
И откуда взялось это "ен", я не знаю.
Victor Kleptsyn
М
21:28
Математические байки
Так вот. Пусть у нас есть уравнение P(x)=0 какой-то степени k. И многочлен y=Q(x) меньшей степени.
Тогда можно взять корни x_1,...,x_k многочлена P, и построить новый многочлен R(y) с корнями y_1,...,y_k, получающимися как y_j=Q(x_j).
Тогда можно взять корни x_1,...,x_k многочлена P, и построить новый многочлен R(y) с корнями y_1,...,y_k, получающимися как y_j=Q(x_j).
Victor Kleptsyn
М
21:29
Математические байки
И может быть, новое уравнение R(y)=0 будет проще старого, а тогда, найдя y_j, мы придём к задаче решения уравнений меньшей степени Q(x)=y_j.
Например, так решается квадратное уравнение
x^2+px+q=0:
мы делаем замену y=x+p/2, после чего приходим к более простому уравнению
y^2-(p^2/4 - q)=0,
которое и решаем извлечением квадратного корня — после чего возвращаемся к исходной переменной.
Например, так решается квадратное уравнение
x^2+px+q=0:
мы делаем замену y=x+p/2, после чего приходим к более простому уравнению
y^2-(p^2/4 - q)=0,
которое и решаем извлечением квадратного корня — после чего возвращаемся к исходной переменной.
Victor Kleptsyn
М
21:29
Математические байки
Для кубического уравнения линейной заменой можно убить только коэффициент при x^2. Но что, если мы рассмотрим многочлены Q и второй степени тоже?
Оказывается, тогда можно обнулить и коэффициент при x. И получится уравнение y^3+c=0, которое решается простым извлечением кубического корня!
Оказывается, тогда можно обнулить и коэффициент при x. И получится уравнение y^3+c=0, которое решается простым извлечением кубического корня!
Victor Kleptsyn
М
21:31
Математические байки
И сделать это достаточно просто. Действительно, коэффициенты многочлена с корнями в y_i находятся по теореме Виета. Соответственно, нам нужно, чтобы сумма, и сумма попарных произведений y_i равнялась бы нулю.
Victor Kleptsyn
М
21:34
Математические байки
А это то же самое, что попросить, чтобы сумма y_i и сумма квадратов y_i равнялась бы нулю.
Уравнение на сумму — линейное уравнение на коэффициенты, на сумму квадратов — квадратное.
Уравнение на сумму — линейное уравнение на коэффициенты, на сумму квадратов — квадратное.
Victor Kleptsyn
М
21:34
Математические байки
Уравнение на сумму — линейное уравнение на коэффициенты, на сумму квадратов — квадратное.
И ещё остаётся одна "неважная" степень свободы: можно все y_i одновременно умножить на константу. Чтобы её убрать, проще всего зафиксировать у многочлена Q какой-нибудь один коэффициент — проще всего сказать, что мы будем искать многочлен y=Q(x) в виде Q(x)=x+b_0+b_2 x^2.
И тогда условие на сумму позволяет линейно выразить b_0 через b_2, а условие на сумму квадратов становится квадратным уравнением на оставшийся неизвестный коэффициент.
И ещё остаётся одна "неважная" степень свободы: можно все y_i одновременно умножить на константу. Чтобы её убрать, проще всего зафиксировать у многочлена Q какой-нибудь один коэффициент — проще всего сказать, что мы будем искать многочлен y=Q(x) в виде Q(x)=x+b_0+b_2 x^2.
И тогда условие на сумму позволяет линейно выразить b_0 через b_2, а условие на сумму квадратов становится квадратным уравнением на оставшийся неизвестный коэффициент.
Victor Kleptsyn
М
21:35
Математические байки
Решив его — мы сводим исходное уравнение к уравнению вида y^3+c=0, решаем его, и затем "возвращаемся обратно", решая квадратные уравнения Q(x_i)=y_i.
Victor Kleptsyn
М
21:36
Математические байки
===
Если попытаться решить уравнение 4-й степени тем же преобразованием "в лоб", то получится система из линейного уравнения (сумма y_i нулевая), квадратного (сумма квадратов y_i), и кубического (сумма кубов). И если всё выражать "в лоб", то будет уравнение 1*2*3=6-й степени на коэффициенты преобразования. Свести уравнение 4-й степени к уравнению 6-й не выглядит победой...
Если попытаться решить уравнение 4-й степени тем же преобразованием "в лоб", то получится система из линейного уравнения (сумма y_i нулевая), квадратного (сумма квадратов y_i), и кубического (сумма кубов). И если всё выражать "в лоб", то будет уравнение 1*2*3=6-й степени на коэффициенты преобразования. Свести уравнение 4-й степени к уравнению 6-й не выглядит победой...
Victor Kleptsyn
М
21:38
Математические байки
Но можно сделать так — прибить только коэффициенты при y и при y^3. И нахождение такого Q будет только кубическим уравнением, которое мы уже научились решать.
Собственно, раз у нас только два уравнения — хватит даже квадратного многочлена Q,
y=Q(x)= x+ b_0+ b_2 x^2.
Тогда линейное условие позволяет выразить b_0 через b_2, а условие на сумму произведений y_i по три (увы, тут упрощения уже нет, и придётся повозиться) — становится кубическим уравнением на оставшуюся переменную.
Собственно, раз у нас только два уравнения — хватит даже квадратного многочлена Q,
y=Q(x)= x+ b_0+ b_2 x^2.
Тогда линейное условие позволяет выразить b_0 через b_2, а условие на сумму произведений y_i по три (увы, тут упрощения уже нет, и придётся повозиться) — становится кубическим уравнением на оставшуюся переменную.
Victor Kleptsyn
М
21:38
Математические байки
После такого преобразования, раз мы прибили коэффициенты при y и при y^3 — остаётся биквадратное уравнение!
Victor Kleptsyn
М
21:39
Математические байки
А его уже можно решить — ну и дальше вернуться обратно.
Victor Kleptsyn
М
21:39
Математические байки
===
Для уравнения 5-й степени ничего такого, естественно, не проходит: обнуление коэффициентов при y^4, y^3,..., y^1 это уже уравнения 1, 2, 3, 4 степени соответственно — и в итоге получается уравнение 24-й степени, которое никак не решить.
Для уравнения 5-й степени ничего такого, естественно, не проходит: обнуление коэффициентов при y^4, y^3,..., y^1 это уже уравнения 1, 2, 3, 4 степени соответственно — и в итоге получается уравнение 24-й степени, которое никак не решить.
Victor Kleptsyn
М
21:40
Математические байки
Но можно привести уравнение к виду y^5+ay+1=0.
Действительно: когда мы задаём y=Q(x)=b_4 x^4 + ... + b_1 x + b_0, то у нас пять неизвестных коэффициентов; их можно все одновременно умножать на константу, так что пока зафиксируем, например, b_1=1.
Условие обнуления суммы y_i — линейное условие на коэффициенты. Поэтому остаётся 3 неизвестных коэффициента.
Действительно: когда мы задаём y=Q(x)=b_4 x^4 + ... + b_1 x + b_0, то у нас пять неизвестных коэффициентов; их можно все одновременно умножать на константу, так что пока зафиксируем, например, b_1=1.
Условие обнуления суммы y_i — линейное условие на коэффициенты. Поэтому остаётся 3 неизвестных коэффициента.
Victor Kleptsyn
М
21:40
Математические байки
Остаётся обнулить сумму квадратов и сумму кубов. Если идти "в лоб", то получится уравнение 6-й степени, с которым не очень-то поработаешь. Но!
Victor Kleptsyn
М
21:41
Математические байки
Условие обнуления суммы квадратов y_i — это квадратичное условие, и мы получаем квадратичную поверхность в пространстве (из трёх ещё неизвестных коэффициентов). Как раз такую, какую мы обсуждали в контексте Шуховской башни.
Так давайте на этой поверхности найдём (комплексную, если надо) прямую, хотя бы одну!
Так давайте на этой поверхности найдём (комплексную, если надо) прямую, хотя бы одну!
Victor Kleptsyn
М
21:42
Математические байки
И вместо того, чтобы с корнями выражать коэффициенты — просто ограничимся на неё, заплатив потерей степени свободы за отсутствие корней из неизвестных.
Тогда на этой прямой останется только кубическое уравнение на обнуление суммы кубов y_i — которое мы уже умеем решать.
Тогда на этой прямой останется только кубическое уравнение на обнуление суммы кубов y_i — которое мы уже умеем решать.
Victor Kleptsyn
М
21:42
Математические байки
Так что любое уравнение 5 степени можно свести к уравнению вида
y^5+a y + 1=0
(потому что свободный член можно всегда загнать в 1 изменением масштаба).
y^5+a y + 1=0
(потому что свободный член можно всегда загнать в 1 изменением масштаба).
Victor Kleptsyn
М
21:44
Математические байки
Да, ссылка —
В. В. Прасолов, "Многочлены" (файл книги есть тут —
https://www.mccme.ru/prasolov/ — в списке под номером 11), с. 187.
В. В. Прасолов, "Многочлены" (файл книги есть тут —
https://www.mccme.ru/prasolov/ — в списке под номером 11), с. 187.
Victor Kleptsyn
М
21:46
Математические байки
Ну и — можно говорить, что функция y(a) одной переменной "корень уравнения
y^5+ay+1=0
с параметром a" ничем не хуже кучи остальных функций одной переменной (будь то хоть корень, хоть синус, хоть тангенс), кроме того, что она нам в школе не встречалась.
y^5+ay+1=0
с параметром a" ничем не хуже кучи остальных функций одной переменной (будь то хоть корень, хоть синус, хоть тангенс), кроме того, что она нам в школе не встречалась.
Victor Kleptsyn
М
21:53
Математические байки
И это (а, точнее, аналогичные рассуждения с функциями двух переменных) были мотивировкой 13-й проблемы Гильберта — с совершенно удивительным ответом.
Но про это я напишу чуть позже, а пока я собираюсь вернуться к простой геометрии.
А именно ("в следующей серии") — к вопросу о том, сколько прямых пересекают заданную четвёрку скрещивающихся прямых в трёхмерном пространстве. Оказывается, на этот вопрос можно, естественно, смотреть геометрически — а можно с точки зрения линейной алгебры, где, удивительным образом, возникают собственные вектора. Но это тоже будет в следующей серии — а на сегодня, кажется, настало время прекратить дозволенные речи.
Но про это я напишу чуть позже, а пока я собираюсь вернуться к простой геометрии.
А именно ("в следующей серии") — к вопросу о том, сколько прямых пересекают заданную четвёрку скрещивающихся прямых в трёхмерном пространстве. Оказывается, на этот вопрос можно, естественно, смотреть геометрически — а можно с точки зрения линейной алгебры, где, удивительным образом, возникают собственные вектора. Но это тоже будет в следующей серии — а на сегодня, кажется, настало время прекратить дозволенные речи.
Victor Kleptsyn
15 October 2019
М
19:28
Математические байки
===
Как-то давно я не писал, это надо исправлять. Тем более, что и повод есть — у нас сегодня в Ренне было открытие амфитеатра имени Мариам Мирзахани:
https://irmar.univ-rennes1.fr/actualites/journee-dinauguration-de-lamphitheatre-maryam-mirzakhani
И пару сюжетов мне хочется пересказать.
Как-то давно я не писал, это надо исправлять. Тем более, что и повод есть — у нас сегодня в Ренне было открытие амфитеатра имени Мариам Мирзахани:
https://irmar.univ-rennes1.fr/actualites/journee-dinauguration-de-lamphitheatre-maryam-mirzakhani
И пару сюжетов мне хочется пересказать.
Victor Kleptsyn
М
19:31
Математические байки
Да, на всякий случай: вот слайд из рассказа Elise Goujard —
Victor Kleptsyn
М
19:31
Математические байки
А уже в 2017-м Мирзахани не стало. Рак. :(
Victor Kleptsyn
М
19:32
Математические байки
Так вот — я начну с рассказа Ольги Paris-Ромаскевич:
Victor Kleptsyn
М
19:37
Математические байки
Предположим, что мы взяли материал с коэффициентом преломления (-1). Школьный курс физики должен вызывать ощущение, что это странно — в обычной ситуации коэффициент преломления должен быть не просто положительным, а больше единицы (ибо скорость света в среде и всё такое), но метаматериалы такие бывают (тут могла бы быть дискуссия о разных скоростях — фазовая скорость не равно скорость распространения информации — но давайте я не буду лезть в чужую область, а предложу — следуя Ольге — рассмотреть такую модель).
Victor Kleptsyn
М
19:39
Математические байки
А теперь представим себе, что мы на плоскости взяли паркет, в котором часть плиток с коэффициентом преломления +1 ("воздух"), а другие — с коэффициентом преломления (-1).
Victor Kleptsyn
М
19:41
Математические байки
Тогда закон преломления для луча света, летящего через такой паркет, будет гласить — при пересечении границы между плитками луч продолжается, отражаясь симметрично относительно этой границы.
Вполне забавная постановка — и тут появляются интересные эффекты.
Вполне забавная постановка — и тут появляются интересные эффекты.
Victor Kleptsyn
М
19:42
Математические байки
Вот так луч проходит через несколько параллельных границ
Victor Kleptsyn
М
19:43
Математические байки
А вот так — лучи могут отражаться вокруг точки, где сходятся шесть правильных треугольников.
Victor Kleptsyn
М
19:44
Математические байки
Собственно, если взять паркет из правильных треугольников или из квадратов, то _все_ траектории замкнутся.
Victor Kleptsyn
М
19:47
Математические байки
К такому бильярдный народ совершенно не привычен — а аналогия, которую тут приводила Ольга, это задача двух тел (если энергия достаточно небольшая, чтобы планета не улетела — то орбита будет периодической)
Victor Kleptsyn
М
19:47
Математические байки
Вопрос — а что будет для других паркетов? Например — для паркета из неправильных треугольников?
Victor Kleptsyn
М
19:47
Математические байки
И вот тут начинается интересное.
Victor Kleptsyn
М
19:50
Математические байки
Во-первых, бывают более сложные периодические траектории. И бывают траектории, линейно убегающие на бесконечность — периодичным или даже не-периодичным (с учётом сдвига) образом.
Victor Kleptsyn
М
19:52
Математические байки
А может ли траектория быть неограниченной, но не убегать на бесконечность? Улетели на расстояние 100 от начальной точки, преломления её развернули, вернулись, улетели на расстояние 1000, развернулись, вернулись, и так далее?
Victor Kleptsyn
М
19:52
Математические байки
Оказывается, нет, не может!
Victor Kleptsyn
М
19:55
Математические байки
Более того, траектория, просто два раза подряд вернувшаяся в один и тот же треугольник, уже обязана оказаться периодической — и зациклиться уже в этот момент. А если траектория периодическая, и её начальное условие чуть-чуть пошевелить (наклонить-сдвинуть), то она останется периодической.
Victor Kleptsyn
М
19:58
Математические байки
И у этого есть очень простое и красивое объяснение. Дело в том, что простейший паркет из одинаковых треугольников можно "сложить" — складывая/отражая относительно каждого ребра.
Если говорить формально, то такое "складывание" это (не-взаимно-однозначное) непрерывное отображение из плоскости в плоскость, которое есть изометрия на каждом отдельном треугольнике, а на любые два соседних его ограничения отличаются на симметрию.
Если говорить формально, то такое "складывание" это (не-взаимно-однозначное) непрерывное отображение из плоскости в плоскость, которое есть изометрия на каждом отдельном треугольнике, а на любые два соседних его ограничения отличаются на симметрию.
Victor Kleptsyn
М
19:58
Математические байки
Но картинки тут, кажется, понятнее:
Victor Kleptsyn
М
20:01
Математические байки
Так вот — магия состоит в том, что при таком складывании отрезки траектории луча переходят на одну и ту же прямую.
Victor Kleptsyn
М
20:03
Математические байки
А тогда, вернувшись в какой-то треугольник, мы можем пересечь его только по тому же самому отрезку, что и в первый раз — ведь складывающее отображение (по индукции) всю траекторию переводит в одну прямую.
Victor Kleptsyn
М
20:07
Математические байки
(Да, из ответвлений: мне ситуация, когда складывания переводят что-то в одну прямую, напомнила немного мультик "одним разрезом" — http://www.etudes.ru/ru/etudes/fold-cut-problem/ — но может быть, это далёкая ассоциация... Хотя, наверное, не так и безумно далёкая: если складывание уже есть, то разрезав по этой прямой ножницами/гильотиной, мы как раз путь луча и получим)
Victor Kleptsyn
М
20:08
Математические байки
In reply to this message
Вот всё и доказано. И в частности, траектория луча не может самопересечься — что совершенно не так, например, в бильярдах.
Victor Kleptsyn
М
20:09
Математические байки
Но и это ещё не всё. Посмотрим ещё на периодические траектории:
Victor Kleptsyn
М
20:11
Математические байки
Каждый раз множество вершин и рёбер, попавших внутрь траектории, образует дерево. Не бывает так, чтобы внутри содержался целый треугольник, куда траектория не заходила бы.
А всегда ли это так?
А всегда ли это так?
Victor Kleptsyn
М
20:13
Математические байки
Теорема (Olga Paris-Romaskevich): Да, всегда.
Victor Kleptsyn
М
М
20:14
Математические байки
(Отсюда — https://hal.archives-ouvertes.fr/hal-02169195 )
Victor Kleptsyn
М
20:17
Математические байки
Доказательство. Любую траекторию (в частности, периодическую) можно включить в "слоение" плоскости: плоскость-образ после складывания можно нарезать на параллельные прямые, а потом взять полный прообраз этой нарезки. Получаются вот такие красивые картинки:
Victor Kleptsyn
М
20:18
Математические байки
Но если есть периодическая траектория — можно её сдвигать "внутрь", пока не получится особая траектория — входящая и выходящая из какой-нибудь из вершин:
Victor Kleptsyn
М
20:21
Математические байки
Назовём такую траекторию цветком (точнее, объединение всех траекторий слоения, проходящих через данную вершину: мы не можем говорить о траектории после входа в вершину).
Victor Kleptsyn
М
20:22
Математические байки
Так вот — оказывается, что часть теоретически возможных вариантов поведения для цветка запрещена:
Victor Kleptsyn
М
20:28
Математические байки
После чего можно запускать индукцию, сжимая и сжимая траекторию дальше (выкидывая вершину цветка) — мешали этому только запрещённые варианты.
Victor Kleptsyn
М
20:31
Математические байки
In reply to this message
А, ещё вот такая картинка для определения слоения, кажется, более наглядная:
Victor Kleptsyn
М
М
20:34
Математические байки
Правда, доказано по модулю того, почему именно для цветов запрещено то, что запрещено — а это как раз важная и смысловая часть.
Victor Kleptsyn
М
20:35
Математические байки
Две вещи, которые используются в её доказательстве (и тут я начинаю говорить уже совсем пунктиром):
Victor Kleptsyn
М
20:36
Математические байки
- Радиальное слоение. Можно на плоскости после складывания взять не нарезку на параллельные прямые, а нарезку на прямые, проходящие через вершину треугольника. И, опять-таки, взять у них прообраз:
Victor Kleptsyn
М
20:37
Математические байки
Всё ещё получается (особое) слоение — раз на плоскости после складывания они, кроме как в вершине, не пересекались, то и про прообразы то же самое можно сказать.
Victor Kleptsyn
М
20:40
Математические байки
Инструмент второй — символическая динамика: можно записывать/кодировать буквами a,b,c, какие именно стороны треугольников пересекает траектория:
Victor Kleptsyn
М
20:41
Математические байки
(А вот — картинка даже для случая четырёхугольника, там уже a,b,c,d)
Victor Kleptsyn
М
20:46
Математические байки
Ну вот с их помощью (уже не буду говорить, как) теорему о запрещённых цветках — а через неё и теорему о дереве — Ольга и доказывает.
Victor Kleptsyn
М
20:47
Математические байки
А вот мультфильм с визуализацией этого, который был показан под конец лекции. Теперь вы знаете всё, что там появляется:
https://www.youtube.com/watch?v=t1r1cO1V35I
https://www.youtube.com/watch?v=t1r1cO1V35I
Victor Kleptsyn
М
20:50
Математические байки
Пара кадров оттуда —
Victor Kleptsyn
М
20:54
Математические байки
И последний, ещё наглядный, но уже более сложный аккорд — это сложность траекторий.
Victor Kleptsyn
М
21:01
Математические байки
In reply to this message
Вот мы видели периодические и линейно убегающие на бесконечность траектории. А что-нибудь ещё бывает? И насколько сложными бывают периодические траектории? И каким может быть набор всех траекторий для данного треугольного паркета?
Victor Kleptsyn
М
21:02
Математические байки
Всё зависит от того, из каких именно треугольников собран паркет:
Victor Kleptsyn
М
21:03
Математические байки
Для некоторых (например, для правильного) — периодичны все траектории.
Victor Kleptsyn
М
21:03
Математические байки
Для некоторых — часть траекторий периодична, а часть убегает на бесконечность с линейной скоростью.
Victor Kleptsyn
М
21:05
Математические байки
(и это как раз типичный случай.)
Victor Kleptsyn
М
21:13
Математические байки
А есть — очень хитрые: для них (почти все) траектории, которые проходят через центр описанной окружности, посещают (либо в прошлом, либо в будущем) все вообще плитки. То есть это убегание на бесконечность, но гораздо более медленное. А не-проходящие — периодичны, но чем ближе траектория к проходящей через центр, тем больше у неё период.
Более того, эти периоды — удвоенные элементы последовательности Трибоначчи (1,1,1,3, следующее = сумма трёх предыдущих, так что получается
1,1,1,3,5,9,17,...).
2*1, правда, не бывает, зато бывает остальное — 2*3=6, 2*5=10,...
Более того, эти периоды — удвоенные элементы последовательности Трибоначчи (1,1,1,3, следующее = сумма трёх предыдущих, так что получается
1,1,1,3,5,9,17,...).
2*1, правда, не бывает, зато бывает остальное — 2*3=6, 2*5=10,...
Victor Kleptsyn
М
21:15
Математические байки
Треугольник для этого должен быть с очень специальными углами — вообще, тут (сейчас скажу, почему) играют углы, а не, например, длины сторон или что-нибудь ещё.
Victor Kleptsyn
М
21:23
Математические байки
Уравнение a+a^2+a^3=1 — то самое, которое играет роль во фрактале Рози. Который сам по себе тема для отдельной байки, а пока лишь пара картинок и ссылок...
Victor Kleptsyn
М
21:23
Математические байки
1) https://en.wikipedia.org/wiki/Rauzy_fractal + картинка из Википедии:
Victor Kleptsyn
М
21:24
Математические байки
https://www.mccme.ru/dubna/2014/courses/kanel-mitrofanov.htm — связанный с этим курс;
Victor Kleptsyn
М
21:25
Математические байки
https://youtu.be/fMJflV_GUpU?t=231 — а вот и настоящий паркет из дерева...
Victor Kleptsyn
М
21:27
Математические байки
Ну и на сейчас хватит — в общем, красивый самоподобный объект. Так вот, периодические траектории в паркете с тем самым Рози-треугольником, когда они становятся всё больше и больше (начинаясь близко к центру описанной окружности) — становятся похожи на этот самый фрактал Рози!
Victor Kleptsyn
М
21:48
Математические байки
И я обещал рукомахательное объяснение про углы. Оказывается, динамика того, что происходит с траекторией, описывается перекладыванием отрезков со сдвигом и переворотом. И длины там как раз отвечают углам треугольника.
Victor Kleptsyn
М
21:57
Математические байки
(И это совсем несложно увидеть, но уже точно не в этот раз...)
Пара картинок в завершение рассказа:
Пара картинок в завершение рассказа:
Victor Kleptsyn
М
21:58
Математические байки
(перекладывания со сдвигом и переворотом)
Victor Kleptsyn
М
21:58
Математические байки
Теорема о том, что траектория через центр окружности в исключительном бильярде проходит через все плитки:
Victor Kleptsyn
М
М
22:00
Математические байки
Особенно красив второй случай: если с одной из сторон такая траектория втыкается в вершину, то из этой вершины растёт цветок из шести таких траекторий, и посещают все треугольники они уже все вместе.
Victor Kleptsyn
М
22:01
Математические байки
Да, "работа над ошибками" — я поторопился в начале сказать, что для квадратного паркета периодичны все траектории. Это для паркета из правильных треугольников так, а для квадратного, если луч соединяет две противоположные стороны, то он как раз линейно убежит на бесконечность.
Victor Kleptsyn
М
22:06
Математические байки
In reply to this message
Последнее — преобразования перекладывания отрезков это совершенно огромная область (с чем только не связанная). Даже перечислять не буду, а то до завтра не закончу. И индукция Рози (а Рози тот же) как раз оттуда. И похожий на треугольник Серпинского (и даже ему гомеоморфный, но определяемый с помощью проективных отображений) Rauzy gasket, который появлялся в левом верхнем углу на том фото, где описывалось поведение траекторий — оттуда же.
Victor Kleptsyn
М
22:07
Математические байки
Ну и на этом я хочу на сегодня прекратить дозволенные речи...
Victor Kleptsyn
21 October 2019
М
12:33
Математические байки
In reply to this message
Ещё одна байка с прошлого раза — это рассказ Elise Goujard (в тот же день) на "пятиминутке Лебега".
В Ренне раз в неделю есть жанр популярных рассказов коллегам и широкой публике — на пять минут. Буквально — с таймером, тикающим обратным отсчётом от 5:00.
Рассказывают как присутствующим — так и выкладывают в интернет:
https://www.lebesgue.fr/5min
или
https://www.youtube.com/watch?v=184oPJA-CPw&list=PLZ5ZEffH1cUAkodxGDs0SNif_wScXNTU0
В Ренне раз в неделю есть жанр популярных рассказов коллегам и широкой публике — на пять минут. Буквально — с таймером, тикающим обратным отсчётом от 5:00.
Рассказывают как присутствующим — так и выкладывают в интернет:
https://www.lebesgue.fr/5min
или
https://www.youtube.com/watch?v=184oPJA-CPw&list=PLZ5ZEffH1cUAkodxGDs0SNif_wScXNTU0
Victor Kleptsyn
М
12:35
Математические байки
Получается, как мне кажется, очень удачный жанр (большая аудитория у нас обычно заполняется полностью). Так вот — Элиза во вторник рассказывала и там, и рассказывала про задачу о зеркальной комнате и теорему о волшебной палочке.
Вопрос: пусть у нас есть комната, ограниченная идеальными зеркалами. Можно ли там поставить точечный источник света так, чтобы в результате комната была освещена целиком? Или, может быть, свечку вообще можно ставить почти куда угодно — ведь свет всё отражается и отражается?
Вопрос: пусть у нас есть комната, ограниченная идеальными зеркалами. Можно ли там поставить точечный источник света так, чтобы в результате комната была освещена целиком? Или, может быть, свечку вообще можно ставить почти куда угодно — ведь свет всё отражается и отражается?
Victor Kleptsyn
М
12:36
Математические байки
Оказывается, что нет — и пример был опубликован в 1958 году отцом и сыном Пенроузами. Контрпример ко второму (более слабому вопросу) это вот такая фигура —
Victor Kleptsyn
М
12:38
Математические байки
Верхняя её часть это половина эллипса, а большая ось этого эллипса касается нижней части границы в фокусах — отсекая тем самым отмеченные A и B области.
Victor Kleptsyn
М
12:39
Математические байки
Как мы знаем, луч, вышедший из одного из фокусов, попадает в другой. Поэтому луч, вышедший из отрезка между фокусами (то есть из области A), вернётся тоже на отрезок между ними, уйдя обратно в область A: сравните с лучом, отражающимся в той же точке эллипса и приходящем из одного из фокусов.
Наоборот, луч, приходящий из области B, уйдёт тоже в область B (с другой стороны). Значит, где бы мы ни поставили свечку в области A, она не осветит ничего в области B.
Наоборот, луч, приходящий из области B, уйдёт тоже в область B (с другой стороны). Значит, где бы мы ни поставили свечку в области A, она не осветит ничего в области B.
Victor Kleptsyn
М
12:41
Математические байки
И для этого рассуждения используется только то, что происходит выше оси эллипса — области A и B ниже могут быть какой угодно формы.
Victor Kleptsyn
М
12:42
Математические байки
In reply to this message
(Справа на фото можно увидеть траекторию луча, стартовавшую из B — ниже оси она всегда приходит в B)
Victor Kleptsyn
М
12:42
Математические байки
Кстати, если запускать бильярд просто в эллипсе — то луч, продолжая отражаться, всегда будет касаться либо одного и того же софокусного эллипса (пересекая большую ось за фокусами), либо одной и той же софокусной гиперболы (пересекая ось между фокусами). Вот хорошая картинка (отсюда: https://mat-web.upc.edu/people/amadeu.delshams/articles/pebnonli.pdf ) —
Victor Kleptsyn
М
12:44
Математические байки
Но вернёмся к исходному вопросу. Пока мы увидели пример, показывающий, что если поставить свечку в область B, то не будет освещена область A, а если в A, то будет темно в области B. То есть куда угодно, и даже почти куда угодно, источник света ставить нельзя. Но ведь если свечку поставить совсем наверху, то оттуда-то мы сможем всё осветить, оттуда и A, и B видно!
Victor Kleptsyn
М
12:44
Математические байки
Давайте доработаем пример — возьмём две его копии, и соединим "туннелем" между областями A.
Victor Kleptsyn
М
12:46
Математические байки
Эту иллюстрацию я взял из "Математического дивертисмента" Фукса-Табачникова (который всячески рекомендую) —
Victor Kleptsyn
М
12:50
Математические байки
А вот — из видео Numberphile, где тоже много чего хорошего есть (кстати, в том видео рассказывает Howard Masur!), https://www.youtube.com/watch?v=xhj5er1k6GQ :
Victor Kleptsyn
М
12:51
Математические байки
Теперь уже у нас есть B-области и "сверху", и "снизу". И если свеча стоит в верхней полуплоскости — то мы не сможем осветить нижние B-области, а если в нижней — то верхние.
Victor Kleptsyn
М
12:55
Математические байки
Отдельно интересно было посмотреть, где и как пример был опубликован (кстати, смотреть первоисточники это вообще хороший рефлекс — и результат часто бывает интересный; как-нибудь я тут расскажу байку про "человек имеет форму шара"). А именно — вот ссылка:
Victor Kleptsyn
М
12:55
Математические байки
L. Penrose and R. Penrose, Puzzles for Christmas, New Scientist, 25 December (1958), 1580–1581, 1597.
Victor Kleptsyn
М
12:56
Математические байки
И это действительно "Puzzles" с ответами —
Victor Kleptsyn
М
12:56
Математические байки
И вот ответ —
Victor Kleptsyn
М
13:08
Математические байки
А головоломка по соседству — как Mr Tan может добраться до запутавшегося в ветвях воздушного змея:
Victor Kleptsyn
М
13:15
Математические байки
Возвращаясь к рассказу Элизы: а что, если бильярд многоугольный? Ведь отражение от прямого зеркала вещь гораздо более понятная.
Victor Kleptsyn
М
13:19
Математические байки
В 1995 году George Tokarsky придумал комнату, где, если поставить свечу в одной конкретной точке — некоторая другая точка не будет освещена. Более того, углы в ней все кратны 45 градусам.
Тут мне хочется процитировать коллег —
Тут мне хочется процитировать коллег —
Victor Kleptsyn
М
13:20
Математические байки
Н
Непрерывное математическое образование 16.09.2018 15:48:35
В многоугольной комнате с зеркальными стенами поставили точечный источник света. Обязательно ли вся комната освещена?
Примерно 40 лет это был открытый вопрос, а потом в 1995 году G.W.Tokarsky придумал комнату, для которой это не так.
Примерно 40 лет это был открытый вопрос, а потом в 1995 году G.W.Tokarsky придумал комнату, для которой это не так.
Victor Kleptsyn
М
М
13:22
Математические байки
Если, скажем, отразить всю комнату относительно самой правой стены, объединить, а стену убрать — то свеча в A0 не сможет осветить уже две точки, A1 и её зеркальный образ.
Victor Kleptsyn
М
13:28
Математические байки
Так вот — допустим, что у исходного многоугольника все углы рационально соизмеримы с развёрнутым (выражаются рациональным числом градусов, или имеют вид p/q * π в радианах).
Victor Kleptsyn
М
13:28
Математические байки
Тогда, как рассказывает Элиза (и Мазур в Numberphile), где бы ни находился точечный источник света, он осветит всю комнату, кроме, быть может, _конечного_ числа точек.
Victor Kleptsyn
М
13:36
Математические байки
И это утверждение следует из "теоремы о волшебной палочке" Эскина и Мирзахани (о которой Антон Зорич пишет тут — https://arxiv.org/abs/1502.05654 ) — но на этом пять минут Элизы истекли, и все пошли пить (традиционный) чай с плюшками.
Victor Kleptsyn
22 October 2019
М
13:17
Математические байки
In reply to this message
Давно обещанная последняя часть этой истории.
Есть классический вопрос в геометрии: сколько прямых пересекают четыре заданных попарно скрещивающихся прямых в пространстве?
И есть два совершенно разных подхода к нему.
Есть классический вопрос в геометрии: сколько прямых пересекают четыре заданных попарно скрещивающихся прямых в пространстве?
И есть два совершенно разных подхода к нему.
Victor Kleptsyn
М
13:18
Математические байки
Первый — геометрический.
Оставим из четырёх прямых только три, и спросим себя — как устроены те прямые, которые их все пересекают? И что заметает их объединение?
Оставим из четырёх прямых только три, и спросим себя — как устроены те прямые, которые их все пересекают? И что заметает их объединение?
Victor Kleptsyn
М
13:18
Математические байки
Ответ — нужно взять однополостный гиперболоид, на котором эти три прямые лежат. На однополостном гиперболоиде любая прямая одного семейства пересекает почти все прямые другого семейства — кроме одной, которой она параллельна (и которая получается симметрией относительно центра гиперболоида).
Victor Kleptsyn
М
13:18
Математические байки
А если ещё к пространству — и к гиперболоиду — добавить "бесконечно удалённые точки" (договорившись, что добавляется по одной точке для каждого направления, и что через эту точку проходят все параллельные прямые этого направления), то и вообще любая прямая одного семейства пересекает все прямые другого (просто одну — на бесконечности).
Victor Kleptsyn
М
13:19
Математические байки
А нет ли других прямых, которые данные три пересекают?
Нет: ведь три прямые l_1, l_2, l_3 не имеют общих точек (даже на бесконечности — они ведь скрещивающиеся!), значит, любая прямая l, которая их всех пересекает, имеет хотя бы три общих точки с гиперболоидом.
Нет: ведь три прямые l_1, l_2, l_3 не имеют общих точек (даже на бесконечности — они ведь скрещивающиеся!), значит, любая прямая l, которая их всех пересекает, имеет хотя бы три общих точки с гиперболоидом.
Victor Kleptsyn
М
13:19
Математические байки
А сам гиперболоид задаётся уравнением второго порядка. Ограничение которого на прямую — уравнение второго порядка с тремя различными корнями. То есть тождественный ноль.
Victor Kleptsyn
М
13:20
Математические байки
Значит, любая прямая, которая пересекает l_1,l_2,l_3, обязана лежать на проходящем через них гиперболоиде. (И значит, это прямая из второго семейства.)
Остаётся вернуться к вопросу про четыре прямых.
Остаётся вернуться к вопросу про четыре прямых.
Victor Kleptsyn
М
13:20
Математические байки
Пусть прямая l пересекает l_1,l_2,l_3,l_4; посмотрим, где может лежать точка пересечения P прямой l с l_4.
С одной стороны, P должна быть на гиперболоиде, проходящем через l_1,l_2,l_3 (потому что l лежит там целиком). С другой — P лежит на l_4 по определению.
С одной стороны, P должна быть на гиперболоиде, проходящем через l_1,l_2,l_3 (потому что l лежит там целиком). С другой — P лежит на l_4 по определению.
Victor Kleptsyn
М
13:21
Математические байки
Значит, P это точка пересечения l_4 с этим гиперболоидом.
И каждый вариант точки пересечения даёт свою прямую l. Вот и геометрический ответ — что есть столько прямых, в скольки точках l_4 пересекает соответствующий гиперболоид. Типичным образом их две, как корней у квадратного уравнения (ограничения уравнения гиперболоида на эту прямую) — но они могут комплексными.
И каждый вариант точки пересечения даёт свою прямую l. Вот и геометрический ответ — что есть столько прямых, в скольки точках l_4 пересекает соответствующий гиперболоид. Типичным образом их две, как корней у квадратного уравнения (ограничения уравнения гиперболоида на эту прямую) — но они могут комплексными.
Victor Kleptsyn
М
13:21
Математические байки
Второй подход — линейно-алгебраический; но для него мне сначала нужно будет сказать слова «проективная плоскость» и «проективное пространство». Заранее прошу прощения у тех, кто с ними уже хорошо знаком — несколько следующих сообщений можно пролистать, не читая.
Victor Kleptsyn
М
13:22
Математические байки
Решая геометрическую задачу и разбирая случаи, «а что, если эти две прямые не пересекаются, а параллельны», часто бывает удобно сказать, что две параллельные прямые «пересекаются на бесконечности». То есть формально добавить к плоскости «точки на бесконечности», в которых они пересекутся. Таких точек будет по одной на каждое направление; а все вместе они образуют бесконечно удалённую прямую. И когда такое добавление сделано — то, например, любые две различные прямые пересекаются ровно в одной точке. А пополненная плоскость называется проективной.
Victor Kleptsyn
М
13:23
Математические байки
Это хорошо, но неприятно, что точки теперь разделились на «конечные» и «на бесконечности»: в геометрии ведь хорошо то, что все точки равноправны. Так вот, оказывается, есть эквивалентное, но гораздо более «инвариантное» определение.
Victor Kleptsyn
М
13:23
Математические байки
А именно: точка проективной плоскости это, по определению, прямая в трёхмерном пространстве, проходящая через начало координат.
Victor Kleptsyn
М
13:23
Математические байки
Я помню, как когда-то на первом курсе меня это поразило — а сейчас, наоборот, кажется очень естественным. Ведь совершенно неважно, какие именно объекты выступают в качестве точек нашей геометрии, лишь бы аксиомы выполнялись. Пусть хоть слоны с крокодилами в зоопарке — лишь бы через любых двух крокодилов проходил ровно один слон.
Victor Kleptsyn
М
13:24
Математические байки
Давайте теперь свяжем эти два подхода. А именно: если мы теперь возьмём плоскость z=1. С одной стороны, это обычная плоскость с обычной геометрией в ней. С другой, большинство прямых через начало координат в R^3 её пересекут в единственной точке — и вот и соответствие между прямыми и точками на плоскости. А те прямые, что плоскости параллельны — и будут бесконечно удалёнными точками.
Victor Kleptsyn
М
13:25
Математические байки
(Иллюстрация отсюда —
https://www.mccme.ru/free-books/dubna/lvovski-developables.pdf )
https://www.mccme.ru/free-books/dubna/lvovski-developables.pdf )
Victor Kleptsyn
М
13:25
Математические байки
И дальше всё продолжается очень естественно. Что такое прямая в проективной геометрии? Это плоскость, проходящая через начало координат. И действительно, почти любая плоскость на плоскости z=1 высечет прямую — а единственная, что ей параллельна, это z=0, и это как раз бесконечно удалённая прямая.
Victor Kleptsyn
М
13:25
Математические байки
Две параллельные прямые (в плоскости z=1) действительно теперь (с точки зрения проективной геометрии) пересекаются в бесконечно удалённой точке — ибо соответствующие плоскости в R^3 пересекаются по прямой, параллельной им и проходящей через начало координат. А это и есть одна из бесконечно удалённых точек.
Victor Kleptsyn
М
13:26
Математические байки
Равноправие точек обеспечивается тем, что можно взять не плоскость z=1, а, к примеру, плоскость x=1 или y=1 (или вообще любую, не проходящую через ноль). И бесконечно удалёнными станут уже другие точки; правда, расстояния и углы такой переход не сохранит.
Victor Kleptsyn
М
13:26
Математические байки
Наконец, проективные преобразования плоскости получаются, если взять линейные преобразования пространства, и посмотреть, как они действуют на множестве прямых в R^3, проходящих через начало координат.
Victor Kleptsyn
М
13:26
Математические байки
Понятно, что это « проективная геометрия в двух словах » — а нормально её можно почитать, например, в Куранте-Робинсоне, см. главу 4: http://ilib.mccme.ru/pdf/kurant.pdf
Victor Kleptsyn
М
13:27
Математические байки
Так вот: давайте рассмотрим уже не проективную плоскость, а проективное пространство; точно так же, это множество прямых, проходящих через начало координат в R^4.
Прямая в проективном пространстве это плоскость в R^4. Две прямые скрещиваются, если соответствующие им плоскости пересекаются только по началу координат. И, наоборот, пересекаются, если у плоскостей есть нетривиальное пересечение.
Прямая в проективном пространстве это плоскость в R^4. Две прямые скрещиваются, если соответствующие им плоскости пересекаются только по началу координат. И, наоборот, пересекаются, если у плоскостей есть нетривиальное пересечение.
Victor Kleptsyn
М
13:27
Математические байки
А теперь перейдём к нашей задаче. У нас есть четыре попарно скрещивающиеся прямые в пространстве, то есть четыре плоскости в R^4, любые две из которых пересекаются лишь по началу координат. А до какой степени можно упростить эту картину?
Victor Kleptsyn
М
13:28
Математические байки
Возьмём первые две скрещивающиеся прямые — соответствующие им плоскости можно взять за координатные в R^4: пусть это будут Oxy и Ozt.
Victor Kleptsyn
М
13:29
Математические байки
А третью и четвёртую тогда можно рассматривать, как графики (обратимых) отображений из первой плоскости во вторую. В частности, заменой координат третью плоскость можно сделать « диагональной »: состоящей из векторов вида (u,u) для всех u из R^2. Ну а четвёртая это просто график какого-то линейного отображения.
Victor Kleptsyn
М
13:29
Математические байки
Итого: плоскости приведены к виду множеств всевозможных (u,0), (0,u), (u,u) и (u,Au) соответственно, где A — некоторое отображение.
Victor Kleptsyn
М
13:29
Математические байки
А что такое прямая, пересекающая эти четыре? Это плоскость π, нетривиально пересекающая все эти плоскости. Значит, в ней найдутся вектора вида (u,0) — раз она пересекает первую — и (0,v) — раз пересекает вторую.
Victor Kleptsyn
М
13:30
Математические байки
Тогда это её базис — то есть все вектора π имеют вид (au,bv). Но π должна пересекать третью — "диагональную" — плоскость, значит, там найдётся ненулевой вектор вида (au,bv), для которого au=bv. То есть v= (a/b)u, поэтому v можно заменить на u.
Victor Kleptsyn
М
13:30
Математические байки
Остаётся последнее — π должна пересекать и четвёртую плоскость. Значит, там найдётся вектор вида
(au,bu)=(au, A(au)).
(au,bu)=(au, A(au)).
Victor Kleptsyn
М
13:31
Математические байки
Если его сжать в a раз, то получится вектор
(u,(b/a)u) = (u, Au), и значит,
Au=cu, где c=b/a.
(u,(b/a)u) = (u, Au), и значит,
Au=cu, где c=b/a.
Victor Kleptsyn
М
13:32
Математические байки
То есть вектор u линейное преобразование A переводит в пропорциональный себе! А это и есть собственный вектор. Ура!
Victor Kleptsyn
М
13:32
Математические байки
Итак, прямые, пересекающие четыре данных, оказались соответствующими собственным векторам матрицы 2x2.
Да, в качестве рекламы — очень хорошая иллюстрация собственных векторов (для тех, кто с ними ещё не сталкивался) есть тут:
https://youtu.be/PFDu9oVAE-g?t=137
Да, в качестве рекламы — очень хорошая иллюстрация собственных векторов (для тех, кто с ними ещё не сталкивался) есть тут:
https://youtu.be/PFDu9oVAE-g?t=137
Victor Kleptsyn
М
13:33
Математические байки
А собственных векторов у типичной матрицы 2x2 как раз два — хотя иногда они (как и корни квадратного уравнения) бывают и комплексными.
Victor Kleptsyn
М
13:33
Математические байки
Вот мы и получили линейно-алгебраический взгляд на тот же вопрос!
Victor Kleptsyn
М
13:33
Математические байки
Соседний вопрос — а много ли « существенно различных » четвёрок попарно скрещивающихся прямых в пространстве? Если на них действовать проективными преобразованиями — то как будут устроены инварианты такого действия? Или, может быть, любую четвёрку можно перевести в любую (точно так же, как любую тройку можно перевести в любую даже аффинным преобразованием)?
Victor Kleptsyn
М
13:34
Математические байки
Если посчитать размерности, то сразу видно, что инварианты будут: прямая в R^3 задаётся (локально) 4 числами (например, 2 числа для её направления, задаваемого как точка на сфере, и ещё 2 на координату её пересечения с одной из координатных плоскостей, которой она не параллельна). Так что пространство (или, правильнее сказать, многообразие) четвёрок прямых 4*4=16-мерно.
Victor Kleptsyn
М
13:35
Математические байки
А проективное преобразование это (невырожденное) линейное преобразование R^4 (задающееся 16-ю элементами своей матрицы) — с точностью до умножения на константу (ибо гомотетия прямые не меняет). Поэтому группа проективных преобразований проективного пространства 16-1=15-мерна.
Victor Kleptsyn
М
13:35
Математические байки
15<16, так что минимум один инвариант будет.
Victor Kleptsyn
М
13:35
Математические байки
Так вот, инвариантов на самом деле два (что означает, что у типичной конфигурации есть одномерный стабилизатор — одномерная подгруппа преобразований, которая её оставляет на месте).
Victor Kleptsyn
М
13:35
Математические байки
На геометрическом языке: есть две прямые, пересекающие нашу четвёрку. На каждой из этих прямых есть четыре точки пересечения. А у четырёх точек есть — двойное отношение! И вот два инвариантных числа.
Victor Kleptsyn
М
13:36
Математические байки
На языке линейной алгебры: когда у нас есть четыре плоскости в R^4, то третью и четвёртую можно рассматривать, как графики отображений из первой во вторую. А тогда их композиционное частное — корректно определённое отображение из первой плоскости в себя. Это, конечно, та самая матрица A выше — просто можно сказать « композиционное частное », а можно — « выбор координат на плоскостях, при котором одно из отображений тождественно ».
Victor Kleptsyn
М
13:36
Математические байки
И отображение A корректно определено — а тогда у него есть инварианты: собственные значения.
Victor Kleptsyn
М
13:36
Математические байки
Так вот, эти два ответа совпадают — двойные отношения точек пересечения как раз и есть собственные значения матрицы A.
Victor Kleptsyn
М
13:38
Математические байки
Более того, в каком-то смысле мне такой подход кажется правильным объяснением того, почему двойное отношение четырёх точек инвариантно относительно проективных преобразований. Можно это, конечно, аккуратно проверять — а можно сказать, что если мы рассмотрим на плоскости четыре прямых через начало координат, и у нас есть только линейная структура, то третья и четвёртая прямые это графики отображения из первой во вторую. А тогда можно взять их композиционное частное — которое будет линейным преобразованием прямой. То есть умножением на константу. И эта константа — инвариант преобразований, которые линейную структуру сохраняют.
Victor Kleptsyn
М
13:39
Математические байки
А с другой стороны, она и есть двойное отношение, что проверяется совсем мгновенно. Пусть у нас есть прямая, не проходящая через начало координат O, и она пересекает наши четыре прямые в точках A,B,C,D. Если отрезки OA и OB на первой и второй прямых взять за единичные, то прямая OC будет графиком функции умножения на (AC:CB). А прямая OD — умножения на (AD:DB). А их композиционное частное — на частное этих отношений. То есть на двойное отношение.
Victor Kleptsyn
М
13:41
Математические байки
Кстати — бывают ведь ещё нетипичные случаи. Если матрица A оказывается скалярной, это означает, что каждый вектор для неё собственный. И это значит, что все четыре прямые лежат на одном гиперболоиде.
Victor Kleptsyn
М
13:42
Математические байки
А если преобразование A это жорданова клетка — матрица вида (c, 1 \\ 0, c) — то собственный вектор у него только один. И это отвечает случаю, когда четвёртая прямая касается гиперболоида (но не лежит на нём).
Victor Kleptsyn
М
13:44
Математические байки
И из этой конфигурации можно сделать такую забавную задачу: пусть в пространстве заданы четыре попарно скрещивающиеся прямые, и пусть одна из них касается гиперболоида, проходящего через три другие, но не лежит на нём. Докажите, что тогда _любая_ из этих прямых касается гиперболоида, проходящего через три другие.
Victor Kleptsyn
М
13:50
Математические байки
Вот такой сюжет; ну и на этом я на сегодня хочу прекратить дозволенные речи.
Victor Kleptsyn
31 October 2019
М
12:58
Математические байки
Две короткие истории про "как посчитать".
Victor Kleptsyn
М
12:58
Математические байки
Допустим, мы хотим диагонализовать матрицу A размера 2x2 — и ищем её собственные вектора.
Victor Kleptsyn
М
12:58
Математические байки
Вот мы нашли собственные значения, λ_1 и λ_2...
... и собираемся решить две системы, чтобы найти собственные вектора. А надо ли это делать?
... и собираемся решить две системы, чтобы найти собственные вектора. А надо ли это делать?
Victor Kleptsyn
М
12:59
Математические байки
Нет!
Ведь (A-λ_1*Id)(A-λ_2*Id)=0 (aka теорема Гамильтона-Кэли).
Ведь (A-λ_1*Id)(A-λ_2*Id)=0 (aka теорема Гамильтона-Кэли).
Victor Kleptsyn
М
12:59
Математические байки
Значит, собственный вектор с собственным значением λ_1 можно прочитать в (любом) столбце матрицы A-λ_2*Id. И наоборот, собственный вектор с собственным значением λ_2 — в любом столбце матрицы A-λ_1*Id.
Victor Kleptsyn
М
13:00
Математические байки
С матрицами 3x3 такое тоже можно применять, но тут уже вопрос, что кому проще: перемножить две матрицы (A-λ_1*Id)(A-λ_2*Id), чтобы в столбце прочитать собственный вектор, или решить систему (A-λ_3*Id) v =0.
(Помнится, этому трюку нас в своё время научил И. А. Дынников. Давно это было!)
(Помнится, этому трюку нас в своё время научил И. А. Дынников. Давно это было!)
Victor Kleptsyn
М
13:01
Математические байки
Второй трюк — а что, если мы хотим посчитать какую-то функцию от матрицы (скажем, сотую степень, или экспоненту) в исходном базисе. И матрица опять маленькая, 2x2 или 3x3.
Victor Kleptsyn
М
13:02
Математические байки
Можно, конечно, найдя собственные значения, найти потом собственные вектора, вычислить функцию в собственном базисе (допустим, все собственные значения некратные — так что матрица диагонализуется — и тогда просто поэлементно применить к собственным значениям на диагонали), потом вернуться в исходный (включая обращение матрицы перехода и умножение матриц)...
Victor Kleptsyn
М
13:03
Математические байки
Но можно — проще!
Пусть мы хотим найти F(A), где F — многочлен.
Пусть мы хотим найти F(A), где F — многочлен.
Victor Kleptsyn
М
13:03
Математические байки
Поделим F(x) с остатком на характеристический многочлен P(x)=П_j (x-λ_j) матрицы A:
F(x)=P(x)Q(x)+R(x).
Но P(A)=0 (опять теорема Гамильтона-Кэли), значит, F(A)=R(A).
F(x)=P(x)Q(x)+R(x).
Но P(A)=0 (опять теорема Гамильтона-Кэли), значит, F(A)=R(A).
Victor Kleptsyn
М
13:05
Математические байки
При этом остаток R(x) — штука "простая"; скажем, для матрицы размера 2x2 это просто линейный многочлен, R(x)=ax+b, и
F(A)=R(A)=a*A+b*Id.
F(A)=R(A)=a*A+b*Id.
Victor Kleptsyn
М
13:05
Математические байки
Для матрицы 3x3 — многочлен второй степени, так что R(A) посчитать тоже не очень сложно, знать бы только R(x) как многочлен. Но вот как его найти?
Victor Kleptsyn
М
13:06
Математические байки
А очень просто: если мы делим многочлен F с остатком на P, то значения остатка в корнях P совпадают со значениями F.
Victor Kleptsyn
М
13:08
Математические байки
Поэтому остаток от деления F на P с некратными корнями — это единственный многочлен степени <= deg P -1, у которого в корнях те же значения, что и у F.
Victor Kleptsyn
М
13:08
Математические байки
Иными словами — интерполяционный многочлен Лагранжа.
Victor Kleptsyn
М
13:13
Математические байки
И вот получается алгоритм вычисления F(A): сначала построить интеполяционный многочлен R(x) по известным значениям F(λ_j) в корнях P(x) — собственных значениях λ_j. И потом подставить туда A.
Для матрицы A размера 2x2, нахождение R(x) это проведение прямой по двум точкам, что совсем быстро.
Для матрицы A размера 2x2, нахождение R(x) это проведение прямой по двум точкам, что совсем быстро.
Victor Kleptsyn
М
13:14
Математические байки
Для матрицы размера 3x3 — работы чуть больше (возвести A в квадрат, найти квадратный трёхчлен по трём значениям), но тоже вполне обозримо.
Victor Kleptsyn
М
13:18
Математические байки
А узнал я это в своё время из посвящённого многочленам Лагранжа курса Аскольда Георгиевича Хованского — https://www.mccme.ru/dubna/2006/courses/khovansky.html (а вот тут лежат его записки — https://www.mccme.ru/dubna/2006/notes/newlagrang.pdf )
Victor Kleptsyn
7 November 2019
М
20:27
Математические байки
Математические постеры, которые висят в коридорах факультета математики (https://math.u-bourgogne.fr/ ) в Дижоне:
Victor Kleptsyn
М
20:29
Математические байки
Не у всех есть глубокое содержание — но смотрятся очень хорошо (и "создают атмосферу").
Victor Kleptsyn
М
20:30
Математические байки
In reply to this message
Тут — стереографическая проекция, и это один из кадров из второй главы фильма Жиса, Йоса и Альвареса "Измерения":
http://dimensions-math.org/Dim_RU.htm
http://dimensions-math.org/Dim_RU.htm
Victor Kleptsyn
М
20:33
Математические байки
Начинается он довольно просто — но потом доходит до правильных многогранников в размерности 4, и до того, как на них можно "посмотреть глазами": сначала "надуть", чтобы они легли на трёхмерную сферу в R^4, а потом сделать стереографическую проекцию, получив картинку в R^3.
Victor Kleptsyn
М
20:38
Математические байки
И про расслоение Хопфа и окружности Вилларсо в конце тоже рассказывают. Я, собственно, ровно оттуда узнал, что если рассечь тор, полученный честным вращением окружности, бикасательной плоскостью —
Victor Kleptsyn
М
20:39
Математические байки
то в сечении получатся две пересекающиеся окружности:
Victor Kleptsyn
М
20:40
Математические байки
Так что на "торе вращения" есть _четыре_ семейства окружностей: параллели, меридианы, и два семейства окружностей Вилларсо.
Victor Kleptsyn
М
20:47
Математические байки
In reply to this message
Возвращаясь к правильным многогранникам — вот картинки одного из них, 120-гранника:
Victor Kleptsyn
М
20:50
Математические байки
Собственно, построить проще двойственный к нему, многогранник со 120 вершинами (и 600 гранями). А именно — если взять додекаэдр, то группа его вращений состоит из 60 элементов (любую грань в любую 12 способами, и самосовмещений грани 5 штук, 12*5=60).
Victor Kleptsyn
М
20:51
Математические байки
Кстати, это группа A_5 — и если задаться вопросом, "а почему именно группа перестановок, кого она переставляет", то на него есть удивительно хороший ответ: 5 вписанных кубов.
Victor Kleptsyn
М
20:52
Математические байки
Точно так же, как четыре вершины куба, соседние по диагонали в каждой грани, образуют два правильных тетраэдра — из вершин додекаэдра можно составить пять разных кубов.
Victor Kleptsyn
М
20:53
Математические байки
Рёбра куба в любой грани додекаэдра будут диагоналями — и любая диагональ однозначно достраивается до куба.
Victor Kleptsyn
М
20:54
Математические байки
И вот эти-то пять кубов группа вращений додекаэдра и переставляет.
Victor Kleptsyn
М
20:56
Математические байки
In reply to this message
Так вот — группа вращений додекаэдра состоит из 60 элементов. А группа SO(3) вращений трёхмерного пространства двулистно накрывается группой кватернионов единичной длины (трёхмерное пространство рассматривается как чисто мнимые кватернионы, а сопряжение z->q z q^{-1} сохраняет длины и вещественную ось, значит, оказывается его вращением).
Victor Kleptsyn
М
20:57
Математические байки
Группа кватернионов единичной длины это трёхмерная сфера в H=R^4 — и прообраз группы из 60 элементов это 120 её точек, которые и будут вершинами того самого правильного многогранника.
Victor Kleptsyn
М
21:06
Математические байки
А вообще, о том, как классифицируются все правильные многогранники, рассказано в дубнинской брошюре Е. Смирнова — https://www.mccme.ru/free-books/dubna/smirnov-reflections-v2.pdf .
Собственно, классифицируется-то больше: та же система корней E_8 вещь более важная, чем знание о том, что в размерности выше 4 правильные многогранники только стандартные ("[гипер]тетраэдр", "[гипер]куб" и "[гипер]октаэдр" = "двойственный к [гипер]кубу").
Собственно, классифицируется-то больше: та же система корней E_8 вещь более важная, чем знание о том, что в размерности выше 4 правильные многогранники только стандартные ("[гипер]тетраэдр", "[гипер]куб" и "[гипер]октаэдр" = "двойственный к [гипер]кубу").
Victor Kleptsyn
М
21:07
Математические байки
Иллюстрация оттуда, объясняющая, при чём тут группы отражений —
Victor Kleptsyn
М
21:08
Математические байки
И её "живой аналог" для икосаэдра (за который спасибо М. Панову) —
Victor Kleptsyn
М
21:09
Математические байки
(Группа отражений тут чуть меньшая — все зеркала идут по рёбрам — но зато смотрится более красиво и симметрично.)
Victor Kleptsyn
М
21:11
Математические байки
А отражения собраны из одного-единственного исходного треугольника — собственно, как тут:
http://www.etudes.ru/ru/models/football-mirror-icosahedron/
http://www.etudes.ru/ru/models/football-mirror-icosahedron/
Victor Kleptsyn
М
21:15
Математические байки
In reply to this message
А картинка на этом постере соответствует вот этой статье —
http://www.ams.org/publicoutreach/feature-column/fcarc-lorenz
http://www.ams.org/publicoutreach/feature-column/fcarc-lorenz
Victor Kleptsyn
М
21:19
Математические байки
Заслуживающей отдельного рассказа самой по себе – чего стоят одни ролики анимаций, которые к ней "прикручены".
Victor Kleptsyn
М
21:28
Математические байки
Но это будет как-нибудь в другой раз — тут есть красивый рассказ про то, почему пространство решёток на комплексной плоскости это C^2 без кривой {z^2=w^3}, что эта кривая высекает на единичной сфере узел-трилистник, и это именно тот самый трилистник, который появляется на постере, что фундаментальная группа дополнения к нему это группа кос B_3, потому что корни кубического уравнения, и так далее — но это надо писать вдумчиво, так что как-нибудь в другой раз.
Victor Kleptsyn
М
21:31
Математические байки
А чтобы завершить вечер картинок — фреска в UMPA ENS Lyon:
Victor Kleptsyn
М
21:31
Математические байки
Она большая, во всю стену (так что слева на фотографии — это дверь), и с кучей математических сюжетов.
Victor Kleptsyn
М
21:32
Математические байки
Правильные многогранники и (двоичные?) деревья, конечно, бросаются в глаза.
Victor Kleptsyn
М
21:33
Математические байки
А вот что воздушный шар раскрашен под расслоение Хопфа — уже нужно заметить.
Victor Kleptsyn
М
21:48
Математические байки
Солнце (которое, правда, не очень видно) раскрашено под универсальную накрывающую сферы Римана без трёх точек — которая есть диск (а треугольники "с вершинами на абсолюте" переходят в верхнюю и нижнюю полуплоскости, в зависимости от раскраски).
Лента справа завивается дорожкой вихрей Кармана — https://en.wikipedia.org/wiki/K%C3%A1rm%C3%A1n_vortex_street .
А верёвка завязывается в дикий узел (https://en.wikipedia.org/wiki/Wild_knot )
Лента справа завивается дорожкой вихрей Кармана — https://en.wikipedia.org/wiki/K%C3%A1rm%C3%A1n_vortex_street .
А верёвка завязывается в дикий узел (https://en.wikipedia.org/wiki/Wild_knot )
Victor Kleptsyn
М
21:49
Математические байки
Ну и последнее на сегодня — а вот эти постеры висят у нас в Ренне на лестнице:
http://sorciersdesalem.math.cnrs.fr/Posters/posters.html
http://sorciersdesalem.math.cnrs.fr/Posters/posters.html
Victor Kleptsyn
М
21:50
Математические байки
Там сильно больше комментариев — правда, они по-французски...
Victor Kleptsyn
М
21:51
Математические байки
Ну и на этом я рассказ "о красивых картинках", наверное, завершу.
Victor Kleptsyn
8 November 2019
М
14:02
Математические байки
В продолжение темы про узлы — байка про трёхцветные раскраски.
Victor Kleptsyn
М
14:02
Математические байки
Как можно доказывать, что узел (формально, вложение окружности в R^3) нельзя развязать? Или что два узла различны?
Victor Kleptsyn
М
14:03
Математические байки
Самый естественный подход — нужен какой-нибудь инвариант. И почти всегда инвариант строится не по узлу в R^3, а по его диаграмме — "узлу, вид сверху".
Victor Kleptsyn
М
14:03
Математические байки
Вот взятая из Википедии таблица узлов с небольшим числом перекрёстков:
Victor Kleptsyn
М
14:04
Математические байки
Так вот, самый простой в определении инвариант — это число правильных трёхцветных раскрасок.
Victor Kleptsyn
М
14:05
Математические байки
А именно, раскрасим диаграмму узла в три цвета (красный, синий, зелёный) — раскрашивая каждую связную компоненту (от одного ныряния "под" перекрёсток до другого) в один цвет.
Определение: раскраска называется правильной, если для каждого перекрёстка (в котором встречаются две "ныряющие вниз" компоненты и одна, проходящая поверху) мы в нём видим либо все три цвета, либо только один.
Определение: раскраска называется правильной, если для каждого перекрёстка (в котором встречаются две "ныряющие вниз" компоненты и одна, проходящая поверху) мы в нём видим либо все три цвета, либо только один.
Victor Kleptsyn
М
14:05
Математические байки
Пример: правильная раскраска трилистника (image credit: Wikipedia)
Victor Kleptsyn
М
14:07
Математические байки
Теорема. Число правильных раскрасок — инвариант узла.
Victor Kleptsyn
М
14:07
Математические байки
Как такое нужно доказывать? Как обычно: показывать, что в процессе перехода от одного узла к другому он не меняется.
Victor Kleptsyn
М
14:08
Математические байки
Процесс деформации (гомотопии) одного узла в другой с точки зрения диаграмм разбивается на конечное число _движений Редемейстера_:
Victor Kleptsyn
М
14:09
Математические байки
(image credit: Wolfram Mathworld, http://mathworld.wolfram.com/ReidemeisterMoves.html )
Victor Kleptsyn
М
14:09
Математические байки
Соответственно, нужно доказать, что каждое такое движение не изменяет числа трёхцветных раскрасок.
Victor Kleptsyn
М
14:09
Математические байки
Как нас учат специалисты по комбинаторике, лучше всего равенство натуральных чисел доказывается биекцией. Так вот — между трёхцветными раскрасками есть биекция, сохраняющая раскраску вне перестраиваемой области (а легко видеть, что внутрь области перестройки раскраска всегда продолжается не более чем одним способом).
Victor Kleptsyn
М
14:10
Математические байки
Например:
Victor Kleptsyn
М
14:11
Математические байки
Правда, проверять такое утверждение напрямую грустно: нужно для всех возможных наборов входящих снаружи цветов проверить, что либо одновременно внутрь продолжится, либо не продолжится, и это довольно много вариантов.
Victor Kleptsyn
М
14:12
Математические байки
Ну или нужно сказать, что при данных цветах сверху, продолжая через картинку, мы и в том, и в другом случае получим всегда одни и те же цвета снизу — что уже более разумно, но всё ещё остаётся каким-то странным перебором.
Victor Kleptsyn
М
14:12
Математические байки
И тут помогает вот какое наблюдение: обозначим наши цвета 0, 1 и 2. Три цвета удовлетворяют условию "все одинаковые или все разные" тогда или только тогда, когда их сумма равна 0 mod 3.
Victor Kleptsyn
М
14:13
Математические байки
Действительно, 0+1+2=0 mod 3, 3x=0 mod 3.
Victor Kleptsyn
М
14:13
Математические байки
(А третий цвет однозначно определяется двумя, так что переход в обратную сторону тоже мгновенный)
Victor Kleptsyn
М
14:13
Математические байки
Соответственно, мы можем работать в поле по модулю 3 — зная, что если два из подошедших к перекрёстку цветов это a и b, то третий это -(a+b).
Victor Kleptsyn
М
14:14
Математические байки
In reply to this message
И теперь уже мгновенно проверяется, что если три подходящих к R3-перестройке сверху (на рисунке выше) цвета это a, b и c (слева направо), то вниз они придут и в том, и в другом случае как
-a+b+c, b и -(a+b).
-a+b+c, b и -(a+b).
Victor Kleptsyn
М
14:15
Математические байки
А проверить движения R1 и R2 ещё быстрее.
Victor Kleptsyn
М
14:16
Математические байки
Правда, всё равно остаётся ощущение чуда: почему именно при таких правилах получился инвариант?
Victor Kleptsyn
М
14:16
Математические байки
Оказывается, на это есть хороший ответ — но прежде ещё пара замечаний.
Во-первых, мы между делом обнаружили, что число правильных трёхцветных раскрасок всегда будет степенью тройки. Потому что это число решений системы линейных (однородных) уравнений вида x_i+x_j+x_k=0 (где i,j и k — номера нитей, встречающихся в данном перекрёстке) над полем из трёх элементов.
Во-первых, мы между делом обнаружили, что число правильных трёхцветных раскрасок всегда будет степенью тройки. Потому что это число решений системы линейных (однородных) уравнений вида x_i+x_j+x_k=0 (где i,j и k — номера нитей, встречающихся в данном перекрёстке) над полем из трёх элементов.
Victor Kleptsyn
М
14:17
Математические байки
А это 3 в степени размерность пространства решений.
Victor Kleptsyn
М
14:17
Математические байки
Во-вторых, условие "три одинаковых или три разных" встречается ещё в замечательной игре SET:
Victor Kleptsyn
М
14:18
Математические байки
Там нужно находить (из выложенных на стол 12) тройки карточек, по каждому из четырёх параметров (цвет, тип закраски, количество, форма) либо все совпадающие, либо все различающиеся. И из-за перевода выше это можно переформулировать как поиск прямых в четырёхмерном пространстве над полем из трёх элементов.
Не то, чтобы это сильно в игре помогало. :)
Не то, чтобы это сильно в игре помогало. :)
Victor Kleptsyn
М
14:19
Математические байки
Так вот — а _почему_ число трёхцветных раскрасок это инвариант?
Оказывается, что хоть мы на него смотрели "аддитивно", на него есть и "некоммутативный" взгляд.
Оказывается, что хоть мы на него смотрели "аддитивно", на него есть и "некоммутативный" взгляд.
Victor Kleptsyn
М
14:25
Математические байки
У узла есть такой естественный инвариант: фундаментальная группа дополнения к нему (https://en.wikipedia.org/wiki/Knot_group )
Victor Kleptsyn
М
14:25
Математические байки
То есть группа петель в R^3\K, в которой произведение это последовательный проход сначала одной петли, потом другой.
Victor Kleptsyn
М
14:27
Математические байки
Если узел "сплющить" до диаграммы почти-в-плоскости, то очень естественно поставить отмеченную точку, в которой петли начинаются и заканчиваются, на бесконечности над этой плоскостью.
Тогда легко увидеть, что фундаментальная группа порождается петлями вида "спустились к диаграмме, обошли вокруг одной из нитей, поднялись обратно":
Тогда легко увидеть, что фундаментальная группа порождается петлями вида "спустились к диаграмме, обошли вокруг одной из нитей, поднялись обратно":
Victor Kleptsyn
М
14:29
Математические байки
А соотношения приходят из перекрёстков: два обхода "нижних" нитей перекрёстка сопрягаются обходом верхней нити:
Victor Kleptsyn
М
14:31
Математические байки
На этом рисунке γ_j=γ_i^{-1} γ_k γ_i:
спускаясь в южный квадрант, мы уходим не сразу в западный, а сначала в восточный (это γ_i), потом в верхний (γ_k), и наконец, в восточный (γ_i^{-1}).
спускаясь в южный квадрант, мы уходим не сразу в западный, а сначала в восточный (это γ_i), потом в верхний (γ_k), и наконец, в восточный (γ_i^{-1}).
Victor Kleptsyn
М
14:33
Математические байки
Так вот: раз фундаментальная группа G=π_1(R^3\K) это инвариант, то инвариант и всё, что по ней можно построить.
Давайте посчитаем число гомоморфизмов из G в группу перестановок S_3 трёх элементов — но не любых, а таких, чтобы петля-один обход нити переходила бы в транспозицию. (Поскольку все такие обходы сопряжены, то это тоже инвариантное условие.)
Давайте посчитаем число гомоморфизмов из G в группу перестановок S_3 трёх элементов — но не любых, а таких, чтобы петля-один обход нити переходила бы в транспозицию. (Поскольку все такие обходы сопряжены, то это тоже инвариантное условие.)
Victor Kleptsyn
М
14:35
Математические байки
В S_3 есть три транспозиции: (12), (13) и (23).
Victor Kleptsyn
М
14:36
Математические байки
И это и будут наши три цвета: ведь условие "a^{-1} b a = c" для транспозиций a,b,c из S_3 равносильно условию "либо все три совпадают, либо все три различны".
Victor Kleptsyn
М
14:38
Математические байки
Вот, собственно, и всё — условие на правильность раскраски оказалось условием на гомоморфизм фундаментальной группы в S_3 (что соотношения выполняются). И число правильных раскрасок — это число вот таких гомоморфизмов.
Victor Kleptsyn
М
14:43
Математические байки
Последний комментарий в виде ассоциации — шестая задача отсюда:
http://math.mosolymp.ru/upload/files/2017/khamovniki/10-1/2016.09.26_Vesa.pdf
http://math.mosolymp.ru/upload/files/2017/khamovniki/10-1/2016.09.26_Vesa.pdf
Victor Kleptsyn
М
14:44
Математические байки
(Не буду объяснять, почему, будет подсказка, но если что, рядом лежат и решения: via http://math.mosolymp.ru/2017_khamovniki_10_1 )
Victor Kleptsyn
М
14:46
Математические байки
И на этом севшая батарея ноутбука намекает, что пора на сегодня прекратить дозволенные речи.
Victor Kleptsyn
15 November 2019
М
19:27
Математические байки
Вообще-то я собирался рассказывать про другое, но вчерашний доклад Микеле Триестино поменял мои планы:
Victor Kleptsyn
М
19:28
Математические байки
Рассмотрим вот такую группу:
H_4=< a,b,c,d | aba^{-1}=b^2,
bcb^{-1}=c^2,
cdc^{-1}=d^2,
dad^{-1}=a^2 >
H_4=< a,b,c,d | aba^{-1}=b^2,
bcb^{-1}=c^2,
cdc^{-1}=d^2,
dad^{-1}=a^2 >
Victor Kleptsyn
М
19:28
Математические байки
Собственно, индекс 4 подсказывает, что есть и группа H_n. У неё n образующих — a_1,...,a_n — и n соотношений:
a_i a_{i+1} a_i^{-1} = a_{i+1}^2.
a_i a_{i+1} a_i^{-1} = a_{i+1}^2.
Victor Kleptsyn
М
19:30
Математические байки
Просто группы H_2 и H_3 оказываются тривиальны — а вот группа H_4 уже бесконечна. Что, впрочем, неочевидно, но пока мы в это поверим.
Так вот, с помощью этой группы Хигман в 1951-м построил первый пример бесконечной конечно-порождённой простой группы.
Так вот, с помощью этой группы Хигман в 1951-м построил первый пример бесконечной конечно-порождённой простой группы.
Victor Kleptsyn
М
19:31
Математические байки
А именно, оказывается, что верно вот такое утверждение —
Victor Kleptsyn
М
19:31
Математические байки
Теорема (Хигман, 1951): у группы H_n нет нетривиальных конечных факторов.
Victor Kleptsyn
М
19:31
Математические байки
Забавным образом, эта теорема выводится из малой теоремы Ферма.
Victor Kleptsyn
М
19:32
Математические байки
А именно: пусть у нас есть какой-то конечный фактор фактор одной из групп H_n. Он порождён образами b_i образующих a_i. Давайте докажем, что они все тривиальны.
Victor Kleptsyn
М
19:32
Математические байки
Собственно, раз это фактор — на b_i выполнены те же соотношения, что и раньше на a_i, но в дополнение к ним и ещё какие-то.
Victor Kleptsyn
М
19:32
Математические байки
Во-первых, если тривиален хотя бы один образ b_i, то тривиальны они все — потому что b_i сопрягает b_{i+1} с его квадратом; раз b_i=e, то сопряжение ничего не делает, и b_{i+1}=b_{i+1}^2, и тогда b_{i+1}=e.
Victor Kleptsyn
М
19:33
Математические байки
Во-вторых, пусть теперь они все нетривиальны. Раз мы предположили, что фактор конечный, то это всё — элементы конечного порядка.
То есть у каждого b_i есть свой порядок m_i>1.
То есть у каждого b_i есть свой порядок m_i>1.
Victor Kleptsyn
М
19:33
Математические байки
Мы знаем, что b_i сопрягает b_{i+1} с его квадратом, b_{i+1}^2.
Применив это m_i раз, получаем, что b_{i+1} совпадает со своей 2^{m_i}-й степенью:
Применив это m_i раз, получаем, что b_{i+1} совпадает со своей 2^{m_i}-й степенью:
Victor Kleptsyn
М
М
19:34
Математические байки
То есть
b_{i+1}^{2^{m_i} - 1} = e,
откуда 2^{m_i} - 1 делится на m_{i+1}.
b_{i+1}^{2^{m_i} - 1} = e,
откуда 2^{m_i} - 1 делится на m_{i+1}.
Victor Kleptsyn
М
19:35
Математические байки
Значит, у нас есть n "стоящих по кругу" порядков m_i, и следующий является делителем 2 в степени предыдущий минус один.
Victor Kleptsyn
М
19:35
Математические байки
Остаётся заметить, что из малой теоремы Ферма следует вот такая лемма:
Лемма. Для любого m>1 наименьший простой делитель 2^m-1 строго больше наименьшего простого делителя m.
Лемма. Для любого m>1 наименьший простой делитель 2^m-1 строго больше наименьшего простого делителя m.
Victor Kleptsyn
М
М
19:36
Математические байки
(Это — из исходного текста Хигмана)
Victor Kleptsyn
М
19:36
Математические байки
Доказательство. Пусть r — наименьший простой делитель 2^m - 1.
Victor Kleptsyn
М
19:36
Математические байки
Тогда по малой теореме Ферма 2^{r-1} сравнимо с 1 по модулю r, и значит (алгоритм Евклида), 2^{НОД(m,r-1)} тоже сравнимо с 1 по модулю r.
Victor Kleptsyn
М
19:37
Математические байки
Если r не строго больше наименьшего простого делителя m, то m и r-1 взаимно просты, то есть НОД выше равен 1. И тогда 2=1 по модулю r => противоречие.
Victor Kleptsyn
М
19:37
Математические байки
Лемма доказана — а теорема из неё выводится мгновенно.
Потому что из неё следует, что у порядков m_i наименьшие простые делители строго возрастают. Но индексы i идут "по кругу" (по модулю n) — а возрастающая последовательность чисел замкнуться не может.
Потому что из неё следует, что у порядков m_i наименьшие простые делители строго возрастают. Но индексы i идут "по кругу" (по модулю n) — а возрастающая последовательность чисел замкнуться не может.
Victor Kleptsyn
М
19:38
Математические байки
Вот мы и получили противоречие — и тем самым доказали, что у H_n нет нетривиальных конечных факторов.
Victor Kleptsyn
М
М
19:38
Математические байки
Остаётся из неё получить простую бесконечную группу.
Victor Kleptsyn
М
19:39
Математические байки
Рассмотрим нормальные подгруппы H_4, не совпадающие с самой H_4. Как минимум одна такая есть — это просто {e}.
Victor Kleptsyn
М
19:40
Математические байки
Возьмём максимальную по включению такую подгруппу G. Такая есть; это можно увидеть стандартной техникой, через лемму Цорна — у любой "башни" вложенных нормальных подгрупп есть "супремум": объединение их всех.
Это тоже нормальная подгруппа, и тоже меньшая H_4 (если она совпадает с H_4, то в неё входят все 4 образующих a,b,c,d — а тогда они входят уже в какую-то из объединяемых подгрупп, противоречие). Значит, есть "максимальный" элемент — искомая максимальная нормальная подгруппа.
(Собственно, точно так же доказывается наличие базиса Гамеля в бесконечномерном линейном пространстве, и так далее — https://ru.wikipedia.org/wiki/Лемма_Цорна )
Это тоже нормальная подгруппа, и тоже меньшая H_4 (если она совпадает с H_4, то в неё входят все 4 образующих a,b,c,d — а тогда они входят уже в какую-то из объединяемых подгрупп, противоречие). Значит, есть "максимальный" элемент — искомая максимальная нормальная подгруппа.
(Собственно, точно так же доказывается наличие базиса Гамеля в бесконечномерном линейном пространстве, и так далее — https://ru.wikipedia.org/wiki/Лемма_Цорна )
Victor Kleptsyn
М
19:42
Математические байки
Но можно и совсем "вручную": перенумеровать элементы группы, начать с подгруппы {e}, и для каждого очередного элемента g_k из H_4 смотреть, можно ли его добавить в уже построенную подгруппу так, чтобы она (после добавления всех сопряжённых/обратных/степеней, чтобы остаться нормальной подгруппой) не стала H_4. Если можем — добавляем, нет — оставляем. То, что получится, когда мы пробежим всё H_4 (формально — объединение возрастающей башни подгрупп) и будет искомой.
Victor Kleptsyn
М
19:45
Математические байки
(Вопрос о том, можно ли тут совсем по-честному обойтись без аксиомы выбора, — учитывая, что процедура на каждом шагу однозначная, и совершаем мы только однократный выбор перечисления элементов H_4 — я собираюсь замести под ковёр, ибо речь сейчас не об этом.)
Victor Kleptsyn
М
19:46
Математические байки
Так вот — возьмём (какую-нибудь) максимальную по включению, меньшую H_4, нормальную подгруппу G в группе H_4.
И рассмотрим фактор H_4/G. Это и есть обещанный исторически первый пример бесконечной конечно-порождённой простой группы.
И рассмотрим фактор H_4/G. Это и есть обещанный исторически первый пример бесконечной конечно-порождённой простой группы.
Victor Kleptsyn
М
19:46
Математические байки
Действительно, во-первых, это бесконечная группа, потому что у H_4 нет конечных факторов.
Во-вторых, она простая: если бы у неё была бы нетривиальная нормальная подгруппа, то её прообраз при факторизации H_4 -> H_4 / G был бы нормальной подгруппой H_4, большей G, а мы предположили, что G максимальная.
Во-вторых, она простая: если бы у неё была бы нетривиальная нормальная подгруппа, то её прообраз при факторизации H_4 -> H_4 / G был бы нормальной подгруппой H_4, большей G, а мы предположили, что G максимальная.
Victor Kleptsyn
М
19:46
Математические байки
Всё!
Victor Kleptsyn
М
19:48
Математические байки
Микеле, конечно, рассказывал не [только] об этом — это был лишь кусочек вводной части. А рассказывал он о том, как заставить группу Хигмана H_4 действовать на окружности —
Victor Kleptsyn
М
19:49
Математические байки
(Картинка отсюда — http://mtriestino.perso.math.cnrs.fr/Higman.pdf )
Victor Kleptsyn
М
20:11
Математические байки
Вообще, [сохраняющие ориентацию] действия групп на прямой (и на окружности) это очень красивая тема, соединяющая геометрию и алгебру. Например, оказывается, что действия на прямой связаны с лево-инвариантными порядками.
Victor Kleptsyn
М
20:11
Математические байки
А именно: назовём группу "левоупорядочиваемой" (left-orderable), если на ней есть полный порядок "<", инвариантный относительно умножения слева:
f<g <=> hf<hg
(такой порядок называется "левоинвариантным").
f<g <=> hf<hg
(такой порядок называется "левоинвариантным").
Victor Kleptsyn
М
20:12
Математические байки
Понятно, что для задания левоинвариантного порядка достаточно задать множество "положительных" (больших e) элементов группы. И легко перевести условия полного порядка на язык множества положительных элементов (произведение положительных положительно, любой элемент положительный, отрицательный или e).
Victor Kleptsyn
М
20:12
Математические байки
Но удивительным образом оказывается, что это связано с динамикой!
А именно — пусть группа G действует преобразованиями прямой, сохраняющими ориентацию. И пусть есть какая-нибудь точка x_0, которую ни один нетривиальный элемент G не оставляет на месте. Тогда это задаёт левоинвариантный порядок — будем говорить, что g<h, если g(x_0)<h(x_0)!
А именно — пусть группа G действует преобразованиями прямой, сохраняющими ориентацию. И пусть есть какая-нибудь точка x_0, которую ни один нетривиальный элемент G не оставляет на месте. Тогда это задаёт левоинвариантный порядок — будем говорить, что g<h, если g(x_0)<h(x_0)!
Victor Kleptsyn
М
20:28
Математические байки
Если есть несколько точек x_0,x_1,..., и ни одно преобразование не оставляет их все на месте одновременно — то можно устроить лексикографический левоинвариантный порядок:
g<h, если
* либо g(x_0)<h(x_0),
* либо g(x_0)=h(x_0), но g(x_1)<h(x_1),
* либо g(x_0)=h(x_0), g(x_1)=h(x_1), но g(x_2)<h(x_2),
и так далее.
g<h, если
* либо g(x_0)<h(x_0),
* либо g(x_0)=h(x_0), но g(x_1)<h(x_1),
* либо g(x_0)=h(x_0), g(x_1)=h(x_1), но g(x_2)<h(x_2),
и так далее.
Victor Kleptsyn
М
20:28
Математические байки
Наконец, взяв счётное всюду плотное множество точек на прямой (например, рациональные) — можно увидеть, что группа Homeo_+(R) вся левоупорядочиваема.
И, в частности, любая группа, которая умеет действовать на R сохраняющими ориентацию гомеоморфизмами так, чтобы никто не действовал тождественно — левоупорядочиваема.
И, в частности, любая группа, которая умеет действовать на R сохраняющими ориентацию гомеоморфизмами так, чтобы никто не действовал тождественно — левоупорядочиваема.
Victor Kleptsyn
М
20:30
Математические байки
На самом деле — если есть счётная группа G и левоинвариантный порядок на ней, то можно заставить её действовать на прямой так, чтобы порядок приходил из орбиты одной конкретной точки. (Это доказывается взятием начальной точку и последовательным построением её орбиты так, чтобы порядок точек был бы соответствующим порядку на группе.)
Так что если на счётной группе левый порядок есть, то он всегда приходит из [какого-то] действия!
Так что если на счётной группе левый порядок есть, то он всегда приходит из [какого-то] действия!
Victor Kleptsyn
М
20:30
Математические байки
Последнее замечание — одиночные соотношения из групп H_n,
aba^{-1}= b^2,
тоже связаны с действиями — это соотношение на преобразования a(x)=2x и b(x)=x+1.
aba^{-1}= b^2,
тоже связаны с действиями — это соотношение на преобразования a(x)=2x и b(x)=x+1.
Victor Kleptsyn
М
20:31
Математические байки
А вообще такие соотношения порождают группы Баумслага-Солитара, https://en.wikipedia.org/wiki/Baumslag–Solitar_group , из которых BS(1,n) это как раз группы, порождённые преобразованиями
x->nx и x->x+1,
и вообще хорошие и понятные — а вот общие BS(m,n) это (IMHO) ужас...
x->nx и x->x+1,
и вообще хорошие и понятные — а вот общие BS(m,n) это (IMHO) ужас...
Victor Kleptsyn
М
20:31
Математические байки
Ну и — про порядки на группах и их действия есть недавний текст (под кодовым названием GOD), "Groups, Order and Dynamics" —
https://arxiv.org/pdf/1408.5805.pdf
https://arxiv.org/pdf/1408.5805.pdf
Victor Kleptsyn
М
20:32
Математические байки
А я на сегодня прекращаю дозволенные речи (тем более, что получилось сложнее, чем обычно — но уж очень хотелось пересказать); а следующая байка будет с большим числом красивых картинок.
Victor Kleptsyn
27 November 2019
М
12:27
Математические байки
Вот такого замечательного доказательства формулы для синуса суммы углов я раньше не видел —
Victor Kleptsyn
М
12:27
Математические байки
Г
Геометрия-канал 22.11.2019 13:35:58
Наглядное доказательство формулы синуса суммы из книжки Ícons of Mathematics #картинка
Victor Kleptsyn
М
12:28
Математические байки
А ещё пользуюсь случаем порекламировать (если вдруг кто ещё не видел) —
Victor Kleptsyn
М
12:28
Математические байки
Н
М
12:28
Математические байки
Н
Непрерывное математическое образование 26.11.2019 22:00:43
в вышедшем сейчас втором издании мат. составляющей множество новых сюжетов (фактически это новая книга) и некоторые новые разделы
вот, например, «Книжная полка» — большой список книг по математике для самых разных читателей
вот, например, «Книжная полка» — большой список книг по математике для самых разных читателей
Victor Kleptsyn
М
12:28
Математические байки
===
Victor Kleptsyn
М
12:28
Математические байки
А сегодняшний рассказ будет про один из моих любимых сюжетов — про асимптотическую комбинаторику.
Victor Kleptsyn
М
12:30
Математические байки
Общая канва тут — берётся какой-нибудь комбинаторный объект, и задаются вопросы вроде "а сколько таких объектов заданного большого размера" или "на что похож такой типичный объект". Или — как устроены типичные отклонения от предельного поведения (но это уже следующий уровень сложности).
Victor Kleptsyn
М
12:33
Математические байки
Игрушечный пример — последовательности нулей и единиц. Их 2^n, а в типичной последовательности нулей и единиц примерно поровну. Наконец, отклонение от среднего числа имеет типичный порядок \sqrt{n}, и описывается центральной предельной теоремой — если на \sqrt{n} поделить, то частное ведёт себя (асимптотически) как случайная величина, распределённая по Гауссу.
Victor Kleptsyn
М
12:35
Математические байки
In reply to this message
(Собственно, мы даже это уже в этом канале обсуждали — см. сообщение выше)
Victor Kleptsyn
М
12:37
Математические байки
Чтобы получалась более комбинаторно-геометрическая картинка, можно превратить последовательность 0 и 1 в путь, идущий по квадратной решётке вправо при 0 и вверх при 1. Тогда при большом n путь, скорее всего, будет идти рядом с диагональю.
Victor Kleptsyn
М
12:38
Математические байки
Можно нарисовать картинки — только я разверну решётку на 45 градусов; путь тогда будет идти вправо-вверх и вправо-вниз, а в среднем просто вправо.
Victor Kleptsyn
М
12:38
Математические байки
Вот 30 шагов:
Victor Kleptsyn
М
12:39
Математические байки
Вот 100:
Victor Kleptsyn
М
12:39
Математические байки
Вот 300 (уже без решётки, иначе она превратится в сплошной чёрный фон):
Victor Kleptsyn
М
12:39
Математические байки
Ну и наконец, вот 3000 —
Victor Kleptsyn
М
12:40
Математические байки
А вот растянутая в корень из n раз по вертикали картинка — как раз отвечающая на вопрос про поведение типичных отклонений (n=1000):
Victor Kleptsyn
М
12:41
Математические байки
Это уже — (одномерное) броуновское движение (а точнее, его график как функции от времени).
Victor Kleptsyn
М
12:42
Математические байки
Пожалуй, самый сейчас известный пример из асимптотической комбинаторики — это ацтекский бриллиант.
Victor Kleptsyn
М
12:48
Математические байки
Вот тут есть рассказ о нём по-французски —
http://images.math.cnrs.fr/Pavages-aleatoires-par-touillage (но с языком можно справиться как Google Translate-ом, так и просто посмотреть на красивые картинки), ему посвящён вот этот математический постер — http://sorciersdesalem.math.cnrs.fr/Posters/PosterCercleArctique.png ; но я про него коротко расскажу с самого начала.
http://images.math.cnrs.fr/Pavages-aleatoires-par-touillage (но с языком можно справиться как Google Translate-ом, так и просто посмотреть на красивые картинки), ему посвящён вот этот математический постер — http://sorciersdesalem.math.cnrs.fr/Posters/PosterCercleArctique.png ; но я про него коротко расскажу с самого начала.
Victor Kleptsyn
М
12:51
Математические байки
А по-русски про него можно подробно прочитать в дубнинской брошюре Е. Смирнова, "Три взгляда на ацтекский бриллиант",
https://www.mccme.ru/free-books/dubna/smirnov-aztec.pdf
https://www.mccme.ru/free-books/dubna/smirnov-aztec.pdf
Victor Kleptsyn
М
12:52
Математические байки
Так вот, если формально, то ацтекский бриллиант (aztec diamond) это фигура, составленная из квадратиков на квадратной решётке, у которых сумма модулей абсциссы и ординаты центра не превосходит заданной величины (которая называется порядком бриллианта).
В переводе на русский — он выглядит вот так:
В переводе на русский — он выглядит вот так:
Victor Kleptsyn
М
12:53
Математические байки
Собственно, вот отсюда происходит название: ацтекский, потому что как пирамиды ацтеков, и diamond, потому что это слово употребляется в значении "ромб" (ну, точнее, тоже квадрат, но повёрнутый на 45 градусов)
Victor Kleptsyn
М
12:54
Математические байки
Так вот, комбинаторный объект, с которым мы тут работаем, это разбиения этого бриллианта на доминошки — на прямоугольники 1x2.
Victor Kleptsyn
М
12:54
Математические байки
Кстати, цитируя коллег —
Victor Kleptsyn
М
12:55
Математические байки
q
qtasep 15.10.2019 18:23:46
Не знаю, когда там ребенка пора начинать учить математике, но современную теорию вероятностей я уже ему показываю (см. например тут https://en.wikipedia.org/wiki/Aztec_diamond - а 3D картинки можно увидеть, например, тут: http://math.mit.edu/~borodin/aztec.html). На русском языке есть обзор Е. Смирнова https://www.mccme.ru/free-books/dubna/smirnov-aztec.pdf
Victor Kleptsyn
М
12:57
Математические байки
Вообще-то, наши вопросы уже можно задавать:
- сколько у АБ порядка n разбиений на доминошки?
- на что похоже типичное разбиение?
Но ответ на второй вопрос в таком виде получится не очень наглядным, поэтому давайте сначала добавим к этой картинке цвет.
- сколько у АБ порядка n разбиений на доминошки?
- на что похоже типичное разбиение?
Но ответ на второй вопрос в таком виде получится не очень наглядным, поэтому давайте сначала добавим к этой картинке цвет.
Victor Kleptsyn
М
12:58
Математические байки
А именно — сначала (как на кружке) наложим на АБ шахматную раскраску:
Victor Kleptsyn
М
12:59
Математические байки
Тогда каждая доминошка закрывает одну чёрную и одну белую клетку.
Victor Kleptsyn
М
13:03
Математические байки
Давайте договоримся, что если доминошка от чёрной клетки идёт
- вверх, то мы её красим в жёлтый цвет,
- вниз, то мы её красим в красный цвет,
- вправо, то мы её красим в зелёный цвет,
- влево, то мы её красим в синий цвет:
- вверх, то мы её красим в жёлтый цвет,
- вниз, то мы её красим в красный цвет,
- вправо, то мы её красим в зелёный цвет,
- влево, то мы её красим в синий цвет:
Victor Kleptsyn
М
М
13:04
Математические байки
(В частности, горизонтальные доминошки так оказываются покрашены в "холодные" цвета, а вертикальные в "тёплые")
Victor Kleptsyn
М
13:05
Математические байки
Так вот — давайте посмотрим на то, как выглядит одно разбиение АБ порядка n на доминошки, случайно выбранное из всех возможных вариантов (я, правда, до сих пор не сказал, сколько их).
Victor Kleptsyn
М
13:05
Математические байки
Сначала — n=10:
Victor Kleptsyn
М
13:06
Математические байки
И вторая попытка с n=10:
Victor Kleptsyn
М
13:06
Математические байки
Теперь n=50:
Victor Kleptsyn
М
13:06
Математические байки
И наконец, n=200:
Victor Kleptsyn
М
13:11
Математические байки
И вот он, красивый эффект — "теорема о полярном круге": снаружи от вписанной окружности все доминошки оказываются "заморожены".
Её доказали Jockush, Propp и Shor; см. — https://arxiv.org/abs/math/9801068
Её доказали Jockush, Propp и Shor; см. — https://arxiv.org/abs/math/9801068
Victor Kleptsyn
М
13:13
Математические байки
Кстати, у них в работе есть и картинка без раскраски:
Victor Kleptsyn
М
13:14
Математические байки
Видно, что без цвета всё гораздо менее наглядно...
Victor Kleptsyn
М
13:16
Математические байки
Возвращаясь к ацтекскому бриллианту — одну красивую картинку мы увидели, но вот что за нею стоит?
Оказывается, что стоит довольно много.
Оказывается, что стоит довольно много.
Victor Kleptsyn
М
13:17
Математические байки
Начать с того, что я продекларировал, что разбиение выбрано равновероятно из всех возможностей — но совершенно не сказал, как это сделано. И даже не сказал, сколько их вообще.
Victor Kleptsyn
М
13:23
Математические байки
К равновероятному выбору мы ещё вернёмся — а пока посмотрим, сколько их должно быть.
Victor Kleptsyn
М
13:27
Математические байки
Во-первых, сделаем оценку сверху: площадь АБ порядка n равна 2n(n+1); половина её это чёрные клетки, так что их n(n+1). Собственно, если нарисовать первые сколько-то АБ, то это видно "на глаз":
Victor Kleptsyn
М
13:29
Математические байки
(picture credit: картинка из статьи в Images de Maths, которую я упоминал выше)
Так вот — разбиение кодируется набором направлений доминошек, закрывающих эти клетки. Значит, всего разбиений не больше, чем
4^{n(n+1)}.
Так вот — разбиение кодируется набором направлений доминошек, закрывающих эти клетки. Значит, всего разбиений не больше, чем
4^{n(n+1)}.
Victor Kleptsyn
М
13:33
Математические байки
Во-вторых, сделаем теперь оценку снизу. В ацтекский бриллиант порядка n=2m-1 (и n=2m) можно вписать честный квадрат размера 2mx2m, "срезав уголки".
Уголки можно разрезать на доминошки просто параллельно линии отреза — а квадрат размера 2mx2m разрезать на m^2 квадратов размера 2x2.
Уголки можно разрезать на доминошки просто параллельно линии отреза — а квадрат размера 2mx2m разрезать на m^2 квадратов размера 2x2.
Victor Kleptsyn
М
13:34
Математические байки
Каждый из этих квадратов разрезается на доминошки двумя способами — и вот мы получили оценку снизу как 2^{m^2}, то есть примерно как 2^{n^2/4}.
Victor Kleptsyn
М
13:35
Математические байки
И оценка сверху, и оценка снизу экспоненциальные по площади АБ. То есть естественно ожидать, что асимптотика будет exp(c n^2), где c — некоторая, пока неизвестная нам, константа.
Victor Kleptsyn
М
13:37
Математические байки
Вообще — такие ситуации, когда число вариантов экспоненциально по числу задействованных объектов (квадратиков или доминошек, в данном случае), встречаются исключительно часто. А множитель в экспоненте обычно тогда называют энтропией.
Victor Kleptsyn
М
13:39
Математические байки
Игрушечный пример — тоже разбиения на доминошки, но прямоугольника 2xn. Упражнение: их количество это (n+1)-е число Фибоначчи.
Учитывая то, как растут числа Фибоначчи — энтропией будет логарифм золотого сечения.
Учитывая то, как растут числа Фибоначчи — энтропией будет логарифм золотого сечения.
Victor Kleptsyn
М
13:41
Математические байки
Но аналогия тут идёт сильно дальше — и соседняя огромная область это статистическая физика. Где будут, например, возможные конфигурации атомов — в количестве, экспоненциальном по числу задействованных атомов.
Victor Kleptsyn
М
13:43
Математические байки
In reply to this message
Кстати, в качестве рекламы — (IMHO, очень хороший) текст Окунькова как раз о статистической физике: http://book.etudes.ru/toc/patternhappen/
Victor Kleptsyn
М
13:47
Математические байки
Но давайте вернёмся к собственно подсчёту разбиений. Ответ про их количество оказывается тоже удивительным (и вдвойне — что получается посчитать их точно, а не только найти асимптотику).
Victor Kleptsyn
М
13:48
Математические байки
Теорема (N. Elkies, G. Kuperberg, M. Larsen, J. Propp): Количество разбиений АБ порядка n равно 2^{n(n+1)/2}.
См.: https://arxiv.org/abs/math/9201305
См.: https://arxiv.org/abs/math/9201305
Victor Kleptsyn
М
13:55
Математические байки
Собственно, трём взглядам на разбиения АБ и трём доказательствам этой теоремы и посвящена брошюра Е. Смирнова, что я упоминал — так что тут я дальше не пойду. Правда, покажу (без объяснения) одну из картинок — про модель "квадратного льда", с которой ацтекский бриллиант оказывается связанным:
Victor Kleptsyn
М
13:56
Математические байки
Зато — нам этого ответа уже хватит, чтобы понять, что _угловые_ доминошки действительно должны быть ориентированы так, как предсказывает теорема о полярном круге:
Victor Kleptsyn
М
13:57
Математические байки
Действительно, пусть мы закрыли угловую клетку горизонтальной доминошкой:
Victor Kleptsyn
М
13:58
Математические байки
Тогда у клетки B остался только один сосед — так что и её придётся закрывать горизонтальной доминошкой:
Victor Kleptsyn
М
13:58
Математические байки
А тогда и клетку C, и так далее: пошла "лесенка":
Victor Kleptsyn
М
13:59
Математические байки
Более того, такая же лесенка пойдёт и вниз:
Victor Kleptsyn
М
М
14:01
Математические байки
(потому что разница двух треугольных чисел в показателе как раз равна n).
Victor Kleptsyn
М
14:02
Математические байки
Понятно, что начиная с n=10, мы событий столь малой вероятности практически не увидим.
Victor Kleptsyn
М
14:06
Математические байки
Ну и это подсказывает общую точку зрения: мы видим такую картинку, как выше, не потому, что что-либо иное совсем запрещено — а потому, что их просто сильно меньше, чем всех.
Точно так же, как выкинуть 10 орлов из 100 подбрасываний не запрещено — но число способов это сделать сильно-сильно меньше, чем общее число вариантов.
Точно так же, как выкинуть 10 орлов из 100 подбрасываний не запрещено — но число способов это сделать сильно-сильно меньше, чем общее число вариантов.
Victor Kleptsyn
М
14:09
Математические байки
И кстати, это же подсказывает, что "наивные" методы построения случайного разбиения не пройдут: нельзя, например, взять какую-нибудь свободную клетку, подкинуть монетку, чтобы решить, куда пойдёт из неё доминошка, и перейти к следующей свободной клетке. Потому что при _равномерном_ выборе разбиения шанс, что доминошка в левом углу вертикальная, должен быть близок к 1. А вовсе не, скажем, 1/2.
Victor Kleptsyn
М
14:13
Математические байки
Более того, это же подсказывает, что нет у нас шансов и выбрать случайное разбиение, сначала перечислив их все: уже для n=10, их количество это
2^{n(n+1)/2} = 2^55, и получается совсем не тот объём информации, который можно хранить на компьютере (учитывая, что каждый ещё и задавать надо, и это не один бит — получается порядок эксабайт(!))...
2^{n(n+1)/2} = 2^55, и получается совсем не тот объём информации, который можно хранить на компьютере (учитывая, что каждый ещё и задавать надо, и это не один бит — получается порядок эксабайт(!))...
Victor Kleptsyn
М
14:14
Математические байки
Нет, конечно, я не то, чтобы вру, но сгущаю краски — можно и считать, и генерировать "бегущим профилем", и это сразу нас вернёт в разумные количества. Но до n=200 даже так, "грубой силой", не дотянуться.
Victor Kleptsyn
М
14:30
Математические байки
Так как же можно нарисовать случайное разбиение?
(А картинки выше действительно были выбраны равновероятно среди всех — ну, точнее, равновероятно в пределах точности компьютерного датчика случайных чисел.)
Оказывается, для АБ есть сразу несколько способов это сделать — но прежде, чем их описывать, мне хочется дополнительно мотивировать разбиения на доминошки как объекта изучения.
Тут, на самом деле, можно много чего сказать (примерно на годовой спецкурс — легко), но простейшая мотивация — это переход с квадратной решётки на треугольную.
(А картинки выше действительно были выбраны равновероятно среди всех — ну, точнее, равновероятно в пределах точности компьютерного датчика случайных чисел.)
Оказывается, для АБ есть сразу несколько способов это сделать — но прежде, чем их описывать, мне хочется дополнительно мотивировать разбиения на доминошки как объекта изучения.
Тут, на самом деле, можно много чего сказать (примерно на годовой спецкурс — легко), но простейшая мотивация — это переход с квадратной решётки на треугольную.
Victor Kleptsyn
М
14:33
Математические байки
Пусть мы разбиваем область на треугольной решётке — скажем, просто большой правильный шестиугольник — на "доминошки"-ромбики из двух соседних треугольников:
Victor Kleptsyn
М
14:34
Математические байки
Достаточно раскрасить ромбики в разбиении (а они тут будут трёх возможных направлений, так что красим в три цвета) —
Victor Kleptsyn
М
14:35
Математические байки
— и картинка становится "кубиками" в трёхмерном пространстве (собранными в углу комнаты).
Victor Kleptsyn
М
14:45
Математические байки
Тут уже можно и сделать аллюзию на диаграммы Юнга (такие же кубики в углу, но двумерной комнаты, они же число способов разбить число n в сумму натуральных слагаемых без учёта порядка) — и вспомнить формулу МакМагона для подсчёта числа таких "заполнений кубиками" в комнате размера axbxc (мне, опять-таки, вспоминается — другая — брошюра Е. Смирнова, https://www.mccme.ru/free-books/dubna/smirnov-asm.pdf , см. лекцию 3 ) — ну, в общем, я же уже говорил про годовой курс?
Victor Kleptsyn
М
14:45
Математические байки
Но мне из этой картинки хочется вытащить "функцию высоты" и вообще трёхмерный взгляд на неё.
Victor Kleptsyn
М
14:48
Математические байки
Оказывается, этот взгляд нам (сразу несколькими способами) может помочь сгенерировать случайное разбиение.
Victor Kleptsyn
М
14:49
Математические байки
Пусть у нас есть разбиение на ромбики на треугольной решётке. Если в нём есть шестиугольник со стороной 1, разбитый на три ромбика одним способом — можно его переразбить другим. Назовём это "элементарной перестройкой".
Victor Kleptsyn
М
14:50
Математические байки
Теорема. Пусть на треугольной решётке задана область "без дырок" (например, наш большой правильный шестиугольник). Тогда от любого её разбиения на ромбики до любого другого можно дойти чередой элементарных перестроек.
Victor Kleptsyn
М
14:53
Математические байки
"Доказательство". Трёхмерный взгляд позволяет посмотреть на картинку, как просто на добавление/убирание кубика. Будем убирать кубики "от самого верхнего", пока не дойдём от любого исходного разбиения до состояния "пустая комната".
Victor Kleptsyn
М
14:55
Математические байки
От любого состояния дошли до одного и того же, минимального — значит, от любого можно дойти до любого другого.
(Я взял слово "доказательство" в кавычки — потому что это для настоящей комнаты легко сказать, что означает "пустая комната", а так нужно действовать чуть более аккуратно. Но давайте считать, что тут я всё заметаю под ковёр.)
(Я взял слово "доказательство" в кавычки — потому что это для настоящей комнаты легко сказать, что означает "пустая комната", а так нужно действовать чуть более аккуратно. Но давайте считать, что тут я всё заметаю под ковёр.)
Victor Kleptsyn
М
14:57
Математические байки
То же самое можно сделать и для разбиений (опять таки, областей без дырок) на квадратной решётке — а в качестве элементарной перестройки выступает переразбиение квадрата 2x2.
Victor Kleptsyn
М
15:01
Математические байки
Так вот, возвращаясь к ацтекскому бриллианту. Вообще, картинки, которые я показывал, нарисованы с использованием специфики именно ацтекского бриллианта. А именно, одно из доказательств теоремы о числе разбиений позволяет ещё и по честно-равномерному разбиению АБ порядка (n-1), дополнительно несколько раз подбросив монетку, получить честно-равномерное разбиение АБ порядка n. И завязано это как раз на функцию высоты (которая достраивает картинку до трёхмерной) — рассматриваемую в одном случае в чёрных, а в другом в белых вершинах. Но в эту технику я не пойду, именно потому, что она завязана на конкретику АБ.
Victor Kleptsyn
М
15:02
Математические байки
Но можно себе представить другой способ порождать случайные разбиения — с помощью случайного блуждания.
Victor Kleptsyn
М
15:03
Математические байки
А именно: рассмотрим граф, вершинами которого являются _все_ разбиения АБ, а рёбра соединяют разбиения, отличающиеся на элементарную перестройку.
Victor Kleptsyn
М
15:04
Математические байки
Этот граф, конечно, объект чисто абстрактный: для порядка n=100 у него 2^{5050} вершин, что немного многовато.
Victor Kleptsyn
М
15:05
Математические байки
Зато рёбер из каждой вершины выходит не так много — не больше 2n^2=20.000, что вполне компьютерно-реалистично.
Victor Kleptsyn
М
15:05
Математические байки
И можно рассмотреть блуждание по такому графу — приходим в вершину, уходим по случайно выбранному ребру, оттуда опять по случайно выбранному ребру, и так далее.
Victor Kleptsyn
М
15:09
Математические байки
Так вот — если так "побродить" достаточно долго, то получается (почти) равновероятное распределение на том, куда мы в принципе можем прийти. И это и есть один из способов генерации случайного разбиения. Но тут нужно быть аккуратным и в том, как генерировать, и в том, когда останавливаться (а ещё есть красивые слова "coupling from the past", которые позволяют гарантировать, что получаемое разбиение совсем честно случайно).
Victor Kleptsyn
М
15:09
Математические байки
И это, кажется, хороший момент, чтобы сделать паузу в рассказе...
Victor Kleptsyn
2 December 2019
М
13:20
Математические байки
In reply to this message
Добрался до Лиона, и теперь могу показать кусочки их математической фрески в лучшем качестве:
Victor Kleptsyn
М
13:20
Математические байки
Воздушный шар с расслоением Хопфа —
Victor Kleptsyn
М
13:21
Математические байки
Солнце, универсально накрывающее сферу без трёх точек —
Victor Kleptsyn
М
13:21
Математические байки
Дикий узел —
Victor Kleptsyn
М
13:31
Математические байки
In reply to this message
Кстати — вот одно из совершенно потрясающих рассуждений в комплексном анализе (увы — для тех, кто его уже немного знает), теорема Пикара. Целая (голоморфная на C) функция, не принимающая хотя бы два значения, константа.
Потому что — универсальная накрывающая над C без двух точек это диск. Непрерывное отображение можно поднять до отображения универсальных накрывающих. А универсальная накрывающая над C без двух точек (=над сферой без трёх) это диск.
И если мы начали с целой функции, бьющей в C без двух точек — то получаем отображение из C в диск, то есть ограниченную целую функцию. А ограниченная целая функция — константа.
Потому что — универсальная накрывающая над C без двух точек это диск. Непрерывное отображение можно поднять до отображения универсальных накрывающих. А универсальная накрывающая над C без двух точек (=над сферой без трёх) это диск.
И если мы начали с целой функции, бьющей в C без двух точек — то получаем отображение из C в диск, то есть ограниченную целую функцию. А ограниченная целая функция — константа.
Victor Kleptsyn
3 December 2019
М
12:51
Математические байки
Часы в чайной комнате UMPA тоже соответствующие —
Victor Kleptsyn
М
12:53
Математические байки
In reply to this message
Но давайте я продолжу этот рассказ. Итак, пусть у нас есть абы какой связный граф G. Рассмотрим вот такой процесс на нём: мы начинаем из какой-то вершины, и каждый раз переходим в случайно выбранного соседа этой вершины.
Victor Kleptsyn
М
13:00
Математические байки
Вообще, такие процессы называются _цепями Маркова_. "Такие" — это значит, что есть множество состояний, для каждого состояния задано, с какой вероятностью в какое состояние мы переходим, причём эта вероятность зависит только от того, где мы сейчас, но не от того, где мы были раньше. Ну и — чтобы процесс был задан полностью, нужно ещё задать начальное распределение (где и с какой вероятностью мы начинаем; например, можно начать просто в заданной точке).
Victor Kleptsyn
М
13:01
Математические байки
"Игрушечный пример" тут — лягушки, прыгающие между сушей и болотом. Допустим, что лягушка на суше понимает, что ей там плохо, и всегда прыгает в болото. А лягушкам в болоте интересно, что там на суше, и каждая из них решает, остаться там или рискнуть выползти на сушу, с вероятностью 1/2.
Посмотрим, как будет делиться популяция лягушек, если в начальный момент они все сидят в болоте:
Посмотрим, как будет делиться популяция лягушек, если в начальный момент они все сидят в болоте:
Victor Kleptsyn
М
13:10
Математические байки
Невооружённым глазом видно, что распределение лягушек сошлось к соотношению "2/3 в болоте, 1/3 на суше", которое за один шаг переходит в себя. Такое распределение называется _стационарным_.
Оно всегда (ну, пока граф конечный) есть: средние арифметические распределений за первые n шагов всё более и более стационарны, и достаточно взять их предельную точку. И при довольно простых условиях оно единственно и к нему будет сходимость (как мы и видели на примере лягушек выше). А именно, достаточно попросить, чтобы:
- от любого состояния можно было допрыгать до любого (ибо если есть две не связанных экосистемы, то можно комбинировать меру на одной с мерой на другой)
- НОД возможных времён допрыгивания от состояния до себя равнялся бы 1 (если граф состояний двудольный, то лягушки, начавшие в чёрных вершинах, каждый чётный ход и будут в чётных вершинах — и никакого уравновешения).
Оно всегда (ну, пока граф конечный) есть: средние арифметические распределений за первые n шагов всё более и более стационарны, и достаточно взять их предельную точку. И при довольно простых условиях оно единственно и к нему будет сходимость (как мы и видели на примере лягушек выше). А именно, достаточно попросить, чтобы:
- от любого состояния можно было допрыгать до любого (ибо если есть две не связанных экосистемы, то можно комбинировать меру на одной с мерой на другой)
- НОД возможных времён допрыгивания от состояния до себя равнялся бы 1 (если граф состояний двудольный, то лягушки, начавшие в чёрных вершинах, каждый чётный ход и будут в чётных вершинах — и никакого уравновешения).
Victor Kleptsyn
М
13:22
Математические байки
Слово "стационарный" здесь можно читать просто как аналог слова "инвариантный"/"сохраняющийся операцией", но правильнее так: если взять эту меру в качестве уже начального распределения, то процесс получается инвариантен относительно сдвига по времени. И тут могло бы быть ответвление в сторону космологии, Фридмана, стационарных/нестационарных моделей Вселенной и нетривиальности понимания того, что Вселенная может быть нестационарной, но я, боюсь, всё-таки не готов его писать менее пунктирно и при этом не рисковать соврать более допустимого. :)
Victor Kleptsyn
М
13:22
Математические байки
Так вот, к чему всё это — к тому, что у нашего "случайного блуждания по графу" тоже есть стационарная мера. Причём мера очень простая и понятная: вероятность вершины пропорциональна степени этой вершины.
Victor Kleptsyn
М
13:24
Математические байки
Действительно: если вероятность каждой вершины v равна d(v)/Z, где Z — сумма степеней всех вершин (то есть удвоенное число рёбер, что, впрочем, неважно), то для каждого ребра за один шаг по нему в каждую из сторон прыгает одна и та же масса "лягушек" — а именно, 1/Z. Значит, в каждой вершине сколько было, столько и осталось.
Victor Kleptsyn
М
13:30
Математические байки
И кусочки головоломки "выбрать случайную вершину" уже почти склеились: мы знаем, что при простых условиях, даже если мы начинаем в детерминированной вершине, распределение вероятностей сходится к стационарной мере, и стационарная мера блуждания уже очень похожа на равномерную (но ещё не!).
Victor Kleptsyn
М
13:32
Математические байки
Но условия проверять нужно — а именно, нужно бороться с двудольностью графа (а то при хождении по кубу, если мы начали в чёрной вершине, то мы каждый чётный ход сможем быть только в чёрной вершине, а не в любой вообще).
Victor Kleptsyn
М
13:37
Математические байки
Починим сразу и то, и другое — добавлением фальшивых рёбер. Пусть мы знаем, что у нас всегда меньше D рёбер. Тогда можно сделать так: кинуть кубик с D гранями — если выпало число от 1 до d, где d степень текущей вершины, то перейти по соответствующему ребру, а если больше, то остаться на месте.
Victor Kleptsyn
М
13:47
Математические байки
Опять-таки, игрушечный пример — 100-мерный куб {0,1}^100. Его вершины — все возможные 2^100 последовательностей 0 и 1, и это совершенно "наш" случай, что все перечислить нельзя.
Конечно, можно просто подкинуть монетку 100 раз (и это как раз пример, аналогичный ацтекскому бриллианту — когда именно для данного графа, из-за его специфики, есть быстрый способ выбрать случайную вершину) — но допустим, что мы это сделать не догадались.
Конечно, можно просто подкинуть монетку 100 раз (и это как раз пример, аналогичный ацтекскому бриллианту — когда именно для данного графа, из-за его специфики, есть быстрый способ выбрать случайную вершину) — но допустим, что мы это сделать не догадались.
Victor Kleptsyn
М
13:51
Математические байки
Начав в конкретной точке (например, (0,...,0)) — мы на каждом шагу с вероятностью 1/101 переходим по каждому из возможных рёбер, а ещё с вероятностью 1/101 остаёмся на месте. Иными словами, мы либо меняем один из разрядов нашего 100-значного двоичного слова, либо (с небольшой вероятностью) не делаем ничего.
После того, как мы сделаем такое где-нибудь 10000 раз, каждый разряд мы поменяли в среднем около сотни раз. И "ежу понятно" (хотя, конечно, надо доказывать!), что на такой куче "перещёлкиваний" мы получили уже почти-совсем-случайное распределение.
После того, как мы сделаем такое где-нибудь 10000 раз, каждый разряд мы поменяли в среднем около сотни раз. И "ежу понятно" (хотя, конечно, надо доказывать!), что на такой куче "перещёлкиваний" мы получили уже почти-совсем-случайное распределение.
Victor Kleptsyn
М
16:58
Математические байки
Казалось бы, отсюда можно получить уже готовый рецепт генерации (почти) случайного разбиения ацтекского бриллианта. А именно: мы знаем, что граф с вершинами-разбиениями связен относительно перестроек квадратиков. Берём какое-нибудь фиксированное начальное разбиение, например, просто все доминошки ставим вертикально. И на каждом шаге выбираем случайный квадрат 2x2. Если его можно перестроить — перестраиваем. Если нельзя — не трогаем. Как раз получается добавление фальшивых рёбер (ибо теперь у нас из каждой вершины исходит одно и то же их количество — просто многие ведут в неё же).
Victor Kleptsyn
М
16:59
Математические байки
Вот пример такой симуляции (за эти картинки спасибо И. Батманову и К. Люборту):
Victor Kleptsyn
М
17:00
Математические байки
первая перестройка —
Victor Kleptsyn
М
17:00
Математические байки
вторая —
Victor Kleptsyn
М
17:01
Математические байки
третья —
Victor Kleptsyn
М
17:01
Математические байки
20-я —
Victor Kleptsyn
М
17:02
Математические байки
(кстати, видно, что один из квадратиков "развернулся обратно")
Victor Kleptsyn
М
17:02
Математические байки
40-я — пары горизонтальных доминошек посередине уже порождают вертикальные другой чётности
Victor Kleptsyn
М
17:03
Математические байки
это уже 100-я — волна перестроек "расползается"
Victor Kleptsyn
М
17:03
Математические байки
Это была 500-я
Victor Kleptsyn
М
17:03
Математические байки
1500-я:
Victor Kleptsyn
М
17:03
Математические байки
3000-я:
Victor Kleptsyn
М
17:03
Математические байки
6000-я:
Victor Kleptsyn
М
17:04
Математические байки
И при взгляде на всё это должен появиться вопрос — а когда пора остановиться? _Сколько именно_ нужно ждать, чтобы можно было сказать, что да, мы получили что-то "почти случайное"?
Victor Kleptsyn
М
17:11
Математические байки
Вопрос из этой же серии — а сколько раз нужно перетасовывать колоду, чтобы порядок карт в ней можно было считать случайным? Народ вполне серьёзно этим вопросом занимался — и я тут ограничусь ссылкой на текст Американского Математического Общества:
http://www.ams.org/publicoutreach/feature-column/fcarc-shuffle
http://www.ams.org/publicoutreach/feature-column/fcarc-shuffle
Victor Kleptsyn
М
17:15
Математические байки
То, что он может быть сильно нетривиальным, можно увидеть на примере того же многомерного куба. Скажем, понятно, что бессмысленно делать число итераций меньшее, чем диаметр графа — мы тогда просто не сумеем от любой вершины дойти до любой. Но оказывается, что иногда характерное "время перемешивания" (собственно, оно так и называется, "mixing time") — гораздо больше.
Victor Kleptsyn
М
17:16
Математические байки
Давайте возьмём два куба, один 100-мерный, другой 200-мерный. И соединим в них лишь одну вершину одного с одной вершиной другого. (Например, "все единицы" со "всеми единицами".)
Victor Kleptsyn
М
17:23
Математические байки
Тогда случайное блуждание, начавшееся в 100-мерном кубе (например, в точке "все нули"), будет там блуждать как минимум до первого попадания в точку перехода в 200-мерный куб. Соответственно, на временах, заметно меньших 2^100 итераций, мы будем видеть только пренебрежимо малую (2^100 по сравнению с 2^200) долю вершин нашего графа.
(А если 100 в этом примере мало — возьмём 1000, и можно будет написать "за всё время существования Вселенной".)
Ну и, собственно, проблема явно видна — "перешейки". Вопрос только в том, что с ними делать.
(А если 100 в этом примере мало — возьмём 1000, и можно будет написать "за всё время существования Вселенной".)
Ну и, собственно, проблема явно видна — "перешейки". Вопрос только в том, что с ними делать.
Victor Kleptsyn
М
17:33
Математические байки
И ещё два слова я ещё скажу, а пока, в качестве иллюстрации сложности — большая книга, которая так и называется: "Markov chains and mixing times" — https://pages.uoregon.edu/dlevin/MARKOV/markovmixing.pdf
Victor Kleptsyn
М
17:42
Математические байки
In reply to this message
Кстати — левая иллюстрация на обложке как раз на нашу тему, только я показать её забыл: это случайное разбиение, но на шестиугольной, а не на квадратной, решётке. Раскрашенное в три цвета — то есть выглядящее, как кубики, сложенные в углу комнаты.
И я забыл сказать, что для этого случая тоже есть "теорема о полярном круге" —
И я забыл сказать, что для этого случая тоже есть "теорема о полярном круге" —
Victor Kleptsyn
М
17:43
Математические байки
(Каюсь, не помню, чья это иллюстрация — но не моя. У Кеньона есть похожая, но чуть-чуть в других цветах — http://www.math.brown.edu/~rkenyon/gallery/bppsim.gif )
Victor Kleptsyn
М
17:50
Математические байки
Кстати: можно пытаться брать не равновероятное — а как-то взвешенное распределение. Например, раз уж мы всё равно смотрим на эту картинку как на кубики — зафиксировать объём. Или (что приводит к очень близкому результату) — сказать, что пусть вероятность разбиения (то есть пирамидки из кубиков) пропорциональна параметру q в степени количество кубиков. (И тут опять начинается статистическая физика, exp(-\beta H) и всё такое). И получим мы, вместо теоремы о полярном круге — предельную форму угла кубического монокристалла:
Victor Kleptsyn
М
17:51
Математические байки
(Picture credit : A. Okounkov)
Victor Kleptsyn
М
17:59
Математические байки
Обещанные несколько слов:
— Во-первых, у нас тут выше вырисовалась связка (всё связано со всем) "случайное блуждание—время перемешивания—спектр оператора Лапласа—изопериметрическое неравенство".
Ну, почти вырисовалась — ещё нужно сказать, что за случайное блуждание как раз оператор Лапласа и отвечает, а за "бутылочные горлышки" отвечает изопериметрическое неравенство.
— Во-первых, у нас тут выше вырисовалась связка (всё связано со всем) "случайное блуждание—время перемешивания—спектр оператора Лапласа—изопериметрическое неравенство".
Ну, почти вырисовалась — ещё нужно сказать, что за случайное блуждание как раз оператор Лапласа и отвечает, а за "бутылочные горлышки" отвечает изопериметрическое неравенство.
Victor Kleptsyn
11 December 2019
М
20:26
Математические байки
In reply to this message
(Прошу прощения — такой большой перерыв не планировался...)
Так вот, во-вторых, тут неподалёку живут слова "концентрация меры".
Так вот, во-вторых, тут неподалёку живут слова "концентрация меры".
Victor Kleptsyn
М
20:27
Математические байки
А именно: как совсем широко известно, стомерные арбузы покупать не стоит. Ибо состоят они в основном из кожуры: даже если толщина кожуры это 5% — доля съедобной части в арбузе будет 0.95^100 ~ e^{-5} ~ 0.0067.
Victor Kleptsyn
М
20:27
Математические байки
А вот как чуть менее широко известно, многомерный арбуз состоит в основном из своего экватора. Из какого? Да из любого!
Victor Kleptsyn
М
20:28
Математические байки
А именно — возьмём случайно выбранную точку (x_1,...,x_n) на n-1-мерной единичной сфере.
Посмотрим на первую координату, x_1.
Её модуль — это и есть расстояние до экваториальной сферы, {x_1=0}.
Посмотрим на первую координату, x_1.
Её модуль — это и есть расстояние до экваториальной сферы, {x_1=0}.
Victor Kleptsyn
М
20:29
Математические байки
Но поскольку сумма квадратов всех n координат равна единице,
x_1^2+...+x_n^2=1,
то "естественно ожидать", что на квадрат каждой координаты в среднем приходится по 1/n. То есть x_1 (который вообще-то принимает значения от -1 до 1) "обычно" будет иметь порядок 1/sqrt{n}.
x_1^2+...+x_n^2=1,
то "естественно ожидать", что на квадрат каждой координаты в среднем приходится по 1/n. То есть x_1 (который вообще-то принимает значения от -1 до 1) "обычно" будет иметь порядок 1/sqrt{n}.
Victor Kleptsyn
М
20:29
Математические байки
И это таки да правда — и более того, при увеличении n распределение произведения \sqrt{n}*x_1 сходится к гауссову нормальному распределению N(0,1) — тому самому, которое самое замечательное в теории вероятностей, и сходимость к которому утверждает ЦПТ.
Victor Kleptsyn
М
20:38
Математические байки
Наиболее простой способ это увидеть такой. Давайте возьмём n независимых, распределённых как N(0,1) случайных величин \xi_k. Тогда у каждой из них плотность это (1/sqrt{2π}) * exp(-x^2/2), а совместная плотность в R^n — это их произведение, то есть
1/(2π)^{n/2} * exp(-r^2/2), где r^2=x_1^2+...+x_n^2 — радиус.
1/(2π)^{n/2} * exp(-r^2/2), где r^2=x_1^2+...+x_n^2 — радиус.
Victor Kleptsyn
М
20:39
Математические байки
Тогда это распределение сферически симметричное: плотность в R^n у него зависит только от расстояния до начала координат. Значит, если мы спроецируем выбранную таким образом точку на единичную сферу — получится равномерно распределённая точка на сфере. И её первая координата будет равна
x_1=\xi_1/r.
x_1=\xi_1/r.
Victor Kleptsyn
М
20:39
Математические байки
Но r^2=x_1^2+...+x_n^2 — это сумма n _независимых_ одинаково распределённых случайных величин. И как нас учит закон больших чисел, r^2/n с очень большой вероятностью близко к математическому ожиданию любой из них — то есть к единице.
Victor Kleptsyn
М
20:40
Математические байки
То есть r это "почти константа \sqrt{n}". Ну а исходная случайная величина \xi_1 была точно N(0,1).
Значит,
\sqrt{n}* x_1 = \xi_1 * (\sqrt{n}/r) —
почти N(0,1), и чем больше n, тем точнее это "почти".
Значит,
\sqrt{n}* x_1 = \xi_1 * (\sqrt{n}/r) —
почти N(0,1), и чем больше n, тем точнее это "почти".
Victor Kleptsyn
М
20:41
Математические байки
Вернёмся теперь к словам "концентрация меры". А именно — пусть на n-мерной единичной сфере задана какая-то 1-липшицева функция f (то есть такая, что |f(x)-f(y)|<|x-y|) — как в примере выше мы рассматривали функцию f(x_1,...,x_n)=x_1.
Victor Kleptsyn
М
20:42
Математические байки
Посмотрим на распределение её значений — на какой доле площади точек сферы она принимает какие значения. Оказывается (и это и есть эффект "концентрации меры"), что в основном эти значения очень сконцентрированы.
А именно — хоть (как, собственно, и для функции x_1) максимальное от минимального может отличаться на 2 (на диаметр сферы), на 95% площади принимаются значения, отличающиеся друг от друга на const/sqrt{n} (и на 99%, и на 99.9%, вопрос только в константе).
А именно — хоть (как, собственно, и для функции x_1) максимальное от минимального может отличаться на 2 (на диаметр сферы), на 95% площади принимаются значения, отличающиеся друг от друга на const/sqrt{n} (и на 99%, и на 99.9%, вопрос только в константе).
Victor Kleptsyn
М
20:43
Математические байки
Так что мера получается сконцентрированной, с характерным разбросом порядка 1/\sqrt{n}.
Более того, функция x_1 оказывается, в каком-то смысле [я тут чуть-чуть привираю — но чуть ниже уточню], "самым разбросанным" примером.
Более того, функция x_1 оказывается, в каком-то смысле [я тут чуть-чуть привираю — но чуть ниже уточню], "самым разбросанным" примером.
Victor Kleptsyn
М
20:45
Математические байки
Удивительным образом, увидеть это удаётся очень "дёшево". А именно — давайте возьмём медианное значение функции, ту поверхность уровня, которая делит сферу на две части равной площади.
Victor Kleptsyn
М
20:45
Математические байки
И будем от него отходить вверх и вниз и смотреть, как "ужимаются" области {x: f(x)>a} и {x: f(x)<a} соответственно.
Victor Kleptsyn
М
20:49
Математические байки
Поскольку функция 1-липшицева — скорость ужимания не меньше, чем площадь "поверхности уровня" {f(x)=a}. Потому что если мы возьмём \eps-окрестность этой поверхности — то значения в ней в силу 1-липшицевости не выходят за предел [a-\eps, a+\eps]. Так что при переходе от {f(x)>a} к {f(x)>a+\eps} мы, например, смотрящую "внутрь" часть этой \eps-окрестности теряем, а у неё объём это примерно площадь {f(x)=a}, умноженная на \eps ("площадь основания на высоту").
Victor Kleptsyn
М
20:50
Математические байки
А площадь поверхности {f(x)=a} можно сравнить с отсекаемым ею объёмом {f(x)>a} — и изопериметрическое неравенство скажет, что нельзя отрезать "большой" объём маленькой площадью.
Victor Kleptsyn
М
20:51
Математические байки
Так что — если мы знаем, как устроено изопериметрическое неравенство для многомерной сферы (чего я, формально говоря, не сказал, но скажу сейчас, что с этим всё хорошо), то мы сможем сказать, что отрезаемый объём будет убывать быстро.
Victor Kleptsyn
М
20:52
Математические байки
Более того, на самом деле на сфере (что очень естественно) наибольший объём, который можно отрезать данной площадью, это "полярная шапка".
Victor Kleptsyn
М
20:52
Математические байки
Поэтому самое медленное убывание, которое бывает, будет как раз для функции x_1. А для неё мы знаем, что даже она сконцентрирована с разбросом ~1/\sqrt{n}. Ура, победа!
Victor Kleptsyn
М
20:53
Математические байки
[И это как раз то место, где я не сильно, но заметно, привираю, путая расстояния "в R^n" и "по поверхности сферы". Чтобы мои слова стали совсем правдой, нужно брать расстояния по поверхности, произнести слова "риманова метрика", и брать функцию arcsin x_1. Те, кого они не пугают — вот после этого всё совсем почти честно]
Victor Kleptsyn
М
20:56
Математические байки
In reply to this message
С другой стороны, возвращаясь, — хоть рассуждение для разброса мы закончили, вместо явного счёта сказав, что "широта" arcsin x_1 это самая разбросанная функция — вообще-то нам достаточно было бы иметь "хорошее" изопериметрическое неравенство (какое максимальное отношение площади поверхности к ограничиваемому ей объёму). Нужно было только его получить/написать.
Victor Kleptsyn
М
20:56
Математические байки
Константа, которую можно в нём поставить, называется константой Чигера —
https://en.wikipedia.org/wiki/Cheeger_constant#Definition (и, кстати, есть она и для графов — https://ru.wikipedia.org/wiki/Константа_Чигера_(теория_графов) )
https://en.wikipedia.org/wiki/Cheeger_constant#Definition (и, кстати, есть она и для графов — https://ru.wikipedia.org/wiki/Константа_Чигера_(теория_графов) )
Victor Kleptsyn
М
20:56
Математические байки
И её в каких-то случаях получается проконтролировать — и как только мы знаем, что она большая, это и гарантирует концентрацию меры (а также большое первое собственное значение оператора Лапласа и потому "быстрое" расползание случайного блуждания).
Victor Kleptsyn
13 December 2019
М
19:10
Математические байки
In reply to this message
Кстати. Из всё того же многомерного гауссового распределения хорошо получается формула для площади поверхности единичной сферы (и объёма единичного шара) в n-мерном пространстве.
Victor Kleptsyn
М
19:14
Математические байки
Потому что — давайте рассмотрим его плотность в R^n. Только, для простоты счёта, растянем всё в корень из двойки раз. Тогда плотность по одной координате будет просто e^{-x^2}, делённой (нормировка на интеграл 1) на корень из π.
Victor Kleptsyn
М
19:14
Математические байки
А совместная —
\rho(x_1,\dots,x_n) = \frac{1}{\sqrt{π}^n} \exp(-x_1^2-\dots-x_n^2),
\rho(x_1,\dots,x_n) = \frac{1}{\sqrt{π}^n} \exp(-x_1^2-\dots-x_n^2),
Victor Kleptsyn
М
М
19:17
Математические байки
Эта плотность сферически симметрична. И интеграл от неё равен 1 (это же плотность вероятностного распределения). Но давайте его найдём "в сферических координатах" — а точнее, просто порежем всё пространство на "сферические слои".
Если мы возьмём разницу шаров с радиусами r и r+dr, то её объём примерно равен c_n r^{n-1} dr, где c_n — площадь поверхности единичной сферы в R^n.
Если мы возьмём разницу шаров с радиусами r и r+dr, то её объём примерно равен c_n r^{n-1} dr, где c_n — площадь поверхности единичной сферы в R^n.
Victor Kleptsyn
М
19:23
Математические байки
А подынтегральная функция на таком слое равна
π^{-n/2} exp(-r^2). Поэтому интеграл от плотности равен интегралу от c_n r^{n-1}* π^{-n/2} exp(-r^2) dr,
π^{-n/2} exp(-r^2). Поэтому интеграл от плотности равен интегралу от c_n r^{n-1}* π^{-n/2} exp(-r^2) dr,
Victor Kleptsyn
М
М
19:30
Математические байки
А сделав в этом интеграле замену R=r^2, и вынеся константу, мы получим как раз ту самую гамма-функцию Эйлера, которая обобщает факториал:
Victor Kleptsyn
М
М
19:38
Математические байки
Ну вот мы и получили (раз интеграл должен равняться единице), что
c_n Г(n/2) /(2 π^{n/2}) = 1,
откуда
c_n = (2 π^{n/2}) / Г(n/2).
c_n Г(n/2) /(2 π^{n/2}) = 1,
откуда
c_n = (2 π^{n/2}) / Г(n/2).
Victor Kleptsyn
М
М
19:40
Математические байки
А объём единичного шара, соответственно, в n раз меньше (можно сказать, "потому что пирамида из центра", а можно проинтегрировать r^{n-1} и получить r^n/n):
Victor Kleptsyn
М
М
19:42
Математические байки
И вот в этом виде — "π в степени n/2, поделить на n/2 факториал" — я эту формулу когда-то давно узнал, и доказывал индукцией по отдельности для чётных и для нечётных n.
А рассуждение с гауссовой плотностью (объясняющее, почему чётные и нечётные n так хорошо объединились в одну формулу) узнал только гораздо позднее...
А рассуждение с гауссовой плотностью (объясняющее, почему чётные и нечётные n так хорошо объединились в одну формулу) узнал только гораздо позднее...
Victor Kleptsyn
М
19:54
Математические байки
Ну и в завершение — вспомнил я эту формулу тут совершенно не случайно. Потому что если мы захотим посмотреть, как устроено изопериметрическое неравенство на единичной сфере в R^n — какое наименьшее отношение площади к отсекаемому ею объёму (считая, что отсекается та часть, которая меньше половины сферы), то не очень сложно поверить, что это будет как раз отношением для экватора.
Victor Kleptsyn
М
19:54
Математические байки
А тогда оно равно c_{n-1}/(c_n/2). То есть мы видим отношение гамма-функций в точках, отличающихся на (1/2). Но раз Г(m+1)=mГ(m), то очень естественно ожидать, что отношение Г(m+1/2) и Г(m) будет вести себя, как корень из m.
Victor Kleptsyn
М
19:55
Математические байки
Ну и, соответственно, изопериметрическая константа для n-мерной сферы ведёт себя, как корень из n/2 (ибо там половинный аргумент).
Victor Kleptsyn
М
19:57
Математические байки
In reply to this message
Что как раз и соответствует тому, что x_1 имеет разброс порядка 1/sqrt{n} (у соответствующего дифференциального уравнения решением будет экспонента с изопериметрической константой в показателе).
Victor Kleptsyn
14 December 2019
М
21:09
Математические байки
Начиная рассказ про асимптотическую комбинаторику, я надеялся ацтекский бриллиант проскочить быстро, и перейти к другим красивым картинкам, а в результате там надолго застрял. Так что давайте я волевым решением перейду к другому, менее известному примеру — Random Sorting Networks. А потом вернусь и доскажу остальное.
Итак, Random Sorting Networks. Допустим, что у нас в ряд выстроено n тяжёлых чемоданов. Но мы вдруг обнаружили, что нужно их переставить в обратном порядке. А единственная операция, которая нам доступна, это взять два соседних чемодана, и поменять их местами.
Сколько нам понадобится операций? Несложно видеть, что минимум n(n-1)/2, число беспорядков.
Потому что в лучшем случае каждая операция уменьшает число беспорядков на 1 — ну а отсортировать за такое число действий можно, например, "пузырьком".
Итак, Random Sorting Networks. Допустим, что у нас в ряд выстроено n тяжёлых чемоданов. Но мы вдруг обнаружили, что нужно их переставить в обратном порядке. А единственная операция, которая нам доступна, это взять два соседних чемодана, и поменять их местами.
Сколько нам понадобится операций? Несложно видеть, что минимум n(n-1)/2, число беспорядков.
Потому что в лучшем случае каждая операция уменьшает число беспорядков на 1 — ну а отсортировать за такое число действий можно, например, "пузырьком".
Victor Kleptsyn
М
21:10
Математические байки
С другой стороны, число способов отсортировать чемоданы ровно за это число операций больше одного. Из простейшего — можно запустить сортировку "пузырьком" начиная с 1, можно, начиная с n, можно их чередовать, но даже это только начало. А на самом деле их очень и очень много. И да, вы правильно догадались — давайте из них выберем один равновероятным образом.
Victor Kleptsyn
М
21:10
Математические байки
Как выбрать равновероятно — отдельная красивая история: их столько же, сколько способов получить диаграмму Юнга в форме равнобедренного прямоугольного треугольника, добавляя к пустой диаграмме по одной клетке за раз. (Это называется Edelman-Greene's bijection.) Но туда мы сейчас не пойдём.
Victor Kleptsyn
М
21:11
Математические байки
Так вот — давайте посмотрим на случайно выбранную сортировку, когда n достаточно большое. Вот, взятый из статьи Angel, Holroyd, Romik, Virag, "Random Sorting Networks" ( https://www.sciencedirect.com/science/article/pii/S0001870807001545 ) пример для n=6:
Victor Kleptsyn
М
21:13
Математические байки
Тут выделена траектория, по которой движется чемодан номер 3, и отмечены места, где мы выполняли нашу операцию. Но пока ничего красивого не видно; это потому что n у ещё маленькое!
А вот такая у них получается красивая картина, если взять n=2000, и нарисовать (в соответствующем масштабе по осям) траектории отдельных чемоданов —
А вот такая у них получается красивая картина, если взять n=2000, и нарисовать (в соответствующем масштабе по осям) траектории отдельных чемоданов —
Victor Kleptsyn
М
21:13
Математические байки
Правда ведь, напоминает синусоиды?
Victor Kleptsyn
М
21:15
Математические байки
А ещё можно посмотреть на то, как будут устроены графики перестановок (при фиксированном моменте времени, какой чемодан на каком месте стоит). Вот, к примеру (опять из той же статьи) график перестановки, которая наблюдается после половины всех операций:
Victor Kleptsyn
М
21:17
Математические байки
Явно проглядывает круг — но при этом плотность ближе к краям, так, как если бы это была равномерная мера на сфере в трёхмерном пространстве (x,y,z) — которую спроецировали на плоскость (x,y).
Victor Kleptsyn
М
21:19
Математические байки
А что будет в другие моменты времени? Естественно считать параметром t долю от общего числа N выполненных операций; и вот картинка опять же из их работы —
Victor Kleptsyn
М
21:24
Математические байки
Начальный и конечный момент времени это начальное и итоговое расположение чемоданов, у которых графики — прямые. А в промежуточные моменты времени видны эллипсы — а синим показаны полученные уже тогда (11 лет назад, препринт ещё 2006-го — https://arxiv.org/abs/math/0609538v1 ) оценки.
Victor Kleptsyn
М
21:26
Математические байки
In reply to this message
Собственно — вот гипотезы из той работы, как раз это и утверждающие:
Victor Kleptsyn
М
21:28
Математические байки
Мера, как при проекции —
Victor Kleptsyn
М
21:34
Математические байки
Кстати — если рисовать гистограмму того, сколько операций было произведено в такое-то время в таком-то месте, то тоже получается красивая картина:
Victor Kleptsyn
М
21:35
Математические байки
(иллюстрация из всё той же статьи.)
Ну и оттуда же —
Ну и оттуда же —
Victor Kleptsyn
М
21:37
Математические байки
Но ещё интересная история тут — это появление перестановочного многогранника, или пермутоэдра. А именно, давайте посмотрим на обратное отображение после m операций, то есть на набор "на каком месте стоит первый чемодан, на каком второй, ..., как каком n-й".
Это — перестановка, так что в этом векторе каждое из чисел 1,2,...,n встречается по одному разу. При этом одна операция меняет два соседних чемодана — так что какие-то два числа m и m+1 в этом векторе поменяются местами.
Это — перестановка, так что в этом векторе каждое из чисел 1,2,...,n встречается по одному разу. При этом одна операция меняет два соседних чемодана — так что какие-то два числа m и m+1 в этом векторе поменяются местами.
Victor Kleptsyn
М
21:40
Математические байки
И это — переход из одной перестановки в другую на наименьшее возможное расстояние (корень из двух).
Так вот — выпуклый многогранник, вершины которого это всевозможные перестановки вектора (1,2,...,n), называется пермутоэдром, или перестановочным многогранником. Очевидно, что все эти точки лежат в одной плоскости "сумма координат равна 1+...+n", и на одной сфере "сумма квадратов координат равна 1^2+...+n^2".
Так вот — выпуклый многогранник, вершины которого это всевозможные перестановки вектора (1,2,...,n), называется пермутоэдром, или перестановочным многогранником. Очевидно, что все эти точки лежат в одной плоскости "сумма координат равна 1+...+n", и на одной сфере "сумма квадратов координат равна 1^2+...+n^2".
Victor Kleptsyn
М
21:41
Математические байки
А синусоиды, что всплыли выше, оказываются связанными с дугами большого круга — но это тот момент, когда я хочу сделать паузу до следующего раза.
Victor Kleptsyn
16 December 2019
М
17:36
Математические байки
Раз уж всё равно сделана пауза — давайте я расскажу пару коротких баек.
Victor Kleptsyn
М
17:36
Математические байки
Первая — более стандартная, но кажется, не совсем общеизвестная, про чётности перестановок.
Обычно определение чётности перестановки f даётся как чётность числа беспорядков (т.е. пар i<j, для которых f(i)>f(j)) — после чего проверяется, что это же чётность числа транспозиций, в произведение которых f раскладывается.
Обычно определение чётности перестановки f даётся как чётность числа беспорядков (т.е. пар i<j, для которых f(i)>f(j)) — после чего проверяется, что это же чётность числа транспозиций, в произведение которых f раскладывается.
Victor Kleptsyn
М
17:37
Математические байки
Что можно проверить напрямую (взять транспозицию, посмотреть, какие беспорядки она добавляет, какие убирает, и что чётность в итоге всегда меняется), но это немного муторно.
Victor Kleptsyn
М
17:37
Математические байки
А гораздо проще будет сначала рассмотреть разложение f в произведение не абы каких транспозиций, а только транспозиций соседних элементов (i,i+1).
Тогда умножение на такую транспозицию меняет число беспорядков ровно на 1 — как раз на пару (i,i+1).
Тогда умножение на такую транспозицию меняет число беспорядков ровно на 1 — как раз на пару (i,i+1).
Victor Kleptsyn
М
17:38
Математические байки
И поэтому чётность числа беспорядков у f совпадает с чётностью числу транспозиций вида (i,i+1), в произведение которых f раскладывается.
Значит, есть отображение sign(f) из перестановок в {1,-1}, которое корректно определено (ибо определение через беспорядки) и при этом гомоморфизм (ибо определение через чётность числа сомножителей).
Значит, есть отображение sign(f) из перестановок в {1,-1}, которое корректно определено (ибо определение через беспорядки) и при этом гомоморфизм (ибо определение через чётность числа сомножителей).
Victor Kleptsyn
М
17:39
Математические байки
Остаётся проверить, что любая транспозиция нечётна — что проще всего увидеть, сказав, что любая транспозиция сопряжена транспозиции (1,2):
(i,j)=g*(1,2)*g^{-1},
где g — любая перестановка, такая, что g(i)=1, g(j)=2.
(Кстати: вот понимание, что "сопряжение отображением g это просто замена координат y=g(x)", каюсь, до меня в своё время тоже довольно медленно доходило...)
Ну а в g и в g^{-1} чётность числа транспозиций (i,i+1) одинаковая — так что всего число таких транспозиций в (i,j) нечётно. (Да, конечно, можно просто посчитать беспорядки. Но хотелось рассуждения "без единой выкладки".)
(i,j)=g*(1,2)*g^{-1},
где g — любая перестановка, такая, что g(i)=1, g(j)=2.
(Кстати: вот понимание, что "сопряжение отображением g это просто замена координат y=g(x)", каюсь, до меня в своё время тоже довольно медленно доходило...)
Ну а в g и в g^{-1} чётность числа транспозиций (i,i+1) одинаковая — так что всего число таких транспозиций в (i,j) нечётно. (Да, конечно, можно просто посчитать беспорядки. Но хотелось рассуждения "без единой выкладки".)
Victor Kleptsyn
М
17:39
Математические байки
Всё!
Victor Kleptsyn
М
17:40
Математические байки
===
Вторая байка — про теорию вероятностей. Вот тут — https://avva.livejournal.com/3242116.html , https://blog.tanyakhovanova.com/2019/11/my-new-favorite-probability-puzzle/ — обсуждается такая задача. Пусть два игрока, Алиса и Боб, одновременно и независимо играют на деньги с одинаковой начальной суммой в $100, каждую минуту ставя по доллару. Но у Алисы вероятность выигрыша 51%, а у Боба 49%. Известно, что в итоге оба разорились (остались без денег и прекратили игру); _при этом условии_ про кого более вероятно, что он разорился первым?
Вторая байка — про теорию вероятностей. Вот тут — https://avva.livejournal.com/3242116.html , https://blog.tanyakhovanova.com/2019/11/my-new-favorite-probability-puzzle/ — обсуждается такая задача. Пусть два игрока, Алиса и Боб, одновременно и независимо играют на деньги с одинаковой начальной суммой в $100, каждую минуту ставя по доллару. Но у Алисы вероятность выигрыша 51%, а у Боба 49%. Известно, что в итоге оба разорились (остались без денег и прекратили игру); _при этом условии_ про кого более вероятно, что он разорился первым?
Victor Kleptsyn
М
17:40
Математические байки
Spoiler alert: я собираюсь обсуждать (неожиданный) ответ, если вдруг вы эту задачу не решали, она очень стоит того, чтобы над ней подумать.
Victor Kleptsyn
М
17:41
Математические байки
Ответ — равновероятно. Более того, оказывается, что процесс игры Алисы _при условии_ того, что она в конце концов разоряется, такой же, как процесс игры Боба. И это, мне кажется, удивительно!
Victor Kleptsyn
М
17:41
Математические байки
Давайте посмотрим, как этот процесс устроен. Для начала найдём вероятности r_n того, что Алиса разоряется, имея в начале n долларов.
r_0=1 (ибо тут уже всё).
Достаточно естественно (хотя это и надо доказывать — но мы в это поверим), что r_n<1 при всех n>0: шанс не разориться (а получить асимптотически-линейный рост) у Алисы есть, если у неё ещё осталось, на что играть.
r_0=1 (ибо тут уже всё).
Достаточно естественно (хотя это и надо доказывать — но мы в это поверим), что r_n<1 при всех n>0: шанс не разориться (а получить асимптотически-линейный рост) у Алисы есть, если у неё ещё осталось, на что играть.
Victor Kleptsyn
М
17:42
Математические байки
Теперь, если Алиса начинает играть с n долларами, её шанс разориться складывается из вероятности выиграть первую ставку и разориться после того, и проиграть и разориться после того:
r_n = p r_{n+1} + q r_{n-1},
где p=0.51 — её вероятность выигрыша.
r_n = p r_{n+1} + q r_{n-1},
где p=0.51 — её вероятность выигрыша.
Victor Kleptsyn
М
17:43
Математические байки
Это — линейное рекуррентное соотношение, и его решениями оказываются линейные комбинации геометрических прогрессий со знаменателями — корнями характеристического уравнения*; в данном случае — это уравнение px^2-x+q=0.
*) когда кратных корней нет; иначе там (в общей науке линейных рекуррентных соотношений) появляются "квазимногочлены" — произведения многочленов на экспоненты.
*) когда кратных корней нет; иначе там (в общей науке линейных рекуррентных соотношений) появляются "квазимногочлены" — произведения многочленов на экспоненты.
Victor Kleptsyn
М
17:43
Математические байки
Один корень у этого уравнения — 1, отвечающего решению-константе. Собственно, если бы p было меньше 1/2 (а мы ещё нигде p>1/2 не использовали), то мы этот корень и должны увидеть: вероятность разорения в этом случае — тождественная единица.
Victor Kleptsyn
М
17:44
Математические байки
А второй (например, из теоремы Виета, чтобы долго не считать) x=q/p.
Кстати, в качестве ответвления: случай честной монеты, p=q=1/2, это как раз случай кратного корня, и решения уравнения r_{n+1}-2r_n+r_{n-1}=0 это в точности все арифметические прогрессии. Но поскольку r_n это вероятности, такая арифметическая прогрессия остаётся на [0,1] при всех n>0, а ограниченная арифметическая прогрессия — константа. Значит, r_n=1 — игрок с честной монетой тоже разоряется с вероятностью 1 ("случайное блуждание на прямой возвратно"), и такое рассуждение — один из способов это увидеть.
Кстати, в качестве ответвления: случай честной монеты, p=q=1/2, это как раз случай кратного корня, и решения уравнения r_{n+1}-2r_n+r_{n-1}=0 это в точности все арифметические прогрессии. Но поскольку r_n это вероятности, такая арифметическая прогрессия остаётся на [0,1] при всех n>0, а ограниченная арифметическая прогрессия — константа. Значит, r_n=1 — игрок с честной монетой тоже разоряется с вероятностью 1 ("случайное блуждание на прямой возвратно"), и такое рассуждение — один из способов это увидеть.
Victor Kleptsyn
М
17:45
Математические байки
В нашем случае p>1/2 — не очень сложно поверить, что r_n будет стремиться к 0 с ростом n: чем больше у Алисы начальный запас денег, тем меньше её шанс разориться.
Victor Kleptsyn
М
17:45
Математические байки
Но раз r_n=a*1+b*x^n, то a=0, а из r_0=1 тогда следует b=1.
Так что вероятность разорения Алисы — это просто геометрическая прогрессия: r_n=x^n=(q/p)^n.
Так что вероятность разорения Алисы — это просто геометрическая прогрессия: r_n=x^n=(q/p)^n.
Victor Kleptsyn
М
17:47
Математические байки
Осталось понять, как при условии "Алиса разорилась" выглядит процесс её игры. Если в какой-то момент у неё n долларов, то шансы перейти в (n+1) и в (n-1) за один шаг равны соответственно p*r_{n+1}/r_n и q*r_{n-1}/r_n (а то, что их сумма равна 1 — это и было наше уравнение).
Victor Kleptsyn
М
М
17:47
Математические байки
И поэтому эти вероятности равны
p*(q/p)=q и q*(p/q)=p соответственно — то есть игра Алисы _при условии разорения_ стала игрой Боба!
p*(q/p)=q и q*(p/q)=p соответственно — то есть игра Алисы _при условии разорения_ стала игрой Боба!
Victor Kleptsyn
М
17:51
Математические байки
И это хорошее место, чтобы чуть-чуть задуматься, "а почему". А есть ли хорошее объяснение, что вероятность разорения оказалась именно геометрической прогрессией? (Так-то мы сослались на рекуррентные уравнения, формально говоря, задействовав линейную алгебру... а проще можно?)
И ещё — если Алиса начинает с $n, то процесс её игры при условии достижения $0 (разорения) будет таким же, как и при условии достижения любого фиксированного уровня $k с k<n: это та же игра, но Алиса с самого начала откладывает $k "на дорогу домой" и на них не играет. То есть все такие условия приводят к одинаковому условному процессу. А почему?
И ещё — если Алиса начинает с $n, то процесс её игры при условии достижения $0 (разорения) будет таким же, как и при условии достижения любого фиксированного уровня $k с k<n: это та же игра, но Алиса с самого начала откладывает $k "на дорогу домой" и на них не играет. То есть все такие условия приводят к одинаковому условному процессу. А почему?
Victor Kleptsyn
М
18:01
Математические байки
На самом деле это один и тот же вопрос, и на него есть разумный ответ. А именно — с одной стороны, чтобы разориться, Алисе нужно в какой-то момент иметь на руках $(n-1). С другой, после того, как Алиса эту сумму получила, её игра не зависит от того, что было раньше — так что
r_n = (вероятность от $n когда-нибудь достигнуть $n-1) * r_{n-1}.
И если обозначить эту вероятность "отступить на доллар" через x, то вот мы и получаем геометрическую прогрессию.
r_n = (вероятность от $n когда-нибудь достигнуть $n-1) * r_{n-1}.
И если обозначить эту вероятность "отступить на доллар" через x, то вот мы и получаем геометрическую прогрессию.
Victor Kleptsyn
М
18:04
Математические байки
Ну и наконец — отсюда же видно, что условия "разориться" и "когда-нибудь достигнуть $(n-1)" имеют на первый шаг (и вообще на все шаги до достижения $(n-1)) одинаковый эффект: потому что всё, что будет, начиная с $(n-1), от того, что было до, не зависит.
Victor Kleptsyn
М
18:04
Математические байки
Ну и на этом я на сегодня прекращаю дозволенные речи.
Victor Kleptsyn
15 January 2020
М
13:32
Математические байки
Запоздалое — с Новым Годом!
Сегодняшняя байка — рассказ о подстановочных словах.
Давайте зададим вот такое отображение F на словах из букв А и Б: заменим одновременно каждую букву А на слово АБ, а каждую букву Б на А.
Например, F(БАА)=ААБАБ.
И будем это отображение итерировать, начав с однобуквенного слова w_1=А: рассмотрим последовательность его образов w_n=F(w_{n-1}).
Что у нас получится?
Сегодняшняя байка — рассказ о подстановочных словах.
Давайте зададим вот такое отображение F на словах из букв А и Б: заменим одновременно каждую букву А на слово АБ, а каждую букву Б на А.
Например, F(БАА)=ААБАБ.
И будем это отображение итерировать, начав с однобуквенного слова w_1=А: рассмотрим последовательность его образов w_n=F(w_{n-1}).
Что у нас получится?
Victor Kleptsyn
М
13:32
Математические байки
Вот первые несколько образов:
w_1=А
w_2=АБ
w_3=АБА
w_4=АБААБ
w_5=АБААБАБА
Явно видно, что следующее слово продолжает предыдущее — что мгновенно доказывается по индукции. Значит, есть одно бесконечное слово, у которого все эти слова являются началами.
Это слово
w = АБААБАБААБААБАБААБАБА...
называется словом Фибоначчи.
А что о нём можно сказать?
w_1=А
w_2=АБ
w_3=АБА
w_4=АБААБ
w_5=АБААБАБА
Явно видно, что следующее слово продолжает предыдущее — что мгновенно доказывается по индукции. Значит, есть одно бесконечное слово, у которого все эти слова являются началами.
Это слово
w = АБААБАБААБААБАБААБАБА...
называется словом Фибоначчи.
А что о нём можно сказать?
Victor Kleptsyn
М
13:33
Математические байки
Оказывается, очень много — а пройдя по этой дороге чуть-чуть дальше, можно получить вот такую красивую картинку, фрактал Рози
(picture credit: А. Я. Канель-Белов, И. В. Митрофанов):
(picture credit: А. Я. Канель-Белов, И. В. Митрофанов):
Victor Kleptsyn
М
13:42
Математические байки
Но это будет итоговая "светлая цель", к которой мы дойдём, а пока давайте начнём с совсем простого: посчитаем буквы. (Почему? Да просто потому, что если вдруг есть непонятный объект, так давайте его измерим, насколько получится, вдруг что интересное найдём.)
Victor Kleptsyn
М
13:42
Математические байки
In reply to this message
Сколько букв в словах w_1, w_2, w_3,...? Посчитав, видимо знакомую нам последовательность
1, 2, 3, 5, 8, ...
А сколько по отдельности букв А и Б?
1, 2, 3, 5, 8, ...
А сколько по отдельности букв А и Б?
Victor Kleptsyn
М
13:43
Математические байки
Сразу видны числа Фибоначчи; а как бы это доказать?
Мы знаем, что следующее слово продолжает предыдущее, не получится ли что-то увидеть из этого?
Давайте посмотрим, что остаётся, если из нового слова убрать идущее перед ним:
Мы знаем, что следующее слово продолжает предыдущее, не получится ли что-то увидеть из этого?
Давайте посмотрим, что остаётся, если из нового слова убрать идущее перед ним:
Victor Kleptsyn
М
13:43
Математические байки
Невооружённым глазом видно, что остаётся то слово, что было до того. То есть
w_{n+1} = w_n w_{n-1}.
И когда это написано, доказательство тоже мгновенно проводится по индукции, из базы либо АБА= АБ А,
либо даже АБ= А Б с формальным добавлением w_0=Б.
w_{n+1} = w_n w_{n-1}.
И когда это написано, доказательство тоже мгновенно проводится по индукции, из базы либо АБА= АБ А,
либо даже АБ= А Б с формальным добавлением w_0=Б.
Victor Kleptsyn
М
14:33
Математические байки
In reply to this message
Теперь понятно, почему бесконечное слово называют "словом Фибоначчи": последовательность слов, которая к нему приводит, получается как раз из Фибоначчи-подобного соотношения.
Но давайте продолжим нашу деятельность по счёту букв. А именно, давайте посмотрим, сколько букв А и Б оказывается среди первых k букв слова Фибоначчи — и отметим соответствующую точку на плоскости (по оси абсцисс отложив буквы А, а по оси ординат буквы Б). Получится этакая "змейка": при добавлении одной буквы мы сдвинемся на расстояние 1.
Но давайте продолжим нашу деятельность по счёту букв. А именно, давайте посмотрим, сколько букв А и Б оказывается среди первых k букв слова Фибоначчи — и отметим соответствующую точку на плоскости (по оси абсцисс отложив буквы А, а по оси ординат буквы Б). Получится этакая "змейка": при добавлении одной буквы мы сдвинемся на расстояние 1.
Victor Kleptsyn
М
14:41
Математические байки
Сразу кажется, что она очень хорошо "выдерживает направление". Кстати, коэффициент наклона того направления, в котором она идёт (если предположить, что он есть) — золотое сечение, точнее, обратная к нему величина 1/Ф (букв А больше, а традиционно Ф^2=Ф+1).
Потому что отношение последовательных чисел Фибоначчи стремится к золотому сечению, а мы знаем, что в подслове w_n количество букв А и Б это последовательные числа Фибоначчи.
Потому что отношение последовательных чисел Фибоначчи стремится к золотому сечению, а мы знаем, что в подслове w_n количество букв А и Б это последовательные числа Фибоначчи.
Victor Kleptsyn
М
14:43
Математические байки
Но буквально так мы что-то говорим только про слова w_n — а они становятся всё длиннее и длиннее, и формально мы пока ничего не сказали про подслова длиной между |w_n| и |w_{n+1}|.
Victor Kleptsyn
М
17:16
Математические байки
И всё равно; давайте посмотрим, насколько хорошо точки ложатся на какую-то прямую — попробовав заключить их в полосу. Оказывается, что это полоса вполне небольшого размера:
Victor Kleptsyn
М
17:17
Математические байки
А прямые, которые её ограничивают — проходят через точки (-1,0) и (0,-1); и вся эта змейка, какой бы длины она не была, не выходит за рамки этой весьма неширокой полосы.
Victor Kleptsyn
М
17:17
Математические байки
Но интереснее другое: давайте точки ещё и раскрасим.
Victor Kleptsyn
М
17:18
Математические байки
Если последняя посчитанная буква А — поставим красную точку, если Б — синюю. Вот, что получится:
Victor Kleptsyn
М
17:18
Математические байки
Очень естественно, что красные точки в целом ниже/правее синих. Но что будет, если мы их спроецируем на перпендикулярный отрезок?
Victor Kleptsyn
М
17:19
Математические байки
Окажется, что проекции красных точек заметают один отрезок, проекции синих другой, и эти отрезки не пересекаются.
Victor Kleptsyn
М
17:20
Математические байки
In reply to this message
Теперь уже можно сказать (хотя пока конструкция "повиснет в воздухе"), откуда берётся фрактал Рози, который мы заявили, как цель.
Victor Kleptsyn
М
17:23
Математические байки
А именно — нужно взять другие правила замен, уже из трёх букв:
A -> AB
B -> AC
C -> A
И точно так же много-много раз их применять к исходному слову из одной буквы А. Все получающиеся слова будут префиксами одного и того же слова Трибоначчи
ABACABA...
A -> AB
B -> AC
C -> A
И точно так же много-много раз их применять к исходному слову из одной буквы А. Все получающиеся слова будут префиксами одного и того же слова Трибоначчи
ABACABA...
Victor Kleptsyn
М
17:24
Математические байки
Если посчитать, сколько по отдельности букв A, B и C из первых k букв слова Трибоначчи — получится "змейка", растущая уже в трёхмерном пространстве:
Victor Kleptsyn
М
17:25
Математические байки
И если спроецировать её на перпендикулярную её асимптотическому направлению плоскость, то точки заметут фигуру, которая разделится на проекции красных (А), синих (B) и зелёных (C) точек:
Victor Kleptsyn
М
17:25
Математические байки
Вот это и есть тот самый фрактал Рози.
Victor Kleptsyn
М
17:27
Математические байки
То направление, в котором растёт эта змейка — собственное направление матрицы замен
(1 1 1)
(1 0 0)
(0 1 0),
применение которой пересчитывает буквы A, B и C в исходном слове в количество букв в его образе, с собственным значением, большим 1.
(1 1 1)
(1 0 0)
(0 1 0),
применение которой пересчитывает буквы A, B и C в исходном слове в количество букв в его образе, с собственным значением, большим 1.
Victor Kleptsyn
М
17:29
Математические байки
А два других собственных значения этой матрицы — комплексно-сопряжённые с модулем, меньшим 1. Умножение на них и выступает в качестве подобия, последовательно (и с добавлением сдвигов) превращающего всю проекцию в каждую из трёх частей.
Victor Kleptsyn
М
17:35
Математические байки
Мне остаётся договорить про то, как связано слово Фибоначчи с перекладываниями отрезка и поворотом окружности, но это я сделаю в следующий раз, а пока несколько ссылок:
- записки дубнинского курса о подстановочных словах + картинки: https://www.mccme.ru/dubna/2014/courses/kanel-mitrofanov.htm (ссылки на два PDFа внизу)
- ролик Numberphile примерно об этом же:
https://www.youtube.com/watch?v=fMJflV_GUpU
- дубнинская лекция А. П. Веселова:
http://www.mathnet.ru/php/presentation.phtml?option_lang=rus&presentid=24811
- статья М. Л. Концевича в Кванте —
https://kvant.ras.ru/1985/07/ravnomernye_raspolozheniya.htm
- записки дубнинского курса о подстановочных словах + картинки: https://www.mccme.ru/dubna/2014/courses/kanel-mitrofanov.htm (ссылки на два PDFа внизу)
- ролик Numberphile примерно об этом же:
https://www.youtube.com/watch?v=fMJflV_GUpU
- дубнинская лекция А. П. Веселова:
http://www.mathnet.ru/php/presentation.phtml?option_lang=rus&presentid=24811
- статья М. Л. Концевича в Кванте —
https://kvant.ras.ru/1985/07/ravnomernye_raspolozheniya.htm
Victor Kleptsyn
М
17:36
Математические байки
А на сегодня я на этом прекращаю дозволенные речи...
Victor Kleptsyn
3 February 2020
М
16:03
Математические байки
В прошлый раз я рассказывал о подстановочных словах и о слове Фибоначчи в частности — но совсем не рассказал о связанных с этим квазипериодических паркетах, а это простая и геометрическая история.
Victor Kleptsyn
М
16:03
Математические байки
Давайте проведём в правильном пятиугольнике три диагонали, и посмотрим, какие у нас получатся треугольники:
Victor Kleptsyn
М
16:05
Математические байки
Оба треугольника, и красный, и синий — равнобедренные. Если взять короткую сторону за 1, то у синего стороны — это 1,1,Ф, а у красного — Ф,Ф,1, где Ф — золотое сечение.
Victor Kleptsyn
М
16:06
Математические байки
То, что Ф это именно золотое сечение, несложно увидеть из того, что большой треугольник BCD, который они образуют вместе, подобен синему. И получается (из стороны BD) классическое уравнение Ф^2=Ф+1.
Victor Kleptsyn
М
16:08
Математические байки
Но я не стал бы рассказывать столь классические (пару тысяч лет как) вещи, если бы тут не происходило чего-нибудь более интересного. А именно: пока мы из одного красного и одного синего треугольника сделали треугольник, подобный синему с коэффициентом Ф.
Так вот, из двух красных и одного синего треугольника можно сделать треугольник, подобный красному. С тем же самым коэффициентом подобия!
Так вот, из двух красных и одного синего треугольника можно сделать треугольник, подобный красному. С тем же самым коэффициентом подобия!
Victor Kleptsyn
М
16:10
Математические байки
И увидеть это можно внутри всё того же правильного пятиугольника, проведя ещё одну диагональ (и мысленно сжав всё в Ф раз):
Victor Kleptsyn
М
16:10
Математические байки
(Нижний синий треугольник это уже "меньший красный+меньший синий", и добавление ещё одного "меньшего красного" превращает его обратно в красный)
Victor Kleptsyn
М
16:11
Математические байки
Итак, из синих и красных треугольников можно сделать подобные им и в Ф раз большие синие и красные треугольники.
Victor Kleptsyn
М
16:11
Математические байки
А давайте повторять эту процедуру, например, начиная с одного красного треугольника —
Victor Kleptsyn
М
16:14
Математические байки
И раз красный треугольник был в углу своего образа — то каждый следующий образ (по индукции) продолжает предыдущий.
Victor Kleptsyn
М
16:15
Математические байки
In reply to this message
Точно так же, как образы А при итерации подстановочного отображения продолжали друг друга.
Victor Kleptsyn
М
16:16
Математические байки
И точно так же, как из их итераций в пределе получалось бесконечное (вправо) слово — тут мы получим замощение угла в 36 градусов на плоскости:
Victor Kleptsyn
М
16:19
Математические байки
А объединив 10 таких углов — получим и разбиение всей плоскости.
Victor Kleptsyn
3 February 2020
М
16:20
Математические байки
И получающееся замощение — "квазипериодично". С одной стороны, отношение количеств красных и синих треугольников в больших кусочках этого замощения стремится... конечно же, к золотому сечению Ф.
Victor Kleptsyn
М
16:22
Математические байки
Потому что количество красных и синих треугольников в образе красного или синего треугольника после n замен это пара последовательных чисел Фибоначчи (упражнение: докажите это!)
Victor Kleptsyn
М
16:23
Математические байки
А раз наше замощение режется на красные и синие треугольники — то оно режется и на, скажем, их 5-е образы, в каждом из которых отношение количеств К:С близко к Ф. А если недостаточно близко, то можно резать на 10-е образы, или на 20-е...
Victor Kleptsyn
М
16:23
Математические байки
Поэтому периодичным оно быть не может: Ф иррационально.
Victor Kleptsyn
М
16:25
Математические байки
С другой стороны, любой конечный кусочек замощения, который хоть где-то встречается, встречается достаточно регулярно. Потому что он содержится в образе красного треугольника после какого-то числа n замен, а красные треугольники (а значит, и их образы) "есть везде".
Victor Kleptsyn
М
16:26
Математические байки
Формально — найдётся R, такое, что в любом круге радиуса R найдётся копия n-кратного образа красного треугольника.
Victor Kleptsyn
М
16:30
Математические байки
In reply to this message
Кстати — как можно увидеть из этой картинки, после нескольких (шести, если я не обсчитался) замен мы получаем 10 красных треугольников, образующих круг. Поэтому, применив предыдущее утверждение к n+6 вместо n, можно ещё к этому добавить, что есть не только копия, а копия в любом из 10 возможных поворотов на кратные 36 градусам углы.
Victor Kleptsyn
М
16:32
Математические байки
А вот обладающая таким же свойством мозаика Пенроуза (разбиение плоскости на ромбы двух типов, тоже квазипериодичное):
Victor Kleptsyn
М
16:33
Математические байки
(picture source: Wikipedia, https://en.wikipedia.org/wiki/Penrose_tiling )
Victor Kleptsyn
М
16:43
Математические байки
Ну и, заговорив о квазипериодичных мозаиках, нельзя не упомянуть квазикристаллы. Есть такая наука — кристаллография. Собственно, занимающаяся изучением кристаллов, и недавно отпразновавшая своё столетие. (Кстати — вот этот небольшой мультфильм, который по этому случаю сделали, мне очень нравится: https://www.youtube.com/watch?v=uqQlwYv8VQI )
Интересно, как именно ещё до всяких электронных микроскопов люди сумели "заглянуть" в кристаллическую решётку и измерить её; казалось бы, с нашего "макроскопического" масштаба до отдельных атомов "не дотянуться".
Интересно, как именно ещё до всяких электронных микроскопов люди сумели "заглянуть" в кристаллическую решётку и измерить её; казалось бы, с нашего "макроскопического" масштаба до отдельных атомов "не дотянуться".
Victor Kleptsyn
М
16:45
Математические байки
Берём _моно_кристалл; и светим на него рентгеном. Можно считать, что каждый отдельный атом решётки рассеивает падающее излучение (волну) во все стороны. Но. Атомов-то много. И каждый рассеивает во все стороны.
Victor Kleptsyn
М
16:46
Математические байки
Но фаза при этом может сдвинуться:
Victor Kleptsyn
М
16:47
Математические байки
(image credit: Wikipedia, https://en.wikipedia.org/wiki/Bragg%27s_law )
Victor Kleptsyn
М
16:51
Математические байки
Поэтому в "большинство" направлений в итоге ничего не уйдёт — если хоть один сдвиг фазы не кратен 2\pi, то все атомы изображают из себя лебедя, рака и щуку, и в сумме дают ноль. (Потому что такой сдвиг между атомами решётки можно повторять снова и снова, на то она и решётка, а тогда среднее должно быть инвариантно относительно соответствующего сдвига фазы, и это может быть только тождественный ноль.)
Victor Kleptsyn
М
16:55
Математические байки
Получается условие, что сдвиги фазы все должны быть кратными 2\pi. И в результате мы получаем на плёнке засвеченные отдельные точки — если аккуратно поразбираться, это пересечение некоторой сферы с двойственной решёткой в сопряжённом пространстве, но я не хочу лезть в такие детали; главное — что мы получаем некоторую картину, по которой можно восстановить исходную решётку, но это действие нетривиальное.
Victor Kleptsyn
М
16:56
Математические байки
этот кадр — из мультфильма, что я упоминал; кстати, а вот оттуда же — постановка эксперимента:
Victor Kleptsyn
М
17:14
Математические байки
Так вот, в 1982-м Дэн Шехтман обнаружил симметрию 10 порядка в одном из материалов (правда, там вместо ренгена использовались электроны, поэтому нужно говорить чуть более аккуратно и работать с поверхностью — чего я делать не буду; байка, как-никак). Примерно такую (image credit: wikipedia, https://en.wikipedia.org/wiki/Quasicrystal ) :
Victor Kleptsyn
М
17:15
Математические байки
Но все кристаллографы знали, что симметрии 10 порядка не бывает. Потому что если у решётки есть такая симметрия R, то для самого короткого вектора v решётки вектор v-R(v) будет тоже принадлежать решётке, и будет ещё короче.
Victor Kleptsyn
М
17:20
Математические байки
Так вот — оказалось, что материалы тоже умеют образовывать не только периодические решётки-кристаллы, но и квазипериодические. Как раз такие, как мы видели выше — а-ля мозаика Пенроуза.
И это открытие, с одной стороны, Шехтману далось с большим боем (включая то, как ему советовали "перечитать учебник" и произносившееся в его сторону "Нет никаких квазикристаллов, есть только квазиучёные"), а с другой — в 2011-м принесло ему Нобелевскую премию.
И это открытие, с одной стороны, Шехтману далось с большим боем (включая то, как ему советовали "перечитать учебник" и произносившееся в его сторону "Нет никаких квазикристаллов, есть только квазиучёные"), а с другой — в 2011-м принесло ему Нобелевскую премию.
Victor Kleptsyn
М
17:24
Математические байки
In reply to this message
Если от физики и геометрии вернуться к слову Фибоначчи, то я в прошлый раз обещал перекладывание отрезков и поворот окружности.
Victor Kleptsyn
М
17:27
Математические байки
И мы в прошлый раз (очень естественно) раскрашивали точки в тот цвет, какая последняя буква была написана. Но можно их раскрашивать по тому, какая буква следующая. И получается другая раскраска:
Victor Kleptsyn
М
17:28
Математические байки
С другой разделяющей линией — красные точки теперь сверху:
Victor Kleptsyn
М
17:28
Математические байки
In reply to this message
И проекция теперь выглядит не так, как раньше —
Victor Kleptsyn
М
17:29
Математические байки
То есть "красный" и "синий" интервалы в проекции поменялись местами.
Victor Kleptsyn
М
17:32
Математические байки
С другой стороны, красные точки при таком изменении раскраски сдвигаются на (1,0), потому что в одном случае мы саму "красящую" букву А считаем, в другом нет, а синие на (0,1).
Victor Kleptsyn
М
17:33
Математические байки
С другой стороны, перекладывание двух отрезков это поворот окружности, которая из этих отрезков как из дуг склеивается. И если на всё это внимательно посмотреть (или поверить рассказчику на слово), то получается другое описание слова Фибоначчи.
Victor Kleptsyn
М
17:34
Математические байки
А именно: окружность разбита на красную и синюю дуги с отношением длин Ф:1 —
Victor Kleptsyn
М
17:36
Математические байки
Исходно на ней отмечена точка на границе дуг A и B, и каждый шаг она поворачивается на длину дуги B в положительном направлении. Если на k-м шаге она попадает в дугу А, то мы пишем А, а если в дугу B, то пишем B.
Victor Kleptsyn
М
17:42
Математические байки
Всё хорошо, но пока что это описание исключительно "феноменологическое": мы что-то увидели на первых ~30 итерациях, и сделали из этого какие-то (формально — совершенно не доказанные) выводы.
Victor Kleptsyn
М
17:42
Математические байки
Так вот — как раз поворот окружности это штука, к подстановочному правилу очень хорошо привязываемая.
Victor Kleptsyn
М
17:43
Математические байки
Потому что — давайте смотреть не за всеми итерациями начальной точки, а только за теми, когда она попадает на дугу А.
Victor Kleptsyn
М
17:44
Математические байки
Тогда дуга А разобьётся на две поддуги, А' и B'. Где, стартовав из поддуги B', мы сразу остаёмся в дуге A, а из поддуги A' сначала прыгаем в B, а потом в A:
Victor Kleptsyn
М
17:46
Математические байки
(То, что мы сейчас делаем, называется в теории динамических систем умными словами "отображение первого возвращения", "башня Какутани", и так далее — но это совершенно неважно.)
Victor Kleptsyn
М
17:47
Математические байки
Так вот — склеив дугу А обратно в окружность, мы увидим на ней опять поворот (получившийся из перекладывания отрезков — дуг А' и B'), а восстановление исходного слова по слову в алфавите A' и B' это как раз наши правила подстановки:
"A' означает АB,
B' означает A"
"A' означает АB,
B' означает A"
Victor Kleptsyn
М
17:50
Математические байки
А то, что отношение длин исходных дуг Ф:1, означает, что и отношение длин дуг А' к B' будет Ф:1. Так что картина повторяется снова и снова.
Victor Kleptsyn
М
17:51
Математические байки
In reply to this message
И вот из этого уже можно устроить доказательство — а заодно для других отношений длин возникает цепная дробь, а заодно те самые равномерные размещения, о которых писал Концевич в Кванте и говорил Веселов в Дубне.
Victor Kleptsyn
М
17:53
Математические байки
Ну и на этом, кажется, предыдущее обещание выполнено.
Victor Kleptsyn
М
17:58
Математические байки
Бонусом к сегодняшнему рассказу — несколько фотографий из Warwick University. Который, для простоты навигации, находится в два с половиной раза ближе к Coventry, чем к Warwick-у; не назвали его Coventry University потому, что Coventry University к тому моменту уже был и был достаточно известен.
Victor Kleptsyn
М
18:03
Математические байки
Как написано на табличке-подписи,
"Оригинальная доска объявлений семинаров.
Важный исторический артефакт до-цифровой эры,
ок. 1963"
"Оригинальная доска объявлений семинаров.
Важный исторический артефакт до-цифровой эры,
ок. 1963"
Victor Kleptsyn
М
18:05
Математические байки
Новые семинары можно было вписывать вниз, перематывая бумагу с нижнего рулона на верхний.
Victor Kleptsyn
М
18:07
Математические байки
А вот это — содержимое стоящего рядом шкафа с "интересными объектами":
Victor Kleptsyn
М
18:18
Математические байки
Ну и — здание, где расположен математический факультет, называется в честь его основателя Zeeman building, и там висит его портрет. Но Zeeman не тот, который эффект Зеемана (тот физик, https://ru.wikipedia.org/wiki/%D0%97%D0%B5%D0%B5%D0%BC%D0%B0%D0%BD,_%D0%9F%D0%B8%D1%82%D0%B5%D1%80 ) — а математик (https://en.wikipedia.org/wiki/Christopher_Zeeman )
Victor Kleptsyn
М
18:19
Математические байки
Ну и на этой исторической ноте я на сегодня прекращаю дозволенные речи.
Victor Kleptsyn
9 February 2020
М
17:53
Математические байки
Если вдруг кто-то ещё не видел -- потрясающая задача с сегодняшнего матпраздника:
Victor Kleptsyn
М
17:53
Математические байки
Н
Непрерывное математическое образование 09.02.2020 13:49:56
Можно ли разрезать такого «верблюда» на 3 части и сложить из них квадрат? (Задача Ю.Маркелова с сегодняшнего Матпраздника)
Victor Kleptsyn
17 February 2020
М
21:23
Математические байки
In reply to this message
Вдогонку к моему прошлому рассказу — дополнение от коллег:
Victor Kleptsyn
М
21:25
Математические байки
PV
Polina Vytnova 04.02.2020 09:55:06
Под подписью к фотографии Chr. Zeeman - FRS = fellow Royal Society = Академик РАН
Victor Kleptsyn
М
21:25
Математические байки
PV
Polina Vytnova 04.02.2020 09:56:13
Sir is a Royal title, he received a knighthood in the 1991 Birthday Honours for "mathematical excellence and service to British mathematics and mathematics education"
Victor Kleptsyn
М
21:25
Математические байки
PV
Polina Vytnova 04.02.2020 09:56:26
= премия президента 😊
Victor Kleptsyn
М
21:25
Математические байки
PV
Polina Vytnova 04.02.2020 09:59:27
шкаф с объектами создан Saul Schleimer, https://homepages.warwick.ac.uk/~masgar/talks_and_exhibits.html#art
Victor Kleptsyn
М
21:25
Математические байки
PV
Polina Vytnova 04.02.2020 09:59:38
he also holds art exhibitions
Victor Kleptsyn
М
21:25
Математические байки
PV
Polina Vytnova 04.02.2020 09:59:51
(of math objects)
Victor Kleptsyn
М
21:27
Математические байки
In reply to this message
И эту страничку действительно стоит посмотреть — скажем, там лежат очень красивые слайды про квартику Клейна,
https://homepages.warwick.ac.uk/~masgar/Talks/2015-08-29klein_uiuc.pdf
https://homepages.warwick.ac.uk/~masgar/Talks/2015-08-29klein_uiuc.pdf
Victor Kleptsyn
М
21:28
Математические байки
(Ту же, про которую недавно писали коллеги)
Victor Kleptsyn
М
М
21:29
Математические байки
А ещё — оказывается, каналу "баек" исполнилось уже полгода!
Victor Kleptsyn
М
21:29
Математические байки
И — сегодняшняя байка, которую мне давно хотелось записать, это рассказ про высоты треугольника.
Victor Kleptsyn
М
21:29
Математические байки
Вот есть одна из первых теорем классической геометрии, что высоты треугольника пересекаются в одной точке. Все её знают.
А будет ли она верна в сферической геометрии? Или (для тех, кто с ней знаком) на плоскости Лобачевского?
А будет ли она верна в сферической геометрии? Или (для тех, кто с ней знаком) на плоскости Лобачевского?
Victor Kleptsyn
М
21:31
Математические байки
Оказывается, что — да, будет. На сфере совсем, а на плоскости Лобачевского с одной оговоркой, о которой после.
И у этого факта я знаю два разных объяснения: одно от В. И. Арнольда, и совершенно другое — от А. Г. Хованского.
И у этого факта я знаю два разных объяснения: одно от В. И. Арнольда, и совершенно другое — от А. Г. Хованского.
Victor Kleptsyn
М
21:31
Математические байки
Давайте начнём со случая сферы: пусть на сфере с центром O отмечены три точки A, B и С. Они образуют треугольник — в котором можно проводить высоты AH_A, BH_B, CH_C. И хорошо бы как-то научиться со всем этим работать.
Victor Kleptsyn
М
21:32
Математические байки
(Например, понятно, что если треугольник "маленький", то геометрия там почти евклидова, и высоты "в первом приближении" относительно размеров треугольника должны пересечься в одной точке. Но то в первом приближении, а утверждается-то точное равенство...)
Victor Kleptsyn
М
21:33
Математические байки
Для начала — а что такое прямая на сфере? Это дуга большого круга, сечение сферы плоскостью, проходящей через центр сферы. Иными словами — экватор.
Victor Kleptsyn
М
21:34
Математические байки
А если есть экватор, то есть и полюса — и между парами противоположных точек на сфере ("полюсами") и экваторами, очевидно, есть взаимно-однозначное соответствие (а именно — прямая, проходящая через "полюса", это ортогональное дополнение к плоскости, высекающей экватор).
Victor Kleptsyn
М
21:34
Математические байки
Как устроен полюс P_C, отвечающий "экватору"-дуге AB? Это направление, перпендикулярное плоскости OAB — то есть задаваемое векторным произведением [OAxOB].
Victor Kleptsyn
М
21:35
Математические байки
А чем ещё хороши полюса? Тем, что перпендикуляры к экватору — это меридианы. И все меридианы проходят через полюса!
Точнее, дуга большого круга перпендикулярна экватору тогда и только тогда, когда она проходит через полюс.
Точнее, дуга большого круга перпендикулярна экватору тогда и только тогда, когда она проходит через полюс.
Victor Kleptsyn
М
21:35
Математические байки
То есть высота CH_C — это та же прямая (на сфере), что и CP_C
Victor Kleptsyn
М
21:36
Математические байки
Опять рассматривая уже соответствующий ей полюса, видим, что они лежат на прямой, задаваемой векторным произведением [OCxOH_C]. А раз OH_C пропорционально [OAxOB], то эти полюса высекаются на сфере прямой (в пространстве), задающейся направлением-"двойным" произведением:
[OCx[OAxOB]].
[OCx[OAxOB]].
Victor Kleptsyn
М
21:38
Математические байки
Теперь, три "экватора" пересекаются в одной точке тогда и только тогда, когда у содержащих их плоскостей в R^3 есть нетривиальное пересечение — и это равносильно тому, что прямые-ортогональные дополнения к этим плоскостям лежат в одной плоскости.
Victor Kleptsyn
М
21:39
Математические байки
(Возможно, вам уже попадалось аналогичное утверждение из полюс-полярной двойственности: три прямые пересекаются в одной точке тогда и только тогда, когда их полюса лежат на одной прямой; это, конечно, о том же.)
Victor Kleptsyn
М
21:41
Математические байки
Итак, нам нужно проверить, что три вектора -- "двойные" произведения
[OCx[OAxOB]], [OAx[OBxOC]] и [OBx[OCxOA]] --
лежат в одной плоскости. Но тождество Якоби — собственно, чуть ли не самое важное тождество для векторных произведений, а потом и для алгебр Ли — утверждает, что их сумма равна нулю!
[OCx[OAxOB]], [OAx[OBxOC]] и [OBx[OCxOA]] --
лежат в одной плоскости. Но тождество Якоби — собственно, чуть ли не самое важное тождество для векторных произведений, а потом и для алгебр Ли — утверждает, что их сумма равна нулю!
Victor Kleptsyn
М
21:41
Математические байки
Всё, конец доказательства: три полюса лежат на одной дуге большого круга — три высоты пересекаются в одной точке.
Victor Kleptsyn
М
21:43
Математические байки
Это — "Арнольдовское" рассуждение.
А вот второе, совершенно другое.
А вот второе, совершенно другое.
Victor Kleptsyn
М
21:43
Математические байки
Давайте возьмём на сфере какую-нибудь точку P, проведём в ней касательную плоскость π и на эту плоскость всю картинку центрально спроецируем.
Victor Kleptsyn
М
21:45
Математические байки
Тогда дуги большого круга, которые высекаются на сфере проходящими через её центр O плоскостями, перейдут в прямые, высекаемые этими же плоскостями на π.
Victor Kleptsyn
М
21:46
Математические байки
Но вот с углами будет твориться тихий ужас. И когда я в первый раз услышал это начало рассуждения, я не мог поверить, что тут что-то можно так сделать. Ан нет, можно.
Victor Kleptsyn
М
21:47
Математические байки
Дело в том, что прямые углы в одной ситуации сохраняются.
Лемма. Две дуги большого круга, одна из которых проходит через точку P, перпендикулярны на сфере тогда и только тогда, когда перпендикулярны на плоскости прямые, являющиеся их центральными проекциями.
Лемма. Две дуги большого круга, одна из которых проходит через точку P, перпендикулярны на сфере тогда и только тогда, когда перпендикулярны на плоскости прямые, являющиеся их центральными проекциями.
Victor Kleptsyn
М
21:48
Математические байки
И доказательство у этого очень простое. Дело в том, что быть перпендикулярным прямой m — это всё равно, что сохраняться симметрией относительно этой прямой.
Victor Kleptsyn
М
21:49
Математические байки
Но если прямая проходит через точку P, то мы можем взять всю картину — сферу+касательную плоскость π в этой точке — и отразить её относительно той плоскости, что высекает прямую m.
Victor Kleptsyn
М
21:50
Математические байки
Так что если сохранится дуга большого круга на сфере — то сохранится и её проекция на плоскость π, и наоборот.
Victor Kleptsyn
М
21:50
Математические байки
А значит, угол прямой до проекции тогда и только тогда, когда после.
Victor Kleptsyn
М
21:51
Математические байки
И теперь у нас есть прекрасная возможность сослаться на теорему о высотах евклидовой геометрии!
Victor Kleptsyn
М
21:51
Математические байки
А именно — давайте возьмём в качестве точки P точку пересечения каких-нибдь двух из трёх высот, например, AH_A и BH_B.
Victor Kleptsyn
М
21:53
Математические байки
Тогда в проекции исходного треугольника мы получим евклидов треугольник, а проекции дуг большого круга AH_A и BH_B будут его высотами: они проходят через точку P, а значит, перпендикулярность им сохраняется.
Victor Kleptsyn
М
21:53
Математические байки
Но тогда и третья высота евклидова треугольника проходит через ту же точку!
Victor Kleptsyn
М
21:54
Математические байки
А значит, спроецировав её обратно на сферу (перпендикулярность сохраняется!), мы получим высоту CH_C, проходящую через ту же точку P.
Victor Kleptsyn
М
21:54
Математические байки
Всё, победа!
Victor Kleptsyn
М
21:54
Математические байки
И вот это рассуждение я знаю от Хованского.
Victor Kleptsyn
М
21:55
Математические байки
Точнее, и то, и другое мне рассказывали в [более сложном] варианте "для плоскости Лобачевского" — откуда вернуться на сферу совсем просто.
Victor Kleptsyn
М
21:59
Математические байки
Арнольдовское рассуждение в этом случае использовало тождество Якоби для матриц 2x2 — и его можно посмотреть в его статье в Мат. просвещении: http://mi.mathnet.ru/mp165
Victor Kleptsyn
М
22:02
Математические байки
А рассуждение Хованского — модель Клейна в диске вместо центральной проекции. А именно, в модели Клейна прямым плоскости Лобачевского соответствуют отрезки. И если из двух прямых хотя бы одна проходит через евклидов центр P диска-модели, то их перпендикулярность в плоскости Лобачевского равносильна перпендикулярности в евклидовом смысле.
Victor Kleptsyn
М
22:03
Математические байки
Но — я обещал одну оговорку. Дело в том, что в собственно плоскости Лобачевского высоты могут... не пересечься совсем.
Victor Kleptsyn
М
22:05
Математические байки
В смысле модели Клейна это несложно увидеть — достаточно взять треугольник, у которого одна из вершин это евклидов центр диска P (и тем самым две его евклидовых высоты это и его высоты в смысле плоскости Лобачевского), и при этом который достаточно "тупоугольный" и "большой", чтобы точка евклидова пересечения высот попала бы за диск-модель.
Victor Kleptsyn
М
22:16
Математические байки
В этом случае можно (во внутренних терминах геометрии Лобачевского) сказать, что у всех трёх высот есть общая перпендикулярная им прямая — или можно, следуя Арнольду, считать, что плоскость Лобачевского это часть плоскости со "знакоопределённой" метрикой, за которой есть релятивистский мир де Ситтера —
Victor Kleptsyn
М
22:16
Математические байки
Скриншот отсюда — https://math.ru/lib/files/pdf/mehmat/mm3.pdf
Victor Kleptsyn
М
22:30
Математические байки
(И мне кажется, там интересно посмотреть всё интервью; отдельно трогательны рисунки, сделанные рукой самого В.И.А.)
Victor Kleptsyn
М
22:31
Математические байки
Кстати — такая же картинка есть и в "Мат. понимании природы" В.И.А.,
https://www.mccme.ru/free-books/arnold/VIA-mpp.pdf
https://www.mccme.ru/free-books/arnold/VIA-mpp.pdf
Victor Kleptsyn
М
22:32
Математические байки
Ну и на этой исторической ноте, кажется, мне правильно на сегодня прекратить дозволенные речи.
Victor Kleptsyn
19 February 2020
М
08:48
Математические байки
Пару недель назад прошёл очередной « Математический праздник » — и подборка задач разных лет (https://olimpiada.ru/article/863 ) мне напомнила о задаче 2001 года С. Маркелова:
Victor Kleptsyn
М
08:48
Математические байки
« В книге рекордов Гиннесса написано, что наибольшее известное простое число равно 23021^{377} – 1. Не опечатка ли это? »
Victor Kleptsyn
М
08:50
Математические байки
Кстати, на самом Матпразднике из этой подборки сделали отдельный стенд, и мне кажется, это была исключительно удачная идея: все подходили и смотрели —
Victor Kleptsyn
М
09:02
Математические байки
(Да, а вот тут коллеги выложили PDF-файл постера)
Victor Kleptsyn
М
09:02
Математические байки
Н
Непрерывное математическое образование 19.02.2020 00:50:56
обновленный постер с задачами Математического праздника в подходящем для печати качестве
Victor Kleptsyn
М
09:03
Математические байки
Так вот, сегодняшняя байка посвящена простым числам Мерсенна: простым числам вида M(p):=2^p-1, где p простое.
(Я её уже рассказывал год назад, но в непубличном чате; заранее прошу прощения у тех, кто её от меня уже тогда слышал.)
(Я её уже рассказывал год назад, но в непубличном чате; заранее прошу прощения у тех, кто её от меня уже тогда слышал.)
Victor Kleptsyn
М
09:04
Математические байки
Чуть больше года назад, в декабре 2018-го, нашли очередное простое число Мерсенна, M(82 589 933), ставшее самым большим известным простым числом — что, разумеется, немедленно пробежало по новостям. А если посмотреть на список самых больших известных простых чисел (https://en.wikipedia.org/wiki/Largest_known_prime_number#The_twenty_largest_known_prime_numbers ), то там из первой десятки только одно не-Мерсенновское, да и остальные визуально очень на них похожи. И с 1952-го года только один раз на три года самое большой известное число было не-Мерсенновским: с 1989 по 1992 « царём горы » было 391581×2^{216193}-1.
Victor Kleptsyn
М
09:05
Математические байки
При этом Мерсенновских чисел очень мало (это же «почти степень двойки») — при том, что вообще-то простых довольно много: доля простых среди первых n чисел это 1/ln n, что, конечно, стремится к 0 — но довольно медленно. Скажем, из 100-значных чисел простым будет примерно каждое 230-е; собственно, ровно так работает поиск простых для RSA-криптографии: тыкаем в случайные большие числа, пока не наткнёмся на простое. И тысяча-другая попыток тут это много, но не смертельно.(А вот если бы простых от 1 до n было бы порядка sqrt{n}, всё было бы совсем по-другому…)
Victor Kleptsyn
М
09:08
Математические байки
Так почему же самые большие известные простые — Мерсенновские? Потому что « ищем под фонарём », то есть — потому что именно для них есть очень быстрый алгоритм проверки на простоту, тест Люка-Лемера. И с ним очень интересно разобраться.
Victor Kleptsyn
М
09:08
Математические байки
Его "замкнутая" формулировка "в готовом к исполнению" виде выглядит, как совершенно непонятный « чёрный ящик »: ясно, куда подключать провода, но как и почему он работает, загадка.
Victor Kleptsyn
М
09:09
Математические байки
А именно: строим последовательность вычетов s_n по модулю M, где M=2^p-1 — наш кандидат в простые Мерсенна, по следующему рекуррентному правилу:
- начинаем с s_1=4,
- каждое следующее s_{n+1}=s_n^2-2 (mod M).
Теорема. M простое тогда и только тогда, когда S_{p-1}=0.
- начинаем с s_1=4,
- каждое следующее s_{n+1}=s_n^2-2 (mod M).
Теорема. M простое тогда и только тогда, когда S_{p-1}=0.
Victor Kleptsyn
М
09:10
Математические байки
Victor Kleptsyn
М
09:10
Математические байки
Пример. Возьмём p=5. По модулю M=31 получаем последовательность
4, 14, 194=8 (31), 62=0 (31) — победа.
Чуть-чуть повторяясь — « Куда заливать бензин и как запускать, понятно. А почему же оно всё работает? »
4, 14, 194=8 (31), 62=0 (31) — победа.
Чуть-чуть повторяясь — « Куда заливать бензин и как запускать, понятно. А почему же оно всё работает? »
Victor Kleptsyn
М
09:16
Математические байки
Для начала — давайте мысленно поделим последовательность s_n на 2 (благо, что по нечётному модулю M это проблемы не создаёт; ну или можно сначала делить, она останется целой, а потом уже приводить по модулю).
Для новой последовательности t_n реккурентное соотношение это t_{n+1}=2 t_n^2-1.
И это уже начинает что-то напоминать: P(t)=2 t^2-1 это формула для косинуса двойного угла (она же многочлен Чебышева степени 2).
Для новой последовательности t_n реккурентное соотношение это t_{n+1}=2 t_n^2-1.
И это уже начинает что-то напоминать: P(t)=2 t^2-1 это формула для косинуса двойного угла (она же многочлен Чебышева степени 2).
Victor Kleptsyn
М
09:18
Математические байки
А косинус двойного угла, если перейти в комплексные числа и рассмотреть там z=cos a + i sin a, это просто возведение в квадрат. А череда из k возведений в квадрат это возведение в степень 2^k. И это уже начинает с числами Мерсенна (M=2^p-1) иметь что-то общее — ещё не формально, но на уровне "это явно кусочек от той же головоломки".
Victor Kleptsyn
М
09:19
Математические байки
Пытаясь сделать что-то чуть более формально, мы замечаем, что всё начинается с t_1=2, а косинус, равный двум, это немного странно. Но давайте всё равно посмотрим, чему бы равнялось соответствующее комплексное z?
Если z=e^{ia} = cos a + i sin a, то cos a= (z+1/z)/2.
Соответственно, уравнение (z+1/z)/2=2 даёт корни z=2+\sqrt{3} и z=2-\sqrt{3}.
Если z=e^{ia} = cos a + i sin a, то cos a= (z+1/z)/2.
Соответственно, уравнение (z+1/z)/2=2 даёт корни z=2+\sqrt{3} и z=2-\sqrt{3}.
Victor Kleptsyn
М
09:21
Математические байки
И кстати, сразу видно, что удобнее работать не с косинусом, а с удвоенным косинусом, так нет двойки в знаменателе.
Поэтому с этого момента мы вернёмся к исходной последовательности s_n.
Так вот — для уже вовсе не комплексного z=2+\sqrt{3} мы получаем z+1/z =4. И поэтому члены нашей исходной последовательности s_n до приведения по модулю M получаются как
s_n=(2+\sqrt{3})^{2^{n-1}} + (2-\sqrt{3})^{2^{n-1}}
Поэтому с этого момента мы вернёмся к исходной последовательности s_n.
Так вот — для уже вовсе не комплексного z=2+\sqrt{3} мы получаем z+1/z =4. И поэтому члены нашей исходной последовательности s_n до приведения по модулю M получаются как
s_n=(2+\sqrt{3})^{2^{n-1}} + (2-\sqrt{3})^{2^{n-1}}
Victor Kleptsyn
М
М
09:24
Математические байки
Осталось понять, при чём же тут всё-таки числа Мерсенна, как будет играть степень двойки, и что нам делать с корнем из 3 при работе с вычетами.
Victor Kleptsyn
М
11:17
Математические байки
На самом деле — ассоциация с комплексными числами тут очень по делу. Комплексные числа получаются из вещественных, если к ним добавить корень уравнения x^2+1=0, у которого в самом поле вещественных чисел корня нет.
Этот корень мы обозначаем через i; при этом в комплексных числах у этого уравнения есть два равноправных (с точки зрения вещественных чисел) корня, i и -i, и переводя один из них в другой, мы получаем автоморфизм комплексных чисел — комплексное сопряжение.
Этот корень мы обозначаем через i; при этом в комплексных числах у этого уравнения есть два равноправных (с точки зрения вещественных чисел) корня, i и -i, и переводя один из них в другой, мы получаем автоморфизм комплексных чисел — комплексное сопряжение.
Victor Kleptsyn
М
11:17
Математические байки
Точно так же вместо вещественных чисел можно взять, например, поле из 7 элементов — вычеты по модулю 7.
В нём у уравнения x^2+1=0 тоже нет корней (упражнение: проверьте это!). И добавив такой корень — и всё, что добавится из-за этого — мы получим поле из 7^2=49 элементов, элементы которого это комбинации вида a+bx (где x — наш корень). Классический вопрос « для каких простых p по модулю p есть корень из (-1) » имеет столь же классический ответ « для двойки и простых вида 4k+1 ».
В нём у уравнения x^2+1=0 тоже нет корней (упражнение: проверьте это!). И добавив такой корень — и всё, что добавится из-за этого — мы получим поле из 7^2=49 элементов, элементы которого это комбинации вида a+bx (где x — наш корень). Классический вопрос « для каких простых p по модулю p есть корень из (-1) » имеет столь же классический ответ « для двойки и простых вида 4k+1 ».
Victor Kleptsyn
М
11:18
Математические байки
Так вот — мы для нашей последовательности хотим рассмотреть числа, включающие в свою запись «корень из 3», и работать с ними «по модулю M». Вспомогательная лемма, которую мы сейчас принимаем на веру: для любого M=2^p-1, где простое p>2, из 3 по модулю M корень извлечь нельзя.
Victor Kleptsyn
М
11:18
Математические байки
Следствие. Если M простое, то мы имеем право рассмотреть не только поле вычетов по модулю M, но и поле из M^2 элементов, получающееся добавлением x=\sqrt{3}. В котором есть «сопряжение» — замена знака перед \sqrt{3}.
Victor Kleptsyn
М
11:19
Математические байки
Второе — важное само по себе — утверждение, это что мультипликативная группа конечного поля циклична. То есть что все ненулевые его элементы есть степень некоторого одного, поэтому операция «умножить» превращается ( если его знать) в операцию «сложить степени».
Victor Kleptsyn
М
11:20
Математические байки
А давайте посмотрим, из скольки элементов состоит эта мультипликативная группа для нашего нового поля — то есть по какому модулю будет сложение степеней?
Всех элементов в поле M^2, без нуля
M^2-1=(M-1)(M+1) = 2^p (2^p-2).
И у нас внезапно образовалась группа, порядок которой делится на очень большую степень двойки (на 2^{p+1}, если быть точным).
Всех элементов в поле M^2, без нуля
M^2-1=(M-1)(M+1) = 2^p (2^p-2).
И у нас внезапно образовалась группа, порядок которой делится на очень большую степень двойки (на 2^{p+1}, если быть точным).
Victor Kleptsyn
20 February 2020
М
14:32
Математические байки
Давайте закончим доказательство теста Люка-Лемера. Для начала посмотрим, какое у него условие «успешного окончания». Это s_{p-1}=0 — «вещественная (точнее, не содержащая \sqrt{3}) компонента» у числа z^{2^{p-2}} равна нулю.
Если бы речь шла о косинусе, это бы значило, что 2 cos a=0, и соответствующие комплексные числа были бы i и -i; а их квадрат равнялся бы (-1).
Собственно, s_{p-1}=0 равносильно тому, что s_{p}=-2, то есть z^{2^{p-1}}=-1.
Если бы речь шла о косинусе, это бы значило, что 2 cos a=0, и соответствующие комплексные числа были бы i и -i; а их квадрат равнялся бы (-1).
Собственно, s_{p-1}=0 равносильно тому, что s_{p}=-2, то есть z^{2^{p-1}}=-1.
Victor Kleptsyn
М
14:32
Математические байки
Не то, чтобы это было обязательно — но вот пример для p=5 (которое приводит к действительно простому M=31):
Victor Kleptsyn
М
14:33
Математические байки
Жирным тут выделены значения t_j — "вещественные части", половинки от последовательности s_j.
Victor Kleptsyn
М
14:34
Математические байки
Итак, от z=2+\sqrt{3} (соответствующего s_1=4 или t_1=2) мы за p-2=3 итерации дошли до s_{p-1}=t_{p-1}=0, а за ещё одну — до z^{2^{p-1}}=-1 (и, соответственно, s_p=-2, t_p=-1). Если бы мы ещё один раз возвели в квадрат — воткнулись бы в единицу, которая для возведения в квадрат неподвижная точка.
Victor Kleptsyn
М
14:34
Математические байки
Давайте посмотрим, почему мы этого не сделали — и почему всё было настолько « близко », что стоит M оказаться составным, и ничего не получится. И заодно выясним много интересного, что живёт «по соседству».
Victor Kleptsyn
М
14:35
Математические байки
Во-первых, если у нас есть поле из q элементов (где q нечётное), то есть очень симпатичная формула, позволяющая проверить, является ли его элемент квадратом (в этом поле!). А именно — малая теорема Ферма для простого q и теорема Лагранжа для q=M^k утверждают, что w^{q-1}=1 для всех элементов поля.
Victor Kleptsyn
М
М
М
14:37
Математические байки
Доказательство. Если w=r^2, то w^{(q-1)/2}=r^{q-1}=1.
Квадратов от ненулевых элементов поля ровно половина, поэтому все возможные корни уравнения w^{(q-1)/2}=1 (столько, какова его степень) мы уже посчитали. Но половинная степень, если её возвести в квадрат, должна дать w^{q-1}=1, а корни из 1 это только 1 и (-1). Значит, все не-квадраты дают (-1).
Квадратов от ненулевых элементов поля ровно половина, поэтому все возможные корни уравнения w^{(q-1)/2}=1 (столько, какова его степень) мы уже посчитали. Но половинная степень, если её возвести в квадрат, должна дать w^{q-1}=1, а корни из 1 это только 1 и (-1). Значит, все не-квадраты дают (-1).
Victor Kleptsyn
М
14:38
Математические байки
И уже сразу видна похожесть на нашу ситуацию — мы возводим в степень (правда, не совсем в ту), и получаем (-1).
Victor Kleptsyn
М
14:39
Математические байки
Во-вторых, как и в комплексных числах, в таком «квадратичном расширении» тоже есть понятие нормы — произведение
||w||=w*conj(w),
где conj — сопряжение, изменяющее знак у \sqrt{3}.
Это скорее аналог квадрата длины комплексного числа, но в теории Галуа правильно использовать именно такое определение. И как легко видеть, наше z=2+\sqrt{3} имеет единичную норму:
(2+\sqrt{3})(2-\sqrt{3})=4-3=1.
||w||=w*conj(w),
где conj — сопряжение, изменяющее знак у \sqrt{3}.
Это скорее аналог квадрата длины комплексного числа, но в теории Галуа правильно использовать именно такое определение. И как легко видеть, наше z=2+\sqrt{3} имеет единичную норму:
(2+\sqrt{3})(2-\sqrt{3})=4-3=1.
Victor Kleptsyn
М
14:39
Математические байки
(А в общем случае — см.
https://kconrad.math.uconn.edu/blurbs/galoistheory/tracenorm.pdf или https://en.wikipedia.org/wiki/Field_trace )
https://kconrad.math.uconn.edu/blurbs/galoistheory/tracenorm.pdf или https://en.wikipedia.org/wiki/Field_trace )
Victor Kleptsyn
М
14:41
Математические байки
В третьих, если у нас есть поле из M^k элементов (характеристики M), то у него есть автоморфизм
a->a^M.
Потому что, раскрыв по биному, получаем (a+b)^M=a^M+b^M (все остальные биномиальные коэффициенты делятся на M). Этот автоморфизм «именной» — он называется автоморфизмом Фробениуса.
a->a^M.
Потому что, раскрыв по биному, получаем (a+b)^M=a^M+b^M (все остальные биномиальные коэффициенты делятся на M). Этот автоморфизм «именной» — он называется автоморфизмом Фробениуса.
Victor Kleptsyn
М
14:42
Математические байки
Более того, он порождает группу автоморфизмов поля — которая оказывается циклической, и состоит из k элементов: после k его применений мы получаем возведение в степень M^k — которая есть тождественное отображение (как мы уже видели выше — в виде равенства w^{q-1}=1).
Victor Kleptsyn
М
14:43
Математические байки
И вообще автоморфизм Фробениуса в теории Галуа это один из фундаментальных кирпичиков — такой же, как понятие предела или интеграла в анализе.
Victor Kleptsyn
М
14:45
Математические байки
Но в нашем случае мы уже знаем единственный нетривиальный автоморфизм поля из M^2 элементов: это изменение знака у корня из 3. Значит, conj(w)=w^M, откуда
||w||=w*conj(w)=w^{M+1}.
||w||=w*conj(w)=w^{M+1}.
Victor Kleptsyn
М
14:46
Математические байки
In reply to this message
И паззл начинает склеиваться — M+1=2^p. А у нас было возведение в половинную степень: нам нужно проверить, что
z^{2^{p-1}}=-1.
z^{2^{p-1}}=-1.
Victor Kleptsyn
М
14:47
Математические байки
Так вот: давайте посмотрим не на всю группу ненулевых элементов поля, а на её подгруппу, состоящую из элементов нормы 1 — из корней уравнения w^{M+1}=1.
Victor Kleptsyn
М
14:50
Математические байки
Эта группа состоит, как несложно видеть, из M+1 элемента, и это циклическая группа. Например, как подгруппа циклической, хотя приятнее тут сослаться на вообще общее утверждение: конечная подгруппа мультипликативной группы любого поля циклична.
Victor Kleptsyn
М
14:51
Математические байки
(Его доказательство — отдельное красивое упражнение, но речь сейчас не об этом :) ).
Victor Kleptsyn
М
14:53
Математические байки
In reply to this message
Так вот — у нас есть подгруппа элементов нормы 1, состоящая из N=M+1 элемента. Повторяя рассуждения выше, несложно увидеть, что её элемент w является квадратом внутри этой подгруппы тогда и только тогда, когда половинная степень w^{N/2} равна 1 — а иначе получаем (-1).
Victor Kleptsyn
М
14:54
Математические байки
Поэтому всё, что нам нужно проверить, чтобы знать, что мы действительно получаем z^{2^{p-1}}=-1 (и поэтому s_{p}=-2, s_{p-1}=0) — это что z=2+\sqrt{3} не является квадратом элемента нормы 1!
Victor Kleptsyn
М
15:00
Математические байки
А этому более-менее соответствует то, что "шаг назад" от s_1 мы сделать не сможем: не будет такого s_0, для которого s_0^2 - 2 = 4 = s_1 (mod M).
И не будет его потому, что это означало бы извлечение корня из 6 по модулю M. Но из 3 корня по модулю M нет (с этой декларации мы и начали рассказ, и это следует из квадратичного закон взаимности), а из 2, напротив, всегда есть: ведь 2^{p+1}=2 mod M, а значит, корнем будет 2^{(p+1)/2}. Из 2 корень есть, из 3 нет — значит, нет и из их произведения 6=2*3.
И не будет его потому, что это означало бы извлечение корня из 6 по модулю M. Но из 3 корня по модулю M нет (с этой декларации мы и начали рассказ, и это следует из квадратичного закон взаимности), а из 2, напротив, всегда есть: ведь 2^{p+1}=2 mod M, а значит, корнем будет 2^{(p+1)/2}. Из 2 корень есть, из 3 нет — значит, нет и из их произведения 6=2*3.
Victor Kleptsyn
М
15:07
Математические байки
In reply to this message
Если говорить совсем аккуратно — то если
w=(t+r \sqrt{3})^2 = (2+\sqrt{3})
и w нормы 1, то t^2-3r^2=1, а при раскрытии скобок по «вещественной» части получается
t^2+3r^2 = 2t^2- (t^2-3r^2)=2t^2-1,
и уравнение
2 t^2-1=2
это то же самое уравнение
s^2-2=4,
переписанное в терминах t=s/2.
w=(t+r \sqrt{3})^2 = (2+\sqrt{3})
и w нормы 1, то t^2-3r^2=1, а при раскрытии скобок по «вещественной» части получается
t^2+3r^2 = 2t^2- (t^2-3r^2)=2t^2-1,
и уравнение
2 t^2-1=2
это то же самое уравнение
s^2-2=4,
переписанное в терминах t=s/2.
Victor Kleptsyn
М
15:10
Математические байки
Вот. Давайте я подытожу — мы пока сделали проход в одну сторону, что если M=2^p-1 простое, то s_{p-1}=0. Но мы возводили в столь большую степень двойки — что в объяснение "ну, если M разложится на множители, то мы по модулю хотя бы одного из сомножителей в (-1) не попадём" кажется как минимум правдоподобным.
Victor Kleptsyn
М
15:10
Математические байки
И вот так этот "чёрный ящик" теста и работает!
Victor Kleptsyn
М
15:12
Математические байки
В качестве постскриптума — совсем другой рассказ о том же:
А.Н.Рудаков, Числа Фибоначчи и простота числа 2^{127}-1 — см. https://www.mccme.ru/free-books/matpros5.html
А.Н.Рудаков, Числа Фибоначчи и простота числа 2^{127}-1 — см. https://www.mccme.ru/free-books/matpros5.html
Victor Kleptsyn
М
15:21
Математические байки
===
И — пара слов совсем о другом. Вот в теории бильярдов есть довольно много проблем, которые легко сформулировать, но которые при этом оказываются безумно сложными.
Один такой вопрос — это существование периодической траектории в бильярде в любом треугольнике.
И — пара слов совсем о другом. Вот в теории бильярдов есть довольно много проблем, которые легко сформулировать, но которые при этом оказываются безумно сложными.
Один такой вопрос — это существование периодической траектории в бильярде в любом треугольнике.
Victor Kleptsyn
М
15:24
Математические байки
(Чуть более формально — материальная точка движется внутри треугольника, отражаясь по закону "угол падения равен углу отражения"; траектории, в какой-то момент попадающие в вершины, мы не рассматриваем.)
Victor Kleptsyn
М
15:29
Математические байки
Для остроугольного треугольника траекторию можно предъявить явно — простой и красивый геометрический факт состоит в том, что можно взять траекторию через три основания высот.
Victor Kleptsyn
М
15:30
Математические байки
(Фото с лестницы МЦНМО — спасибо Г. Мерзону!)
Victor Kleptsyn
М
15:35
Математические байки
А это фото с сегодняшней лекции А. Глуцюка (вводный рассказ о бильярдах) — и на правой половине левой доски видно как раз доказательство (школьное :) )
Victor Kleptsyn
М
15:36
Математические байки
Так вот — в прямоугольном треугольнике это всё ещё упражнение. А вот в тупоугольных — большой открытый вопрос. (Нет, в любом конкретном, конечно, можно найти; и даже знают, что если все углы соизмеримы с π, то есть; но общий случай открыт.)
Victor Kleptsyn
М
15:43
Математические байки
Кстати, про прямоугольный треугольник — есть прекрасная задача про столкновения масс на прямой, превращающаяся в задачу о бильярде и в итоге (spoilers!) приводящая к появлению π в ответе.
Вот тут есть ролик 3blue1brown об этом —
https://www.youtube.com/watch?v=HEfHFsfGXjs —
а я узнал об этом, если не ошибаюсь, в ЛШСМ-2004 от самого Гальперина, статью которого "Playing pool with π (the number π from a billiard point of view)" (https://www.maths.tcd.ie/~lebed/Galperin.%20Playing%20pool%20with%20pi.pdf ) 3blue1brown цитирует:
Вот тут есть ролик 3blue1brown об этом —
https://www.youtube.com/watch?v=HEfHFsfGXjs —
а я узнал об этом, если не ошибаюсь, в ЛШСМ-2004 от самого Гальперина, статью которого "Playing pool with π (the number π from a billiard point of view)" (https://www.maths.tcd.ie/~lebed/Galperin.%20Playing%20pool%20with%20pi.pdf ) 3blue1brown цитирует:
Victor Kleptsyn
М
15:46
Математические байки
А ещё одна открытая проблема, которую сегодня Глуцюк упоминал, это гипотеза Иврия.
Вот если мы поставим точку прямо в центр круглого бильярда, то в какую бы сторону мы её не направили, траектория будет периодична. Или — если мы возьмём квадратный бильярд и запустим из любой точки траекторию под углом с рациональным коэффициентом наклона, опять-таки, траектория обязательно будет периодической.
Вот если мы поставим точку прямо в центр круглого бильярда, то в какую бы сторону мы её не направили, траектория будет периодична. Или — если мы возьмём квадратный бильярд и запустим из любой точки траекторию под углом с рациональным коэффициентом наклона, опять-таки, траектория обязательно будет периодической.
Victor Kleptsyn
М
15:47
Математические байки
А бывают ли такие "фокусирующие" бильярды (уже просто с гладкой границей, но вовсе не с многоугольной), у которых есть _открытое_ множество периодических траекторий? То есть если поставить шарик примерно в правильное место и ударить под примерно правильным углом — то траектория обязательно замкнётся?
Victor Kleptsyn
М
15:48
Математические байки
Гипотеза (В. Иврий, 1980). Нет, таких бильярдов нет.
Victor Kleptsyn
М
15:54
Математические байки
У него эта гипотеза возникла в связи с собственными значениями оператора Лапласа — в предположении, что таких открытых областей траекторий нет, он получил следующий член их асимптотики.
Victor Kleptsyn
М
15:54
Математические байки
Так что он, недолго думая, пришёл на семинар Синая и спросил. И ему сказали, что ну конечно же, это правда, приходите через неделю на следующее заседание, всё докажем.
Victor Kleptsyn
М
15:55
Математические байки
Он пришёл. Задача оказалась чуть более сложной — но ещё через неделю точно приходите, всё будет. Потом эта неделя стала месяцем...
Victor Kleptsyn
М
15:55
Математические байки
...и вопрос открыт до сих пор. :)
Victor Kleptsyn
М
16:00
Математические байки
Вот статья Иврия 1980 года — http://mi.mathnet.ru/faa1796 — а теорему о том, что таких четырёхугольных траекторий не бывает, доказали Глуцюк и Кудряшов в 2012 году:
http://www.aimsciences.org/article/doi/10.3934/jmd.2012.6.287
http://www.aimsciences.org/article/doi/10.3934/jmd.2012.6.287
Victor Kleptsyn
М
16:00
Математические байки
(Про треугольные знали раньше, пятиугольные и выше — вопрос всё ещё открыт...)
Victor Kleptsyn
М
16:02
Математические байки
Ну и на этой истории я хочу на сегодня прекратить дозволенные речи.
Victor Kleptsyn
25 February 2020
М
15:33
Математические байки
Сегодняшняя байка будет о применении эллиптических кривых в криптографии, как для защиты (что более известно), так и для «нападения»-факторизации (что,
почему-то, известно заметно меньше, хотя алгоритм именной, называется алгоритмом Ленстры).
(На всякий случай: рассказ по открытым источникам :) )
почему-то, известно заметно меньше, хотя алгоритм именной, называется алгоритмом Ленстры).
(На всякий случай: рассказ по открытым источникам :) )
Victor Kleptsyn
М
15:33
Математические байки
Но сначала — старая красивая задача: в одной далёкой стране почта доставляет любую посылку по адресу, но всё, что из неё можно изъять без применения ломика
с автогеном, исчезает. В этой стране живут два человека, А и Б, и А хочет переслать Б бриллиант. У каждого из них есть свой навесной замок (с ключом),а у А ещё и железный ящик с петлями, на который такой замок можно навесить — если ящик закрыть на замок, внутрь залезть никто не сможет. Но без ключа тогда открыть его нельзя.
Вопрос: как А переслать Б бриллиант?
с автогеном, исчезает. В этой стране живут два человека, А и Б, и А хочет переслать Б бриллиант. У каждого из них есть свой навесной замок (с ключом),а у А ещё и железный ящик с петлями, на который такой замок можно навесить — если ящик закрыть на замок, внутрь залезть никто не сможет. Но без ключа тогда открыть его нельзя.
Вопрос: как А переслать Б бриллиант?
Victor Kleptsyn
М
15:34
Математические байки
Скажем, А может отправить Б ящик с бриллиантом, закрытый на замок. И Б его получит. Но без ключа А получатель не сможет этот замок открыть — а задача пересылки ключа ничем не отличается от пересылки бриллианта.
Victor Kleptsyn
М
15:34
Математические байки
Если вдруг вы эту задачу не решали — она очень классная, и над ней стоит подумать. (Но в следующих сообщениях будет решение и его обсуждение, так что тогда пока не читайте дальше, или подождите немного и промотайте сильно вниз!)
Victor Kleptsyn
М
15:35
Математические байки
Так вот — первым делом А приходится прислать Б ящик с бриллиантом, закрытый на замок А. Но после этого Б — от обиды, что не может открыть — навешивает на него ещё и свой замок!
И посылает обратно А ящик, закрытый уже на два замка, и А, и Б. Получив его, А со словами « это моё, это я заберу » снимает свой замок — остаётся ящик с бриллиантом, закрытый на замок Б. Он его пересылает Б, тот снимает свой замок и забирает бриллиант.
И посылает обратно А ящик, закрытый уже на два замка, и А, и Б. Получив его, А со словами « это моё, это я заберу » снимает свой замок — остаётся ящик с бриллиантом, закрытый на замок Б. Он его пересылает Б, тот снимает свой замок и забирает бриллиант.
Victor Kleptsyn
М
15:36
Математические байки
Давайте уберём метафору и посмотрим, что же нужно, чтобы эта схема функционировала.
Замок и ключ, это, конечно, шифры, а бриллиант — пересылаемое сообщение. И тут нужны две важные вещи:
*) шифры должны коммутировать: мы взяли сообщение, сначала зашифровали его шифром А, а потом результат шифром Б; после этого « снимаем замок А » — применяем расшифровывающее отображение — и хотим получить сообщение, зашифрованное чисто шифром Б.
*) знание для одного из шифров какой-то пары из исходного и зашифрованного сообщения не должно помогать атакующему: по открытому каналу передаются как «сообщение» А(бриллианта), так и его «результат Б-шифровки» Б(А(бриллианта)).
Замок и ключ, это, конечно, шифры, а бриллиант — пересылаемое сообщение. И тут нужны две важные вещи:
*) шифры должны коммутировать: мы взяли сообщение, сначала зашифровали его шифром А, а потом результат шифром Б; после этого « снимаем замок А » — применяем расшифровывающее отображение — и хотим получить сообщение, зашифрованное чисто шифром Б.
*) знание для одного из шифров какой-то пары из исходного и зашифрованного сообщения не должно помогать атакующему: по открытому каналу передаются как «сообщение» А(бриллианта), так и его «результат Б-шифровки» Б(А(бриллианта)).
Victor Kleptsyn
М
15:36
Математические байки
Так, есть простой шифр « прибавление секретного ключа K » [например, с приведением по публично объявленному модулю].
Он удовлетворяет первому условию — прибавления ключей K_A и K_B коммутируют — но не удовлетворяет второму: по сообщению и его зашифрованному образу атакующий мгновенно восстанавливает секретный ключ, и дальше расшифровывает все остальные сообщения.
Он удовлетворяет первому условию — прибавления ключей K_A и K_B коммутируют — но не удовлетворяет второму: по сообщению и его зашифрованному образу атакующий мгновенно восстанавливает секретный ключ, и дальше расшифровывает все остальные сообщения.
Victor Kleptsyn
М
15:37
Математические байки
Зато можно такую схему реализовать с возведением в степень вместо сложения (и получается не алгоритм RSA, хоть и визуально похожий). А именно:
*) Публично объявлено большое [как положено, сотня-тысяча знаков) простое число P.
*) У каждого из А и Б есть свои секретные ключи — [большие] числа a и b, взаимно простые с P-1.
Раз a и P-1 взаимно-простые, то из алгоритма Евклида А знает такое R, что aR сравнимо с 1 по модулю P-1.
И тогда по модулю P операции возведения в степень a и в степень R взаимно-обратны: для любого
сообщения M выполнено (M^a)^R=M^(aR) = M, поскольку M^(P-1)=1, а aR=1 mod (P-1).
Поэтому возведение в степень a можно счесть « А-шифровкой », а в степень R — « А-расшифровкой »
Точно так же, Б знает такое S, что bS=1 mod (P-1), и возведения в степень b и в степень S обратны
друг другу, и мы возьмём их как Б-шифрование и Б-расшифровку.
*) Публично объявлено большое [как положено, сотня-тысяча знаков) простое число P.
*) У каждого из А и Б есть свои секретные ключи — [большие] числа a и b, взаимно простые с P-1.
Раз a и P-1 взаимно-простые, то из алгоритма Евклида А знает такое R, что aR сравнимо с 1 по модулю P-1.
И тогда по модулю P операции возведения в степень a и в степень R взаимно-обратны: для любого
сообщения M выполнено (M^a)^R=M^(aR) = M, поскольку M^(P-1)=1, а aR=1 mod (P-1).
Поэтому возведение в степень a можно счесть « А-шифровкой », а в степень R — « А-расшифровкой »
Точно так же, Б знает такое S, что bS=1 mod (P-1), и возведения в степень b и в степень S обратны
друг другу, и мы возьмём их как Б-шифрование и Б-расшифровку.
Victor Kleptsyn
М
15:38
Математические байки
Ну и, чтобы передать сообщение M от A к Б, им достаточно переслать друг другу сообщения (каждый раз приводя результат по модулю P, я этого каждый раз писать не буду):
1) (А вычисляет и отправляет) M^a
2) (Б добавляет свой шифр и пересылает обратно) (M^a)^b=M^(ab)
3) (А снимает свой шифр и пересылает опять Б) (M^(ab))^R = M^(abR)= M^b
4) (Б снимает свой шифр) (M^b)^S=M^(bS)=M.
Ура!
1) (А вычисляет и отправляет) M^a
2) (Б добавляет свой шифр и пересылает обратно) (M^a)^b=M^(ab)
3) (А снимает свой шифр и пересылает опять Б) (M^(ab))^R = M^(abR)= M^b
4) (Б снимает свой шифр) (M^b)^S=M^(bS)=M.
Ура!
Victor Kleptsyn
М
15:39
Математические байки
И видно, что формально-математически знание (M^a) и (M^a)^b позволяет восстановить b — но это задача « дискретного логарифмирования ». Соответственно, нужно, чтобы она была сложной (ну и, как совсем не специалист, я не полезу в вопросы того, когда она считается сложной, а когда нет).
См.: https://en.wikipedia.org/wiki/Three-pass_protocol
+ https://ru.wikipedia.org/wiki/%D0%9A%D1%80%D0%B8%D0%BF%D1%82%D0%BE%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D0%9C%D1%8D%D1%81%D1%81%D0%B8_%E2%80%94_%D0%9E%D0%BC%D1%83%D1%80%D1%8B
См.: https://en.wikipedia.org/wiki/Three-pass_protocol
+ https://ru.wikipedia.org/wiki/%D0%9A%D1%80%D0%B8%D0%BF%D1%82%D0%BE%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D0%9C%D1%8D%D1%81%D1%81%D0%B8_%E2%80%94_%D0%9E%D0%BC%D1%83%D1%80%D1%8B
Victor Kleptsyn
М
15:39
Математические байки
Буквально с этой задачей мы закончили — но та же идея коммутирующих шифров используется ещё одним способом, и именно тут применяют эллиптические кривые.
А именно — много что можно сделать, если у двух сторон есть общий секретный ключ. Только вот как сделать так, чтобы он оказался у обоих сторон сразу?
А именно — много что можно сделать, если у двух сторон есть общий секретный ключ. Только вот как сделать так, чтобы он оказался у обоих сторон сразу?
Victor Kleptsyn
М
15:41
Математические байки
Например: пусть две стороны заранее договорились о длинной совершенно случайной последовательности
нулей и единиц. Первый побитово прибавляет его к своему сообщению, пересылает результат, а второй такой же побитовой суммой восстанавливает исходное сообщение.
Это называется «шифр Вернама» ( https://ru.wikipedia.org/wiki/шифр_Вернама ), и при условии секретности (и случайности, и однократного использования) ключей он абсолютно надёжен —
любое кодированное сообщение может быть шифром любого исходного, если монетка выпадала нужной последовательностью. И с точки зрения перехватывающего, все возможные исходные сообщения равновероятны.
Но недостаток его состоит в том, что используемый секретный ключ (которым стороны обмениваются до сеанса связи) по длине совпадает с сообщением. То есть шифроблокноты нужно завозить как минимум чемоданами.
нулей и единиц. Первый побитово прибавляет его к своему сообщению, пересылает результат, а второй такой же побитовой суммой восстанавливает исходное сообщение.
Это называется «шифр Вернама» ( https://ru.wikipedia.org/wiki/шифр_Вернама ), и при условии секретности (и случайности, и однократного использования) ключей он абсолютно надёжен —
любое кодированное сообщение может быть шифром любого исходного, если монетка выпадала нужной последовательностью. И с точки зрения перехватывающего, все возможные исходные сообщения равновероятны.
Но недостаток его состоит в том, что используемый секретный ключ (которым стороны обмениваются до сеанса связи) по длине совпадает с сообщением. То есть шифроблокноты нужно завозить как минимум чемоданами.
Victor Kleptsyn
М
15:41
Математические байки
В качестве отступления в сторону: когда в 1940-ых в советской шифрованной переписке произошло повторное использование кодовых страниц (делающее атаку на шифр возможной) — американцы смогли некоторые сообщения расшифровать ( https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%BE%D0%B5%D0%BA%D1%82_%C2%AB%D0%92%D0%B5%D0%BD%D0%BE%D0%BD%D0%B0%C2%BB ).
И я тут процитирую из той же Википедии прекрасную формулировку:
«При этом складывалась парадоксальная ситуация: величайший секрет разведки США — чтение советских депеш, из которых узнали, что советская разведка знала величайший секрет британской разведки, состоявший в том, что они читали немецкие депеши.»
И я тут процитирую из той же Википедии прекрасную формулировку:
«При этом складывалась парадоксальная ситуация: величайший секрет разведки США — чтение советских депеш, из которых узнали, что советская разведка знала величайший секрет британской разведки, состоявший в том, что они читали немецкие депеши.»
Victor Kleptsyn
М
М
15:44
Математические байки
Но, конечно, шифром Вернама всё не исчерпывается — шифры, где один и тот же ключ используется для шифровки и для дешифровки, называются симметричными (см. https://en.wikipedia.org/wiki/Symmetric-key_algorithm ) — и их много. Главный вопрос — как получить общий секретный ключ.
Victor Kleptsyn
М
15:45
Математические байки
И позволяющий сделать это алгоритм — протокол Диффи-Хеллмана: https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%BE%D1%82%D0%BE%D0%BA%D0%BE%D0%BB_%D0%94%D0%B8%D1%84%D1%84%D0%B8_%E2%80%94_%D0%A5%D0%B5%D0%BB%D0%BB%D0%BC%D0%B0%D0%BD%D0%B0 ; в англовики на эту тему есть прекрасная картинка из той же Википедии:
Victor Kleptsyn
М
15:46
Математические байки
То есть — у нас есть некоторая общеизвестная «начальная точка» P, после чего стороны применяют к ней каждая свой шифр, пересылая друг другу результаты A(P) и B(P), и применяют к полученному от собеседника свой шифр — получая A(B(P)) и B(A(P)).
Если шифры коммутировали — то вот у них и получился общий секретный ключ. Вот только где добыть коммутирующие шифры?
Если шифры коммутировали — то вот у них и получился общий секретный ключ. Вот только где добыть коммутирующие шифры?
Victor Kleptsyn
М
15:47
Математические байки
Один пример — возведение в секретную степень по большому (известному) простому модулю — мы уже выше видели. А второй как раз доставляют эллиптические кривые — и давайте я наконец скажу, что это такое.
Victor Kleptsyn
М
15:47
Математические байки
Пусть на плоскости нарисована кривая, задаваемая уравнением третьей степени — F(x,y)=0 — и пусть она гладкая: без особых точек, как у « клюва » y^2=x^3, или самопересечения, как у
y^2=x^2(x+1).
Будем называть такую кривую эллиптической.
y^2=x^2(x+1).
Будем называть такую кривую эллиптической.
Victor Kleptsyn
М
15:49
Математические байки
Если быть более точным, то правильно эллиптическую кривую рассматривать не на обычной плоскости, а на проективной, добавляя к ней «точки на бесконечности».
Можно показать, что проективными преобразованиями такую кривую можно привести к более простому виду:
y^2=P(x),
где P — многочлен степени 3.
В этом виде единственной точкой на бесконечности будет точка на « вертикальной бесконечности » (в направлении (0,1)), к которой эта кривая стремится; кстати — это точка перегиба: касание кривой с бесконечно удалённой прямой третьего порядка.
Можно показать, что проективными преобразованиями такую кривую можно привести к более простому виду:
y^2=P(x),
где P — многочлен степени 3.
В этом виде единственной точкой на бесконечности будет точка на « вертикальной бесконечности » (в направлении (0,1)), к которой эта кривая стремится; кстати — это точка перегиба: касание кривой с бесконечно удалённой прямой третьего порядка.
Victor Kleptsyn
М
15:50
Математические байки
Так вот, оказывается, точки на эллиптической кривой тоже можно складывать!
Об этом можно почитать в брошюре Цфасмана и Острика (которую я очень люблю) —
https://www.mccme.ru/mmmf-lectures/books/#book-8 — но « парой штрихов » я это всё расскажу.
Об этом можно почитать в брошюре Цфасмана и Острика (которую я очень люблю) —
https://www.mccme.ru/mmmf-lectures/books/#book-8 — но « парой штрихов » я это всё расскажу.
Victor Kleptsyn
М
16:38
Математические байки
Итак: пусть у нас задана какая-то эллиптическая кривая, и заданы две точки на ней. Проведём через них прямую. Ограничение уравнение кривой на неё — это уравнение (в типичном случае) третьей степени, у которого уже есть два корня. Значит, будет и третий —
третья точка пересечения. Так вот, мы определим сложение точек на эллиптической кривой исходя из вот такого правила: сумма трёх точек, лежащих на одной прямой, равна нулю.
Но что такое ноль? Это, конечно, тоже одна из точек кривой, и в этом качестве мы выберем и зафиксируем какую-нибудь точку перегиба O.
третья точка пересечения. Так вот, мы определим сложение точек на эллиптической кривой исходя из вот такого правила: сумма трёх точек, лежащих на одной прямой, равна нулю.
Но что такое ноль? Это, конечно, тоже одна из точек кривой, и в этом качестве мы выберем и зафиксируем какую-нибудь точку перегиба O.
Victor Kleptsyn
М
16:40
Математические байки
Теперь понятно, как найти сумму P+Q точек P и Q на кривой — нужно провести прямую PQ, найти третью точку пересечения: (-P-Q). Теперь проведём прямую через (-P-Q) и O — и найдём искомую сумму P+Q.
Очевидно, что такое сложение коммутативно. А вот будет ли оно ассоциативно, правда ли, что (P+Q)+R=P+(Q+R)?
Очевидно, что такое сложение коммутативно. А вот будет ли оно ассоциативно, правда ли, что (P+Q)+R=P+(Q+R)?
Victor Kleptsyn
М
16:41
Математические байки
Оказывается, что будет — и при этом образуется красивая конфигурация из 9 точек, через которых проходят три кривых, задаваемых уравнением 3 степени: это произведение трёх « вертикальных » прямых, трёх « горизонтальных », и собственно наша эллиптическая кривая.
Victor Kleptsyn
М
16:42
Математические байки
(картинка из Цфасмана-Острика)
Victor Kleptsyn
М
16:43
Математические байки
А доказательство ассоциативности основано на таком факте:
Пусть есть восемь точек достаточно общего положения, и мы возьмём две проходящие через них кривые третьего порядка,
F_1(x,y)=0 и F_2(x,y)=0.
Они пересекаются в девяти ( =3*3, « теорема Безу ») точках, восьми наших, плюс ещё одна девятая. Так вот, тогда любая другая кривая третьего порядка
F(x,y)=0,
проходящая через исходные восемь точек, проходит и через девятую.
И происходит это по очень простой причине: уравнения тех кривых, которые проходят через эти 8 точек, это линейные комбинации F_1 и F_2. Которые, конечно, все обращаются в ноль в общих корнях F_1 и F_2, включая девятую точку.
Пусть есть восемь точек достаточно общего положения, и мы возьмём две проходящие через них кривые третьего порядка,
F_1(x,y)=0 и F_2(x,y)=0.
Они пересекаются в девяти ( =3*3, « теорема Безу ») точках, восьми наших, плюс ещё одна девятая. Так вот, тогда любая другая кривая третьего порядка
F(x,y)=0,
проходящая через исходные восемь точек, проходит и через девятую.
И происходит это по очень простой причине: уравнения тех кривых, которые проходят через эти 8 точек, это линейные комбинации F_1 и F_2. Которые, конечно, все обращаются в ноль в общих корнях F_1 и F_2, включая девятую точку.
Victor Kleptsyn
М
16:53
Математические байки
А вот эта картинка из статьи Н. Васильева в Кванте —
http://kvant.mccme.ru/1987/08/geksagrammy_paskalya_i_kubiche.htm
http://kvant.mccme.ru/1987/08/geksagrammy_paskalya_i_kubiche.htm
Victor Kleptsyn
М
17:01
Математические байки
In reply to this message
Эта статья называется "Гексаграммы Паскаля и кубические кривые" — потому что из этой же "теоремы о 9 точках" следует теорема Паскаля: три точки пересечения пар прямых, продолжающих противоположные стороны вписанного шестиугольника, лежат на одной прямой.
Что, собственно, правда не только для шестиугольника, вписанного в окружность, но и в любую другую конику [=кривую второго порядка].
Что, собственно, правда не только для шестиугольника, вписанного в окружность, но и в любую другую конику [=кривую второго порядка].
Victor Kleptsyn
М
17:08
Математические байки
И получается теорема Паскаля очень просто: девять точек это шесть вершин и три точки пересечения пар противоположных сторон, а три кривых третьего порядка это (совсем вырожденные) произведения уравнений сторон
l_1 l_3 l_5 =0 и l_2 l_4 l_6 =0
и чуть менее вырожденная
S*L=0,
где S — уравнение коники (на которой лежат 6 вершин), а L=0 — уравнение прямой, проходящей через две из трёх точек пересечения (и потому по теореме о девяти точках проходящей и через третью — что и доказывает теорему Паскаля).
l_1 l_3 l_5 =0 и l_2 l_4 l_6 =0
и чуть менее вырожденная
S*L=0,
где S — уравнение коники (на которой лежат 6 вершин), а L=0 — уравнение прямой, проходящей через две из трёх точек пересечения (и потому по теореме о девяти точках проходящей и через третью — что и доказывает теорему Паскаля).
Victor Kleptsyn
М
17:09
Математические байки
(Картинка из всё той же статьи Н. Васильева)
Victor Kleptsyn
М
17:15
Математические байки
Итак, точки на эллиптической кривой можно складывать. Причём — и это важно — эта операция рациональная: если у нас есть координаты двух складываемых точек (и уравнение самой кривой), то координаты суммы через них выражаются как рациональные функции, безо всяких там корней. Потому что нахождение третьего корня кубического уравнения при известных первых двух делается через теорему Виета про коэффициент при x^2, и там нужно только складывать/вычитать/делить, но не извлекать корни.
Victor Kleptsyn
М
17:16
Математические байки
(Кстати, удвоение точки тоже оказывается "рациональной" операцией — единственное, что нужно сказать, это что прямая PQ в этом случае заменяется на касательную к кривой.)
Victor Kleptsyn
М
17:18
Математические байки
А раз все операции рациональные — значит, всё то же самое можно делать и над конечными полями. (Давайте на всякий случай вынесем за скобки поля характеристик 2 и 3 — чтобы не контролировать, не могли ли двойки и тройки где-нибудь пробраться в знаменатели наших выражений)...
Victor Kleptsyn
26 February 2020
М
15:15
Математические байки
(Продолжая вчерашнее:)
Ну и теперь понятно, как через эллиптические кривые устроить протокол Диффи-Хеллмана. Пусть у нас публично объявлена эллиптическая кривая над большим конечным полем и точка P на ней. Для создания общего секретного ключа А и Б выбирают по большому числу a и b и вычисляют aP и bP соответственно. После этого А посылает Б точку aP (открыто), а Б посылает А точку bP (тоже открыто). И А вычисляет a(bP), а Б – b(aP), и вот они получили общий секретный ключ abP. Ура!
Ну и теперь понятно, как через эллиптические кривые устроить протокол Диффи-Хеллмана. Пусть у нас публично объявлена эллиптическая кривая над большим конечным полем и точка P на ней. Для создания общего секретного ключа А и Б выбирают по большому числу a и b и вычисляют aP и bP соответственно. После этого А посылает Б точку aP (открыто), а Б посылает А точку bP (тоже открыто). И А вычисляет a(bP), а Б – b(aP), и вот они получили общий секретный ключ abP. Ура!
Victor Kleptsyn
М
15:16
Математические байки
Да — естественно, поскольку степень a (я буду писать именно «степень», а не «множитель», потому что хочу думать о точках эллиптической кривой как о группе, пусть и коммутативной) большая, то aP вычисляется не как P+P+…+P сложением a раз, а так же, как любая другая большая степень в группе — чередой удвоений (2^100 P =2 (2(…(2 P))) ), разложением a в двоичную запись и сложением соответствующих удвоений.
Собственно, если бы степень a была столь маленькой, что можно было бы до неё «досчитать» просто сложением P+P+…+P, то это же мог бы проделать и атакующий — складывать P, пока не увидит совпадающий с переданным по открытому каналу результатом aP. И всё, атакующий знает секрет a.
Собственно, если бы степень a была столь маленькой, что можно было бы до неё «досчитать» просто сложением P+P+…+P, то это же мог бы проделать и атакующий — складывать P, пока не увидит совпадающий с переданным по открытому каналу результатом aP. И всё, атакующий знает секрет a.
Victor Kleptsyn
М
15:19
Математические байки
(см.: https://en.wikipedia.org/wiki/Elliptic-curve_Diffie%E2%80%93Hellman#Key_establishment_protocol )
Victor Kleptsyn
М
15:22
Математические байки
Естественно, что за всем этим стоит ещё безумное количество деталей — в которые я вдаваться не буду; оставлю тут только ещё две ссылки:
https://en.wikipedia.org/wiki/Curve25519 — одна конкретная эллиптическая кривая. Вот прямо явно выписанная:
https://en.wikipedia.org/wiki/Curve25519 — одна конкретная эллиптическая кривая. Вот прямо явно выписанная:
Victor Kleptsyn
М
15:31
Математические байки
https://en.wikipedia.org/wiki/Dual_EC_DRBG — а это к тому, что выбор публичной точки/кривой это вопрос тонкий... Цитата из Брюса Шнайдера, https://www.schneier.com/blog/archives/2013/12/nsa_spying_who.html :
Victor Kleptsyn
М
М
15:35
Математические байки
Я не знаю, и не могу знать, так ли это — повторюсь, совсем не моя область — и что специалисты знают сейчас, шесть лет спустя. Но возможности "плохих кривых" как минимум вполне обсуждаемы:
Victor Kleptsyn
М
М
15:37
Математические байки
Вот. Несмотря на все эти тонкости — по крайней мере, как в принципе работают эллиптические кривые "на стороне общающихся", мы посмотрели.
А теперь давайте вернёмся к другой математике, к обещанному в самом начале методу Ленстры : к эллиптическим кривым на стороне нападающего в классической задаче разложения на множители.
А теперь давайте вернёмся к другой математике, к обещанному в самом начале методу Ленстры : к эллиптическим кривым на стороне нападающего в классической задаче разложения на множители.
Victor Kleptsyn
М
16:57
Математические байки
Итак, пусть у нас есть большое число N, и пусть для простоты оно есть произведение двух простых, N=pq.
Китайская теорема об остатках учит нас, что кольцо вычетов по модулю N это не поле -- но декартово произведение двух полей, вычетов по модулю p и по модулю q. И "эллиптическая кривая", которую мы зададим каким-нибудь уравнением, будет декартовым произведением того, что это уравнение задаёт по модулю p и по модулю q.
Китайская теорема об остатках учит нас, что кольцо вычетов по модулю N это не поле -- но декартово произведение двух полей, вычетов по модулю p и по модулю q. И "эллиптическая кривая", которую мы зададим каким-нибудь уравнением, будет декартовым произведением того, что это уравнение задаёт по модулю p и по модулю q.
Victor Kleptsyn
М
16:58
Математические байки
Пусть у нас есть такая кривая и точка Q на ней.
Victor Kleptsyn
М
17:02
Математические байки
Причём кривую мы будем брать вида y^2=P(x) -- с нулём на "вертикальной бесконечности".
Victor Kleptsyn
М
17:24
Математические байки
Давайте умножать точку Q на разные множители -- в групповом смысле, возводить её в степень, причём не 2-3-4, а с большим количеством разных делителей. Если бы у нас и впрямь была группа -- то мы бы в какой-то момент ("выбрав" все делители порядка Q) пришли бы в нейтральный элемент -- то есть улетели бы на бесконечность.
Victor Kleptsyn
М
17:24
Математические байки
Но у нас такая картина происходит с одной кривой mod p, и с другой mod q.
Victor Kleptsyn
М
17:25
Математические байки
Что, если мы уже исчерпали порядок Q по одному модулю, но не по другому?
Victor Kleptsyn
27 February 2020
М
08:39
Математические байки
Формула для суммы точек рациональная -- там есть знаменатель:
Victor Kleptsyn
М
08:39
Математические байки
Когда мы убегаем на бесконечность (как раз сваливаясь в нейтральный элемент группы) -- он обращается в ноль.
Victor Kleptsyn
М
08:40
Математические байки
А вообще, когда мы делим в кольце вычетов по модулю n, мы вычисляем алгоритмом Евклида обратный элемент к знаменателю D (после чего соотношение aD-bn=1 как раз и говорит, что 1/D = a по модулю n).
Victor Kleptsyn
М
08:40
Математические байки
In reply to this message
И когда мы по модулю p убегаем на бесконечность, а по модулю q нет — знаменатель по модулю p ноль, а по модулю q нет. И алгоритм Евклида вместо 1 выдаёт нам p — то есть мы нашли на делитель n. Ура!
Victor Kleptsyn
М
08:45
Математические байки
Вот такая прекрасная история — эллиптические кривые приводят к тому, что поскладывав точки на эллиптической кривой, мы «естественным образом» натыкаемся на делитель n.
Victor Kleptsyn
М
10:28
Математические байки
Кстати — ещё можно спросить, а как мы вообще берём пару из эллиптической кривой и точки на ней? Скажем, если мы сначала напишем уравнение кривой,
y^2=x^3+ax+b,
то неясно, как на ней искать точки. Если выбрать x и пытаться извлечь квадратный корень по модулю n из правой части — так это задача более-менее той же огромной сложности (потому что по модулю n=pq разных квадратных корней 4, а не 2, и найти для m^2 два других корня, кроме (m,-m), равносильно разложению n на множители).
Но есть простой ответ: можно, как тот ковбой из анекдота, сначала стрелять, а потом уже рисовать круги вокруг попаданий. Берём любые (x,y,a), и полагаем b:=y^2-x^3-ax. Готово, у нас есть и эллиптическая кривая, и точка (x,y) на ней.
y^2=x^3+ax+b,
то неясно, как на ней искать точки. Если выбрать x и пытаться извлечь квадратный корень по модулю n из правой части — так это задача более-менее той же огромной сложности (потому что по модулю n=pq разных квадратных корней 4, а не 2, и найти для m^2 два других корня, кроме (m,-m), равносильно разложению n на множители).
Но есть простой ответ: можно, как тот ковбой из анекдота, сначала стрелять, а потом уже рисовать круги вокруг попаданий. Берём любые (x,y,a), и полагаем b:=y^2-x^3-ax. Готово, у нас есть и эллиптическая кривая, и точка (x,y) на ней.
Victor Kleptsyn
М
10:45
Математические байки
Кстати — как утверждает эта (https://members.loria.fr/PZimmermann/records/top50.html ) таблица рекордов, самое большое число (с большими делителями), разложенное на множители с помощью эллиптических кривых, состоит из 83 цифр (и является одним из сомножителей в разложении 7^337+1).
Victor Kleptsyn
М
10:47
Математические байки
И это ещё не самый большой успех факторизации (ибо метод Ленстры не самый быстрый, а для больших чисел лишь третий с конца ) —
Victor Kleptsyn
М
М
10:52
Математические байки
Ещё более впечатляющий успех — состоящее из 240 цифр (795 бит!) число RSA-240 было разложено на множители в ноябре 2019: https://caramba.loria.fr/dlp240-rsa240.txt
Victor Kleptsyn
4 March 2020
М
11:56
Математические байки
Вдогонку к предыдущему рассказу, вспомнились "25 этюдов о шифрах" (https://math.ru/lib/files/pdf/misc/25etudes.pdf ) — полученная когда-то давным-давно в качестве приза на какой-то олимпиаде. :)
Метода Ленстры там нет — но вот протокол Диффи-Хеллмана через степени есть (раздел 3.6):
Метода Ленстры там нет — но вот протокол Диффи-Хеллмана через степени есть (раздел 3.6):
Victor Kleptsyn
5 March 2020
М
20:39
Математические байки
Сегодняшняя байка совсем простая и короткая — это рассказ про иглу Бюффона. Допустим, у нас есть "лист в линейку" — на плоскости проведены параллельные прямые с расстоянием 1 между соседними, — и мы кидаем случайным образом на этот лист иголку единичной длины. С какой вероятностью она зацепит одну из линий?
Victor Kleptsyn
М
20:40
Математические байки
Ответ: 2/π.
А если расстояние между линиями равно D, а длина иголки L, и L<D, то вероятность равна 2L/πD.
А если расстояние между линиями равно D, а длина иголки L, и L<D, то вероятность равна 2L/πD.
Victor Kleptsyn
М
20:40
Математические байки
Не то, чтобы это было сложно посчитать (там один простой интеграл) — но интересно, что ответ можно получить вообще без выкладок!
Victor Kleptsyn
М
20:41
Математические байки
А именно: давайте кидать кривую иголку произвольной формы — но смотреть уже не на вероятность пересечения, а на математическое ожидание их количества.
Victor Kleptsyn
М
20:41
Математические байки
Для прямой короткой иголки ничего не изменится: пересечений может быть либо 0, либо 1, поэтому вероятность и математическое ожидание тут совпадают.
Victor Kleptsyn
М
20:47
Математические байки
Так вот, несложно убедиться, что математическое ожидание пропорционально её длине. Потому что — если разбить иголку на несколько частей, то матожидание числа пересечений для всей иголки равно сумме матожиданий для частей (потому что каждая отдельная часть при бросании всей иголки тоже приземляется случайным образом; разные части зависимы, конечно, но аддитивности матожидания это не мешает).
Victor Kleptsyn
М
20:50
Математические байки
Поэтому для прямой иголки число пересечений это аддитивная функция от её длины L — то есть c*L для некоторой константы c (если считать, что расстояние D между линиями фиксировано).
А любую (гладкую) иголку можно разбить на много-много маленьких почти-прямых кусочков, и их будет столько же, сколько и для прямой иголки такой же длины — а значит, и матожидание будет таким же.
А любую (гладкую) иголку можно разбить на много-много маленьких почти-прямых кусочков, и их будет столько же, сколько и для прямой иголки такой же длины — а значит, и матожидание будет таким же.
Victor Kleptsyn
М
20:51
Математические байки
Итак, матожидание числа пересечений для кривой длины L равно c*L — где c от кривой не зависит. Осталось его найти.
Victor Kleptsyn
М
20:51
Математические байки
Так вот, давайте возьмём в качестве кривой иглы — окружность диаметра, равного расстоянию между линиями!
Victor Kleptsyn
М
20:52
Математические байки
Она всегда пересекает линии ровно в двух точках.
Victor Kleptsyn
М
20:52
Математические байки
Значит, матожидание равно 2. Ну а длина этой кривой — L=πD. Отсюда c=2/(πD).
Victor Kleptsyn
М
20:53
Математические байки
И тем самым уже для любой кривой длины L матожидание числа пересечений равно 2L/πD.
Victor Kleptsyn
М
20:53
Математические байки
Всё!
Victor Kleptsyn
9 March 2020
М
13:08
Математические байки
Эта история, которую я узнал из лекции Ингрид Добеши (https://www.youtube.com/watch?v=Z19uz6Bol3I&feature=youtu.be&t=160 ) на ICM-2018 в Рио — не совсем про математику, а про её применение в искусстве.
Там было несколько сюжетов, но один из них — про холсты картин и преобразование Фурье. И мне кажется, это очень крутая история. (Я её пересказывал некоторое время назад, но в более узком кругу, и поскольку очень эту историю люблю — позволю себе повторить и тут.)
Там было несколько сюжетов, но один из них — про холсты картин и преобразование Фурье. И мне кажется, это очень крутая история. (Я её пересказывал некоторое время назад, но в более узком кругу, и поскольку очень эту историю люблю — позволю себе повторить и тут.)
Victor Kleptsyn
М
13:11
Математические байки
Картины пишут на холстах, на ткани (хорошо, не только — но забудем про все остальные варианты). Причём эту ткань обрабатывают свинцовыми белилами — чтобы она впитывала краску чуть менее сильно. А свинцовые белила (и потому и нити холста) хорошо видны на рентгене:
Victor Kleptsyn
М
13:12
Математические байки
(Тут и позитив и негатив.)
Victor Kleptsyn
М
13:18
Математические байки
Образуется периодическая структура. И несложно объяснить компьютеру, как искать её периоды, вертикальный и горизонтальный: через преобразование Фурье.
(Коллега комментирует, что можно научить компьютер считать частоту и ещё разными способами, а преобразование Фурье это скорее тот самый универсальный молоток, которым можно делать много что, в том числе и это; но раз в лекции Добеши Фурье, то я скажу "Фурье".)
(Коллега комментирует, что можно научить компьютер считать частоту и ещё разными способами, а преобразование Фурье это скорее тот самый универсальный молоток, которым можно делать много что, в том числе и это; но раз в лекции Добеши Фурье, то я скажу "Фурье".)
Victor Kleptsyn
М
13:19
Математические байки
Так вот, самое интересное.
Холст тех времён штука неидеальная, расстояния между нитями могут быть чуть больше или чуть меньше, угол может быть чуть больше или чуть меньше, и так далее. Можно раскрасить картину по таким характеристикам — и получить раскраски для горизонтальных нитей и для вертикальных:
Холст тех времён штука неидеальная, расстояния между нитями могут быть чуть больше или чуть меньше, угол может быть чуть больше или чуть меньше, и так далее. Можно раскрасить картину по таким характеристикам — и получить раскраски для горизонтальных нитей и для вертикальных:
Victor Kleptsyn
М
13:20
Математические байки
Берём две картины, которые Ван Гог нарисовал примерно в одно и то же время. Смотрим на раскраску —
Victor Kleptsyn
М
13:21
Математические байки
Он (как и многие художники) покупал холст в больших рулонах, а потом из рулона вырезал кусок для картины!
И все эти параметры, все эти раскраски оказываются "цифровыми отпечатками" рулонов холста.
И все эти параметры, все эти раскраски оказываются "цифровыми отпечатками" рулонов холста.
Victor Kleptsyn
М
13:22
Математические байки
То есть в руках у искусствоведов оказывается возможность выяснять, что две разные картины нарисованы на кусках холста, вырезанных из одного и того же большого рулона.
Victor Kleptsyn
М
13:23
Математические байки
И раскраски приводят, например, вот к такому. Смотрим раз:
Victor Kleptsyn
М
13:24
Математические байки
Смотрим два:
Victor Kleptsyn
М
13:25
Математические байки
Вуаля: эти шесть картин Ван Гог нарисовал на кусках холста, вырезанных из одного и того же большого рулона — и мы даже знаем, как они в этом рулоне располагались!
А вот и сами эти картины:
А вот и сами эти картины:
Victor Kleptsyn
М
13:28
Математические байки
Вот тут есть ещё аналогичная картинка —
https://www.vangoghmuseum.nl/en/knowledge-and-research/research-projects/automated-canvas-analysis/second-phase-automated-canvas-analysis-project?v=1
https://www.vangoghmuseum.nl/en/knowledge-and-research/research-projects/automated-canvas-analysis/second-phase-automated-canvas-analysis-project?v=1
Victor Kleptsyn
М
13:29
Математические байки
Кстати, там можно увидеть, что одни картины относительно других (для совпадения "как их холст вырезался из рулона") приходится поворачивать или переворачивать.
Victor Kleptsyn
М
13:35
Математические байки
А ещё это может быть серьёзным аргументов в аттрибуции картин: Женя Смирнов год назад рассказывал, что на выставке Лейденской коллекции в Москве ( https://www.hermitagemuseum.org/wps/portal/hermitage/what-s-on/temp_exh/2018/rembrandttime/ ) видел у одной из картин табличку — "раньше в её авторстве сомневались, но теперь установлено, что она написана на куске холста из того же рулона, что и бесспорный Вермеер".
Victor Kleptsyn
М
13:40
Математические байки
А это из статьи "Canvas Matches in Vermeer: A Case Study in the Computer Analysis of Fabric Supports" — https://people.ece.cornell.edu/johnson/LiedtkeMMJ.pdf
Victor Kleptsyn
М
13:44
Математические байки
Там же (с. 102) обсуждение, что для датировки такое совпадение не очень помогает: после смерти Вермеера в его мастерской обнаружили десять холстов, и учитывая краткость описания, имеются в виду просто подготовленные холсты, а не законченные картины:
Victor Kleptsyn
М
13:47
Математические байки
И [я всё ещё пересказываю статью] поскольку Вермеер писал хорошо если три картины в год (а тут десять холстов) — датировка по близости холстов не будет очень надёжной:
Victor Kleptsyn
М
13:49
Математические байки
Вот такая история. Мне кажется, несмотря на все ограничения — это очень круто!
Victor Kleptsyn
14 March 2020
М
16:05
Математические байки
Дорогие читатели, вас уже больше тысячи, и это безумно приятно; спасибо вам!
Ещё — Григорий Мерзон выложил зеркало-архив этого канала за 2019 год, с оглавлением для упрощения навигации, и за это ему большое спасибо! Так что теперь можно посмотреть первые байки без мучительного листания назад:
http://dev.mccme.ru/~merzon/mirror/mathtabletalks/
Ещё — Григорий Мерзон выложил зеркало-архив этого канала за 2019 год, с оглавлением для упрощения навигации, и за это ему большое спасибо! Так что теперь можно посмотреть первые байки без мучительного листания назад:
http://dev.mccme.ru/~merzon/mirror/mathtabletalks/
Victor Kleptsyn
М
16:06
Математические байки
Сегодня Pi Day (потому что 3/14), так что сегодняшняя байка будет посвящена числу π — но не только.
А именно — как все знают, π иррационально и даже трансцендентно. И вот доказательства его иррациональности я хочу обсудить.
А именно — как все знают, π иррационально и даже трансцендентно. И вот доказательства его иррациональности я хочу обсудить.
Victor Kleptsyn
М
16:07
Математические байки
Первое доказательство — то, которое чаще всего рассказывается в университете. Оно довольно короткое, но начинается с действия, которое нужно запомнить (и этим мне не очень нравится).
Victor Kleptsyn
М
16:07
Математические байки
А именно — пусть π=a/b.
Давайте возьмём какое-нибудь натуральное n и посмотрим на функцию
f(x)=x^n (a-bx)^n / n!
Давайте возьмём какое-нибудь натуральное n и посмотрим на функцию
f(x)=x^n (a-bx)^n / n!
Victor Kleptsyn
М
М
16:08
Математические байки
Умножим эту функцию на sin x и по [0,π] проинтегрируем. Что получится?
Victor Kleptsyn
М
16:12
Математические байки
С одной стороны, интеграл считается явно — кучей-кучей интегрирования по частям (как и любой интеграл от произведения многочлена на экспоненту). Получим F(0)+F(π), где F(x)=f(x)-f''(x)+f''''(x) - ... .
Потому что первообразная будет
-F(x) cos x +G(x) sin x,
где в G собраны нечётные производные f (тем самым, G=F', но это неважно) — но синус в 0 и π обращается в ноль, так что для определённого интеграла по [0,π] второе слагаемое роли не играет.
Потому что первообразная будет
-F(x) cos x +G(x) sin x,
где в G собраны нечётные производные f (тем самым, G=F', но это неважно) — но синус в 0 и π обращается в ноль, так что для определённого интеграла по [0,π] второе слагаемое роли не играет.
Victor Kleptsyn
М
16:14
Математические байки
И этот интеграл тем самым оказывается целым!
Victor Kleptsyn
М
16:15
Математические байки
Потому что в числителе функции f стоят n-е степени обращающихся в ноль на концах отрезка функций. Поэтому, чтобы получить ненулевой вклад в F(.) в каком-нибудь из концов отрезка (x=0 или x=π=a/b), нужно соответствующую функцию (x или a-bx соответственно) "додифференцировать" до нулевой степени. Но тогда n! в знаменателе исчезает.
Victor Kleptsyn
М
16:16
Математические байки
А с другой стороны, при n, стремящемся к бесконечности, факториал в знаменателе забивает экспоненту в числителе. Поэтому подынтегральная функция равномерно стремится к 0.
И при достаточно большом n значение интеграла одновременно целое и заключено между 0 и 1. Противоречие.
И при достаточно большом n значение интеграла одновременно целое и заключено между 0 и 1. Противоречие.
Victor Kleptsyn
М
16:19
Математические байки
Вот. Это доказательство короткое и хорошее — но его сложно придумать "с нуля". А есть исторически первое доказательство Ламберта, придуманное в 1760-е (и, собственно, ради него я эту байку и рассказываю). В котором есть одна идея — но смысловая — и из которого много что ещё получается.
Victor Kleptsyn
М
16:19
Математические байки
Эта идея — "давайте разложим тангенс в цепную дробь". И да, в цепные дроби можно раскладывать не только числа, но и функции.
Victor Kleptsyn
М
16:20
Математические байки
А именно: как устроено обычное разложение в цепную дробь? Есть "большие и дискретные" целые числа Z, и есть "маленькие" числа — полуинтервал A=[0,1). Берём какое-то начальное число, вычитанием элемента из Z приносим его на A, "переворачиваем" применением 1/x, и так повторяем много-много раз.
Victor Kleptsyn
М
16:20
Математические байки
Так вот, давайте работать с функциями, определёнными (и "хорошими"-аналитическими) в окрестности точки x=0.
В роли целых чисел как чего-то "большого" выступит кольцо R[1/x] многочленов от (1/x). А в роли "маленького" множества A — функции, обращающиеся в точке x=0 в ноль.
В роли целых чисел как чего-то "большого" выступит кольцо R[1/x] многочленов от (1/x). А в роли "маленького" множества A — функции, обращающиеся в точке x=0 в ноль.
Victor Kleptsyn
М
16:22
Математические байки
Да, пока я не убежал вперёд — если вдруг вы не видели брошюру В. И. Арнольда "Цепные дроби", https://www.mccme.ru/mmmf-lectures/books/#book-14 — то я очень советую её посмотреть!
Victor Kleptsyn
М
16:26
Математические байки
Так вот, давайте применим алгоритм разложения к функции f(x)=tg x. Почему? Ну точно так же, как в ряд Тейлора, когда он придуман, имеет смысл пытаться раскладывать всё подряд — вдруг где что красивое попадётся, — и запоминать удачные результаты, точно так же почему бы в цепную дробь не пораскладывать всё подряд, например, тангенс?
Victor Kleptsyn
М
16:27
Математические байки
Итак, функция tg x уже "маленькая":
tg x = x + x^3/3+ ... ;
перевернём её. Получается котангенс.
ctg x при x->0 "взрывается" как 1/x; вычтем и посмотрим, что останется:
ctg x - 1/x = -x/3 + ... ;
(упражнение — проверьте!).
tg x = x + x^3/3+ ... ;
перевернём её. Получается котангенс.
ctg x при x->0 "взрывается" как 1/x; вычтем и посмотрим, что останется:
ctg x - 1/x = -x/3 + ... ;
(упражнение — проверьте!).
Victor Kleptsyn
М
16:28
Математические байки
Перевернув, получаем (-3/x). Продолжая в том же духе — а это, в каком-то смысле, чисто механическая деятельность — находим первые несколько членов разложения (не касаясь пока вопроса его сходимости):
Victor Kleptsyn
М
16:30
Математические байки
Первые три элемента цепной дроби выглядят достаточно заманчиво, чтобы посчитать следующий. И действительно —
Victor Kleptsyn
М
16:31
Математические байки
Итак, вне зависимости от собственно иррациональности числа π, с которой мы начинали, мы (пока чисто экспериментально) обнаружили замечательный факт: функция тангенс очень красиво разлагается в цепную дробь.
Victor Kleptsyn
М
18:18
Математические байки
Теперь нам осталось сделать две вещи:
1) доказать это разложение (что мы отложим напоследок)
и
2) понять, какое же отношение оно имеет к иррациональности π.
Но даже прежде, чем всё это сделать — давайте "уйдём в радиалку" и вместо функции "тангенс" посмотрим на функцию "тангенс гиперболический".
1) доказать это разложение (что мы отложим напоследок)
и
2) понять, какое же отношение оно имеет к иррациональности π.
Но даже прежде, чем всё это сделать — давайте "уйдём в радиалку" и вместо функции "тангенс" посмотрим на функцию "тангенс гиперболический".
Victor Kleptsyn
М
18:18
Математические байки
Можно повторить те же выкладки (и опять угадать ответ), а можно сказать, что tanh x = i tg (x/i), и подставив это в предыдущее разложение, увидеть, что просто знаки перед дробями поменяются:
Victor Kleptsyn
М
18:19
Математические байки
А теперь внимание, трюк. Подставим x=1/2:
Victor Kleptsyn
М
18:20
Математические байки
С одной стороны, результат нам интересен:
Victor Kleptsyn
М
М
18:21
Математические байки
С другой, мы получаем (если верить в сходимость) самую настоящую, классическую цепную дробь — ведь элементы (2k+1)/x-то уже все натуральные:
Victor Kleptsyn
М
18:23
Математические байки
И вот мы получили цепную дробь если не для e, то для связанного с ним числа, (e-1)/(e+1).
Victor Kleptsyn
М
18:33
Математические байки
И не совсем мгновенно, но не очень сложно перейти от (e-1)/(e+1) к цепной дроби для собственно e. Которая за счёт этого перехода немного меняется и в дополнение к арифметической прогрессии (со вдвое меньшей разностью) начинает "заикаться единицами":
e= [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8,...]
e= [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8,...]
Victor Kleptsyn
М
19:17
Математические байки
Да — не могу не вставить сюда формулы из исходного мемуара Ламберта, http://www.bibnum.education.fr/mathematiques/theorie-des-nombres/lambert-et-l-irrationalite-de-p-1761 — разложение для тангенса
Victor Kleptsyn
М
19:18
Математические байки
и формулу для цепной дроби для числа, связанного с e:
Victor Kleptsyn
М
19:20
Математические байки
In reply to this message
Собственно, переход, о котором я говорил выше, в основном связан с переходом от цепной дроби для x к цепной дроби для 2x — который прост, но неочевиден. Но к этому мы вернёмся потом...
Victor Kleptsyn
М
19:22
Математические байки
Кстати, если вы читаете по-французски — очень интересно Ламберта читать. Удивительным образом, всё понятно — но постоянно сбивает с толку очень "вытянутое" написание буквы "s", в результате она кажется похожей на "f". Вот, например, в разложениях для синуса и косинуса:
Victor Kleptsyn
М
19:24
Математические байки
In reply to this message
Теперь — собственно, главный шаг за сегодня.
Давайте применим это разложение к исходной цели — к иррациональности π. И для этого вспомним, что
tg π/4 = 1.
Если бы π было рациональным, то рациональным было бы и π/4. Пусть π/4=a/b.
Давайте применим это разложение к исходной цели — к иррациональности π. И для этого вспомним, что
tg π/4 = 1.
Если бы π было рациональным, то рациональным было бы и π/4. Пусть π/4=a/b.
Victor Kleptsyn
М
19:25
Математические байки
Подставим это в цепную дробь для тангенса — и получим бесконечную цепную дробь для рационального числа 1:
Victor Kleptsyn
М
19:28
Математические байки
Правда, пока тут есть и минусы, и элементы лишь рациональные. Поборемся со второй проблемой — умножим у каждой дроби числитель и знаменатель на a. И я опять не могу не процитировать Ламберта (правда, с Ф=a и w=b):
Victor Kleptsyn
М
19:30
Математические байки
В наших обозначениях —
Victor Kleptsyn
М
19:33
Математические байки
In reply to this message
И наверное, вы уже догадались, что мы сейчас сделаем: скажем, что такой дроби для рационального числа 1 не может быть. А именно — оборвём её на каком-нибудь глубоком уровне n. Посмотрим, насколько хорошо получающееся рациональное число приближает результат.
Victor Kleptsyn
М
19:35
Математические байки
С одной стороны, рациональные числа не могут слишком хорошо приближать друг друга (именно так доказывается, например, что e иррационально). И в частности, если мы приблизили 1=tg a/b рациональным числом P/Q, и при этом не попали точно в единицу, то ошибка не может быть меньше 1/Q.
Victor Kleptsyn
М
19:38
Математические байки
С другой, обычная цепная дробь приближает результат с ошибкой не больше 1/Q^2. Если бы для нашей дроби — у которой числители уже не 1, a a^2 (или, точнее, -a^2, если принимать во внимание минусы) — что-нибудь подобное продолжало выполняться, то это была бы победа. Так вот, тут всё чуть хуже, но нам всё равно хватит.
Victor Kleptsyn
М
22:04
Математические байки
In reply to this message
А именно: как многие знают, если обозначить через p_n/q_n дробь, получающуюся при обрыве обычной цепной дроби [для какого-то числа x] на уровне n (такие дроби называются подходящими ), то для две соседние подходящие дроби p_n/q_n и p_{n+1}/q_{n+1} приближают x с разных сторон, а разница между ними "наименьшая возможная":
| p_n/q_n - p_{n+1}/q_{n+1} | = 1/(q_n q_{n+1}).
В нашем случае окажется, что в числителе уже не 1 — а произведение числителей (одного a и остальных a^2). И это само по себе заслуживает того, чтобы с этим разобраться, и это потребует экскурсии в цепные дроби.
| p_n/q_n - p_{n+1}/q_{n+1} | = 1/(q_n q_{n+1}).
В нашем случае окажется, что в числителе уже не 1 — а произведение числителей (одного a и остальных a^2). И это само по себе заслуживает того, чтобы с этим разобраться, и это потребует экскурсии в цепные дроби.
Victor Kleptsyn
М
22:06
Математические байки
Если в это поверить — то разница между двумя последовательными приближениями P_n/Q_n и P_{n+1}/Q_{n+1} для tg(a/b) будет
a^{2n+1}/(Q_n Q_{n+1}).
a^{2n+1}/(Q_n Q_{n+1}).
Victor Kleptsyn
М
22:13
Математические байки
При этом знаменатели Q_n растут очень быстро, факториально (что мы ещё увидим) — из-за того, что растут элементы цепной дроби b, 3b, 5b, 7b,...
Поэтому отношение a^{2n+1}/Q_{n+1} будет стремиться к нулю (экспонента проигрывает факториалу).
Поэтому отношение a^{2n+1}/Q_{n+1} будет стремиться к нулю (экспонента проигрывает факториалу).
Victor Kleptsyn
М
22:15
Математические байки
И очень естественно, что и разница
|tg (a/b) - P_n/Q_n|
тоже будет убывать с примерно такой же скоростью, как расстояние "до следующего приближения"
|P_n/Q_n - P_{n+1}/Q_{n+1}|;
например, как только следующее расстояние всегда вдвое меньше предыдущего, сумма ряда из расстояний максимум вдвое превышает первое слагаемое, и потому при всех достаточно больших n
|tg (a/b) - P_n/Q_n| < 2(a^{2n+1}/Q_{n+1}) / Q_n.
|tg (a/b) - P_n/Q_n|
тоже будет убывать с примерно такой же скоростью, как расстояние "до следующего приближения"
|P_n/Q_n - P_{n+1}/Q_{n+1}|;
например, как только следующее расстояние всегда вдвое меньше предыдущего, сумма ряда из расстояний максимум вдвое превышает первое слагаемое, и потому при всех достаточно больших n
|tg (a/b) - P_n/Q_n| < 2(a^{2n+1}/Q_{n+1}) / Q_n.
Victor Kleptsyn
М
22:20
Математические байки
В частности, как только числитель становится меньше 1 — мы получаем противоречие с tg(a/b)=1.
И точно так же доказывается, что тангенс никакого рационального числа [радиан], кроме 0, не может быть рациональным. Потому что дробь c/d нельзя (без "идеального попадания") приблизить дробью p/q с точностью, лучшей, чем (1/d)/q, то есть константа/знаменатель. А у нас оборванная цепная дробь даёт приближения вида
"сколь угодно малый числитель"/Q_n.
То есть лучше, чем можно.
И точно так же доказывается, что тангенс никакого рационального числа [радиан], кроме 0, не может быть рациональным. Потому что дробь c/d нельзя (без "идеального попадания") приблизить дробью p/q с точностью, лучшей, чем (1/d)/q, то есть константа/знаменатель. А у нас оборванная цепная дробь даёт приближения вида
"сколь угодно малый числитель"/Q_n.
То есть лучше, чем можно.
Victor Kleptsyn
М
22:39
Математические байки
И на этой цитате из Ламберта — больше, чем 250-летней давности! — я на сегодня завершаю дозволенные речи; а в следующий раз мы посмотрим на красоту цепных дробей (и их де-проективизации).
Victor Kleptsyn
Deleted Account pinned this message
17 March 2020
М
19:51
Математические байки
In reply to this message
Продолжим?
Наш следующий шаг — разобраться с цепными дробями. Как для того, чтобы разобраться с разложением тангенса — так и для того, чтобы доказать утверждение выше про разность соседних цепных дробей.
И первое и самое важное понимание тут — это переход от дробно-линейных (проективных) отображений к линейным (что можно жаргонно назвать словом "де-проективизация").
Наш следующий шаг — разобраться с цепными дробями. Как для того, чтобы разобраться с разложением тангенса — так и для того, чтобы доказать утверждение выше про разность соседних цепных дробей.
И первое и самое важное понимание тут — это переход от дробно-линейных (проективных) отображений к линейным (что можно жаргонно назвать словом "де-проективизация").
Victor Kleptsyn
М
19:52
Математические байки
А именно — вместо того, чтобы работать с вещественным числом x — будем работать с вектором v=(a,b), у которого x это отношение координат: x=a/b.
И ясно, что этот вектор можно заменить на любой пропорциональный — отношение координат от этого не изменится.
И ясно, что этот вектор можно заменить на любой пропорциональный — отношение координат от этого не изменится.
Victor Kleptsyn
М
19:53
Математические байки
Так вот — в таком случае, например, разложение в цепную дробь становится применением алгоритма Евклида к паре (x,1). Действительно,
*) вычитание из x его целой части k=[x] соответствует переходу (a,b) -> (a-kb,b),
*) а переход от x к 1/x — переходу (a,b) -> (b,a).
*) вычитание из x его целой части k=[x] соответствует переходу (a,b) -> (a-kb,b),
*) а переход от x к 1/x — переходу (a,b) -> (b,a).
Victor Kleptsyn
М
19:53
Математические байки
После n шагов разложения в цепную дробь у нас образуется выражение вот такого вида —
Victor Kleptsyn
М
19:54
Математические байки
И в силу вышесказанного на него можно смотреть как на линейное преобразование — переводящее прямую a=x_{n+1}*b в прямую a=x*b.
Victor Kleptsyn
М
19:55
Математические байки
При этом дробь p_n/q_n, полученная обрыванием цепной дроби на a_n, соответствует подстановке x_n=0 — или, в линейных терминах, вектор (p_n,q_n) является образом вектора (0,1). А обрыв на a_{n-1} — подстановке значения x_n=бесконечности; в линейных терминах — образу вектора (1,0).
Victor Kleptsyn
М
19:55
Математические байки
Поэтому линейное преобразование, которое мы только что упомянули, имеет в качестве коэффициентов p_n, q_n, p_{n-1} и q_{n-1}:
Victor Kleptsyn
М
М
19:57
Математические байки
А следующая матрица получается из предыдущей умножением справа на то, что отвечает последнему шагу, A_{n+1}=A_n R_{n+1}.:
Victor Kleptsyn
М
М
19:58
Математические байки
На языке векторов v_n=(p_n, q_n) это соответствует линейному соотношению —
v_{n+1}=a_{n+1}v_n + v_{n-1}.
Потому что мы смотрим на образ вектора (1, a_{n+1}) под действием всей предыдущей матрицы.
v_{n+1}=a_{n+1}v_n + v_{n-1}.
Потому что мы смотрим на образ вектора (1, a_{n+1}) под действием всей предыдущей матрицы.
Victor Kleptsyn
М
20:00
Математические байки
И я помню, как в своё время меня удивили рекуррентные соотношения на подходящие дроби — почему-то одинаковые для числителей и знаменателей:
Victor Kleptsyn
М
М
20:00
Математические байки
Так вот — потому что это на самом деле соотношения на вектора v_n, у которых числители p_n и знаменатели q_n это координаты.
Victor Kleptsyn
М
20:01
Математические байки
Я тут пользуюсь случаем порекламировать замечательную брошюру В.И. Арнольда, "Цепные дроби" (https://www.mccme.ru/free-books/mmmf-lectures/book.14-full.pdf ) — с соответствующей картинкой на с. 7:
Victor Kleptsyn
М
20:12
Математические байки
Так вот — после такой линейной интерпретации, например, становится очень понятно, почему разница соседних подходящих дробей это плюс-минус единица, делённая на произведение знаменателей:
Victor Kleptsyn
М
М
20:13
Математические байки
Потому что в числителе разности дробей
a/b-c/d = (ad-bc)/bd
стоит определитель ad-bc — он же ориентированная площадь параллелограмма, натянутого на вектора (a,b) и (c,d):
a/b-c/d = (ad-bc)/bd
стоит определитель ad-bc — он же ориентированная площадь параллелограмма, натянутого на вектора (a,b) и (c,d):
Victor Kleptsyn
М
20:14
Математические байки
Когда мы прибавляем к одному из векторов другой, умноженный на константу, площадь не меняется; когда меняем их местами — меняет знак.
Victor Kleptsyn
М
20:14
Математические байки
In reply to this message
Нет, конечно, из рекуррентных соотношений это тоже немедленно следует, но это объяснение, мне кажется, более правильное.
Victor Kleptsyn
М
20:16
Математические байки
In reply to this message
Конечно же, ещё лучше сказать, что числитель
p_{n-1} q_n -p_n q_{n-1}
это определитель нашей матрицы A_n, который тем самым равен произведению определителей R_n — каждый из которых равен (-1).
p_{n-1} q_n -p_n q_{n-1}
это определитель нашей матрицы A_n, который тем самым равен произведению определителей R_n — каждый из которых равен (-1).
Victor Kleptsyn
М
20:18
Математические байки
Так вот — а давайте теперь посмотрим на наши модифицированные цепные дроби, у которых каждый раз не "+1/что-то там", а "-a^2/что-то там".
Victor Kleptsyn
М
20:22
Математические байки
И вообще на дроби вида —
Victor Kleptsyn
М
20:23
Математические байки
Если смотреть с точки зрения "модифицированного алгоритма Евклида", то после j-го вычитания мы не просто меняем местами координаты, а умножаем одну из них на c_j.
Victor Kleptsyn
М
20:28
Математические байки
Если смотреть с точки зрения произведения матриц — то мы будем перемножать матрицы вида
Victor Kleptsyn
М
М
20:29
Математические байки
Первая матрица отвечает операции a_n+(...), а вторая — переходу x->c_{n+1}/x.
Victor Kleptsyn
М
20:31
Математические байки
И определитель у такой матрицы равен (-c_{n+1}) — соответственно, мы получаем в качестве числителя разности "подходящих дробей" (получающихся обрубанием на a_n)
P_{n-1}/Q_{n-1} - P_n/Q_n
произведение (-c_j).
P_{n-1}/Q_{n-1} - P_n/Q_n
произведение (-c_j).
Victor Kleptsyn
М
20:35
Математические байки
In reply to this message
Вот отсюда и получается, что в нашем случае, когда все c_j, кроме первого, равны (-a^2), а первый равен (-a), разница "подходящих дробей" P_n/Q_n будет равна
a^{2n+1}/(Q_n Q_{n+1}).
a^{2n+1}/(Q_n Q_{n+1}).
Victor Kleptsyn
М
20:41
Математические байки
Ну а из-за рекуррентных формул знаменатели Q_n растут не медленнее, чем произведения элементов цепной дроби — откуда и следует, что в случае нашей дроби для тангенса (когда это возрастающие нечётные числа*b) отношение a^{2n+1}/Q_{n+1} стремится к 0 (ибо экспонента проигрывает факториалу).
Victor Kleptsyn
М
20:42
Математические байки
Вот мы и разобрались с первой частью "долга" — про то, как ведут себя цепные дроби с не-единичными числителями.
Victor Kleptsyn
М
20:43
Математические байки
Кстати — вообще-то это заслуживает отдельного рассказа, но я упомяну одну страницу из появившихся записок Е. Смирнова о фризах:
Victor Kleptsyn
М
20:45
Математические байки
А к комментарию коллег добавлю, что удивительно, что цепные дроби (а также триангуляции) возникают в задаче, исходно с ними никак не связанной.
Victor Kleptsyn
М
20:45
Математические байки
Н
Непрерывное математическое образование 17.03.2020 17:47:07
https://users.mccme.ru/smirnoff/papers/friezes0317.pdf
записки миникурса Е.Смирнова про фризы и цепные дроби на ЛШСМ-2019 (особых предварительных знаний не требуется, можно читать старшеклассникам)
записки миникурса Е.Смирнова про фризы и цепные дроби на ЛШСМ-2019 (особых предварительных знаний не требуется, можно читать старшеклассникам)
Victor Kleptsyn
М
20:47
Математические байки
In reply to this message
А именно — мы пытаемся расставлять числа в (повёрнутой на 45 градусов) квадратной решётке так, чтобы в любом квадрате разница произведений лево*право и верх*низ равнялась бы 1, начиная с двух горизонталей сначала из 0, потом из 1:
Victor Kleptsyn
М
20:49
Математические байки
0 0 0 0 0 0 0
1 1 1 1 1 1
3 5 5 4 3
1 1 1 1 1 1
3 5 5 4 3
Victor Kleptsyn
М
20:49
Математические байки
Следующий ряд ещё понятно, как заполнить: произведение соседей минус 1:
Victor Kleptsyn
М
20:51
Математические байки
0 0 0 0 0 0 0
1 1 1 1 1 1
3 5 5 4 3
14 24 19 11
1 1 1 1 1 1
3 5 5 4 3
14 24 19 11
Victor Kleptsyn
М
20:53
Математические байки
Но "почему-то" результат и дальше остаётся целым: скажем, в квадрате с верхней вершиной 5 и боковыми 14 и 24 в нижнее число мы должны вписать (14*24-1)/5 — и оно делится нацело!
Victor Kleptsyn
М
20:53
Математические байки
И чем глубже мы спускаемся, тем больше становятся числа, и тем удивительнее делимость...
Victor Kleptsyn
М
20:54
Математические байки
Так вот — там как раз возникают цепные дроби с c_j=-1, дроби Хирцебруха.
Victor Kleptsyn
М
21:02
Математические байки
И много что ещё — но я возвращаюсь обратно к нашей задаче: нам осталось доказать угаданное разложение тангенса в цепную дробь.
Victor Kleptsyn
М
21:31
Математические байки
А именно — мы хотим получить вот такое разложение:
Victor Kleptsyn
М
21:32
Математические байки
Если домножить у каждой дроби числитель и знаменатель на x, то мы переходим к
Victor Kleptsyn
М
21:33
Математические байки
Давайте ещё поделим на x и перевернём дроби:
Victor Kleptsyn
М
21:36
Математические байки
И вот теперь можно запустить "алгоритм Евклида" — для пары из cos x и sin(x)/x.
Victor Kleptsyn
М
21:38
Математические байки
Нам же не обязательно при разложении в цепную дробь начинать с чего-то и 1 — так давайте начинать с такого "вектора" (пусть и с функциями-компонентами) данного направления, с которым нам удобнее всего работать. А уж что приятно разлагать в ряд по x, так это синус и косинус.
Victor Kleptsyn
18 March 2020
М
17:33
Математические байки
Продолжим?
Victor Kleptsyn
М
17:35
Математические байки
In reply to this message
Так вот — именно для такой работы у Ламберта появлялись разложения синуса и косинуса. Потому что зачем работать с рядом Тейлора для тангенса, который ещё и регулярно придётся "переворачивать" (в смысле, переходить от f к 1/f), если можно работать с синусом и косинусом, которые сами по себе замечательные, и вычитать с нужным множителем.
Victor Kleptsyn
М
17:37
Математические байки
В нашем случае мы (идя параллельно Ламберту, но чуть-чуть отклонившись) работаем с функциями
f_0(x)=cos x и f_1(x)=sin(x)/x —
в таком виде итоговое рассуждение окажется более коротким.
f_0(x)=cos x и f_1(x)=sin(x)/x —
в таком виде итоговое рассуждение окажется более коротким.
Victor Kleptsyn
М
17:38
Математические байки
Раскладываем f_0 —
Victor Kleptsyn
М
М
17:39
Математические байки
Раскладываем f_1 —
Victor Kleptsyn
М
М
17:39
Математические байки
Вычитаем f_1 из f_0 (ибо алгоритм Евклида):
Victor Kleptsyn
М
М
17:41
Математические байки
In reply to this message
Свободный член сократился — а у нас цепная дробь с (-x^2) в числителе, так что f_2 это (-1/x^2)*(f_1-f_0):
Victor Kleptsyn
М
М
17:41
Математические байки
Обратите внимание — числители вполне нестрашные.
Victor Kleptsyn
М
17:42
Математические байки
Продолжаем алгоритм Евклида с делением — у f_2 свободный член (1/3), так что из f_1 её нужно вычесть с коэффициентом 3. Получаем:
Victor Kleptsyn
М
М
17:43
Математические байки
Опять-таки, делим на (-x^2), получаем f_3:
Victor Kleptsyn
М
М
17:44
Математические байки
И обратите внимание, числители продолжают быть вполне хорошо записывающимися!
Victor Kleptsyn
М
17:44
Математические байки
А вот соответствующее место у Ламберта —
Victor Kleptsyn
М
17:45
Математические байки
(Он не делит на степени переменной — у него это v — и чуть по-другому работает со знаками)
Victor Kleptsyn
М
17:48
Математические байки
Значение в нуле у f_3 равно
(2*4)/5! = 1/(3*5),
значит, на следующем шаге мы рассмотрим разность
f_2 - 5 f_3,
и опять поделим её на (-x^2), чтобы получить f_4, и так далее.
(2*4)/5! = 1/(3*5),
значит, на следующем шаге мы рассмотрим разность
f_2 - 5 f_3,
и опять поделим её на (-x^2), чтобы получить f_4, и так далее.
Victor Kleptsyn
М
17:51
Математические байки
Давайте я напишу ещё f_4 — а потом посмотрим на них повнимательнее:
Victor Kleptsyn
М
М
17:54
Математические байки
Попробуем придумать, а как бы такие произведения чётных чисел в числителях могли получаться. Вообще, умножение на степень переменной отвечает дифференцированию. Но несколько применений такой операции оставили бы произведение чисел — а у нас произведение только чётных. Значит, нужно нечётные степени "пропускать", уменьшая степень переменной после дифференцирования ещё на 1.
Victor Kleptsyn
М
17:55
Математические байки
Так рассмотрим оператор D= -(1/x) d/dx:
Victor Kleptsyn
М
М
17:56
Математические байки
Тогда f_1 это в точности D(f_0). А f_2 это D(f_1). И вообще
f_k= D^k f_0 (!)
f_k= D^k f_0 (!)
Victor Kleptsyn
М
17:56
Математические байки
Ответ уже красивый — но осталось понять, как это доказать.
Victor Kleptsyn
М
18:05
Математические байки
Заметим, что f_1 = sin(x)/x = D[cos x] = Df_0 просто по определению. И если посмотреть на D^2 f_0, то мы так же по определению получаем
Victor Kleptsyn
М
М
18:05
Математические байки
Так что на начальном этапе всё сходится.
Victor Kleptsyn
М
18:06
Математические байки
Но на это можно посмотреть как на дифференциальное уравнение на f_0=cos x — необычное, потому что в терминах D, а не обычной производной:
Victor Kleptsyn
М
М
18:10
Математические байки
Применим теперь к нему D. В правой части, конечно, останется ноль; в левой D[f_0] это f_1, D[-Df_0]=-D[f_1], а вот при применении к произведению x^2 D^2[f_0] срабатывает правило Лейбница: производная может упасть на первый сомножитель, а может на второй. Слагаемое от второго это просто x^2 D^3[f_0]=x^2 D^2[f_1], а вот при применении D к первому сомножителю получится -2 D^2[f_0]=-2 D[f_1], в дополнение к уже имеющемуся -D[f_1]. Итого —
Victor Kleptsyn
М
М
18:11
Математические байки
Значит, второе неполное частное равно 3, а f_3=D^2[f_1]. И продолжая по индукции, получаем
Victor Kleptsyn
М
М
18:12
Математические байки
(Каждое применение D увеличивает коэффициент в середине на 2).
Victor Kleptsyn
М
18:13
Математические байки
Вот мы и получили, что все наши "остатки" это f_k=D^k[f_0], а неполные частные это нечётные числа (2k+1).
(Конечно, можно было работать и по индукции из явных разложений в ряд Тейлора, но мне кажется, так получается красивее.)
(Конечно, можно было работать и по индукции из явных разложений в ряд Тейлора, но мне кажется, так получается красивее.)
Victor Kleptsyn
М
18:16
Математические байки
In reply to this message
И мы получили обещанное разложение тангенса в цепную дробь — по крайней мере, на уровне формальных рядов. Собственно, я подозреваю, что этого хватит и для того, чтобы доказать настоящую сходимость (потому что мы знаем, как устроены результаты последовательных вычитаний, совсем явно!), но мне кажется, техничность этого уже будет заметно превышать уровень "рассказываемой байки".
Victor Kleptsyn
М
18:26
Математические байки
In reply to this message
Ну и — даже если за формулами в канале следить не очень просто, мне хочется сказать, что всё последнее рассуждение это не "магия".
Как только мы поставили себе цель "разложить тангенс в цепную дробь" — ну, и угадали, что лучше работать не алгоритмом Евклида для tg x и 1, а для sin x и cos x, дальше мы не могли не преуспеть. Мы обязаны были (если не делать арифметических ошибок) получить те ряды, которые получили — и даже если не угадать, что они получаются с помощью дифференциального оператора -(1/x) d/dx, можно было просто по индукции доказать, что они всегда и впрямь такие.
Как только мы поставили себе цель "разложить тангенс в цепную дробь" — ну, и угадали, что лучше работать не алгоритмом Евклида для tg x и 1, а для sin x и cos x, дальше мы не могли не преуспеть. Мы обязаны были (если не делать арифметических ошибок) получить те ряды, которые получили — и даже если не угадать, что они получаются с помощью дифференциального оператора -(1/x) d/dx, можно было просто по индукции доказать, что они всегда и впрямь такие.
Victor Kleptsyn
М
18:28
Математические байки
Ну и, кажется, на этом рассказ об иррациональности пи можно закончить — доказательство и впрямь завершено.
Victor Kleptsyn
19 March 2020
М
12:28
Математические байки
Ещё пара слов в дополнение ко вчерашнему. Во-первых — цитата из книги Фердинанда Рудио.
"О квадратурѣ круга", вышедшей в 1911 году в Одессе:
"О квадратурѣ круга", вышедшей в 1911 году в Одессе:
Victor Kleptsyn
М
12:28
Математические байки
А вся книга выложена тут — https://www.mathesis.ru/book/rudio/
Victor Kleptsyn
М
12:29
Математические байки
Во-вторых, по соседству с цепными дробями есть история про последовательности (или ряды) Фарея.
Victor Kleptsyn
М
12:30
Математические байки
Давайте возьмём все несократимые дроби p/q на отрезке [0,1], у которых знаменатель q не превосходит некоторого фиксированного числа N. И упорядочим их по возрастанию.
Victor Kleptsyn
М
12:30
Математические байки
Определение. То, что получилось, называется последовательностью Фарея порядка N.
Victor Kleptsyn
М
12:32
Математические байки
А как понять, куда какие дроби будут попадать при увеличении N?
Victor Kleptsyn
М
12:33
Математические байки
При переходе от N=3 к N=4 всё просто —
Victor Kleptsyn
М
М
12:34
Математические байки
К N=5 — уже чуть менее, но всё ещё легко:
Victor Kleptsyn
М
М
12:34
Математические байки
А вот расставить все дроби со знаменателем 7 может оказаться не очень тривиально:
Victor Kleptsyn
М
М
12:35
Математические байки
Вопрос: а как понять (не выполняя кучи сравнений), что куда ставить?
Victor Kleptsyn
М
12:36
Математические байки
Второй вопрос — а как устроены расстояния между соседними дробями в последовательности Фарея?
Victor Kleptsyn
М
12:44
Математические байки
In reply to this message
Скажем, в примере выше:
5/7 приходит между 2/3 и 3/4,
4/7 — между 1/2 и 3/5.
5/7 приходит между 2/3 и 3/4,
4/7 — между 1/2 и 3/5.
Victor Kleptsyn
М
14:06
Математические байки
И уже несложно угадать, что 5/7 это (2+3)/(3+4), а 4/7 это (1+3)/(2+5).
Victor Kleptsyn
М
14:06
Математические байки
То есть — новая дробь это всегда "сумма двоечника своих соседей", числитель с числителем, знаменатель со знаменателем.
Victor Kleptsyn
М
14:10
Математические байки
Такую "сумму" называют медиантой; то, что она заключена между этими дробями, можно увидеть по-всякому, но лучше всего опять переходом от "проективной" картины к линейной. А именно — сопоставим каждой дроби p/q точку (p,q) плоскости; тогда взятие медианты это просто сложение векторов:
Victor Kleptsyn
М
14:13
Математические байки
А разность двух соседних дробей a/b и c/b в любой последовательности Фарея — это 1/(bd). Что, опять-таки, можно угадать, посмотрев на несколько примеров; скажем,
3/5-4/7=(21-20)/35,
2/3-3/5=(10-9)/15;
после пары-тройки таких вычитаний становится понятно, что в числителе должны всегда быть единицы...
3/5-4/7=(21-20)/35,
2/3-3/5=(10-9)/15;
после пары-тройки таких вычитаний становится понятно, что в числителе должны всегда быть единицы...
Victor Kleptsyn
М
14:45
Математические байки
In reply to this message
И, конечно, это означает, что площадь соответствующих параллелограмов равна 1. И если поверить в предыдущий факт — что новоприходящая дробь это всегда медианта соседей — то это мгновенно доказывается по индукции. Ведь каждый из двух новопоявляющихся параллелограммов имеет такую же площадь:
Victor Kleptsyn
М
14:47
Математические байки
Собственно, вывод в другую сторону (что до медианты, с меньшим, чем b+d, знаменаетелем, ничего не появится) тоже мгновенный. Потому что если между a/b и c/d появляется e/f, то разности:
e/f-a/b не меньше 1/bf
c/d-e/f не меньше 1/df,
а в сумме не меньше
1/bf + 1/df = (b+d)/bdf.
e/f-a/b не меньше 1/bf
c/d-e/f не меньше 1/df,
а в сумме не меньше
1/bf + 1/df = (b+d)/bdf.
Victor Kleptsyn
М
14:48
Математические байки
Поскольку мы делили отрезок длины 1/bd — то f не меньше, чем b+d.
Victor Kleptsyn
М
14:49
Математические байки
На самом деле, сумма двух выводов выше доказывает по индукции и то, и другое, но в этом проще убедиться самостоятельно.
С другой стороны — то, что в числителе разности всегда 1, можно увидеть из формулы Пика.
С другой стороны — то, что в числителе разности всегда 1, можно увидеть из формулы Пика.
Victor Kleptsyn
М
14:51
Математические байки
Ибо у треугольника с вершинами O=(0,0), A=(a,b), B=(c,d) других целых точек нет ни внутри (иначе бы a/b и c/d не были соседними в последовательности Фарея), ни на границе (по той же причине для стороны AB и потому что дроби несократимы для сторон OA и OB). А по формуле Пика его площадь — которая есть половина площади соответствующего параллелограмма — тогда равна
3/2 - 1 = 1/2.
3/2 - 1 = 1/2.
Victor Kleptsyn
М
14:55
Математические байки
Отсюда же, кстати, следует и теорема Дирихле о приближении — что для любого N любое вещественное число x можно приблизить дробью p/q, со знаменателем q, не большим N, так, чтобы
|x-p/q| < 1/Nq.
|x-p/q| < 1/Nq.
Victor Kleptsyn
М
14:59
Математические байки
Действительно, пусть x на отрезке [0,1] (добавить целое число уж точно можно); рассмотрим последовательность Фарея порядка N и тот отрезок
c/d < x < a/b,
куда наше приближаемое число попало. Раз медианта e/f=(a+c)/(b+d) уже не вошла в последовательность Фарея, то у неё слишком большой знаменатель f=b+d>N. Подотрезки, на которые она делит наш отрезок, имеют длину 1/bf (со второй вершиной a/b) и 1/df (со второй вершиной c/d).
Соответственно, берём тот из них, куда попала наша точка x, и берём вторую вершину в качестве приближения. Победа!
c/d < x < a/b,
куда наше приближаемое число попало. Раз медианта e/f=(a+c)/(b+d) уже не вошла в последовательность Фарея, то у неё слишком большой знаменатель f=b+d>N. Подотрезки, на которые она делит наш отрезок, имеют длину 1/bf (со второй вершиной a/b) и 1/df (со второй вершиной c/d).
Соответственно, берём тот из них, куда попала наша точка x, и берём вторую вершину в качестве приближения. Победа!
Victor Kleptsyn
М
15:01
Математические байки
Конечно же, эту теорему можно доказать и без этой науки, с помощью принципа Дирихле, рассмотрев точки 0,x,2x,...,Nx на окружности R/Z длины 1; две их них ближе, чем 1/N — а тогда их разность ближе, чем 1/N, к 0 на окружности R/Z, то есть |qx-p|<1/N для некоторого целого p.
Victor Kleptsyn
М
15:04
Математические байки
In reply to this message
(И конечно же, подходящие дроби появляются среди тех, которые будут ближайшими к x сверху и снизу в последовательностях Фарея разного порядка — а многогратная замена одной из них на медианту с другой это и есть описанный у Арнольда "алгоритм вытягивания носов".)
Victor Kleptsyn
М
15:11
Математические байки
In reply to this message
А последнее, что я тут хотел упомянуть — это кусочек истории. Фарей был английским геологом, и опубликовал это свойство таких последовательностей без доказательства в 1816 году в Philosophical Magazine —
Victor Kleptsyn
М
М
15:22
Математические байки
Это письмо попало на глаза Коши, который обрадовался, немедленно всё доказал, и назвал такие последовательности дробей последовательностями Фарея.
Но ещё в 1802 году, за 14 лет до того, в Journal de l'École Polytechnique появилась статья Charles Haros:
Но ещё в 1802 году, за 14 лет до того, в Journal de l'École Polytechnique появилась статья Charles Haros:
Victor Kleptsyn
М
15:23
Математические байки
Каковой Haros, увы, остался незаслуженно забыт.
Victor Kleptsyn
М
15:24
Математические байки
Два связанных исторических вопроса, которые я люблю задавать, когда рассказываю про работу Haros:
1) Что стоит перед фамилией Haros?
2) Какой год стоит на титульном листе журнала, опубликованного в 1802 году?
1) Что стоит перед фамилией Haros?
2) Какой год стоит на титульном листе журнала, опубликованного в 1802 году?
Victor Kleptsyn
М
15:31
Математические байки
Конечно же, ответ на второй вопрос не мог бы быть 1802 или 1801 или 1803 — было бы неинтересно. :)
Но если вспомнить, что в это время во Франции происходило —
Но если вспомнить, что в это время во Франции происходило —
Victor Kleptsyn
М
15:32
Математические байки
Отпечатано в месяце мессидоре года десятого!
Victor Kleptsyn
М
15:32
Математические байки
Ну и ответ на первый — стоит там C.-en, то есть Citoyen, гражданин:
Victor Kleptsyn
М
М
15:34
Математические байки
А по соседству с его статьёй опубликован отзыв (правда, странный) на будущую знаменитую Disquisitiones arithmeticae некоего господина Гаусса из Брунсвика.
Victor Kleptsyn
М
15:35
Математические байки
(M = Monsieur = господин)
Victor Kleptsyn
М
15:39
Математические байки
Да, совсем в заключение — ещё пара картинок из (мне кажется, очень стоящей того) книги Аллена Хатчера "Topology of Numbers", https://pi.math.cornell.edu/~hatcher/TN/TNbook.pdf .
Если распространить построение дробей медиантами на всю [проективную] прямую — начиная с нуля 0/1 и с бесконечности 1/0, сделать стереографическую проекцию и соединить дугами дроби, которые хоть в какой-то момент окажутся соседними —
Если распространить построение дробей медиантами на всю [проективную] прямую — начиная с нуля 0/1 и с бесконечности 1/0, сделать стереографическую проекцию и соединить дугами дроби, которые хоть в какой-то момент окажутся соседними —
Victor Kleptsyn
М
15:39
Математические байки
— то получается вот такая красивая картина:
Victor Kleptsyn
М
15:41
Математические байки
Ну и совсем в заключение — оказывается, в терминах распределения последовательностей Фарея можно эквивалентно переформулировать гипотезу Римана. Но это уже точно тема для другого рассказа...
Victor Kleptsyn
М
15:44
Математические байки
Последнее — вчера объявили лауреатов премии Абеля этого года: ими стали Г. Фюрстенберг и Г. А. Маргулис.
Victor Kleptsyn
М
15:44
Математические байки
Н
Непрерывное математическое образование 18.03.2020 15:01:09
https://www.abelprize.no/nyheter/vis.html?tid=76103
Сегодня объявлены лауреаты премии Абеля 2020 года: Гилель Фюрстенберг (Hebrew University of Jerusalem, Israel) и Григорий Александрович Маргулис (Yale University, New Haven, CT, USA)
“for pioneering the use of methods from probability and dynamics in group theory, number theory and combinatorics”
Сегодня объявлены лауреаты премии Абеля 2020 года: Гилель Фюрстенберг (Hebrew University of Jerusalem, Israel) и Григорий Александрович Маргулис (Yale University, New Haven, CT, USA)
“for pioneering the use of methods from probability and dynamics in group theory, number theory and combinatorics”
Victor Kleptsyn
М
15:45
Математические байки
Про работы Маргулиса, боюсь, я сходу не готов рассказывать, но вот про (по крайней мере, какие-то) работы Фюрстенберга — это просто план на следующий рассказ :)
Victor Kleptsyn
20 March 2020
М
13:49
Математические байки
Итак, обещанное про работы Фюрстенберга. Их много и разных; начать я хочу, пожалуй, не с основного его направления — зато с очень красивой работы про доказательство теоремы Семереди методами эргодической теории.
Victor Kleptsyn
М
13:49
Математические байки
Для начала — что такое теорема Семереди?
Есть классическая теорема Ван дер Вардена. Которая утверждает, что если натуральные числа раскрашены в конечное число цветов, то найдутся сколь угодно длинные арифметические прогрессии одного цвета.
Есть классическая теорема Ван дер Вардена. Которая утверждает, что если натуральные числа раскрашены в конечное число цветов, то найдутся сколь угодно длинные арифметические прогрессии одного цвета.
Victor Kleptsyn
М
13:50
Математические байки
Кстати — то же правда и в больших размерностях: если точки решётки L — например, множества Z^2 челочисленных точек плоскости — раскрашены в конечное число цветов, и есть конечное подмножество F в L ("шаблон"), то найдётся гомотетичное F одноцветное подмножество L. Об этом можно почитать в дубнинской брошюре В.О. Бугаенко, "Обобщённая теорема Ван дер Вардена" (см. https://www.mccme.ru/free-books/dubna/bugaenko.pdf ) — но это не основная тема моего рассказа, так что я вернусь на прямую.
Victor Kleptsyn
М
13:51
Математические байки
Так вот: мы знаем, что при раскраске N в конечное число цветов найдутся сколь угодно длинные одноцветные арифметические прогрессии. Но раз число цветов конечно, значит, есть один конкретный цвет, в котором есть сколь угодно длинные прогрессии. А нельзя ли как-нибудь его "указать"?
Victor Kleptsyn
М
13:52
Математические байки
Оказывается, можно, и (на уровне формулировки!) очень просто. А именно — давайте определим верхнюю плотность подмножества A в N как верхний предел при n, стремящемся к бесконечности, того, какую долю составляют элементы A среди {1,...,n}.
Victor Kleptsyn
М
М
13:52
Математические байки
Легко увидеть, что если натуральные числа разбиты на конечное число подмножеств, то сумма их верхних плотностей не меньше 1 — в частности, у хотя бы одного из них верхняя плотность больше нуля.
Victor Kleptsyn
М
14:01
Математические байки
Так вот, гипотеза Эрдеша и Турана 1936 года утверждала, что во всяком подмножестве N положительной верхней плотности есть сколь угодно длинные арифметические прогрессии. (Да, забыл сказать: теорема Ван дер Вардена это 1927 год).
Victor Kleptsyn
М
14:02
Математические байки
В 1953 году Roth доказал, что в множестве положительной верхней плотности найдутся прогрессии длины 3; в 1969-м — Семереди доказал это для прогрессий длины 4. И только в 1975-м тот же Семереди доказал эту гипотезу для прогрессий произвольной длины — с тех пор это утверждение называется теоремой Семереди.
Victor Kleptsyn
М
14:09
Математические байки
Так вот — всего лишь двумя годами позднее, в 1977 году, появилось доказательство Фюрстенберга теоремы Семереди методами эргодической теории. Но — опять-таки, прежде, чем я перейду к собственно этому доказательству, мне ещё хочется сказать пару слов про "соседние" утверждения.
Victor Kleptsyn
М
14:11
Математические байки
Есть более сильная гипотеза Эрдеша: пусть подмножество A таково, что ряд из обратных к его элементам расходится. Тогда в A есть сколь угодно длинные арифметические прогрессии.
Victor Kleptsyn
21 March 2020
М
18:46
Математические байки
In reply to this message
Продолжим?
Сразу видно, что эта гипотеза Эрдеша это более сильное утверждение: несложно проверить, что если верхняя плотность A положительна, то сумма ряда (1/n) по n из A расходится.
Сразу видно, что эта гипотеза Эрдеша это более сильное утверждение: несложно проверить, что если верхняя плотность A положительна, то сумма ряда (1/n) по n из A расходится.
Victor Kleptsyn
М
18:51
Математические байки
И — известно, что ряд из обратных простых 1/p тоже расходится. Это можно увидеть разными способами, правильнее всего, наверно, это увидеть через тождество Эйлера для дзета-функции:
Victor Kleptsyn
М
М
18:51
Математические байки
При s=1 в левой части стоит (расходящийся) гармонический ряд, значит, сумма логарифмов сомножителей правой части расходится. А
-ln(1-1/p)~ 1/p.
-ln(1-1/p)~ 1/p.
Victor Kleptsyn
М
18:52
Математические байки
Конечно, можно сослаться и на асимптотический закон распределения простых чисел, что p_n ~ n ln n, а ряд 1/(n ln n) расходится, но мне это показалось неправильным — ибо если посмотреть, сколько всего внутри асимптотического закона закопано, чтобы его вывести...
Victor Kleptsyn
М
18:52
Математические байки
Так вот — сумма ряда из обратных простых расходится. Поэтому следствием из гипотезы Эрдеша было бы то, что есть сколь угодно длинные прогрессии, состоящие из простых чисел.
Victor Kleptsyn
М
18:53
Математические байки
И это и правда так — утверждающая это теорема Грина-Тао была доказана ими в 2004 году (и это был один из результатов, принесших Тао премию Филдса).
Victor Kleptsyn
М
18:54
Математические байки
Но что же до самой гипотезы Эрдеша про множества с расходящейся суммой обратных, то в общем виде она остаётся недоказанной — более того, не доказано даже, что в таком множестве найдутся арифметические прогрессии длины 3 !
Victor Kleptsyn
М
19:02
Математические байки
Вот препринт 2014 года (и статья 2016го) — https://arxiv.org/abs/1405.5800 — где говорится, сколько может быть чисел на отрезке от 1 до N, так, чтобы среди них не было трёх последовательных членов арифметической прогрессии. Но оценка там совершенно не мешает расходимости ряда из обратных...
(См. также — https://en.wikipedia.org/wiki/Erd%C5%91s_conjecture_on_arithmetic_progressions )
(См. также — https://en.wikipedia.org/wiki/Erd%C5%91s_conjecture_on_arithmetic_progressions )
Victor Kleptsyn
М
19:31
Математические байки
In reply to this message
Возвращаясь к доказательству Фюрстенберга теоремы Семереди. Удивительным образом, предложенное им доказательство такого "комбинаторного" факта работает на языке динамических систем.
Victor Kleptsyn
М
19:36
Математические байки
Вообще, динамическая система [с дискретным временем] — это пара из множества состояний X и (обычно — непрерывного) отображения f:X->X.
Грубо говоря — отображение говорит, "в каком состоянии окажется система через секунду".
Грубо говоря — отображение говорит, "в каком состоянии окажется система через секунду".
Victor Kleptsyn
М
19:38
Математические байки
При этом, если мы говорим о физических системах — например, о качающемся маятнике, или о планете, движущейся по орбите — то состояние это не только положение, но и скорость. А отображение f — это решение задающего эволюцию системы дифференциального уравнения: "где и с какой скоростью мы окажется через заданный промежуток времени".
Victor Kleptsyn
М
19:59
Математические байки
И при изучении теории динамических систем не начинают с чего-нибудь жутко сложного вроде всей Солнечной системы — а с модельных примеров. И один из таких (очень важных, и потом играющих во всей науке) примеров это "символическая динамика": X это множество всех последовательностей из 0 и 1, а f:X->X это "левый сдвиг" — первый элемент выбрасывается, все остальные сдвигаются на один влево.
Victor Kleptsyn
М
20:02
Математические байки
Кстати — модельный пример хаотической динамики это "отображение удвоения" на окружности:
f: \varphi -> 2\varphi.
Одна его итерация удваивает расстояние между близкими точками — так что, если исходная точка известна лишь приближённо, через очень небольшое число итераций f о её образе уже ничего нельзя сказать ("нельзя предсказать погоду через месяц").
f: \varphi -> 2\varphi.
Одна его итерация удваивает расстояние между близкими точками — так что, если исходная точка известна лишь приближённо, через очень небольшое число итераций f о её образе уже ничего нельзя сказать ("нельзя предсказать погоду через месяц").
Victor Kleptsyn
М
20:03
Математические байки
Так вот — если мы возьмём окружность длины 1 (а не 2π) и рассмотрим последовательность цифр после запятой в двоичной записи \varphi — то к этой последовательности как раз таки применяется левый сдвиг!
Victor Kleptsyn
М
20:08
Математические байки
Более того, это я, конечно, отклоняюсь в сторону, но символическую динамику можно "пристегнуть" (пусть и разрывным образом, что не всегда хорошо) к любой динамической системе. Выберем любое подмножество A в X.
И сопоставим любой начальной точке x её судьбу — последовательность 0 и 1, говорящую, правда ли, что
f^k(x) принадлежит A.
Тогда судьба f(x) — это просто левый сдвиг судьбы x.
И сопоставим любой начальной точке x её судьбу — последовательность 0 и 1, говорящую, правда ли, что
f^k(x) принадлежит A.
Тогда судьба f(x) — это просто левый сдвиг судьбы x.
Victor Kleptsyn
М
20:09
Математические байки
In reply to this message
Ну и мы, на самом деле, уже видели пример такого, когда брали поворот окружности на золотое сечение — и в качестве судьбы получали слово Фибоначчи.
Victor Kleptsyn
М
20:12
Математические байки
Но давайте вернёмся к теореме Семереди. Для её динамического доказательства Фюрстенберг перевёл её на язык динамических систем — а именно, как раз таки символической динамики.
А именно — начальное множество A это подмножество натуральных чисел. Так превратим его в его характеристическую функцию x_A — в последовательность 0 и 1, говорящих, принадлежит ли A данное натуральное число.
А именно — начальное множество A это подмножество натуральных чисел. Так превратим его в его характеристическую функцию x_A — в последовательность 0 и 1, говорящих, принадлежит ли A данное натуральное число.
Victor Kleptsyn
М
20:13
Математические байки
И давайте рассмотрим множество C ("цилиндр") последовательностей, у которых первый элемент это 1.
Victor Kleptsyn
М
20:17
Математические байки
На множестве последовательностей действует отображение f — левый сдвиг. На этом языке
Victor Kleptsyn
М
М
20:17
Математические байки
(где x_A — это та последовательность 0 и 1, которая кодирует A)
Victor Kleptsyn
М
20:19
Математические байки
Поэтому условие на верхнюю плотность — это условие на то, сколь часто итерации x_A возвращаются в C:
Victor Kleptsyn
М
М
20:32
Математические байки
Но и условие на арифметическую прогрессию среди элементов A тоже проговаривается в динамических терминах. Например, если мы хотим, чтобы m+d, m+2d, m+3d все принадлежали A, то нужно, чтобы образы точки
f^{m-1}(x_A) за d, 2d и за 3d итераций одновременно принадлежали C. Или, иными словами, если мы возьмём декартово произведение XxXxX и на нём будем применять покомпонетно f, f^2 и f^3,
f^{m-1}(x_A) за d, 2d и за 3d итераций одновременно принадлежали C. Или, иными словами, если мы возьмём декартово произведение XxXxX и на нём будем применять покомпонетно f, f^2 и f^3,
Victor Kleptsyn
М
М
20:34
Математические байки
то точка (w,w,w), где w=f^{m-1}(x_A), должна за d итераций вернуться в CxCxC.
Victor Kleptsyn
М
20:37
Математические байки
Но если говорить о возвращении, то в теории динамических систем есть теорема Пуанкаре о возвращении. Пусть отображение f сохраняет некоторую меру µ. Например, представим себе, что мы наблюдаем установившееся течение несжимаемой жидкости. Тогда, если мы выделим какое-то множество B положительной меры, µ(B)>0, то µ-почти все точки рано или поздно в него вернутся.
Victor Kleptsyn
М
20:46
Математические байки
Давайте я для простоты предположу, что динамическая система обратимая — наше отображение f, вообще-то, таковым не является (оно забывает первый символ), но мы можем рассмотреть и двусторонне-бесконечные последовательности с точно таким же отображением левого сдвига — сдвигающим всю последовательность на один индекс влево.
Victor Kleptsyn
М
20:49
Математические байки
Так вот — давайте сначала увидим, что хоть одна точка B в него вернётся. Действительно, если это не так, то у нас будут образы B, f(B), f^2(B), все друг с другом не пересекающиеся. И у каждого будет одна и та же мера µ(B). Но на них на всех тогда не хватит места — мера µ(X) конечна (кажется, я не написал этого явно — но обычно в динамических системах меры берут вероятностными, т.е. µ(X)=1).
Victor Kleptsyn
М
20:53
Математические байки
Ну и если бы мера подмножества B' тех точек, которые никогда не вернутся в B, была бы положительна — мы бы взяли B' вместо B (если точка никогда не возвращается в B, то и в его подмножество B' она никогда не вернётся), и повторили бы предыдущее рассуждение.
Victor Kleptsyn
М
21:35
Математические байки
Так вот — буквально сослаться на теорему Пуанкаре о возвращении нельзя, и нам придётся всё-таки работать с исходной системой, а не с заманчиво-изящным декартовым произведением. А то, что нужно применить, называется Furstenberg multiple recurrence theorem (и собственно, в его динамическом доказательстве и скрыта вся сложность; так-то эта теорема оказывается просто эквивалентна теореме Семереди).
Но — я надеюсь, что какие-то стыкующиеся кусочки динамического взгляда в этой задаче уже проглядывают...
Но — я надеюсь, что какие-то стыкующиеся кусочки динамического взгляда в этой задаче уже проглядывают...
Victor Kleptsyn
М
21:36
Математические байки
И пара цитат в заключение — одна из самого Фюрстенберга, из той самой его работы 1977 года —
Victor Kleptsyn
М
21:37
Математические байки
И вторая — со страницы 28 работы Эрдеша, "On the combinatorial problems which I would most like to see solved" —
Victor Kleptsyn
М
21:41
Математические байки
Ну и на этом я на сегодня хочу прекратить дозволенные речи.
Victor Kleptsyn
22 March 2020
М
19:53
Математические байки
По-моему, это прекрасно:
Victor Kleptsyn
М
23 March 2020
М
20:19
Математические байки
Давайте я соберу идеи доказательства Фюрстенберга теоремы Семереди в более строгий рассказ. Итак, пусть у нас есть множество A натуральных чисел положительной верхней плотности.
Victor Kleptsyn
М
20:20
Математические байки
Рассмотрим множество X двусторонних последовательностей нулей и единиц — иными словами, отображений из Z в {0,1}.
На X есть (взаимно-однозначное) отображение f левого сдвига — сдвигающее всю последовательность на один символ влево. Есть подмножество E — состоящее из последовательностей, у которых на нулевом месте стоит 1. И есть последовательность x_A — характеристическая (или индикаторная) функция A.
На X есть (взаимно-однозначное) отображение f левого сдвига — сдвигающее всю последовательность на один символ влево. Есть подмножество E — состоящее из последовательностей, у которых на нулевом месте стоит 1. И есть последовательность x_A — характеристическая (или индикаторная) функция A.
Victor Kleptsyn
М
20:21
Математические байки
Ингредиент, про который я в прошлый раз не очень подробно сказал, откуда он берётся, это инвариантная мера µ (вероятностная — то есть с µ(X)=1; вообще, в теории динсистем обычно меры вероятностные).
Victor Kleptsyn
М
20:21
Математические байки
Есть такая теорема Крылова-Боголюбова: для любого непрерывного отображения f метрического компакта X в себя есть (хоть какая-то!) f-инвариантная мера.
Victor Kleptsyn
М
20:22
Математические байки
И доказывается она (почти) явной конструкцией — которая называется процедурой Крылова-Боголюбова. А именно: возьмём любую начальную точку x_0 — и посмотрим на её орбиту x_n:=f^n(x_0).
Возьмём начальный отрезок этой орбиты длины n — и распределим по нему равномерно единичную массу:
(1/n) в точку x_0
(1/n) в точку x_1=f(x_0)
...
(1/n) в точку x_{n-1}.
Получающаяся мера µ_n ( =распределение единичной массы) не инвариантна: применение f переведёт её в чуть-чуть от неё отличающуюся (добавится (1/n) в точке x_n и пропадёт в точке x_0).
Возьмём начальный отрезок этой орбиты длины n — и распределим по нему равномерно единичную массу:
(1/n) в точку x_0
(1/n) в точку x_1=f(x_0)
...
(1/n) в точку x_{n-1}.
Получающаяся мера µ_n ( =распределение единичной массы) не инвариантна: применение f переведёт её в чуть-чуть от неё отличающуюся (добавится (1/n) в точке x_n и пропадёт в точке x_0).
Victor Kleptsyn
М
20:23
Математические байки
Но чем больше n — тем мера ближе к инвариантной. И поэтому любая предельная точка последовательности мер µ_n — это уже в точности инвариантная мера. А пространство вероятностных мер на компакте — само по себе компакт (относительно *-слабой сходимости мер, если говорить совсем аккуратно). Поэтому из последовательности µ_n можно выделить сходящуюся подпоследовательность µ_{n_j} — предел которой и будет искомой инвариантной мерой.
Victor Kleptsyn
М
20:25
Математические байки
Так вот: запустим процедуру Крылова-Боголюбова для нашего отображения и для начальной точки x_A. При этом число n принадлежит A тогда и только тогда, когда на нулевом месте у f^n(x_A) стоит 1 — то есть f^n(x_A) лежит в E.
Victor Kleptsyn
М
20:26
Математические байки
Поэтому мера µ_n(E) это доля элементов A среди отрезка 0,1,...,n-1. И по определению верхней плотности есть подпоследовательность моментов n_m, для которой µ_{n_m}(E) стремится к rho(A)>0.
Выделив сходящуюся подпоследовательность µ_{n_{m_j}} уже из µ_{n_m} — получим меру µ, которая и инвариантная, и такова, что µ(E)=\rho(A)>0.
Выделив сходящуюся подпоследовательность µ_{n_{m_j}} уже из µ_{n_m} — получим меру µ, которая и инвариантная, и такова, что µ(E)=\rho(A)>0.
Victor Kleptsyn
М
20:27
Математические байки
После чего остаётся применить самый сложный шаг доказательства — теорему Фюрстенберга о кратном возвращении (Furstenberg Multiple Recurrence Theorem); я её процитирую по статье И.Д. Шкредова "Теорема Семереди и задачи об арифметических прогрессиях" (http://www.mi-ras.ru/~ishkredov/Paperru/12.pdf )
Victor Kleptsyn
М
20:28
Математические байки
Итак — для некоторого d мера µ множества
Victor Kleptsyn
М
М
20:28
Математические байки
положительна. Но это множество это последовательности, у которых на местах 0, d,...,(k-1)d стоят единицы.
Victor Kleptsyn
М
20:28
Математические байки
In reply to this message
А если вспомнить, как мы меру µ строили — усредняя сдвиги — то отсюда следует, что для того же d верхняя плотность тех m, для которых точки m, m+d,...,m+(k-1)d принадлежат A, положительна. В частности, такие прогрессии любой длины k есть.
Victor Kleptsyn
М
20:36
Математические байки
Тот переход, что мы сейчас выполнили, называется принципом соответствия Фюрстенберга; опять-таки, я процитирую статью Шкредова:
Victor Kleptsyn
М
20:37
Математические байки
На самом деле, теорема Фюрстенберга о кратном возвращении теореме Семереди даже и эквивалентна (см. второе предложение выше). Но самый технически сложный шаг работы Фюрстенберга (и о чём я пока не сказал ни слова) — это как теорему о кратном возвращении динамическими методами доказывать. И там начинают возникать слова "слабое перемешивание", "компактный фактор", и ещё разные — но вот туда я как раз не пойду.
Victor Kleptsyn
М
20:37
Математические байки
У этой науки есть ещё обобщения — многомерная теорема Фюрстенберга и Кацнельсона и следующая из неё многомерная версия теоремы Семереди ; см. https://terrytao.wordpress.com/2008/02/10/254a-lecture-10-the-furstenberg-correspondence-principle/ —
Victor Kleptsyn
М
20:38
Математические байки
То есть в подмножестве Z^m с положительной верхней плотностью есть подмножества, гомотетичные любому конечному "шаблону" (v_1,...,v_k).
Victor Kleptsyn
М
20:39
Математические байки
Но, наверное, в этом месте я хочу закончить рассказ об этой работе Фюрстенберга — и продолжить рассказ о других его работах в следующий раз.
Victor Kleptsyn
24 March 2020
М
15:25
Математические байки
===
В качестве паузы (чтобы писать не только о динамических системах) — короткий рассказ про совсем другое: про числа Каталана.
Допустим, нас интересует, сколькими способами можно расставить n открывающих и n закрывающих скобок так, чтобы в любом начальном подслове закрывающих скобок было не больше, чем открывающих. То есть (), (()), ()() можно, ())( или ())(()() нельзя.
Если нарисовать "по точкам" график разности "число открывающих скобок минус число закрывающих из первых k символов", то он состоит из отрезков, идущих под 45 градусов либо вправо-вверх, либо вправо-вниз. Соответственно, число Каталана это число таких путей, идущих из точки (0,0) в точку (2n,0) и не спускающихся ниже оси абсцисс по пути.
Оно же равно количеству деревьев на плоскости с n+1 вершиной, отмеченным корнем и "землёй" (или, равносильно, первым ребром из этой вершины): если обходить это дерево "снаружи", начиная с первого ребра — расстояние до корня как раз и будет меняться на +1/-1 на каждом шаге:
В качестве паузы (чтобы писать не только о динамических системах) — короткий рассказ про совсем другое: про числа Каталана.
Допустим, нас интересует, сколькими способами можно расставить n открывающих и n закрывающих скобок так, чтобы в любом начальном подслове закрывающих скобок было не больше, чем открывающих. То есть (), (()), ()() можно, ())( или ())(()() нельзя.
Если нарисовать "по точкам" график разности "число открывающих скобок минус число закрывающих из первых k символов", то он состоит из отрезков, идущих под 45 градусов либо вправо-вверх, либо вправо-вниз. Соответственно, число Каталана это число таких путей, идущих из точки (0,0) в точку (2n,0) и не спускающихся ниже оси абсцисс по пути.
Оно же равно количеству деревьев на плоскости с n+1 вершиной, отмеченным корнем и "землёй" (или, равносильно, первым ребром из этой вершины): если обходить это дерево "снаружи", начиная с первого ребра — расстояние до корня как раз и будет меняться на +1/-1 на каждом шаге:
Victor Kleptsyn
М
М
15:27
Математические байки
Оно же число триангуляций [диагоналями] n+2-угольника. Ну и вообще у чисел Каталана очень много разных определений и свойств — но речь не об этом, а о том, как их посчитать.
Victor Kleptsyn
М
15:27
Математические байки
Во-первых, можно через производящие функции. Несложно увидеть рекуррентное соотношение для чисел Каталана C_n:
Victor Kleptsyn
М
М
15:28
Математические байки
Если собрать их в производящую функцию,
F(z)=\sum_n C_n z^n,
то в правой части рекуррентного соотношения стоят коэффициенты F(z)^2 — которые ещё нужно сдвинуть на одну степень. Поэтому оно превращается в квадратное уравнение на производящую функцию:
F(z)-1=z F^2(z).
F(z)=\sum_n C_n z^n,
то в правой части рекуррентного соотношения стоят коэффициенты F(z)^2 — которые ещё нужно сдвинуть на одну степень. Поэтому оно превращается в квадратное уравнение на производящую функцию:
F(z)-1=z F^2(z).
Victor Kleptsyn
М
15:29
Математические байки
Отсюда находим F(z) —
Victor Kleptsyn
М
М
15:30
Математические байки
(знак в числителе должен быть минусом, потому что иначе числитель не обратится в ноль при z=0, а у нас не может быть особенности вида 1/z).
Victor Kleptsyn
М
15:30
Математические байки
И, наконец, разложив (1-4z)^{1/2} по биному Ньютона для нецелой степени — где нецелый биномиальный коэффициент определяется как
Victor Kleptsyn
М
М
15:31
Математические байки
(конечно же, бином Ньютона для нецелой степени это то же самое, что и ряд Тейлора) — и немного переписав получившееся произведение (1/2)*(1/2)*(3/2)*(5/2)*...*4^n/n!, получаем явный ответ
Victor Kleptsyn
М
М
15:39
Математические байки
И это, конечно, очень техничный способ получить ответ. Но мне больше всего нравится другой способ — который я узнал из лекции А. А. Кириллова на "Студенческих чтениях НМУ" (предшественник семинара "Глобус").
Victor Kleptsyn
М
15:43
Математические байки
Давайте находить сразу для всех точек (n,k) число способов добраться до них ломаными (с шагами (1,1) и (1,-1)), не спускаясь ниже оси абсцисс. Только развернём картинку на 90 градусов по часовой стрелке — чтобы ломаные шли вниз-вправо или вниз-влево.
Victor Kleptsyn
М
15:44
Математические байки
Получается вот такая картинка —
Victor Kleptsyn
М
15:46
Математические байки
Верхняя 1 это точка старта, (0,0); до каждой точки можно дойти из той, которая выше-левее или выше-правее, поэтому число способов складывается. Наконец, на один ряд левее её идёт запрещённая вертикаль — в этих точках мы нарушили запрет "ниже нуля не спускаться", поэтому там по определению стоят [красные] нули.
Victor Kleptsyn
М
15:48
Математические байки
То есть — правило как у треугольника Паскаля, только вот красные нули "прибиты гвоздями по определению".
Victor Kleptsyn
М
15:55
Математические байки
In reply to this message
Прошу прощения — не заметил опечатку в картинке выше: в последней строчке должно быть, конечно,
5 9 5 1
Вот правильная картинка —
5 9 5 1
Вот правильная картинка —
Victor Kleptsyn
М
15:58
Математические байки
In reply to this message
Так вот — а нельзя ли нам эти нули как-нибудь тоже включить в правило треугольника Паскаля?
Оказывается, что можно. Давайте заменим их на зеркало — а за зеркалом пусть будет антимир: такие же числа, но с минусами.
Оказывается, что можно. Давайте заменим их на зеркало — а за зеркалом пусть будет антимир: такие же числа, но с минусами.
Victor Kleptsyn
М
16:01
Математические байки
Теперь правило треугольника Паскаля (каждое число равно сумме двух расположенных над ним) выполнено слева от вертикали нулей, выполнено справа от вертикали нулей (потому что зеркальный образ), и выполнено на самой этой вертикали, потому что мы складываем отличающиеся знаком числа.
Victor Kleptsyn
М
16:04
Математические байки
Поэтому вся эта картинка строится просто по тому же правилу, что и обычный треугольник Паскаля, но из первой строчки "(-1) 1".
Victor Kleptsyn
М
16:06
Математические байки
Но поскольку правило линейное — то она будет разностью обычных треугольников Паскаля, растущего из правой 1 и из левой (-1).
Victor Kleptsyn
М
16:08
Математические байки
В частности, n-е число Каталана равно:
Victor Kleptsyn
М
М
16:28
Математические байки
Ну и вообще, если нам нужно расставить k символов "+1" и m-k символов "-1" — так, чтобы ни на каком начальном участке сумма не была бы отрицательной — то количество способов это сделать будет равно
Victor Kleptsyn
М
М
16:32
Математические байки
Из этой же картины/интерпретации можно получить и ответ на связанный вопрос из теории вероятностей/случайных блужданий. Допустим, у Васи есть один рубль, и он играет в орлянку — каждый раз ставя по рублю и с равной вероятностью выигрывая и проигрывая. Если в какой-то момент денег у него не остаётся — то он уходит. С какой вероятностью за n шагов он не разорится?
Victor Kleptsyn
М
16:40
Математические байки
In reply to this message
Понятно, что если умножить эту вероятность на 2^n, то получится число путей, делающих n шагов и не пересекающих запретную "линию нулей" — но приходящих куда угодно. И это сумма элементов (справа от линии нулей) в соответствующей строке нашего треугольника.
Victor Kleptsyn
М
16:45
Математические байки
Но эта сумма телескопическая — это сумма разностей биномиальных коэффициентов, и каждый коэффициент, кроме первого, в ней сокращается. А именно — там будет
Victor Kleptsyn
М
М
16:45
Математические байки
— где k это n/2 при чётном n и (n+1)/2 при нечётном. То есть эта сумма, это просто центральный биномиальный коэффициент.
Victor Kleptsyn
М
16:49
Математические байки
На самом деле, это несложно превратить и в биективное соответствие между путями из (0,1) длины n, не касающимися оси абсцисс, и всеми путями из (0,1) в (n,a), где a=1 или 2 в зависимости от чётности n (наименьшая возможная сумма у Васи).
Victor Kleptsyn
М
16:51
Математические байки
А именно — берём такой путь. Если он уже нигде не касается оси абсцисс, то оставляем. Если где-нибудь касается, то берём первый момент разорения, и отражаем путь относительно оси абсцисс на участке до этого момента (а потом не меняем).
Victor Kleptsyn
М
16:55
Математические байки
Получаем путь из точки (0,-1). Сдвигаем его на 2 вверх, получаем опять путь из (0,1). После чего повторяем процедуру — если разорения нет, оставляем, если есть, отражаем на участке "до разорения включительно" и сдвигаем на 2 вверх.
Victor Kleptsyn
М
16:57
Математические байки
Насколько я понимаю, такое и аналогичные рассуждения в теории вероятностей/случайных блужданиях называются "методом отражения".
Victor Kleptsyn
М
17:05
Математические байки
Ну и в заключение — вот ссылка на "Студенческие чтения НМУ", где опубликована лекция Кириллова —
https://www.mccme.ru/free-books/globus/iumlectures1.pdf , и соответствующий скриншот:
https://www.mccme.ru/free-books/globus/iumlectures1.pdf , и соответствующий скриншот:
Victor Kleptsyn
М
17:07
Математические байки
И — что "Студенческие чтения", что выпуски "Глобуса" я очень советую. Собственно, вот оглавление первого выпуска "Глобуса", https://www.mccme.ru/free-books/globus/globus1.pdf —
Victor Kleptsyn
25 March 2020
М
17:31
Математические байки
(Рассказывает Евгений Смирнов.)
Victor Kleptsyn
М
17:31
Математические байки
Н
Непрерывное математическое образование 25.03.2020 17:29:29
если кто хочет послушать лекцию НМУ по комбинаторике (пути и определители, формула Макмагона и проч.) — zoom.us/j/981375600 (начало через пару минут)
Victor Kleptsyn
М
18:12
Математические байки
(Ключевой момент — подсчёт пар непересекающихся путей)
Victor Kleptsyn
26 March 2020
М
17:44
Математические байки
Присоединяюсь — это должно быть интересно.
Victor Kleptsyn
М
17:44
Математические байки
q
qtasep 26.03.2020 17:32:37
А вот кому онлайн-семинар по теории вероятностей: https://www.wim.uni-mannheim.de/doering/one-world/ (встречи каждый четверг, докладчики все замечательные).
Через полчаса (в 6 вечера по Москве) доклад Nathanael Berestycki (Vienna) - Random walks on random planar maps and Liouville Brownian motion - про асимптотику случайных графов и квантовую гравитацию
Зум: https://zoom.us/j/997986033
Через полчаса (в 6 вечера по Москве) доклад Nathanael Berestycki (Vienna) - Random walks on random planar maps and Liouville Brownian motion - про асимптотику случайных графов и квантовую гравитацию
Зум: https://zoom.us/j/997986033
Victor Kleptsyn
М
17:50
Математические байки
Я подозреваю, что вот эта иллюстрация Николя Курьяна (Nicolas Curien) весьма в тему того доклада, который начнётся через 10 минут:
Victor Kleptsyn
М
17:53
Математические байки
(Это "случайным образом собранная сфера"; интересно, что такая сфера — с той метрикой на ней, которая получается — имеет хаусдорфову размерность 4, а вовсе не 2.)
Victor Kleptsyn
5 April 2020
М
19:09
Математические байки
Давайте я продолжу "абелевский сезон" — и в этот раз расскажу про два результата Маргулиса.
Victor Kleptsyn
М
19:12
Математические байки
Я начну со случайной теоремы Минковского — которую уже упоминал qtasep:
Victor Kleptsyn
М
19:12
Математические байки
q
qtasep 20.03.2020 04:47:59
Я был на одном докладе Маргулиса, на конференции 50-летия ИППИ летом 2011 года (в коем ИППИ и я, и Маргулис до сих пор формально числимся). Эта конференция довольно важная для меня, т.к. сразу после нее я переехал в Штаты на постдок.
Ну так вот, Маргулис там прочитал доклад про относительно просто формулируемый, но очень красивый результат про случайную теорему Минковского. Конечно, это не главный его результат - про более важные вещи есть книги и доступные обзоры на них (https://www.ams.org/journals/bull/2005-42-02/S0273-0979-05-01051-7/S0273-0979-05-01051-7.pdf, https://www.ams.org/journals/bull/1992-27-01/S0273-0979-1992-00306-3/S0273-0979-1992-00306-3.pdf)
Неслучайная теорема Минковского формулируется так. Пусть есть выпуклое центрально симметричное множество A в R^n, объема больше 2^n. Тогда для любой унимодулярной решетки (в частности, для стандартной решетки Z^n), A содержит ненулевой элемент этой решетки.
Случайность позволяет ослабить предположения о симметричности и выпуклости A. Пусть A - произвольное множество положительного объема. Возьмем случайную решетку по мере Хаара на SL(n,R) / SL(n,Z). Тогда вероятность того, что случайная решетка не пересекает A, оценивается сверху как C(n)/m(A), где m(A) - объем множества A, а константа C(n) зависит от размерности.
В частности, если объем A стремится к бесконечности, то A пересекает почти все решетки, независимо от предположений симметричности и выпуклости.
Интересно, что доказательство для в размерности 2 наиболее сложное, и требует теории автоморфных форм.
Вот так и получаются очень красивые результаты, если добавить немного вероятности к известным 100 лет классическим теоремам.
Ну так вот, Маргулис там прочитал доклад про относительно просто формулируемый, но очень красивый результат про случайную теорему Минковского. Конечно, это не главный его результат - про более важные вещи есть книги и доступные обзоры на них (https://www.ams.org/journals/bull/2005-42-02/S0273-0979-05-01051-7/S0273-0979-05-01051-7.pdf, https://www.ams.org/journals/bull/1992-27-01/S0273-0979-1992-00306-3/S0273-0979-1992-00306-3.pdf)
Неслучайная теорема Минковского формулируется так. Пусть есть выпуклое центрально симметричное множество A в R^n, объема больше 2^n. Тогда для любой унимодулярной решетки (в частности, для стандартной решетки Z^n), A содержит ненулевой элемент этой решетки.
Случайность позволяет ослабить предположения о симметричности и выпуклости A. Пусть A - произвольное множество положительного объема. Возьмем случайную решетку по мере Хаара на SL(n,R) / SL(n,Z). Тогда вероятность того, что случайная решетка не пересекает A, оценивается сверху как C(n)/m(A), где m(A) - объем множества A, а константа C(n) зависит от размерности.
В частности, если объем A стремится к бесконечности, то A пересекает почти все решетки, независимо от предположений симметричности и выпуклости.
Интересно, что доказательство для в размерности 2 наиболее сложное, и требует теории автоморфных форм.
Вот так и получаются очень красивые результаты, если добавить немного вероятности к известным 100 лет классическим теоремам.
Victor Kleptsyn
М
19:15
Математические байки
Собственно, из формулировок тут уже всё сказано — но давайте я скажу пару слов более подробно про доказательства.
Давайте начнём с классической теоремы Минковского. Вот пусть у нас есть выпуклое, симметричное относительно начала координат тело в R^n. Утверждается, что максимальный объём, который может у такого тела быть, чтобы оно не содержало внутри ни одной другой точки Z^n — это 2^n, объём куба [-1,1]^n.
Давайте начнём с классической теоремы Минковского. Вот пусть у нас есть выпуклое, симметричное относительно начала координат тело в R^n. Утверждается, что максимальный объём, который может у такого тела быть, чтобы оно не содержало внутри ни одной другой точки Z^n — это 2^n, объём куба [-1,1]^n.
Victor Kleptsyn
М
19:21
Математические байки
И доказательство очень простое и изящное: давайте сожмём наше тело в 2 раза, а потом отправим R^n в тор
T^n = R^n / Z^n.
Если объём тела был больше 2^n, то после сжатия он больше 1 — то есть больше объёма тора. Значит, какие-то две точки сжатого тела, P/2 и Q/2, перейдут в одну. То есть они отличаются на вектор из Z^n.
T^n = R^n / Z^n.
Если объём тела был больше 2^n, то после сжатия он больше 1 — то есть больше объёма тора. Значит, какие-то две точки сжатого тела, P/2 и Q/2, перейдут в одну. То есть они отличаются на вектор из Z^n.
Victor Kleptsyn
М
19:22
Математические байки
Но
P/2 - Q/2 = (P+(-Q))/2,
а точка (-Q) тоже принадлежит нашему телу из-за его симметричности. Ну а полусумма точек принадлежит телу по выпуклости. Вот мы и нашли целую точку внутри тела.
P/2 - Q/2 = (P+(-Q))/2,
а точка (-Q) тоже принадлежит нашему телу из-за его симметричности. Ну а полусумма точек принадлежит телу по выпуклости. Вот мы и нашли целую точку внутри тела.
Victor Kleptsyn
М
19:29
Математические байки
То же самое верно и для любой другой решётки в R^n, лишь бы у неё фундаментальный параллелепипед (из которого тор в факторе получается склейкой противоположных граней) был бы единичного объёма.
(А если не единичного, то тело должно быть объёма >2^n раз больше. Но нас будут интересовать только решётки, у которых этот объём равен 1 — их называют унимодулярными ; в конце концов, любая другая такой гомотетична.)
(А если не единичного, то тело должно быть объёма >2^n раз больше. Но нас будут интересовать только решётки, у которых этот объём равен 1 — их называют унимодулярными ; в конце концов, любая другая такой гомотетична.)
Victor Kleptsyn
М
19:31
Математические байки
Но понятно, что ни от условия симметричности относительно нуля, ни от условия выпуклости, в общем случае отказаться нельзя. Потому что в первом случае можно взять прямоугольник
[0.1,0.9]x[0,10000]
на плоскости, а во втором — просто и цинично вырезать из круга радиуса 1000 окрестности всех целых точек.
[0.1,0.9]x[0,10000]
на плоскости, а во втором — просто и цинично вырезать из круга радиуса 1000 окрестности всех целых точек.
Victor Kleptsyn
М
19:36
Математические байки
Вопрос, который рассматривается в случайной версии теоремы Минковского, такой: а что, если мы выбираем решётку в R^n случайным образом? Можно ли так выбрать множество A большой меры Лебега, чтобы его избегало "много" (или хотя бы "заметная доля") решёток?
Victor Kleptsyn
М
19:38
Математические байки
Ответ: нельзя. Вероятность того, что случайная унимодулярная решётка не пересекает A, не превосходит C_n/m(A), где C_n — константа (зависящая только от размерности n), а m(A) — мера A. В частности, (любое!) множество бесконечной меры Лебега пересекают почти все решётки.
Victor Kleptsyn
М
19:40
Математические байки
И давайте я об этом чуть-чуть поговорю (собственно, ссылка на текст Маргулиса — http://mi.mathnet.ru/ppi2063 ).
Victor Kleptsyn
М
19:48
Математические байки
Во-первых, как устроен выбор случайной решётки?
Саму решётку можно задать, как M(Z^n), где M — линейное отображение с определителем 1 (потому что решётка унимодулярная), то есть элемент SL(n,R). Но отображение M можно выбрать многими способами (это выбор базиса решётки) — замена M на MB, где B из SL(n,Z), ничего не меняет. Поэтому решётка — это всё равно, что элемент SL(n,R)/SL(n,Z).
Саму решётку можно задать, как M(Z^n), где M — линейное отображение с определителем 1 (потому что решётка унимодулярная), то есть элемент SL(n,R). Но отображение M можно выбрать многими способами (это выбор базиса решётки) — замена M на MB, где B из SL(n,Z), ничего не меняет. Поэтому решётка — это всё равно, что элемент SL(n,R)/SL(n,Z).
Victor Kleptsyn
М
19:48
Математические байки
(Фактор тут это, конечно, не факторгруппа, а однородное пространство — множество классов смежности)
Victor Kleptsyn
М
20:10
Математические байки
На SL(n,R) есть хорошая — сохраняемая умножением как справа, так и слева — мера Хаара.
Есть два способа её построить — более техничный это сказать, что SL(n,R) это группа Ли, то есть и группа, и многообразие. Взять любую форму объёма на касательном пространстве в единице группы — и умножением слева принести во все остальные точки группы. Так получается левоинвариантная мера Хаара. После чего надо будет убедиться, что она (для случая SL(n,R)) и правоинвариантна.
Более простой способ — посмотрим на SL(n,R) как на гиперповерхность в матрицах nxn,
Mat(n)=R^(n^2).
Группа SL(n,R) действует на Mat(n) умножением как слева, так и справа, и оба умножения сохраняют n^2-мерную меру Лебега (потому что одно умножением работает по отдельности со столбцами, а другое со строками). А теперь уроним меру с Mat(n) на гиперповерхность SL(n,R) "коническим образом": скажем, что мера подмножества SL(n,R) это мера опирающегося на него конуса (из начала координат).
Есть два способа её построить — более техничный это сказать, что SL(n,R) это группа Ли, то есть и группа, и многообразие. Взять любую форму объёма на касательном пространстве в единице группы — и умножением слева принести во все остальные точки группы. Так получается левоинвариантная мера Хаара. После чего надо будет убедиться, что она (для случая SL(n,R)) и правоинвариантна.
Более простой способ — посмотрим на SL(n,R) как на гиперповерхность в матрицах nxn,
Mat(n)=R^(n^2).
Группа SL(n,R) действует на Mat(n) умножением как слева, так и справа, и оба умножения сохраняют n^2-мерную меру Лебега (потому что одно умножением работает по отдельности со столбцами, а другое со строками). А теперь уроним меру с Mat(n) на гиперповерхность SL(n,R) "коническим образом": скажем, что мера подмножества SL(n,R) это мера опирающегося на него конуса (из начала координат).
Victor Kleptsyn
М
20:11
Математические байки
Раз эта мера инвариантна относительно умножений справа — её можно "уронить" на фактор SL(n,R)/SL(n,Z), точно так же, как можно уронить меру Лебега на R^n на тор-фактор R^n/Z^n.
Victor Kleptsyn
М
20:13
Математические байки
Причём, раз она инвариантна относительно умножений справа — получающаяся мера на решётках будет сохраняться, если мы к R^n применим любое SL(n,R)-преобразование.
Victor Kleptsyn
М
20:20
Математические байки
Неочевидное утверждение — что объём фактора (т. е. пространства решёток) будет конечным. Проблема в том, что пространство унимодулярных решёток некомпактно — можно взять последовательность решёток, получающуюся из Z^n умножением первой координаты на r и второй на 1/r — тогда при r->0 эти решётки никуда сходиться не будут.
Но тем не менее, объём фактора действительно конечен.
Но тем не менее, объём фактора действительно конечен.
Victor Kleptsyn
М
20:31
Математические байки
А раз объём фактора конечен — можно на него поделить, и получится вероятностная мера на множестве решёток. И в этом смысле мы и выбираем случайную решётку.
Вот, теорема сформулирована!
Вот, теорема сформулирована!
Victor Kleptsyn
М
20:44
Математические байки
Давайте теперь посмотрим на её доказательство (и я тут следую http://mi.mathnet.ru/ppi2063 — хотя собираюсь чуть-чуть "срезать углы" и очень надеюсь, что при этом не навру).
Victor Kleptsyn
М
20:44
Математические байки
Начнём со случая размерности как минимум 3.
Victor Kleptsyn
М
20:52
Математические байки
Пусть у нас есть какая-то "хорошая" функция f на R^n — например, характеристическая функция I_A нашего множества А. Ей можно сопоставить функцию \hat{f} на пространстве решёток: сумму значений f по всем ненулевым точкам решётки.
Victor Kleptsyn
М
20:53
Математические байки
В частности, если мы берём f=I_A — то
\hat{f}(L) это число ненулевых точек решётки L, попавших в A.
\hat{f}(L) это число ненулевых точек решётки L, попавших в A.
Victor Kleptsyn
М
21:24
Математические байки
Так вот, первый шаг доказательства — это лемма, что матожидание \hat{f} (по мере Хаара на множестве решёток) равно интегралу от f (по мере Лебега m на R^n). И это очень естественно.
Во-первых, можно переставить два интеграла — и увидеть, что матожидание \hat{f} должно быть равно интегралу от f(x) с каким-то множителем, зависящим от x — или, что то же самое, по какой-то мере µ на R^n.
Но во-вторых, мы знаем, что распределение на решётках в R^n инвариантно относительно действия SL(n,R). А значит, должна быть инвариантна и мера µ. Но тогда µ это мера Лебега, быть может, умноженная на какую-то константу. Остаётся проверить, что эта константа равна 1.
Действительно: давайте посмотрим на шар B очень большого радиуса R. Для него большинство решёток в нём выбивает как раз примерно m(B) точек. И если поверить, что вклад "совсем кривых" решёток в матожидание маленький — то вот мы и получаем, что константа должна быть равна 1.
Во-первых, можно переставить два интеграла — и увидеть, что матожидание \hat{f} должно быть равно интегралу от f(x) с каким-то множителем, зависящим от x — или, что то же самое, по какой-то мере µ на R^n.
Но во-вторых, мы знаем, что распределение на решётках в R^n инвариантно относительно действия SL(n,R). А значит, должна быть инвариантна и мера µ. Но тогда µ это мера Лебега, быть может, умноженная на какую-то константу. Остаётся проверить, что эта константа равна 1.
Действительно: давайте посмотрим на шар B очень большого радиуса R. Для него большинство решёток в нём выбивает как раз примерно m(B) точек. И если поверить, что вклад "совсем кривых" решёток в матожидание маленький — то вот мы и получаем, что константа должна быть равна 1.
Victor Kleptsyn
М
21:32
Математические байки
Из статьи Маргулиса —
Victor Kleptsyn
М
21:41
Математические байки
Второй (и, видимо, в этом месте главный технический) шаг — это оценка на L_2-норму \hat{I_A}. А именно, оказывается (и это совершенно не очевидно), что для любого множества A интеграл от квадрата от \hat{I_A} оказывается не больше, чем если заменить I_A на шар B той же меры Лебега:
Victor Kleptsyn
М
22:05
Математические байки
Наконец, посмотрим на \hat{I_A} и на \hat{I_B} как на случайные величины.
Victor Kleptsyn
М
22:08
Математические байки
У них одинаковые матожидания — равные m(A). При этом дисперсия Dξ равна
Dξ = E(ξ^2) - (Eξ)^2,
и из неравенства выше следует, что дисперсия для \hat{I_A} не больше, чем для \hat{I_B}.
Dξ = E(ξ^2) - (Eξ)^2,
и из неравенства выше следует, что дисперсия для \hat{I_A} не больше, чем для \hat{I_B}.
Victor Kleptsyn
М
22:21
Математические байки
Наконец, мы уже видели, что даже для шара B — для которого, вообще-то, дисперсия максимальна, — случайная величина \hat{I_B} очень похожа на постоянную a:=m(A). Собственно, явная выкладка показывает, что дисперсия \hat{I_B} равна C_n*a:
Victor Kleptsyn
М
М
22:41
Математические байки
А значит, вероятность, что \hat{I_B} на случайной решётке L равна нулю — то есть что решётка L не пересекает A (нигде, кроме, быть может, нуля) — можно оценить по неравенству Чебышева: она не превышает
D(\hat{I_A})/a^2 = C_n a / a^2 = C_n/a = m(A).
Вот и всё!
D(\hat{I_A})/a^2 = C_n a / a^2 = C_n/a = m(A).
Вот и всё!
Victor Kleptsyn
М
22:43
Математические байки
Осталось посмотреть, что же происходит в размерности 2 (в частности, почему буквально предыдущее рассуждение применить нельзя) — но это я, наверное, дорасскажу уже завтра.
Victor Kleptsyn
6 April 2020
М
20:13
Математические байки
Продолжим?
Я обещал рассказать, в чём проблема в размерности 2. Для начала посмотрим, какова мера решёток, в которых кратчайший вектор имеет длину r. Я хочу сказать, что когда r маленькое, эта мера ведёт себя как константа*r^2.
Я обещал рассказать, в чём проблема в размерности 2. Для начала посмотрим, какова мера решёток, в которых кратчайший вектор имеет длину r. Я хочу сказать, что когда r маленькое, эта мера ведёт себя как константа*r^2.
Victor Kleptsyn
М
20:15
Математические байки
In reply to this message
Мы знаем, что матожидание числа векторов, попадающих в диск радиуса r, равно πr^2. Ибо это как раз мера этого диска.
Victor Kleptsyn
М
20:18
Математические байки
Дальше нужно учесть, что если кратчайший вектор v решётки имеет длину меньше r/2, то в диск попадут не только v и -v, но и 2v и -2v, и вообще потребуется некоторая аккуратная работа. Тем не менее — давайте я сейчас ей пренебрегу и предположу, что всё равно мы получим cr^2 для такой асимптотики.
Victor Kleptsyn
М
20:20
Математические байки
In reply to this message
Проблема, которая у нас возникнет — это что преобразования \hat{I_A} хоть всё ещё и интегрируемы — но уже не интегрируемы в квадрате. И происходит это как раз рядом с такими "вырожденными" решётками (у которых один базисный вектор очень короткий, а другой очень длинный).
Victor Kleptsyn
М
20:23
Математические байки
Действительно, пусть, например, A это диск единичного радиуса. Тогда на решётках, у которых кратчайший вектор v имеет длину r, преобразование \hat{I_A} равно 2*[1/r], потому что в A попадают v, 2v, ..., [1/r]*v, и ещё все те же вектора с минусами.
Victor Kleptsyn
М
20:23
Математические байки
И мы оказываемся в ситуации, как если бы мы на плоскости в окрестности нуля работали с функцией [1/r]: она интегрируема, но вот её квадрат — уже нет.
Victor Kleptsyn
М
20:23
Математические байки
Собственно, цитируя Маргулиса —
Victor Kleptsyn
М
М
20:25
Математические байки
А идея тут такая: нам нужно было какое-нибудь подходящее преобразование. Если у "вырожденных" решёток начинает возникать проблема из-за того, что сразу много пропорциональных друг другу векторов попадает в A и мы вынуждены их все считать — так давайте их не считать!
Victor Kleptsyn
М
20:26
Математические байки
Давайте вместо преобразования \hat{f}, где мы складываем значения f во всех ненулевых точках решётки, рассмотрим преобразование Tf, где мы рассмотрим сумму только по примитивным (неделимым) векторам:
Victor Kleptsyn
М
20:32
Математические байки
Тогда из тех же соображений, что и раньше, матожидание Tf (как случайной величины — то есть вычисляемой на случайной решётке) должно быть константой на интеграл f по R^n по мере Лебега.
Victor Kleptsyn
М
20:34
Математические байки
Ну и эту константу легко найти из тех же соображений, что и раньше — взяв в качестве f индикатор круга большого радиуса R. Но теперь (для большинства решёток) туда попадает не столько вершин, какова его площадь, а в \zeta(2) раз меньше. Ведь " шанс, что два больших случайных числа взаимно просты, равен 1/zeta(2) ".
Victor Kleptsyn
М
20:37
Математические байки
In reply to this message
Маргулис в этом месте заменяет меру на пространстве решёток, умножая её на \zeta(2), чтобы сохранилось красивое тождество с равенством интегралов — но мне приятнее оставить меру вероятностной и поделить на \zeta(2) интеграл f.
Victor Kleptsyn
М
21:18
Математические байки
Так вот — благодаря такой замене, новое преобразование T(I_A) уже не убегает на бесконечность даже на решётках с очень короткими векторами. А последние шаги доказательства оказываются очень похожими. Во-первых, если взять диск B площади, равной мере нашего множества A, то случайная величина T(I_B) — тоже почти константа (что мы, собственно, уже видели выше).
Victor Kleptsyn
М
21:19
Математические байки
А во-вторых, оказывается, что T-образ функции с нулевым средним не увеличивает L_2-норму:
Victor Kleptsyn
М
21:29
Математические байки
И это и есть то самое место, где применяется теория автоморфных форм и вообще техника.
А дальше — если мы рассмотрим T-образ разницы I_A-I_B, то матожидание его квадрата не больше, чем 2a. И складывая это с оценкой на дисперсию T(I_B) — опять получаем линейную по a оценку на дисперсию
T(I_A)=T(I_A-I_B)+T(I_B).
Значит, T(I_A) опять обращается в 0 с вероятностью, не большей C/a. И значит, с вероятностью не больше C/m(A) случайная решётка не пересекает A.
А дальше — если мы рассмотрим T-образ разницы I_A-I_B, то матожидание его квадрата не больше, чем 2a. И складывая это с оценкой на дисперсию T(I_B) — опять получаем линейную по a оценку на дисперсию
T(I_A)=T(I_A-I_B)+T(I_B).
Значит, T(I_A) опять обращается в 0 с вероятностью, не большей C/a. И значит, с вероятностью не больше C/m(A) случайная решётка не пересекает A.
Victor Kleptsyn
М
21:31
Математические байки
Вот. Рассказ получился не самым простым — но и работа меньше, чем 15-летней давности!
Victor Kleptsyn
7 April 2020
М
14:58
Математические байки
Добрый день!
Я собираюсь продолжить рассказ про работы Маргулиса и геометрию решёток, но сначала — чтобы немного переключаться между сюжетами — вернёмся ненадолго к криптографии и к задаче факторизации.
Я собираюсь продолжить рассказ про работы Маргулиса и геометрию решёток, но сначала — чтобы немного переключаться между сюжетами — вернёмся ненадолго к криптографии и к задаче факторизации.
Victor Kleptsyn
М
14:59
Математические байки
In reply to this message
Мы уже видели метод Ленстры факторизации с помощью эллиптических кривых — который для больших чисел третий по эффективности. Удивительным образом, второй по эффективности метод, метод квадратичного решета, заметно проще и продвинутую науку не использует.
Victor Kleptsyn
М
15:00
Математические байки
А основан он на том, что если A^2=B^2 mod n, то либо A=B mod n, либо A=-B mod n, либо и (A+B), и (A-B) имеют нетривиальные общие делители с n. И если первый и второй варианты неинтересны, то последний как раз (алгоритмом Евклида) и приводит к факторизации.
Victor Kleptsyn
М
15:01
Математические байки
Остаётся такие нетривиальные пары (A,B) найти. Наверное, если бы мы искали B по данному A, то никакого выигрыша без факторизации мы бы не получили — кажется, задача просто равносильна факторизации.
Но можно искать именно пару — не зная, ни какое получится A, ни B.
Но можно искать именно пару — не зная, ни какое получится A, ни B.
Victor Kleptsyn
М
15:01
Математические байки
Итак, идея. Берём числа, примерно равные корню из n, и посмотрим на их квадраты по модулю n:
Victor Kleptsyn
М
М
15:02
Математические байки
Тогда, во-первых, любое a_k по модулю n является квадратом известного нам вычета (m+k).
Victor Kleptsyn
М
15:03
Математические байки
Но, во-вторых (и это ключевой шаг), можно попробовать найти произведение a_k, которое будет полным квадратом.
А именно — предположим, что у какой-то их части оказались одни и те же простые делители. Тогда, чтобы произведение каких-то a_{k_j} было полным квадратом, достаточно их перемножить так, чтобы все степени простых оказались чётными.
А именно — предположим, что у какой-то их части оказались одни и те же простые делители. Тогда, чтобы произведение каких-то a_{k_j} было полным квадратом, достаточно их перемножить так, чтобы все степени простых оказались чётными.
Victor Kleptsyn
М
15:04
Математические байки
Понятно, что если мы раскладываем на множители, скажем, 100-значное число n — то a_k будут порядка корня из n, то есть 50-значными. И раскладывать каждое из них на множители это опять та ещё задача.
Но — мы выберем некоторый набор Base "не слишком больших" простых (который называется базой ). Скажем — первую сотню тысяч, или миллион.
И если какое-то a_k не раскладывается в произведение простых из Base — то просто выбросим его. А если раскладывается — запомним (и назовём такое число " гладким ").
Но — мы выберем некоторый набор Base "не слишком больших" простых (который называется базой ). Скажем — первую сотню тысяч, или миллион.
И если какое-то a_k не раскладывается в произведение простых из Base — то просто выбросим его. А если раскладывается — запомним (и назовём такое число " гладким ").
Victor Kleptsyn
М
15:05
Математические байки
И когда мы, просто увеличивая k, наберём достаточно много гладких чисел (больше, чем простых в базе Base) — то вектора степеней разложения (координаты соответствуют простым из базы) начнут быть зависимыми по модулю 2. И произведение соответствующих a_{k_j} будет полным квадратом, и мы будем знать, чьим.
Victor Kleptsyn
М
15:06
Математические байки
Вот мы и получили совпадение: построенное произведение a_{k_j} будет и настоящим полным квадратом в обычных целых числах (так что A — обычный корень из этого произведения), и будет по модулю n сравнимо с квадратом произведения (m+k_j) — соответственно, B это произведение (m+k_j).
Victor Kleptsyn
М
15:07
Математические байки
Игрушечный пример: факторизуем число 64643.
Victor Kleptsyn
М
15:10
Математические байки
Оказывается, что взяв три небольших k=2,3,7, мы уже видим (mod 2)-линейную зависимость между векторами степеней:
Victor Kleptsyn
М
15:10
Математические байки
Находим A и B:
Victor Kleptsyn
М
15:10
Математические байки
И находим делители —
Victor Kleptsyn
М
15:17
Математические байки
Да, нам может не повезти. Никто не обещал, что первое же найденное соотношение окажется нетривиальным. Я бы (безответственно и навскидку) сказал, что шансы 50 на 50: можем найти нетривиальное соотношение, а можем тривиальное. Поэтому гладких чисел нужно находить не просто |Base|+1, а немного побольше (чтобы хоть одно соотношение да сработало)...
Victor Kleptsyn
М
15:21
Математические байки
Второе — что в базу можно брать не все простые, а только примерно половину. Потому что если простое число p делит a_k=(m+k)^2-n, то
n=(m+k)^2 mod p,
поэтому n является квадратичным вычетом по модулю p.
n=(m+k)^2 mod p,
поэтому n является квадратичным вычетом по модулю p.
Victor Kleptsyn
М
15:55
Математические байки
Ответ на вопрос "является ли n квадратичным вычетом по модулю p" называется символом Лежандра.
И его вполне можно быстро найти. Вручную я, скорее всего, воспользовался бы мультипликативностью и квадратичным законом взаимности. Но для программирования, пожалуй, проще всего сказать, что символ Лежандра a над p равен a^{(p-1)/2} (ибо малая теорема Ферма). А k-ю степень мы вычисляем за log(k) умножений, ибо череда возведений в квадраты.
И его вполне можно быстро найти. Вручную я, скорее всего, воспользовался бы мультипликативностью и квадратичным законом взаимности. Но для программирования, пожалуй, проще всего сказать, что символ Лежандра a над p равен a^{(p-1)/2} (ибо малая теорема Ферма). А k-ю степень мы вычисляем за log(k) умножений, ибо череда возведений в квадраты.
Victor Kleptsyn
М
15:56
Математические байки
Да, в качестве рекламы — про квадратичный закон взаимности (связывающий символы Лежандра p по модулю q и q по модулю p) мне очень нравится рассуждение отсюда — https://users.mccme.ru/smirnoff/papers/qrecip01.pdf
Victor Kleptsyn
М
16:00
Математические байки
In reply to this message
Но так или иначе, символ Лежандра быстро ищется — так что можно быстро понять, какие простые у нас не могут появиться в принципе. Собственно, именно поэтому повторение 2, 19, 37, 47 в примере выше не столь удивительно (хотя нам и повезло — уже три вектора в четырёхмерном пространстве оказались линейно зависимыми — но куча других простых в первых десятках тут не появилась вообще).
Victor Kleptsyn
М
16:09
Математические байки
Ну и последнее — это выбор размера базы. Возьмём слишком маленькую — и слишком мала будет доля гладких чисел, придётся перебирать много разных k. Скажем, много ли чисел вида
2^{p_1}*3^{p_2}*5^{p_3}
среди первого миллиона?
Возьмём слишком большую базу — и нужно будет много гладких чисел, опять-таки, придётся много перебирать.
2^{p_1}*3^{p_2}*5^{p_3}
среди первого миллиона?
Возьмём слишком большую базу — и нужно будет много гладких чисел, опять-таки, придётся много перебирать.
Victor Kleptsyn
М
16:22
Математические байки
Но на формулировке этой задачи оптимизации я, пожалуй, хочу в этом рассказе на сегодня остановиться.
Victor Kleptsyn
9 April 2020
М
13:22
Математические байки
Во-первых, моя работа над ошибками: то, что мы разобрали позавчера, это ещё не весь метод квадратичного решета, а его начальная часть. Её называют алгоритмом Диксона — обычно ссылаясь на его работу 1981 года (http://pages.cs.wisc.edu/~cs812-1/dixon.pdf ), где Диксон рассматривает квадраты случайно выбираемых чисел по модулю N и строго оценивает время работы такого алгоритма.
Victor Kleptsyn
М
13:23
Математические байки
Если же говорить более аккуратно о том, кто что придумал, то нужно сказать, что сам придумавший квадратичное решето Carl Pomerance в своей "Tale of two fractals" (https://www.ams.org/notices/199612/pomerance.pdf ) ссылается на Крайчика в 1920-е.
По соседству там был подход с получением небольших квадратов по модулю N через цепные дроби (с идеей, что для подходящих дробей P/Q к корню из N величины P^2-N Q^2 будут не очень большими), сначала в 1930-ых в работах Лемера и Пауэрса,
https://projecteuclid.org/download/pdf_1/euclid.bams/1183495051 , а потом в работах Morrison & Brillhart (https://www.ams.org/journals/mcom/1975-29-129/S0025-5718-1975-0371800-5/S0025-5718-1975-0371800-5.pdf ).
И давайте я тут дам слово Дональду Кнуту ("Искусство программирования", том 2, раздел 4.5.4):
По соседству там был подход с получением небольших квадратов по модулю N через цепные дроби (с идеей, что для подходящих дробей P/Q к корню из N величины P^2-N Q^2 будут не очень большими), сначала в 1930-ых в работах Лемера и Пауэрса,
https://projecteuclid.org/download/pdf_1/euclid.bams/1183495051 , а потом в работах Morrison & Brillhart (https://www.ams.org/journals/mcom/1975-29-129/S0025-5718-1975-0371800-5/S0025-5718-1975-0371800-5.pdf ).
И давайте я тут дам слово Дональду Кнуту ("Искусство программирования", том 2, раздел 4.5.4):
Victor Kleptsyn
М
14:06
Математические байки
In reply to this message
Во-вторых, давайте я сформулирую недостающую идею для квадратичного решета. Когда мы проверяем числа на гладкость — то есть на то, что они раскладываются на множители из выбранной базы — то наиболее прямолинейный подход состоит в том, чтобы пытаться на них на все разделить. И, конечно, в большинстве случаев впустую.
Представьте себе, что вы раскладываете на множители — и делите число M=1987645202877 на 197. Не делится. Переходите к 199. Опять не делится. Переходите дальше, и тут кто-то, пришедший понаблюдать за этим процессом, выдаёт — "а зачем вы делите на числа, на которые M не делится? Делить M надо на те числа, на которые делится!"
Скорее всего, вы захотите такому советчику много что сказать. Так вот, удивительная вещь состоит в том, что ровно так и работает квадратичное решето — за счёт того, что мы знаем, какие числа Q(x)=x^2-N на какие простые из базы будут делится!
Представьте себе, что вы раскладываете на множители — и делите число M=1987645202877 на 197. Не делится. Переходите к 199. Опять не делится. Переходите дальше, и тут кто-то, пришедший понаблюдать за этим процессом, выдаёт — "а зачем вы делите на числа, на которые M не делится? Делить M надо на те числа, на которые делится!"
Скорее всего, вы захотите такому советчику много что сказать. Так вот, удивительная вещь состоит в том, что ровно так и работает квадратичное решето — за счёт того, что мы знаем, какие числа Q(x)=x^2-N на какие простые из базы будут делится!
Victor Kleptsyn
М
14:29
Математические байки
А именно — вот у нас есть простое число p из базы. По модулю p наше N является квадратичным вычетом (иначе бы мы p из базы выкинули) — и мы можем (просто перебором, это всё равно не самая трудозатратная часть) найти корни a и (-a) из N. Но мы знаем, что Q(x) и Q(y) сравнимы, если x и y сравнимы по модулю p. Значит, на p будут делиться Q(x) при x вида a+n*p и (-a)+n*p, и только при таких!
То есть, к примеру, для простых порядка сотни тысяч или миллиона мы знаем, какие Q(x) нужно на них делить, и это должно дать ускорение в эту самую сотню тысяч-миллион раз.
То есть, к примеру, для простых порядка сотни тысяч или миллиона мы знаем, какие Q(x) нужно на них делить, и это должно дать ускорение в эту самую сотню тысяч-миллион раз.
Victor Kleptsyn
М
16:19
Математические байки
Так что глобальный алгоритм просеивания (действительно напоминающий решето Эратосфена) устроен следующим образом. Вот мы будем смотреть на числа вида
(m+k)^2-N,
где m это целая часть корня из N, а k пробегает какой-то интервал, и хотим из них отобрать гладкие.
Давайте считать произведение всех степеней простых из базы, на которые такие числа делятся. А именно — заведём массив W для логарифма такого произведения ("видишь длинное произведение — прологарифмируй!"); изначально заполним его нулями.
После чего для каждого p в цикле пробежим по k, для которых m+k имеют один из двух нужных остатков по модулю p, и добавим ln p к W[k]. И, конечно, это будет не цикл по k, а движение с шагом в p.
После чего обработаем делящиеся на p^2 числа (движение с шагом p^2, добавим ещё раз ln p), на p^3, и так далее.
В результате такого цикла мы для каждого k найдём, на какое максимальное гладкое число Q(m+k)=(m+k)^2-N делится. И, сравнив его с логарифмом Q(m+k), выясним, гладкое это число или нет.
И поскольку мы, вместо того, чтобы каждое число пытаться делить — добавляли ln p только туда, куда надо, алгоритм действительно очень сильно ускорился.
(m+k)^2-N,
где m это целая часть корня из N, а k пробегает какой-то интервал, и хотим из них отобрать гладкие.
Давайте считать произведение всех степеней простых из базы, на которые такие числа делятся. А именно — заведём массив W для логарифма такого произведения ("видишь длинное произведение — прологарифмируй!"); изначально заполним его нулями.
После чего для каждого p в цикле пробежим по k, для которых m+k имеют один из двух нужных остатков по модулю p, и добавим ln p к W[k]. И, конечно, это будет не цикл по k, а движение с шагом в p.
После чего обработаем делящиеся на p^2 числа (движение с шагом p^2, добавим ещё раз ln p), на p^3, и так далее.
В результате такого цикла мы для каждого k найдём, на какое максимальное гладкое число Q(m+k)=(m+k)^2-N делится. И, сравнив его с логарифмом Q(m+k), выясним, гладкое это число или нет.
И поскольку мы, вместо того, чтобы каждое число пытаться делить — добавляли ln p только туда, куда надо, алгоритм действительно очень сильно ускорился.
Victor Kleptsyn
М
16:27
Математические байки
Давайте я процитирую три абзаца из уже упомянутой "A Tale of Two Sieves" Карла Померанса:
Victor Kleptsyn
М
М
16:43
Математические байки
Кстати, зашифрованное в 1977 году создателями RSA сообщение "The Magic Words are Squeamish Ossifrage" (https://en.wikipedia.org/wiki/The_Magic_Words_are_Squeamish_Ossifrage ) было расшифровано как раз с использованием (чуть более продвинутой и приспособленной к распараллеливанию) версии квадратичного решета — позволившей разложить на множители соответствующее 129-значное число RSA-129 (см. https://en.wikipedia.org/wiki/RSA_numbers#RSA-129 )
Ну и на этом, наверное, я этот рассказ [на время?] завершу. Тут ещё осталось много чего нерасказанного (включая, например, распараллеливание вычислений), но вообще-то я собирался сделать всего лишь короткий перерыв между двумя рассказами о результатах Фюрстенберга и Маргулиса. :)
Ну и на этом, наверное, я этот рассказ [на время?] завершу. Тут ещё осталось много чего нерасказанного (включая, например, распараллеливание вычислений), но вообще-то я собирался сделать всего лишь короткий перерыв между двумя рассказами о результатах Фюрстенберга и Маргулиса. :)
Victor Kleptsyn
11 April 2020
М
18:10
Математические байки
Давайте я начну рассказывать об одном из результатов Маргулиса — о доказательстве гипотезы Оппенгейма (https://en.wikipedia.org/wiki/Oppenheim_conjecture ). И для начала посмотрим на саму эту гипотезу, посвящённую значениям квадратичной формы от нескольких переменных в целых точках.
Victor Kleptsyn
М
18:13
Математические байки
Вообще, значения квадратичной формы нескольких переменных в целых точках даже для квадратичной формы с целыми коэффициентами это большая, красивая и нетривиальная наука. Сразу можно вспомнить теорему Лагранжа, утверждающую, что любое натуральное число представляется как сумма четырёх квадратов. Иными словами, значения на Z^4 квадратичной формы B(x,y,z,t)=x^2+y^2+z^2+t^2
это все неотрицательные целые числа.
это все неотрицательные целые числа.
Victor Kleptsyn
М
18:16
Математические байки
Можно вспомнить критерий того, когда натуральное число n представляется как сумма двух квадратов: простые вида 4k+3 должны входить в разложение n на простые множители только в чётных степенях.
Victor Kleptsyn
М
18:23
Математические байки
Чуть менее известное, но тоже красивое утверждение — это в каких натуральных точках (x,y) квадратичная форма
B(x,y)=y^2 -xy - x^2
принимает значения плюс или минус 1. Оказывается, (x,y) должны быть тогда парой последовательных числами Фибоначчи — и это критерий. (Если мы разрешаем x и y быть отрицательными, то последовательность Фибоначчи тоже нужно будет продолжить на отрицательные индексы, и ещё разрешить одновременную смену их знака). Что, кстати, хорошее упражнение.
И отсюда идёт дорога к работам Матиясевича и решению 10-й проблемы Гильберта — но по этой дороге я сейчас не пойду. :)
B(x,y)=y^2 -xy - x^2
принимает значения плюс или минус 1. Оказывается, (x,y) должны быть тогда парой последовательных числами Фибоначчи — и это критерий. (Если мы разрешаем x и y быть отрицательными, то последовательность Фибоначчи тоже нужно будет продолжить на отрицательные индексы, и ещё разрешить одновременную смену их знака). Что, кстати, хорошее упражнение.
И отсюда идёт дорога к работам Матиясевича и решению 10-й проблемы Гильберта — но по этой дороге я сейчас не пойду. :)
Victor Kleptsyn
М
18:25
Математические байки
Так вот, возвращаясь к гипотезе — пусть у нас есть квадратичная форма (однородный многочлен степени два)
B(x_1,...,x_n)
в R^n. Рассмотрим множество X=B(Z^n) её значений во всевозможных целых точках. Вопрос, который нас будет интересовать — когда можно утверждать, что X всюду плотно?
B(x_1,...,x_n)
в R^n. Рассмотрим множество X=B(Z^n) её значений во всевозможных целых точках. Вопрос, который нас будет интересовать — когда можно утверждать, что X всюду плотно?
Victor Kleptsyn
М
18:26
Математические байки
Во-первых, нельзя, чтобы у формы B были бы целые коэффициенты. Или рациональные. Или одновременно пропорциональные рациональным. Так что будем рассматривать формы, которые не пропорциональны формам с целыми коэффициентами (и будем для краткости называть такие формы иррациональными ).
Victor Kleptsyn
М
18:27
Математические байки
Во-вторых, нельзя, чтобы форма B была знакоопределённой — если она положительно определена, то мы по определению не получим отрицательных значений, если отрицательно, положительных. Так что пусть она будет не-знакоопределённой [индефинитной].
Victor Kleptsyn
М
18:27
Математические байки
В-третьих, бессмысленно брать вырожденную форму — так что мы будем просить её невырожденности.
Достаточно ли попросить всего этого, чтобы X=B(Z^n) было всюду плотным? В размерности два — нет.
Достаточно ли попросить всего этого, чтобы X=B(Z^n) было всюду плотным? В размерности два — нет.
Victor Kleptsyn
М
18:31
Математические байки
И тут есть два естественных примера; и тут, и там мы будем смотреть на малые значения — принимает ли B на Z^2 малые ненулевые значения (ибо если множество значений плотно, то должна).
Пример 1. Давайте рассмотрим квадратичную форму на плоскости
B(x,y)=x^2-w^2 y^2=(x-wy)(x+wy),
где w=(1+\sqrt{5})/2. Тогда ненулевые значения |B(p,q)| отделены от нуля.
Пример 1. Давайте рассмотрим квадратичную форму на плоскости
B(x,y)=x^2-w^2 y^2=(x-wy)(x+wy),
где w=(1+\sqrt{5})/2. Тогда ненулевые значения |B(p,q)| отделены от нуля.
Victor Kleptsyn
М
18:42
Математические байки
Действительно, например, для натуральных p и q величина
|w-p/q|
не может быть меньше, чем 1/(5q^2) — что можно увидеть или через цепные дроби, или "вручную" — " квадратичную иррациональность нельзя приблизить лучше, чем const/q^2 ". Потому что при подстановке (p/q) в квадратный трёхчлен f(z)=z^2-z-1, корнем которого является w, мы получаем дробь со знаменателем q^2 и числителем не меньше 1 по модулю — а если значение |f(p/q)| "большое", то и |w-p/q| большое, ибо теорема Лагранжа.
Так вот — раз |w-p/q| не меньше, чем 1/(5q^2), то |p-wq| не меньше 1/5q, и значит, произведение
|B(p,q)|= |p-wq| |p+wq|
не меньше 1/5.
|w-p/q|
не может быть меньше, чем 1/(5q^2) — что можно увидеть или через цепные дроби, или "вручную" — " квадратичную иррациональность нельзя приблизить лучше, чем const/q^2 ". Потому что при подстановке (p/q) в квадратный трёхчлен f(z)=z^2-z-1, корнем которого является w, мы получаем дробь со знаменателем q^2 и числителем не меньше 1 по модулю — а если значение |f(p/q)| "большое", то и |w-p/q| большое, ибо теорема Лагранжа.
Так вот — раз |w-p/q| не меньше, чем 1/(5q^2), то |p-wq| не меньше 1/5q, и значит, произведение
|B(p,q)|= |p-wq| |p+wq|
не меньше 1/5.
Victor Kleptsyn
М
18:44
Математические байки
Цитируя Маргулиса из сборника лекций филдсовских медалистов (https://www.worldscientific.com/doi/abs/10.1142/9789812564856_0009 ) —
Victor Kleptsyn
М
19:05
Математические байки
Пример 2 — из работы самого Оппенгейма, https://academic.oup.com/qjmath/article-abstract/4/1/54/1568503 . Он очень похож на предыдущий, но в этот раз форма будет принимать маленькие положительные значения и не будет — маленьких отрицательных.
А именно — достаточно взять
B(p,q)=pq-wq^2 = q (p-wq),
где разложение константы w в цепную дробь,
w=[a_0; a_1,a_2,a_3,...]
таково, что нечётные его элементы a_{2k-1} равномерно ограничены, а чётные a_{2k} стремятся к плюс бесконечности.
Тогда подходящие дроби (p_i,q_i), полученные обрубанием цепной дроби для w после a_i с нечётным i=2k-1, приближают w с избытком, меньшим
1/(q_i q_{i+1}) — и потому соответствующие положительные значения
B(p_i,q_i) =q_i (p_i-q_i w) < q_i/q_{i+1} < 1/a_{i+1}
стремятся к нулю. А из-за ограниченности нечётных элементов цепной дроби соответствующие отрицательные значения к нулю не подходят.
А именно — достаточно взять
B(p,q)=pq-wq^2 = q (p-wq),
где разложение константы w в цепную дробь,
w=[a_0; a_1,a_2,a_3,...]
таково, что нечётные его элементы a_{2k-1} равномерно ограничены, а чётные a_{2k} стремятся к плюс бесконечности.
Тогда подходящие дроби (p_i,q_i), полученные обрубанием цепной дроби для w после a_i с нечётным i=2k-1, приближают w с избытком, меньшим
1/(q_i q_{i+1}) — и потому соответствующие положительные значения
B(p_i,q_i) =q_i (p_i-q_i w) < q_i/q_{i+1} < 1/a_{i+1}
стремятся к нулю. А из-за ограниченности нечётных элементов цепной дроби соответствующие отрицательные значения к нулю не подходят.
Victor Kleptsyn
М
19:07
Математические байки
Так что в размерности 2 требований выше ещё не хватает. Так вот: давайте, в-четвёртых, попросим, чтобы размерность n была бы не меньше 3.
Гипотеза Оппенгейма. Невырожденная, индефинитная [не-знакоопределённая], иррациональная форма в размерности n, не меньшей 3, принимает на Z^n всюду плотное множество значений.
Гипотеза Оппенгейма. Невырожденная, индефинитная [не-знакоопределённая], иррациональная форма в размерности n, не меньшей 3, принимает на Z^n всюду плотное множество значений.
Victor Kleptsyn
М
19:15
Математические байки
И первое интересное утверждение тут — это её эквивалентная переформулировка. Оказывается, что достаточно попросить, чтобы форма принимала сколь угодно близкие к нулю ненулевые значения. С одной стороны, если уж множество значений в целых точках будет плотным, то там будут сколь угодно близкие к нулю значения. Но как пройти в обратную сторону?
Victor Kleptsyn
М
19:17
Математические байки
Половина ответа: если значение B(v) маленькое, то на множестве пропорциональных v векторов мы получим множество значений
B(kv)=k^2 B(v),
и соответствующую полупрямую (положительную или отрицательную) сжатое умножением на B(v) множество квадратов "засевает" достаточно плотно (тем плотнее, чем меньше |B(v)|).
B(kv)=k^2 B(v),
и соответствующую полупрямую (положительную или отрицательную) сжатое умножением на B(v) множество квадратов "засевает" достаточно плотно (тем плотнее, чем меньше |B(v)|).
Victor Kleptsyn
М
19:19
Математические байки
Но — а что делать со значениями другого знака? Мы видели (пример 2), что на плоскости, вообще говоря, ничего — там может быть так, что маленьких значений другого знака и впрямь нет.
Victor Kleptsyn
М
19:21
Математические байки
Оказывается, что начиная с размерности 3, из наличия маленьких значений одного знака следует наличие маленьких значений другого знака. И тут я пока просто процитирую две теоремы из той же работы Оппенгейма —
Victor Kleptsyn
М
19:57
Математические байки
Так вот — гипотезу Оппенгейма в конце 1980-ых доказал Маргулис. И в следующий я собираюсь сказать пару слов о том, какая тут возникает геометрия и при чём тут решётки и группы Ли.
Да, for the record: насколько я понимаю, исходная формулировка гипотезы Оппенгейма в 1929 была другой, там была размерность не ниже 5, что мотивировалось теоремой Мейера о том, что в такой размерности индефинитная форма с целыми коэффициентами нетривиально представляет ноль. К её окончательному виду приложил руку Дэвенпорт — кстати, он же c Heilbronn-ом в 1946-м доказал её в размерности >= 5 для диагональных форм — см. https://londmathsoc.onlinelibrary.wiley.com/doi/abs/10.1112/jlms/s1-21.3.185 — и вместе с D. Ridout в 1958-м в размерности >= 21 без этого ограничения — см.
https://londmathsoc.onlinelibrary.wiley.com/doi/abs/10.1112/plms/s3-9.4.544 . Я не уверен, что готов тут делать аккуратный исторический обзор — так что помните, пожалуйста, что кто-то тут наверняка остаётся "за кулисами" моего рассказа...
Да, for the record: насколько я понимаю, исходная формулировка гипотезы Оппенгейма в 1929 была другой, там была размерность не ниже 5, что мотивировалось теоремой Мейера о том, что в такой размерности индефинитная форма с целыми коэффициентами нетривиально представляет ноль. К её окончательному виду приложил руку Дэвенпорт — кстати, он же c Heilbronn-ом в 1946-м доказал её в размерности >= 5 для диагональных форм — см. https://londmathsoc.onlinelibrary.wiley.com/doi/abs/10.1112/jlms/s1-21.3.185 — и вместе с D. Ridout в 1958-м в размерности >= 21 без этого ограничения — см.
https://londmathsoc.onlinelibrary.wiley.com/doi/abs/10.1112/plms/s3-9.4.544 . Я не уверен, что готов тут делать аккуратный исторический обзор — так что помните, пожалуйста, что кто-то тут наверняка остаётся "за кулисами" моего рассказа...
Victor Kleptsyn
М
20:00
Математические байки
А на сегодня это кажется хорошим моментом, чтобы прекратить дозволенные речи.
Victor Kleptsyn
М
20:32
Математические байки
Ох...
Victor Kleptsyn
М
12 April 2020
М
М
16:58
Математические байки
Вспоминая Конвея: одна из его лекций, которые я услышал (на одной из бременско-лионских летних школ, http://www.issmys.eu/previous-year ) была о лексикографических кодах. Давайте я сначала расскажу эту конструкцию так, как тогда рассказывал он сам.
Victor Kleptsyn
М
17:00
Математические байки
Для начала — чуть-чуть общих слов о кодах, исправляющих ошибки (если вы с ними уже встречались — это можно спокойно пропустить).
Есть блочные коды — когда есть некоторый алфавит A, размер блока n, и подмножество S кодовых слов среди всех слов A^n длины n. На словах есть расстояние Хэмминга — это число мест, в которых они различаются. И кодовое расстояние d — это наименьшее расстояние между двумя словами кода. Передавая сообщение, мы его кодируем в |S|-ичной системе счисления и передаём, пересылая словами из S. И чем больше кодовое расстояние — тем устойчивее код к помехам.
Есть блочные коды — когда есть некоторый алфавит A, размер блока n, и подмножество S кодовых слов среди всех слов A^n длины n. На словах есть расстояние Хэмминга — это число мест, в которых они различаются. И кодовое расстояние d — это наименьшее расстояние между двумя словами кода. Передавая сообщение, мы его кодируем в |S|-ичной системе счисления и передаём, пересылая словами из S. И чем больше кодовое расстояние — тем устойчивее код к помехам.
Victor Kleptsyn
М
17:00
Математические байки
Простейший пример — алфавит из 0 и 1, сообщения длины n состоят из собственно сообщения в первых (n-1), последний бит это "бит контроля чётности": сумма всех предыдущих mod 2.
Кодовое расстояние d=2, поэтому если при передаче происходит одна ошибка, мы её обнаруживаем — но не можем исправить, потому что не знаем, какой бит поменялся.
Кодовое расстояние d=2, поэтому если при передаче происходит одна ошибка, мы её обнаруживаем — но не можем исправить, потому что не знаем, какой бит поменялся.
Victor Kleptsyn
М
17:04
Математические байки
Следующий стандартный пример — это код Хэмминга. Это код из 16 слов на блоках длины n=7. Но перечислять 16 слов неудобно — и есть отдельный удобный класс кодов, линейные. Это коды, у которых множества слов являются линейным подпространством; соответственно, достаточно задать его базис (а координаты разложения передаваемой строки по нему будут независимыми битами/символами).
Матрица, строки которой есть элементы этого базиса, называется порождающей матрицей кода; вот порождающая матрица кода Хэмминга —
(1 0 0 0 0 1 1)
(0 1 0 0 1 0 1)
(0 0 1 0 1 1 0)
(0 0 0 1 1 1 1)
Матрица, строки которой есть элементы этого базиса, называется порождающей матрицей кода; вот порождающая матрица кода Хэмминга —
(1 0 0 0 0 1 1)
(0 1 0 0 1 0 1)
(0 0 1 0 1 1 0)
(0 0 0 1 1 1 1)
Victor Kleptsyn
М
17:05
Математические байки
Кстати, несложно видеть, что в этой матрице первые 4 столбца образуют тождественную матрицу; поэтому первые четыре бита (они же коэффициенты разложения по этому базису) можно считать самим сообщением, а последние три — аналогом "контрольной суммы", контролирующими передачу первых битов и друг друга.
Victor Kleptsyn
М
17:06
Математические байки
И несложное упражнение — проверить, что для кода Хэмминга d=3. Поэтому если при передаче происходит одна ошибка, можно не только обнаружить факт ошибки, но и её исправить. Действительно, из-за неравенства треугольника ни от какого слова не будут два слова на расстоянии 1 (иначе расстояние между ними было бы не больше 1+1=2<d=3).
Victor Kleptsyn
М
17:08
Математические байки
Соответственно, конечно же, хочется d побольше, но чтобы размерность кода не сильно падала. Потому что код S={00000,11111} под названием "повторить пять раз", конечно, имеет d=5 и потому исправляет две ошибки, но пропускную способность канала в те же 5 раз уменьшает.
Victor Kleptsyn
М
17:10
Математические байки
Ну и тут есть много большой красивой науки — куда я не пойду, хотя оставлю ссылку на лекцию Шеня (https://www.youtube.com/watch?v=DNCpIo1Gjco ) и на соответствующий рассказ на Мат. Этюдах (где кодируется уже не дискретным алфавитом) — https://www.etudes.ru/ru/etudes/contact-number/
Victor Kleptsyn
М
17:16
Математические байки
Так вот, используя понятия выше как мотивировку, рассмотрим вот такую странную конструкцию. Пусть у нас есть бесконечный алфавит A={0,1,2,3,...} из неотрицательных целых чисел. Рассмотрим слова в таком алфавите, бесконечные влево — как в конструкции p-адических чисел. И зафиксируем "кодовое расстояние" — число d>0.
Victor Kleptsyn
М
17:17
Математические байки
После чего будем "жадным образом" строить код S — добавляя каждый раз лексикографически первое слово, которое находится на расстоянии хотя бы d от всех уже построенных.
Victor Kleptsyn
М
17:19
Математические байки
Возьмём для примера (как тогда взял Конвей) d=3.
Victor Kleptsyn
М
17:20
Математические байки
Тогда первыми словами, которые мы добавим, будут
000000
000111
000222
000333
и так далее.
000000
000111
000222
000333
и так далее.
Victor Kleptsyn
М
17:21
Математические байки
Казалось бы, мы будем добавлять только их. Но — давайте "мыслить трансфинитно": добавим все эти слова (пусть их и бесконечное число), и посмотрим, какое слово мы добавим после них.
Victor Kleptsyn
М
17:24
Математические байки
Ответ — это слово
001012.
Потому что из (лексикографически самых младших из ещё не покрытых) слов 0010** мы не можем себе позволить заменить первую звёздочку нулём — будем на расстоянии не больше 2 до слова 000000, а из слов 00101* нам не подходят ни *=0 (из-за того же слова из нулей), ни *=1 (из-за слова 000111), а вот 001012 подходит, вот мы его и берём.
001012.
Потому что из (лексикографически самых младших из ещё не покрытых) слов 0010** мы не можем себе позволить заменить первую звёздочку нулём — будем на расстоянии не больше 2 до слова 000000, а из слов 00101* нам не подходят ни *=0 (из-за того же слова из нулей), ни *=1 (из-за слова 000111), а вот 001012 подходит, вот мы его и берём.
Victor Kleptsyn
М
17:32
Математические байки
Можно продолжить заполнять этот код — и это хорошее упражнение (которое выглядит занудным, если его делает кто-нибудь ещё, но которое захватывает, когда его делаешь с листочком бумаги). Давайте я напишу ближайшие несколько кодов, которые появятся:
001012 — мы его уже видели, затем
001103
001230
001321
001012 — мы его уже видели, затем
001103
001230
001321
Victor Kleptsyn
М
17:34
Математические байки
Затем пойдут
001456
001547
001674
001765
001456
001547
001674
001765
Victor Kleptsyn
М
17:43
Математические байки
И когда мы, проявив упорство, добавим всё бесконечное число слов вида 001*** — первым словом вида 002*** будет
002023.
Потому что
00200* слишком близко к 000000,
00201* слишком близко к 001012,
002020 — опять к 000000,
002021 — к 001321 (и это легко пропустить),
002022 — к 000222, ну и
002023 — то, что нужно.
002023.
Потому что
00200* слишком близко к 000000,
00201* слишком близко к 001012,
002020 — опять к 000000,
002021 — к 001321 (и это легко пропустить),
002022 — к 000222, ну и
002023 — то, что нужно.
Victor Kleptsyn
М
17:44
Математические байки
Так вот, мы всё это делали не просто так!
Victor Kleptsyn
М
17:45
Математические байки
In reply to this message
Уже на этих словах можно было увидеть какую-то регулярность — и начинать "копать" и разбираться, что же тут интересное.
Victor Kleptsyn
М
17:54
Математические байки
Но интересного больше. Теорема, которую рассказывал Конвей на лекции —
Теорема. Можно так ввести на неотрицательных целых числах сложение и умножение (превратив их в поле), что построенный код будет линейным.
Теорема. Можно так ввести на неотрицательных целых числах сложение и умножение (превратив их в поле), что построенный код будет линейным.
Victor Kleptsyn
М
17:55
Математические байки
Конечно же, сложение и умножение получаются нестандартными — а поле будет характеристики 2.
Victor Kleptsyn
М
18:02
Математические байки
На самом деле, это поле будет объединением "возрастающей башни" полей из 2^{2^k} элементов (поле из p^m элементов это подполе p^r элементов, если r это степень m).
Более того, сложение тут — это то самое ним-сложение (побитовое сложение двоичных записей), которым решается задача о выигрышных позициях в игре в ним.
Более того, сложение тут — это то самое ним-сложение (побитовое сложение двоичных записей), которым решается задача о выигрышных позициях в игре в ним.
Victor Kleptsyn
М
18:21
Математические байки
In reply to this message
И вот эта теорема совершенно удивительна: вроде бы, мы начинали с лексикографического порядка — а в результате на натуральных числах возникла структура поля, а найденные коды оказались образующими линейное пространство.
Victor Kleptsyn
М
18:44
Математические байки
Собственно, если взять вместо бесконечного алфавита — алфавит из B=2^{2^k} символов, — а слова ограничить конечной длиной n — то мы получим часть этого кода: слова, у которых лишь последние n символов ненулевые, и которые не выходят за алфавит A={0,1,...,B-1}. И это уже совсем ситуация кодов, с которой этот рассказ начинался.
Victor Kleptsyn
М
18:48
Математические байки
Например, при B=4 (то есть k=2) и n=6 наш код начнётся со слов
000000
000111
000222
000333
001012
001103
001230
001321
002023
002132
...
000000
000111
000222
000333
001012
001103
001230
001321
002023
002132
...
Victor Kleptsyn
М
18:49
Математические байки
И если верить в теорему выше — то слово 002023 должно быть равно 2*001012, где множитель два — элемент поля из 4 элементов.
Victor Kleptsyn
М
18:52
Математические байки
И вот мы получаем "2*2=3" в поле из 4 элементов {0,1,2,3} — только обычно, конечно, никто не обозначает его элементы 2 и 3, потому что 2 это вовсе не 1+1 (которое там равно нулю).
Victor Kleptsyn
М
18:55
Математические байки
Но соотношения мы получаем как раз какие надо: в поле из 4 элементов, кроме 0 и 1, для которых 1+1=0, есть ещё два элемента, a и b (те самые наши "2" и "3"), причём a^2=b, b^2=a, ab=1, a+1=b, b+1=a.
Victor Kleptsyn
М
18:59
Математические байки
То, что ab=1, видно, например, из
2* 001321 = 002132 —
в левой части мы знаем всё, кроме "2*3".
2* 001321 = 002132 —
в левой части мы знаем всё, кроме "2*3".
Victor Kleptsyn
М
19:04
Математические байки
Вот кусочек из работы Конвея и Слоана, "Lexicographic Codes: Error-Correcting Codes from Game Theory" — посвящённый как раз этим утверждениям:
Victor Kleptsyn
М
19:11
Математические байки
Для алфавита из {0,1} лексикографические коды рассматривал задолго до того Левенштейн — см. http://mi.mathnet.ru/dan39976 — но связи с теорией игр у него из-за этого не было (а Конвей со Слоаном о его работе, очевидно, не знали).
Victor Kleptsyn
М
19:14
Математические байки
Интересно, что такая "жадная" процедура позволяет породить как код Хэмминга — что заметил ещё Левенштейн — так и код Голея, что заметили Конвей со Слоаном:
Victor Kleptsyn
М
М
19:17
Математические байки
Тот самый код Голея, который применялся для передачи изображений от Вояджеров — который за счёт сокращения скорости вдвое (12 бит передаётся 24-мя) позволяет исправить 3 ошибки в группе (и обнаружить, хоть и не исправить, наличие четырёх: у него кодовое расстояние 8) — https://en.wikipedia.org/wiki/Binary_Golay_code#NASA_deep_space_missions
Victor Kleptsyn
М
19:41
Математические байки
Возвращаясь к ним-сложению: если взять d=2, то становится понятно, что это близкая история. А именно: d=2 означает, что мы последовательно (в словарном порядке) перечисляем варианты первых (n-1) букв — и пытаемся их дополнить последней буквой — наименьшей из тех, которая ещё не встречалась раньше для слов, отличающихся лишь в одной из первых (n-1) букв.
Victor Kleptsyn
М
19:43
Математические байки
И если посмотреть — то это то же самое, как устроено перечисление проигрышных позиций при игре в ним (есть кучки камней, ход — взять любое ненулевое число камней из любой одной кучки, проигрывает тот, кто не может сделать ход, то есть перед кем взяли последний камень).
Victor Kleptsyn
М
20:04
Математические байки
In reply to this message
Собственно, сопоставив слову
003451
игру ним с кучками из 3, 4, 5 и 1 камня, мы увидим, что разрешённый ход это как раз уменьшение любой из координат, а условие, что ни одним разрешённым ходом нельзя попасть в слово кода (запрет на расстояние 1) как раз и значит, что из позиции нет хода в проигрышную — и потому она сама проигрышная.
003451
игру ним с кучками из 3, 4, 5 и 1 камня, мы увидим, что разрешённый ход это как раз уменьшение любой из координат, а условие, что ни одним разрешённым ходом нельзя попасть в слово кода (запрет на расстояние 1) как раз и значит, что из позиции нет хода в проигрышную — и потому она сама проигрышная.
Victor Kleptsyn
М
20:05
Математические байки
А ход рассуждений с "наименьшим ещё не названным" для последнего символа соответствует доказательству теоремы Шпрага-Гранди — и принципу "наименьшего исключённого".
Victor Kleptsyn
13 April 2020
М
12:26
Математические байки
Да — мы тут потихоньку перешли от теории кодирования в область комбинаторной теории игр. (Где, кстати, книги Конвея "On Numbers and Games" и его же с Берлекампом и Ги "Winning Ways for your Mathematical Plays" — совершеннейшая классика.)
Ну и, наверное, до того, как переходить к этому рассказу, я показать несколько фотографий Рины Сергеевой с тех летних школ, на которых мы с Конвеем пересекались.
Ну и, наверное, до того, как переходить к этому рассказу, я показать несколько фотографий Рины Сергеевой с тех летних школ, на которых мы с Конвеем пересекались.
Victor Kleptsyn
М
12:27
Математические байки
In reply to this message
Вот тут — https://www.flickr.com/photos/lemezza/7958436406/in/album-72157631334930426/ — Конвей рассказывает про те самые лексикографические коды. В левой части доски как раз идёт выписывание слов, которые мы видели — а в правом верхнем углу доски можно даже разобрать "LEXICODE".
Victor Kleptsyn
М
12:28
Математические байки
А вот тут — https://www.flickr.com/photos/lemezza/11280987216/in/album-72157638495119084/ —
Конвей в окружении участников. Собственно, это на всех школах было перманентное состояние Конвея: быть окружённым участниками, которым он что-то рассказывает, начиная с завтрака и зачастую заканчивая заполночь (и, конечно, включая завтраки, обеды и ужины!).
Конвей в окружении участников. Собственно, это на всех школах было перманентное состояние Конвея: быть окружённым участниками, которым он что-то рассказывает, начиная с завтрака и зачастую заканчивая заполночь (и, конечно, включая завтраки, обеды и ужины!).
Victor Kleptsyn
М
12:35
Математические байки
Вот тут — https://www.flickr.com/photos/lemezza/7902531034/in/album-72157631334930426/ — Конвей играет в футбол. Но не в обычный, а в придуманный им: см. https://en.wikipedia.org/wiki/Phutball
Гил Калаи вспоминает про эту игру (см. https://www.scottaaronson.com/blog/?p=4732#comment-1836693 ):
"<...>Conway set a special rule for me: Everytime I am convinced that I loose, we can switch sides. Needless to say that we switched sides several times; I was sure that my position is desperate beyond repair, we switched sides, and shortly afterward I was again sure that my position in the game is beyond repair.<...>"
А вот что пишет (см. https://terrytao.wordpress.com/2020/04/12/john-conway/ ) Теренс Тао:
"<...>I still remember being repeatedly obliterated in that game, which was a healthy and needed lesson in humility for me (and several of my fellow graduate students) at the time.<...>"
Гил Калаи вспоминает про эту игру (см. https://www.scottaaronson.com/blog/?p=4732#comment-1836693 ):
"<...>Conway set a special rule for me: Everytime I am convinced that I loose, we can switch sides. Needless to say that we switched sides several times; I was sure that my position is desperate beyond repair, we switched sides, and shortly afterward I was again sure that my position in the game is beyond repair.<...>"
А вот что пишет (см. https://terrytao.wordpress.com/2020/04/12/john-conway/ ) Теренс Тао:
"<...>I still remember being repeatedly obliterated in that game, which was a healthy and needed lesson in humility for me (and several of my fellow graduate students) at the time.<...>"
Victor Kleptsyn
М
12:42
Математические байки
Ещё замечательное из той же записи Тао:
"I also recall Conway spending several weeks trying to construct a strange periscope-type device to try to help him visualize four-dimensional objects by giving his eyes vertical parallax in addition to the usual horizontal parallax, although he later told me that the only thing the device made him experience was a headache."
"I also recall Conway spending several weeks trying to construct a strange periscope-type device to try to help him visualize four-dimensional objects by giving his eyes vertical parallax in addition to the usual horizontal parallax, although he later told me that the only thing the device made him experience was a headache."
Victor Kleptsyn
М
12:56
Математические байки
Вот тут — https://www.flickr.com/photos/lemezza/7924971264/in/album-72157631334930426/ — Конвей рассказывает про FRACTRAN — придуманный им "арифметический" язык программирования:
https://en.wikipedia.org/wiki/FRACTRAN .
Давайте я напишу об этом — благо, что это история короткая.
https://en.wikipedia.org/wiki/FRACTRAN .
Давайте я напишу об этом — благо, что это история короткая.
Victor Kleptsyn
М
12:57
Математические байки
Программа на ФРАКТРАНе — это конечный упорядоченный набор дробей,
(p_1/q_1, p_2/q_2,..., p_k/q_k).
"Состояние компьютера" в каждый момент времени — это некоторое натуральное число A.
(p_1/q_1, p_2/q_2,..., p_k/q_k).
"Состояние компьютера" в каждый момент времени — это некоторое натуральное число A.
Victor Kleptsyn
М
13:02
Математические байки
Правило перехода — на каждом такте мы идём по набору дробей слева направа, пытаясь найти такую дробь p_j/q_j, при умножении на которую состояние компьютера останется натуральным. Как только находим — объявляем это произведение
A':=A*p_j/q_j
новым состоянием компьютера.
A':=A*p_j/q_j
новым состоянием компьютера.
Victor Kleptsyn
М
13:40
Математические байки
Если ни на одну дробь из набора домножить так, чтобы остаться в натуральных числах, нельзя — программа останавливается.
Понятно, что при этом хорошо заменять числа на их разложения на простые множители — и, например, считать, что чтобы подать на вход программы пару (a,b), нужно взять начальное состояние A=2^a * 3^b, а про результат договориться, что им будет степень пятёрки после остановки.
Например, задача удвоения решается программой из одной дроби: (25/2), тогда из 2^a мы сделаем 5^{2a}.
Задача сложения — дробями (5/2,5/3): начав с
2^a * 3^b, мы получаем 5^{a+b}.
Понятно, что при этом хорошо заменять числа на их разложения на простые множители — и, например, считать, что чтобы подать на вход программы пару (a,b), нужно взять начальное состояние A=2^a * 3^b, а про результат договориться, что им будет степень пятёрки после остановки.
Например, задача удвоения решается программой из одной дроби: (25/2), тогда из 2^a мы сделаем 5^{2a}.
Задача сложения — дробями (5/2,5/3): начав с
2^a * 3^b, мы получаем 5^{a+b}.
Victor Kleptsyn
М
13:46
Математические байки
In reply to this message
Хорошее упражнение — написать на этом языке "умножение", переводящее 2^a*3^b в 5^{ab}.
А программа, которую написал на доске Конвей, никогда не останавливалась — зато степени двойки, через которые она проходила, были в точности всеми числами вида 2^p, где p — простое.
А программа, которую написал на доске Конвей, никогда не останавливалась — зато степени двойки, через которые она проходила, были в точности всеми числами вида 2^p, где p — простое.
Victor Kleptsyn
14 April 2020
М
20 April 2020
М
12:19
Математические байки
На N+1 несколько дней назад вышел наш с Раскиным текст про Конвея —
https://nplus1.ru/material/2020/04/16/on-conway
https://nplus1.ru/material/2020/04/16/on-conway
Victor Kleptsyn
М
12:21
Математические байки
А ещё коллеги напомнили про текст Конвея и Шипмана про разные доказательства иррациональности корня из 2 —
Victor Kleptsyn
М
12:21
Математические байки
Н
Непрерывное математическое образование 15.10.2017 19:24:39
Вот такой есть текст Конвея и Шипмана про разные доказательства иррациональности корня из 2
Victor Kleptsyn
М
12:23
Математические байки
И доказательства там обсуждаются действительно разные! Кроме стандартного доказательства с делимостью — вот такое доказательство с наложением квадратов:
Victor Kleptsyn
М
12:24
Математические байки
Если квадрат со стороной p равен по площади двум квадратам со стороной q, то вот меньшая аналогичная конфигурация: два пустых квадрата со стороной (p-q) по площади равны закрытому дважды квадрату в центре со стороной q-(p-q)=(2q-p).
Victor Kleptsyn
М
12:29
Математические байки
И если кажется, что такое доказательство применимо только к корню из 2 — то вот такие же рассуждения для корня из трёх и для корня из 5 (точнее, для золотого сечения):
Victor Kleptsyn
М
12:34
Математические байки
И ещё два классных доказательства.
Аналитическое: пусть корень из 2 рационален. Возведём \sqrt{2}-1 в большую-большую степень. С одной стороны, получаются сколь угодно малые положительные числа. С другой, после раскрытия скобок получаем выражение вида a\sqrt{2}+b, где a и b целые, поэтому она не может быть меньше 1/D, где D — знаменатель корня из двух. Противоречие.
Аналитическое: пусть корень из 2 рационален. Возведём \sqrt{2}-1 в большую-большую степень. С одной стороны, получаются сколь угодно малые положительные числа. С другой, после раскрытия скобок получаем выражение вида a\sqrt{2}+b, где a и b целые, поэтому она не может быть меньше 1/D, где D — знаменатель корня из двух. Противоречие.
Victor Kleptsyn
М
12:37
Математические байки
Как легко видеть, оно же показывает, что корень любой степени из любого натурального числа либо натуральный, либо иррациональный — достаточно вычесть целую часть и возводить разность во всё большие степени.
Victor Kleptsyn
М
12:40
Математические байки
И ещё одно — через обратные: если \sqrt{2}=P/Q, то он же равен 2/\sqrt{2}=2Q/P. Тогда равны их дробные части p/Q=q/P, то есть P/Q=p/q, где p и q меньше. И мы опять запустили процедуру спуска — так что если предположить, что P и Q были наименьшими, то вот и получается противоречие.
Victor Kleptsyn
М
12:43
Математические байки
И это последнее доказательство — из книги Конвея и Ги, "The Book of Numbers".
Victor Kleptsyn
М
12:47
Математические байки
Да — если уж я пересказываю эти доказательства, то "доказательство складыванием" тоже симпатичное:
Victor Kleptsyn
М
12:48
Математические байки
Прикладывание катета к гипотенузе приводит к появлению меньшего треугольника — опять с целыми сторонами.
Victor Kleptsyn
М
12:59
Математические байки
Да, в трёх доказательствах — folding, переворачивание и квадраты — для корня из двух операция спуска на самом деле одна и та же:
из P и Q делается (2Q-P) и (P-Q).
из P и Q делается (2Q-P) и (P-Q).
Victor Kleptsyn
М
14:03
Математические байки
In reply to this message
Ещё — читая эту работу, я поймал себя на желании взять ручку и бумагу и сделать список доказательств с краткими комментариями. Дочитав до конца, обнаружил, что авторы уже об этом позаботились:
Victor Kleptsyn
25 April 2020
М
17:22
Математические байки
In reply to this message
Федор Петров напомнил про доказательство Рождественской теоремы Ферма, немного похожее на доказательство через квадраты выше — только вместо бесконечного спуска там инволюция.
Victor Kleptsyn
М
17:23
Математические байки
Рождественская теорема Ферма говорит о том, какие простые представимы в виде суммы двух квадратов: это 2 и простые вида 4k+1 (и только они).
Victor Kleptsyn
М
17:27
Математические байки
У неё есть стандартное доказательство через гауссовы целые числа: сначала доказываем, что в кольце Z[i]=Z+iZ тоже есть алгоритм Евклида, и потому там есть однозначность разложения на простые.
Потом — что по модулю p=4k+1 есть корень из (-1), потому что если разбивать все ненулевые остатки (а их p-1=4k) на четвёрки (x,1/x,-x,-1/x), то одна такая "четвёрка" схлопнется в двойку (1,-1), а значит, должна схлопнуться и ещё одна. А это может случиться, только если по модулю p есть корень из (-1).
Кстати, так же проверяется, что по модулю простых вида 4k+3 корня из (-1) не бывает (потому что там p-1=4k+2 ненулевых остатка как раз разбиваются на двойку (1,-1) и четвёрки — а места для ещё одной двойки не остаётся).
Ну а дальше из соотношения r^2+1=(r+i)(r-i)=mp и основной теоремы арифметики в Z[i] выводится, что p не простое — и значит, p=(a+bi)(a-bi), то есть p=a^2+b^2.
Потом — что по модулю p=4k+1 есть корень из (-1), потому что если разбивать все ненулевые остатки (а их p-1=4k) на четвёрки (x,1/x,-x,-1/x), то одна такая "четвёрка" схлопнется в двойку (1,-1), а значит, должна схлопнуться и ещё одна. А это может случиться, только если по модулю p есть корень из (-1).
Кстати, так же проверяется, что по модулю простых вида 4k+3 корня из (-1) не бывает (потому что там p-1=4k+2 ненулевых остатка как раз разбиваются на двойку (1,-1) и четвёрки — а места для ещё одной двойки не остаётся).
Ну а дальше из соотношения r^2+1=(r+i)(r-i)=mp и основной теоремы арифметики в Z[i] выводится, что p не простое — и значит, p=(a+bi)(a-bi), то есть p=a^2+b^2.
Victor Kleptsyn
М
17:28
Математические байки
Так вот — это стандартное доказательство, и оно требует некоторого количества техники (хоть и "по делу"). А есть гораздо более простое доказательство представимости простых вида 4k+1 в виде суммы двух квадратов — геометрическая обработка А. В. Спиваком доказательства, предложенного Д. Загиром (в свою очередь, упростившего доказательство Heath-Brown-а).
Victor Kleptsyn
М
17:31
Математические байки
А именно: пусть p=4k+1. Если уж p получится представить в виде суммы квадратов, то один из них будет чётным (а другой нечётным, но это неважно). Поэтому давайте сразу искать представление в виде p=x^2+4y^2.
Victor Kleptsyn
М
17:31
Математические байки
Для этого рассмотрим все возможные представления p в виде p=x^2+4yz, где x,y,z натуральные. И рассмотрим на этом множестве инволюцию — поменяем местами y и z. Так вот, нас интересует неподвижная точка этой инволюции — та, где y=z. (Точка или точки, конечно, но на самом деле она одна).
Victor Kleptsyn
М
17:33
Математические байки
Как можно гарантировать, что неподвижная точка у инволюции есть? Да очень просто — если общее число точек нечётно, то на пары они в любом случае не разобьются, и неподвижная точка будет.
Victor Kleptsyn
М
17:36
Математические байки
А как можно доказывать, что количество точек нечётно? Тоже очень просто — давайте на этом множестве запустим какую-нибудь другую инволюцию, и если у неё будет ровно одна неподвижная точка, а все остальные точки разобьются на пары, то вот их общее число и будет нечётно.
Victor Kleptsyn
М
17:39
Математические байки
А теперь, собственно, изюминка этого рассуждения: вторую инволюцию можно задать формулами — но гораздо лучше задать геометрически. А именно — представлению p=x^2+4yz можно сопоставить этакую "мельницу":
Victor Kleptsyn
М
17:42
Математические байки
(Я взял этот рисунок из записок самого Спивака — http://mmmf.msu.ru/lect/spivak/zagir_!.pdf — см. лекцию 15 тут: http://mmmf.msu.ru/lect/lect8.html )
Victor Kleptsyn
М
17:44
Математические байки
Так вот, на таких "мельницах" есть инволюция, которую проще показать, чем задавать формулами:
Victor Kleptsyn
М
17:44
Математические байки
(Рисунок оттуда же)
Victor Kleptsyn
М
17:45
Математические байки
И почти все "мельницы" разбиваются на пары одинаковой формы:
Victor Kleptsyn
М
17:45
Математические байки
(И опять картинка из того же текста А. В. Спивака)
Victor Kleptsyn
М
17:48
Математические байки
Почти все — кроме одной ситуации.
Если x=y, то у нас нет вариантов, каким выбирать внутренний квадрат, "толстым" или "худым":
Если x=y, то у нас нет вариантов, каким выбирать внутренний квадрат, "толстым" или "худым":
Victor Kleptsyn
М
17:49
Математические байки
Но тогда x^2+4xz=x(x+4z)=p, и в силу простоты p это означает, что x=1.
Victor Kleptsyn
М
17:50
Математические байки
Так что такая неподвижная точка у этой инволюции ровно одна.
Victor Kleptsyn
М
17:50
Математические байки
(А что она есть — это как раз то, что p=4k+1)
Victor Kleptsyn
М
17:51
Математические байки
И вот мы и получили, что число представлений нечётно. Победа: значит, неподвижная точка будет и у меняющей y и z инволюции.
Victor Kleptsyn
М
17:58
Математические байки
Фёдор Петров, собственно, рассказывал о рождественской теореме Ферма позавчера — см. https://www.youtube.com/watch?v=wfTCPPHViWw&feature=youtu.be&t=2193 ; ещё хорошая ссылка это обсуждение на MathOverflow (начинающееся, собственно, с вопроса про то, как понять предложенную Загиром инволюцию) — https://mathoverflow.net/a/299696 ; и по ссылке оттуда — более развёрнутый текст А. В. Спивака, "Крылатые квадраты": http://mmmf.msu.ru/lect/spivak/summa_sq.pdf
Victor Kleptsyn
М
18:02
Математические байки
Ну и — вот то самое "доказательство в один абзац" Д.Загира:
Victor Kleptsyn
М
18:06
Математические байки
In reply to this message
И правда ведь красиво, когда такой абзац формул (очень изящный, но для меня не очень говорящий — ибо непонятно, как до такого можно додуматься) получается превратить в картинку!
Victor Kleptsyn
26 April 2020
М
13:12
Математические байки
Возвращаясь к Конвею — давайте я расскажу о его статье под очень точным названием "A Headache Causing Problem".
Victor Kleptsyn
М
13:14
Математические байки
Итак, задача:
На шляпах (или на лбу) у нескольких людей (Артур, Бертран,...) написаны натуральные числа — так, что каждый видит все числа, кроме своего собственного. А на доске написаны варианты их суммы, среди которых один правильный.
Например, пусть у участников на шляпах написаны просто три двойки — 2, 2, 2, — а на доске написаны 6, 7 и 8.
На шляпах (или на лбу) у нескольких людей (Артур, Бертран,...) написаны натуральные числа — так, что каждый видит все числа, кроме своего собственного. А на доске написаны варианты их суммы, среди которых один правильный.
Например, пусть у участников на шляпах написаны просто три двойки — 2, 2, 2, — а на доске написаны 6, 7 и 8.
Victor Kleptsyn
М
13:15
Математические байки
Картинка из статьи —
Victor Kleptsyn
М
13:15
Математические байки
Их много раз по кругу опрашивают: "знаете ли вы своё число", и ответы ("да" или "нет") слышны всем.
Нужно доказать, что если вариантов на доске не больше, чем людей (скажем, как в примере выше), то рано или поздно кто-нибудь ответит "да".
Нужно доказать, что если вариантов на доске не больше, чем людей (скажем, как в примере выше), то рано или поздно кто-нибудь ответит "да".
Victor Kleptsyn
М
13:22
Математические байки
(И немедленно вспоминаются, конечно, классические задачи про проводника и пассажиров с закопчёнными после туннеля лицами, или про чужеземца и голубоглазых островитян.)
Victor Kleptsyn
М
13:44
Математические байки
А рассуждение тут очень изящное. Авторы вводят слепого арбитра, Zoe, которой известны числа на доске и которая слышит все ответы участников — но которой неизвестно ни одно из чисел на шляпах. И она ведёт таблицу возможных вариантов наборов — вычеркивая те, которые становятся невозможными после услышанных ответов.
Victor Kleptsyn
М
13:47
Математические байки
Так вот, её таблица на самом деле хранит в себе всю информацию, собранную в результате предыдущих ответов — так что очередной отвечающий (допустим, Бертран) может просто посмотреть на неё, найти в ней наборы, совпадающие с видимыми числами им остальных участников, и понять, однозначно ли это определяет его число. Если такой набор один, он говорит "да", иначе "нет".
Victor Kleptsyn
М
13:49
Математические байки
Соответственно, Zoe при очередном ответе "нет" одного из участников вычёркивает из таблицы те наборы, для которых в таблице нет других наборов, отличающихся от данного только на число этого участника:
Victor Kleptsyn
М
13:52
Математические байки
И вот как выглядит таблица для набора сумм (6,7,8) —
Victor Kleptsyn
М
14:01
Математические байки
(Картинка из той же статьи, и про саму статью я ещё скажу — ибо с ней тоже всё интересно.)
На этом рисунке подписаны, правда, только тройки на границе — но понятно, как оно продолжается внутрь. А числа, которыми подписаны вершины этой таблицы, это номер вопроса, на котором этот набор будет вычеркнут. Скажем, все варианты вида (0,b,8-b), идущие вдоль правой стороны этого "треугольника", будут вычеркнуты первым же вопросом к A. Вариант (7,0,1) не будет вычеркнут вопросом к A — но будет вычеркнут следующим за этим вопросом к B. А вариант (7,0,0) будет вычеркнут на третьем вопросе — ибо единственная альтернатива с точки зрения C, (7,0,1), только что исключена.
На этом рисунке подписаны, правда, только тройки на границе — но понятно, как оно продолжается внутрь. А числа, которыми подписаны вершины этой таблицы, это номер вопроса, на котором этот набор будет вычеркнут. Скажем, все варианты вида (0,b,8-b), идущие вдоль правой стороны этого "треугольника", будут вычеркнуты первым же вопросом к A. Вариант (7,0,1) не будет вычеркнут вопросом к A — но будет вычеркнут следующим за этим вопросом к B. А вариант (7,0,0) будет вычеркнут на третьем вопросе — ибо единственная альтернатива с точки зрения C, (7,0,1), только что исключена.
Victor Kleptsyn
М
14:03
Математические байки
Тройка (2,2,2) — одна из четырёх (для сумм (6,7,8)), для которых, чтобы услышать "да", приходится задавать аж 19 вопросов:
Victor Kleptsyn
М
15:10
Математические байки
Собственно, теперь уже легко доказать и общее утверждение. Только его проще доказывать в другую сторону — как утверждение "если есть конфигурация наборов в N-мерном пространстве, таких, что для любого набора и любой координаты есть набор, отличающийся от первого лишь по этой координате, то сумма координат принимает по меньшей мере N+1 значение". Каковое утверждение достаточно применить к той части таблицы Zoe, которая никогда не будет вычеркнута, и получить противоречие.
Victor Kleptsyn
М
15:12
Математические байки
И доказательство легко проводится по индукции по размерности (количеству участников) N. А именно — выделяем одну из координат (например, первую), и смотрим на наборы из конфигурации, где она принимает наименьшее возможное значение a_0.
Victor Kleptsyn
М
15:16
Математические байки
С одной стороны, по оставшимся (N-1) координате эти наборы обладают таким же свойством — поэтому уже там мы видим как минимум (N-1)+1=N различных сумм (к которым добавляется одно и то же a_0).
С другой — посмотрим на наибольшую из этих сумм и на соответствующий набор (a_0,b,c,...). По предположению на всю конфигурацию наборов, мы можем заменить первую координату в наборе и опять получить набор (a', b,c,...) из конфигурации. С другой стороны, a_0 было наименьшим возможным значением первой координаты, так что a'>a_0 и поэтому мы нашли ещё одну — ещё большую — сумму. И вот у нас и нашлись N+1 разная сумма, и доказательство завершено.
С другой — посмотрим на наибольшую из этих сумм и на соответствующий набор (a_0,b,c,...). По предположению на всю конфигурацию наборов, мы можем заменить первую координату в наборе и опять получить набор (a', b,c,...) из конфигурации. С другой стороны, a_0 было наименьшим возможным значением первой координаты, так что a'>a_0 и поэтому мы нашли ещё одну — ещё большую — сумму. И вот у нас и нашлись N+1 разная сумма, и доказательство завершено.
Victor Kleptsyn
М
15:51
Математические байки
И — возвращаясь к самой статье. У неё три автора: Конвей, Патерсон и... Москва (СССР) (!) —
https://www.tandfonline.com/doi/full/10.1080/00029890.2020.1712168
https://www.tandfonline.com/doi/full/10.1080/00029890.2020.1712168
Victor Kleptsyn
М
15:52
Математические байки
Более того, если кажется, что это опечатка, и что-нибудь не туда вписали — так всё правильно:
Victor Kleptsyn
М
17:18
Математические байки
На самом деле — эта статья исходно была написана в 1977 году, и появилась в сборнике, изданном "частным образом" в подарок Ленстре:
Victor Kleptsyn
М
М
17:24
Математические байки
А пару лет назад Дирк Шляйхер уговорил Конвея её издать и "для широкой публики" — так что она вышла в American Math. Monthly.
Вот тут — https://blog.tanyakhovanova.com/2008/08/a-math-paper-by-moscow-ussr/ — запись 2008 года в блоге Татьяны Ховановой, посвящённая этой статье; там можно увидеть фотографию Конвея, ищущего свой оттиск этой статьи, и собственно скан того оттиска:
http://www.tanyakhovanova.com/BlogStuff/Conway/Headache.pdf
Вот тут — https://blog.tanyakhovanova.com/2008/08/a-math-paper-by-moscow-ussr/ — запись 2008 года в блоге Татьяны Ховановой, посвящённая этой статье; там можно увидеть фотографию Конвея, ищущего свой оттиск этой статьи, и собственно скан того оттиска:
http://www.tanyakhovanova.com/BlogStuff/Conway/Headache.pdf
Victor Kleptsyn
М
17:25
Математические байки
Ну и — благодарности смотрятся отдельно прекрасным образом:
Victor Kleptsyn
27 April 2020
М
13:59
Математические байки
Вчера было сто лет со дня смерти Рамануджана —
Victor Kleptsyn
М
13:59
Математические байки
Н
Непрерывное математическое образование 27.04.2020 11:47:29
http://kvant.mccme.ru/1987/10/zagadka_ramanudzhana.htm
вот такая статья Гиндикина про Рамануджана и его математику пусть здесь будет
вот такая статья Гиндикина про Рамануджана и его математику пусть здесь будет
Victor Kleptsyn
М
18:39
Математические байки
Н
Непрерывное математическое образование 27.04.2020 17:11:06
https://link.springer.com/search?facet-content-type=%22Book%22&package=mat-covid19_textbooks&facet-language=%22En%22&sortOrder=newestFirst&facet-discipline=%22Mathematics%22&showAll=true
Шпрингер раздает бесплатно несколько электронных книг — в т.ч., например, «Proofs from The Book», но совсем не только (спасибо К.Кнопу за ссылку)
Шпрингер раздает бесплатно несколько электронных книг — в т.ч., например, «Proofs from The Book», но совсем не только (спасибо К.Кнопу за ссылку)
Victor Kleptsyn
М
18:39
Математические байки
Н
Непрерывное математическое образование 27.04.2020 17:11:54
Victor Kleptsyn
8 May 2020
М
21:28
Математические байки
Н
Непрерывное математическое образование 08.05.2020 21:28:13
https://8ecm.si/news/69
…премии, тем не менее, объявили уже сейчас:
Karim Adiprasito (Hebrew University of Jerusalem / University of Copenhagen)
Ana Caraiani (Imperial College London)
Alexander Efimov (Steklov, Moscow)
Simion Filip (Chicago)
Aleksandr Logunov (Princeton)
Kaisa Matomäki (Turku)
Phan Thành Nam (LMU Munich)
Joaquim Serra (ETH Zurich)
Jack Thorne (Cambridge)
Maryna Viazovska (EPFL, Lausanne)
…премии, тем не менее, объявили уже сейчас:
Karim Adiprasito (Hebrew University of Jerusalem / University of Copenhagen)
Ana Caraiani (Imperial College London)
Alexander Efimov (Steklov, Moscow)
Simion Filip (Chicago)
Aleksandr Logunov (Princeton)
Kaisa Matomäki (Turku)
Phan Thành Nam (LMU Munich)
Joaquim Serra (ETH Zurich)
Jack Thorne (Cambridge)
Maryna Viazovska (EPFL, Lausanne)
Victor Kleptsyn
12 May 2020
М
17:13
Математические байки
Н
Непрерывное математическое образование 12.05.2020 15:19:22
умер Эрнест Борисович Винберг
с 1961 года работал на мехмате МГУ, многие помнят его лекции и семинар Винберга-Онищика; многочисленные ученики и коллеги Эрнеста Борисовича еще о нем напишут
с 1961 года работал на мехмате МГУ, многие помнят его лекции и семинар Винберга-Онищика; многочисленные ученики и коллеги Эрнеста Борисовича еще о нем напишут
Victor Kleptsyn
М
17:13
Математические байки
Н
Непрерывное математическое образование 12.05.2020 15:34:53
Discoveries, not Inventions — Interview with
Ernest Borisovich Vinberg
Ernest Borisovich Vinberg
Victor Kleptsyn
18 May 2020
М
17:13
Математические байки
EZ
Evgenii Zheltonozhskii🇮🇱 18.05.2020 11:26:22
Victor Kleptsyn
М
17:49
Математические байки
In reply to this message
И в продолжение — вот тут картинка, которая показывает, что происходит:
https://twitter.com/matthen2/status/1262249113384452096
https://twitter.com/matthen2/status/1262249113384452096
Victor Kleptsyn
19 May 2020
М
22:08
Математические байки
E
Elementy.ru 19.05.2020 21:32:58
Первое издание «Математической составляющей» вышло в 2015 году и получило премию «Просветитель». Второе издание существенно дополнено — достаточно сказать, что объем книги вырос в два раза. Мы публикуем три главы из второго издания.
«Складывание карт»
Наверняка вам знакома эта ситуация, когда разложить листочек легко, а при складывании приходится вспоминать, как он был сложен. Есть ли способ складывания, при котором развернутая карта складывалась бы «сама» и не нужно было бы ничего запоминать?
«Цветовые пространства»
Какими могут быть модели цветового пространства? Авторы рассказывают о моделях RGB и CMYK, об их математической основе и об особенностях использования.
«Случайные блуждания»
Теория случайных блужданий началась с открытия в 1827 году броуновского движения. У нее много применений и любопытных следствий. Лауреат Филдсовской премии Станислав Смирнов рассказывает о её роли в экономике и молекулярной физике, а также о связи случайных блужданий и фракталов.
elementy.ru/link/t/mathcomponent
«Складывание карт»
Наверняка вам знакома эта ситуация, когда разложить листочек легко, а при складывании приходится вспоминать, как он был сложен. Есть ли способ складывания, при котором развернутая карта складывалась бы «сама» и не нужно было бы ничего запоминать?
«Цветовые пространства»
Какими могут быть модели цветового пространства? Авторы рассказывают о моделях RGB и CMYK, об их математической основе и об особенностях использования.
«Случайные блуждания»
Теория случайных блужданий началась с открытия в 1827 году броуновского движения. У нее много применений и любопытных следствий. Лауреат Филдсовской премии Станислав Смирнов рассказывает о её роли в экономике и молекулярной физике, а также о связи случайных блужданий и фракталов.
elementy.ru/link/t/mathcomponent
Victor Kleptsyn
21 May 2020
М
10:24
Математические байки
Н
Непрерывное математическое образование 16.05.2020 15:59:48
https://twitter.com/74WTungsteno/status/1261584412946374657
картинка по выходным — про дельтоиду (спасибо В.Клепцыну за ссылочку)
(контекст — можно прочитать в уже упоминавшейся замечательной книге «Прямые и кривые», а также у J.Baez’а)
картинка по выходным — про дельтоиду (спасибо В.Клепцыну за ссылочку)
(контекст — можно прочитать в уже упоминавшейся замечательной книге «Прямые и кривые», а также у J.Baez’а)
Victor Kleptsyn
М
10:25
Математические байки
In reply to this message
Вот ещё одна красивая картинка на эту же тему — спасибо М. Панову:
Victor Kleptsyn
М
М
10:40
Математические байки
И при взгляде на неё видно, что происходит что-то нетривиальное: все нарисованные "гипоциклоиды" катятся друг по другу, и касаясь друг друга, и скользя каждая своими вершинами по следующей. Так что давайте посмотрим аккуратно, что и почему происходит.
Victor Kleptsyn
М
10:56
Математические байки
Для начала — "что": друг по другу без проскальзывания катаются окружности радиусов r, 2r, 3r,..., оставаясь все одновременно касающимися (можно считать, что внутренняя "прижимает" все промежуточные к внешней). На внутренней окружности отмечена точка — и она рисует кривые (гипоциклоиды) на кругах, связанных с этими окружностями.
Можно спросить, конечно, как можно так рисовать одновременно на всех уровнях — ну либо нужно сказать, что точка это лазер, а на каждой окружности частично-прозрачная фоточувствительная бумага, либо сказать, что мы эту картинку рисуем последовательно — рисующая точка это фломастер, а после каждого оборота мы заклеиваем прозрачным диском очередную окружность.
Можно спросить, конечно, как можно так рисовать одновременно на всех уровнях — ну либо нужно сказать, что точка это лазер, а на каждой окружности частично-прозрачная фоточувствительная бумага, либо сказать, что мы эту картинку рисуем последовательно — рисующая точка это фломастер, а после каждого оборота мы заклеиваем прозрачным диском очередную окружность.
Victor Kleptsyn
М
11:06
Математические байки
Теперь ответ "почему они все касаются" простой — но всё-таки не мгновенный. Хотелось бы сказать, что эти кривые касаются друг друга — потому что их рисует одна и та же точка (и ровно в той точке, где она сейчас находится, они и касаются). Но — она их рисует на движущихся кругах.
Victor Kleptsyn
М
11:11
Математические байки
Если бы мы взяли два листа бумаги и начали двигать с постоянной скоростью в двух разных направлениях, а рисующую точку сделали бы вообще неподвижной — то она на этих листах нарисовала бы прямые, пересекающиеся под углом (потому что каждая прямая будет того направления, куда мы тащим соответствующий лист). Поэтому просто словами "да все эти кривые одной и той же точкой нарисованы" нам не отбиться, нужно посмотреть чуть более аккуратно.
Victor Kleptsyn
М
11:19
Математические байки
И тут можно сказать, что при качении без проскальзывания мгновенный центр вращения — точка касания. То есть все скорости в каждом из кругов в данный момент времени направлены так, как если бы он поворачивался вокруг точки касания.
Что, собственно, и логично. Ибо если поверить, что мгновенный центр вращения должен быть (а куда ему деться — если мы знаем теорему Шаля о классификации движений плоскости, так посмотрим, какой поворот переводит колесо в данный момент t в его положение в момент t+\delta, и возьмём предел центров этих поворотов), то этим мгновенным центром должна быть сейчас-неподвижная-точка, а это как раз точка касания.
Что, собственно, и логично. Ибо если поверить, что мгновенный центр вращения должен быть (а куда ему деться — если мы знаем теорему Шаля о классификации движений плоскости, так посмотрим, какой поворот переводит колесо в данный момент t в его положение в момент t+\delta, и возьмём предел центров этих поворотов), то этим мгновенным центром должна быть сейчас-неподвижная-точка, а это как раз точка касания.
Victor Kleptsyn
М
11:20
Математические байки
Собственно, это часто рассказывают на физике — ну и мне вспоминается вот этот кадр из мультфильма "Циклоида" Математических Этюдов (https://www.etudes.ru/ru/etudes/cycloid/ ) —
Victor Kleptsyn
М
11:23
Математические байки
In reply to this message
Тут нарисован ответ на вопрос, как направлена мгновенная скорость попавшего в колесо камушка. Ну и если на этой картинке провести отрезок к точке касания (которая внизу), то как раз и получится опирающийся на (вертикальный) диаметр прямой угол — как и положено углу между вектором скорости и радиус-вектором из центра вращения.
Victor Kleptsyn
М
11:24
Математические байки
In reply to this message
Так вот — наши круги все (в каждый момент времени) касаются друг друга. Поэтому мгновенные скорости у них у всех в любой точке — в частности, в рисующей — сонаправлены (ибо все перпендикулярны радиус-вектору из точки касания).
Victor Kleptsyn
М
11:26
Математические байки
И поэтому и у рисуемых кривых касательные идут в том же (одном и том же для всех) направлении — то есть они касаются.
Victor Kleptsyn
М
11:36
Математические байки
Половина загадки разгадана; давайте теперь перейдём к вершинам. Достаточно разобраться, почему вершины предпоследней (синей) кривой едут по последней, неподвижной (фиолетовой). Потому что для движения, скажем, жёлтой дельтоиды по зелёной астроиде можно просто перейти в (движущуюся) систему отсчёта — сесть на зелёный круг. Там зелёный круг неподвижен, всё, что снаружи, можно выкинуть, а внутри мы видим такую же конфигурацию (окружности катятся с общей точкой касания).
Victor Kleptsyn
М
11:39
Математические байки
In reply to this message
Вершина на синей кривой появляется в тот момент, когда рисующая точка оказывается точкой касания (то есть когда она максимально-внешняя). И дальше эта синяя вершина едет вместе с синей окружностью — двигается по гипоциклоиде.
Victor Kleptsyn
М
11:44
Математические байки
Но если внутри окружности радиуса R рисовать гипоциклоиду окружностью радиуса r1 — то получится то же самое, что если её рисовать окружностью r2=(R-r1), движущейся в другую сторону. Более того, если взять отношение угловых скоростей обратно пропорциональным отношению радиусов — то просто отмеченные точки на рисующих окружностях будут совпадать в каждый момент времени. И вот иллюстрация к этому (опять спасибо М. Панову!) —
Victor Kleptsyn
М
М
11:49
Математические байки
In reply to this message
Рисующая точка (красная) общая для двух окружностей: при таком отношении угловых скоростей радиус-вектор в точку одной окружности из её центра поворачивается так же, как и радиус-вектор в центр другой окружности из центра неподвижной. Вот у нас и получается параллелограмм.
Victor Kleptsyn
М
11:53
Математические байки
Поэтому вершина на синей кривой (радиуса r2=nr) движется так же, как если бы она была отмечена на окружности радиуса r1=R-r2=(n+1)r-nr=r, катящейся в обратную сторону. А она и рисует нашу фиолетовую гипоциклоиду! И кстати, действительно видно, что синие вершины скользят по фиолетовой кривой в обратную сторону.
Victor Kleptsyn
М
12:04
Математические байки
In reply to this message
Вот мы и доказали, что вершины каждой гипоциклоиды скользят по следующей. В частности, прямой отрезок-диаметр (внутри окружности радиуса 2r) скользит по дельтоиде (внутри окружности радиуса 3r) — что мы, собственно, видели и на исходной картинке.
Вот если бы мне это просто сформулировали, как изолированный факт ("длина отрезка касательной к дельтоиде, содержащейся внутри неё, постоянна") — ой не сразу бы я в это поверил (и уж точно загрустил бы от одной мысли о доказательстве грубым счётом).
Вот если бы мне это просто сформулировали, как изолированный факт ("длина отрезка касательной к дельтоиде, содержащейся внутри неё, постоянна") — ой не сразу бы я в это поверил (и уж точно загрустил бы от одной мысли о доказательстве грубым счётом).
Victor Kleptsyn
М
12:07
Математические байки
Ещё несколько красивых иллюстраций (и опять спасибо М. Панову!):
Одна и та же гипоциклоида, только уже "звёздчатая":
Одна и та же гипоциклоида, только уже "звёздчатая":
Victor Kleptsyn
М
М
12:09
Математические байки
А вот — если мы достроим параллелограмм в другую сторону :
Victor Kleptsyn
М
М
12:13
Математические байки
In reply to this message
И цитата на эту тему из 7-й главы "Прямых и кривых" (http://zadachi.mccme.ru/prkr/ , которые выше уже упоминали) —
Victor Kleptsyn
М
12:18
Математические байки
Ещё картинка на эту же тему — циклоидальная передача:
Victor Kleptsyn
М
М
12:18
Математические байки
(а эта картинка из Википедии — https://ru.wikipedia.org/wiki/%D0%A6%D0%B8%D0%BA%D0%BB%D0%BE%D0%B8%D0%B4%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D0%BF%D0%B5%D1%80%D0%B5%D0%B4%D0%B0%D1%87%D0%B0 )
Victor Kleptsyn
М
12:21
Математические байки
И в завершение — вот звёздчатая гипоциклоида с двойным параллелограммом (и двумя рисующими точками на одной из окружностей):
Victor Kleptsyn
М
27 May 2020
М
15:26
Математические байки
Красивое перекладывание:
https://twitter.com/74WTungsteno/status/1265613949485096961/photo/1
https://twitter.com/74WTungsteno/status/1265613949485096961/photo/1
Victor Kleptsyn
29 May 2020
М
12:17
Математические байки
In reply to this message
Давайте я попробую немного рассказать о комплексной динамике — о том, что и почему мы на этих анимациях видим.
Да — я буду пользоваться двумя генераторами фракталов. Во-первых, у Элементов.ру есть совершенно классная серия интерактивных плакатов, https://elementy.ru/posters/ , — и один из них посвящён как раз фракталам; и там можно одновременно смотреть на точку множества Мандельброта и на соответствующее ей множество Жюлиа — https://elementy.ru/posters/fractals/Julia .
Увы, эти плакаты на флеше, который не все современные браузеры любят. :(
А во-вторых, вот этим генератором — http://usefuljs.net/fractals/ .
Да — я буду пользоваться двумя генераторами фракталов. Во-первых, у Элементов.ру есть совершенно классная серия интерактивных плакатов, https://elementy.ru/posters/ , — и один из них посвящён как раз фракталам; и там можно одновременно смотреть на точку множества Мандельброта и на соответствующее ей множество Жюлиа — https://elementy.ru/posters/fractals/Julia .
Увы, эти плакаты на флеше, который не все современные браузеры любят. :(
А во-вторых, вот этим генератором — http://usefuljs.net/fractals/ .
Victor Kleptsyn
М
12:18
Математические байки
Итак, главные герои. Формальные определения такие: пусть задано отображение z->P(z), например, вида z^2+c.
Тогда для любой начальной точки z_0 можно рассмотреть последовательность её итераций — применяя P снова и снова: z_n = P(z_{n-1}).
Так вот, заполненным множеством Жюлиа полинома P называется множество точек z_0, итерации которых не убегают на бесконечность.
(Определение выше общее — но сейчас я его собираюсь применять только к квадратичным отображениям, z->z^2+c.)
Тогда для любой начальной точки z_0 можно рассмотреть последовательность её итераций — применяя P снова и снова: z_n = P(z_{n-1}).
Так вот, заполненным множеством Жюлиа полинома P называется множество точек z_0, итерации которых не убегают на бесконечность.
(Определение выше общее — но сейчас я его собираюсь применять только к квадратичным отображениям, z->z^2+c.)
Victor Kleptsyn
М
12:19
Математические байки
А множеством Мандельброта называется множество таких параметров c, что у отображения
P_c (z) = z^2+c
не убегают на бесконечность итерации начальной точки 0.
P_c (z) = z^2+c
не убегают на бесконечность итерации начальной точки 0.
Victor Kleptsyn
М
12:20
Математические байки
Определение заполненного множества Жюлиа похоже на другие определения фракталов: что-то куда-то итерируется. И из-за итераций естественно ожидать какого-то самоподобия.
А вот определение множества Мандельброта кажется странным: почему речь идёт об итерациях именно точки z=0? И из него совсем не видно, почему должен получаться фрактал.
А вот определение множества Мандельброта кажется странным: почему речь идёт об итерациях именно точки z=0? И из него совсем не видно, почему должен получаться фрактал.
Victor Kleptsyn
М
12:25
Математические байки
Так вот, давайте на всё это посмотрим и с этим разберёмся. Начнём со случая c=0. Тогда мы итерируем
P_0(z)=z^2,
и его итерации достаточно просто описать. А именно, n-я итерация это z^{2^n}, поэтому:
*) точки z с |z|>1 убегают на бесконечность,
*) точки с |z|<1 падают в ноль,
*) а |z|=1 — окружность, остающаяся на месте, и на которой аргумент (из-за возведения в квадрат) за одну итерацию P_0 удваивается.
В частности, заполненное множество Жюлиа — диск |z|<=1:
P_0(z)=z^2,
и его итерации достаточно просто описать. А именно, n-я итерация это z^{2^n}, поэтому:
*) точки z с |z|>1 убегают на бесконечность,
*) точки с |z|<1 падают в ноль,
*) а |z|=1 — окружность, остающаяся на месте, и на которой аргумент (из-за возведения в квадрат) за одну итерацию P_0 удваивается.
В частности, заполненное множество Жюлиа — диск |z|<=1:
Victor Kleptsyn
М
12:26
Математические байки
Слева на этой картинке (с Элементов) множество Мандельброта, с отмеченной (белой) точкой c=0, а справа — соответствующее множество Жюлиа.
Victor Kleptsyn
М
12:27
Математические байки
А что будет, если мы возьмём параметр c явно за пределами множества Мандельброта — например, c=5?
Victor Kleptsyn
М
12:28
Математические байки
Для начала заметим, что если уж какая-то точка z принадлежит заполненному множеству Жюлиа J_c, то она не может быть слишком большой по модулю — иначе модули образов будут только нарастать. Ведь
|P(z)| >= |z|^2 - |c|;
скажем, для |c|<=5 уже при |z|>4 будет |P(z)|>11, потом |P(P(z))|>100, и так далее.
Так что точка из множества Жюлиа J_5 обязательно должна лежать в диске |z|<=4.
|P(z)| >= |z|^2 - |c|;
скажем, для |c|<=5 уже при |z|>4 будет |P(z)|>11, потом |P(P(z))|>100, и так далее.
Так что точка из множества Жюлиа J_5 обязательно должна лежать в диске |z|<=4.
Victor Kleptsyn
М
12:29
Математические байки
Но то же самое можно сказать и про её образ P(z)=z^2+c, поэтому z^2 обязательно содержится в диске с центром в (-5) и радиусом 4. А тогда z содержится в одном из двух прообразов этого диска под действием квадратного корня.
Victor Kleptsyn
М
12:30
Математические байки
А условие |P(P(z))|<=4 выделит в каждом из этих прообразов ещё два прообраза. И вот у нас получаются вложенные объединения топологических дисков, в каждом диске n-го уровня — два диска n+1-го. Так что точки, которые им всем принадлежат — а это и есть множество Жюлиа для такого c — будут канторовым множеством:
Victor Kleptsyn
М
12:33
Математические байки
In reply to this message
Вот тут точка c это примерно 2.7 — а самого множества Жюлиа справа даже не видно, оно "распалось в канторову пыль". Видны только вложенные области — вне первой из них |P(z)| слишком большой, вне следующей (более светлой) |P(P(z))|, и так далее.
Victor Kleptsyn
М
12:33
Математические байки
А вот тут я взял параметр c большим отрицательным:
Victor Kleptsyn
М
12:34
Математические байки
In reply to this message
И это уже совсем привычный вид канторова множества.
Victor Kleptsyn
М
12:38
Математические байки
Так вот, ответ на вопрос про то, а зачем вообще рассматривают множество Мандельброта, и почему там именно итерации z=0, такой:
Теорема. Заполненное множество Жюлиа полинома P_c связно тогда и только тогда, когда критическая точка z=0 этому множеству принадлежит (не убегает на бесконечность). В противном случае оно гомеоморфно канторову множеству.
Теорема. Заполненное множество Жюлиа полинома P_c связно тогда и только тогда, когда критическая точка z=0 этому множеству принадлежит (не убегает на бесконечность). В противном случае оно гомеоморфно канторову множеству.
Victor Kleptsyn
М
12:41
Математические байки
То есть точка z=0 важна тем, что именно в ней производная P_c обращается в ноль; и если её образы убегают на бесконечность — мы получаем примерно такую же картину, как и просто для z^2+с, где c большое. Ну и вот пара примеров —
Victor Kleptsyn
3 June 2020
М
13:32
Математические байки
Сегодня, через четыре с половиной часа :)
Victor Kleptsyn
М
13:32
Математические байки
Н
Непрерывное математическое образование 01.06.2020 13:02:30
https://youtu.be/myq1cr-cKZE
в среду в 18 будет популярная лекция С.К.Смирнова с участием И.В.Ященко и В.А.Клепцына «Зачем нужна математика?» для школьников 7-11 кл., учителей, родителей, всех желающих.
в среду в 18 будет популярная лекция С.К.Смирнова с участием И.В.Ященко и В.А.Клепцына «Зачем нужна математика?» для школьников 7-11 кл., учителей, родителей, всех желающих.
Victor Kleptsyn
5 June 2020
М
14:20
Математические байки
In reply to this message
Уф. Мы это сделали!
Давайте я сюда скопирую скриноштами часть рассказа — мне кажется, получилось действительно интересно.
Начали с исторического экскурса — и первым вспомнили Московский математический папирус (он же папирус Голенищева) — https://ru.wikipedia.org/wiki/%D0%9C%D0%BE%D1%81%D0%BA%D0%BE%D0%B2%D1%81%D0%BA%D0%B8%D0%B9_%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%BF%D0%B0%D0%BF%D0%B8%D1%80%D1%83%D1%81
Давайте я сюда скопирую скриноштами часть рассказа — мне кажется, получилось действительно интересно.
Начали с исторического экскурса — и первым вспомнили Московский математический папирус (он же папирус Голенищева) — https://ru.wikipedia.org/wiki/%D0%9C%D0%BE%D1%81%D0%BA%D0%BE%D0%B2%D1%81%D0%BA%D0%B8%D0%B9_%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%BF%D0%B0%D0%BF%D0%B8%D1%80%D1%83%D1%81
Victor Kleptsyn
14:23
In reply to this message
Задача об объёме усечённой пирамиды с квадратными основаниями, если известны стороны оснований и высота; и в папирусе правильный ответ:
(1/3) h(a^2+b^2+ab)
(1/3) h(a^2+b^2+ab)
Victor Kleptsyn
14:24
А папирусу, как-никак, почти 4 тысячи лет (датировка — около 1850 д.н.э.).
Victor Kleptsyn
14:25
После этого перешли к вавилонской клинописи — к табличке YBC 7289 (https://en.wikipedia.org/wiki/YBC_7289 )
Victor Kleptsyn
14:27
И тут оказывается, что все эти записи вполне можно прочитать. А заодно научиться читать запись чисел клинописью. :)
Victor Kleptsyn
14:29
Берём ту надпись, которая идёт вдоль диагонали квадрата:
Victor Kleptsyn
14:31
"Вертикальный клин" — единица/единицы; "уголок влево" — десяток/десятки.
На диагонали написано "клин — два угла, четыре (слившихся) клина — пять углов, клин — угол", и получается "1 — 24 — 51 — 10".
На диагонали написано "клин — два угла, четыре (слившихся) клина — пять углов, клин — угол", и получается "1 — 24 — 51 — 10".
Victor Kleptsyn
14:33
У вавилонян была шестидесятеричная система (которая нам осталась в минутах и секундах — на которые мы делим и часы, и градусы); давайте посмотрим на это как на "шестидесятеричную" дробь:
Victor Kleptsyn
14:35
И при виде числа 1,4142 — да ещё и с подсказкой в виде диагонали квадрата — становится понятно, о чём речь:
Victor Kleptsyn
14:40
Если точнее, корень из 2 это 1.41421356 — то есть разница записанного значения с правильным примерно в шесть десятимиллионных (и кстати, все три "шестидесятеричные цифры после запятой" — правильные).
То есть на глиняной табличке (которой больше, чем три с половиной тысячи лет) записан корень из двух с вот такой точностью — очевидно превосходящей всё, что могло бы быть нужно для хоть сколько-нибудь практических целей.
То есть на глиняной табличке (которой больше, чем три с половиной тысячи лет) записан корень из двух с вот такой точностью — очевидно превосходящей всё, что могло бы быть нужно для хоть сколько-нибудь практических целей.
Victor Kleptsyn
14:42
In reply to this message
Если вернуться к табличке — то на ней есть ещё две (связанные) надписи. Одна вдоль катета, "три угла" = 30. Или = (1/2) — потому что не было у них отдельной отметки-"запятой".
Victor Kleptsyn
14:43
In reply to this message
Хорошее упражнение — прочитать вторую, идущую вдоль диагонали.
Victor Kleptsyn
14:49
Если делать честно — то полезно взять фото в высоком разрешении — например,
https://upload.wikimedia.org/wikipedia/commons/2/2e/YBC-7289-OBV-labeled.jpg
https://upload.wikimedia.org/wikipedia/commons/2/2e/YBC-7289-OBV-labeled.jpg
Victor Kleptsyn
14:51
- Четыре угла, два клина
Victor Kleptsyn
14:52
= два угла, пять клиньев (в верхней строчке они группируются по три, и рисуются мелко)
Victor Kleptsyn
14:56
- три угла (хотя средний плохо виден), пять клиньев.
Victor Kleptsyn
14:57
Получилось 42; 25; 35. А что это?
Посмотрим на их отношение:
42/30 = 1.4
Учитывая, что 42 (и что-то-там) стоит вдоль диагонали, а 30 вдоль катета, можно начать что-то подозревать :)
Посмотрим на их отношение:
42/30 = 1.4
Учитывая, что 42 (и что-то-там) стоит вдоль диагонали, а 30 вдоль катета, можно начать что-то подозревать :)
Victor Kleptsyn
М
15:25
Математические байки
Можно посчитать честно: найти
42+ (25/60) + 35/3600 = 42.4263(8) ;
после чего поделить на 30 и получить
1.41421296...
42+ (25/60) + 35/3600 = 42.4263(8) ;
после чего поделить на 30 и получить
1.41421296...
Victor Kleptsyn
15:29
А можно чуть-чуть сократить путь: 30=60/2, и деление на 30 числа в шестидесятеричной системе счисления это умножение на 2 + сдвиг на разряд. Поэтому когда мы делим на 30 число
42 ; 25 ; 35,
получается (в старшем и в младшем разрядах происходит "перенос" 1, и остаётся 2*12=24 и 2*5=10 соответственно)
1 ; 2*12=24 ; 2*25+1=51 ; 2*5=10.
1; 24; 51; 10 — где-то мы это число уже видели?
42 ; 25 ; 35,
получается (в старшем и в младшем разрядах происходит "перенос" 1, и остаётся 2*12=24 и 2*5=10 соответственно)
1 ; 2*12=24 ; 2*25+1=51 ; 2*5=10.
1; 24; 51; 10 — где-то мы это число уже видели?
Victor Kleptsyn
15:33
То есть эта пара — это тоже такой же прямоугольный треугольник. Только из-за того, что "запятую" не ставили, неясно — то ли катет 30, а гипотенуза 30\sqrt{2}, то ли катет (1/2), а гипотенуза 1/sqrt{2}=sqrt{2}/2.
(Мне, пожалуй, вторая интерпретация нравится больше.)
(Мне, пожалуй, вторая интерпретация нравится больше.)
Victor Kleptsyn
15:43
Но корень из 2 — это отношение гипотенузы к катету в равнобедренном прямоугольном треугольнике; и его можно найти, даже не зная теоремы Пифагора, а просто из подобия (как раз проведя вторую диагональ в квадрате).
Следующим номером была другая табличка, Plimpton 322 (https://en.wikipedia.org/wiki/Plimpton_322 )
Следующим номером была другая табличка, Plimpton 322 (https://en.wikipedia.org/wiki/Plimpton_322 )
Victor Kleptsyn
15:46
Первый раз я, кажется, о ней прочитал в брошюре Цфасмана и Острика, "Алгебраическая геометрия и теория чисел" — https://www.mccme.ru/free-books/mmmf-lectures/book.8v2.pdf :
Victor Kleptsyn
15:47
Так вот — давайте возьмём в этой таблице первую же строчку. И прочтём числа в двух средних столбцах. Кстати — уже несложно увидеть, что в последнем столбце идут просто порядковые номера: 1, 2, 3, ...
Victor Kleptsyn
15:57
Вот это место под увеличением:
Victor Kleptsyn
15:58
Иными словами —
Victor Kleptsyn
16:00
То есть —
1; 59 и 2; 49.
А давайте переведём их в привычные нам, и попробуем построить прямоугольный треугольник с такими катетом и гипотенузой.
1; 59 и 2; 49.
А давайте переведём их в привычные нам, и попробуем построить прямоугольный треугольник с такими катетом и гипотенузой.
Victor Kleptsyn
16:01
1*60+59 = 119;
2*60+49 = 169.
2*60+49 = 169.
Victor Kleptsyn
16:02
169^2-119^2 можно посчитать честно, а можно как разность квадратов:
50* (119+169) = 50* 288 = 14400.
50* (119+169) = 50* 288 = 14400.
Victor Kleptsyn
16:03
То есть 120^2. Итак, в первой строчке написаны катет и гипотенуза пифагорова треугольника
119^2 + 120^2 = 169^2
119^2 + 120^2 = 169^2
Victor Kleptsyn
7 June 2020
М
16:40
Математические байки
Давайте, наверное, закончим с этой табличкой. Посмотрим теперь на 11-ю строчку:
Victor Kleptsyn
16:44
Гипотенуза записана как "клин — уголок, пять клиньев", то есть "1; 15". Это даёт нам
60*1+15=75.
У катета явно видно тоже пять клиньев на конце; то, что перед ними, читается хуже, но там будет 45 (что можно увидеть, перебрав варианты).
60*1+15=75.
У катета явно видно тоже пять клиньев на конце; то, что перед ними, читается хуже, но там будет 45 (что можно увидеть, перебрав варианты).
Victor Kleptsyn
16:48
45 и 75 — не взаимно просты (единственная или почти единственная такая строчка во всей таблице!); если вынести 15 за скобки, то видим
45=3*15,
75=5*15,
то есть это как раз самый классический пифагоров треугольник 3-4-5!
45=3*15,
75=5*15,
то есть это как раз самый классический пифагоров треугольник 3-4-5!
Victor Kleptsyn
16:49
Давайте теперь расшифруем запись в первом столбце:
Victor Kleptsyn
16:59
Тут написано 33; 45. Ну и давайте угадаем, что это запись "маленького" числа, а не "большого". То есть мы пишем
33/60 + 45/(60*60) =
11/20 + 1/80 =
45/80 =
9/16
33/60 + 45/(60*60) =
11/20 + 1/80 =
45/80 =
9/16
Victor Kleptsyn
16:59
И дробь 9/16 для треугольника 3-4-5 наводит на мысли, что это 3^2/4^2, квадрат тангенса. Так вот, всё так и есть!
Victor Kleptsyn
17:07
В первом столбце записан то ли квадрат тангенса — то ли, если к этим числам слева добавить вертикальный клин (то есть единицу), квадрат секанса:
Victor Kleptsyn
17:09
Вот расшифрованная версия из всё той же брошюры Цфасмана-Острика:
Victor Kleptsyn
17:11
Кстати — обратите внимание, что по первому столбцу (иными словами, по углу) треугольники упорядочены; а ещё, что в этой табличке вполне есть несколько опечаток (частью пустяковых, но частью нет).
Victor Kleptsyn
17:19
В заключение вавилонской темы — мне тут коллеги напомнили о первом фильме, снятом на вавилонском диалекте аккадского:
https://nplus1.ru/news/2018/12/03/poor-man-of-nippur
(или https://www.youtube.com/watch?v=pxYoFlnJLoE )
https://nplus1.ru/news/2018/12/03/poor-man-of-nippur
(или https://www.youtube.com/watch?v=pxYoFlnJLoE )
Victor Kleptsyn
17:20
Открывающие титры сразу помогают настроиться:
Victor Kleptsyn
17:25
И в заключение исторического экскурса — в лекцию это не вошло, но мне хочется вспомнить Алкуина из Йорка и его задачи для молодёжи —
https://ru.wikipedia.org/wiki/Propositiones_ad_Acuendos_Juvenes
https://ru.wikipedia.org/wiki/Propositiones_ad_Acuendos_Juvenes
Victor Kleptsyn
17:28
Я помню, как я удивился, когда об этом узнал: больше тысячи лет назад уже были совершенно "кружковские" задачи:
волк, коза и капуста;
переправа трёх ревнивых мужей с жёнами;
и даже(!) сумма чисел от 1 до 100.
волк, коза и капуста;
переправа трёх ревнивых мужей с жёнами;
и даже(!) сумма чисел от 1 до 100.
Victor Kleptsyn
17:37
И я сейчас прервусь на (начинающуюся через час) другую лекцию. В качестве спойлера — один слайд из неё:
Victor Kleptsyn
17:38
Слева апельсины сложили квадратной решёткой в нижнем слое. Потом положили второй слой в получившиеся дырки, третий слой в дырки второго, и так далее.
Victor Kleptsyn
17:39
По центру — в нижнем слое начали с "треугольной" упаковки. Она плотнее, зато апельсины второго слоя пришлось положить выше, и занять получается только половину "дырок".
Victor Kleptsyn
17:42
Справа — то, что называется кубической гранецентрированной (cubic face-centered) решёткой: центры шаров образуют кубическую решётку, в которой добавлено по ещё по одному в центр каждой грани каждого куба (а синие отрезки это кратчайшие расстояния для упаковки).
Victor Kleptsyn
17:42
Вопрос: какая из них плотнее?
Victor Kleptsyn
17:45
Какая упаковка плотнее
Final results
- С квадратной упаковкой в слое 34 votes
- С треугольной упаковкой в слое 88 votes
- Кубическая гранецентрированная 97 votes
- *** **** * ** ** ******** 115 votes, chosen vote
334 votes
Victor Kleptsyn
9 June 2020
М
19:40
Математические байки
In reply to this message
Правильный ответ:
это одна и та же упаковка!
это одна и та же упаковка!
Victor Kleptsyn
19:42
Вот одинаково расположенные шесть шаров на первых двух картинках:
Victor Kleptsyn
19:43
Или же можно посмотреть на "боковую грань" квадратно-упакованных апельсинов — и увидеть, что они там упакованы "треугольным" образом:
Victor Kleptsyn
19:46
Наконец, в одной вертикальной плоскости cfc-упаковки центры образуют как раз квадратную сетку — только с поворотом на 45 градусов:
Victor Kleptsyn
19:48
А точки в центрах граней других направлений как раз образуют решётку "со сдвигом".
Victor Kleptsyn
19:52
В этой упаковке, кстати, реализуется контактное число в размерности 3 — каждого шара касаются ровно 12 других (в варианте треугольной упаковки — 6 в том же слое, 3 сверху и 3 снизу). А вот посвящённый вопросу о контактном числе мультфильм "Математических Этюдов" — https://www.etudes.ru/ru/etudes/contact-number/
Victor Kleptsyn
М
19:52
Математические байки
Г
Геометрия-канал 28.05.2020 23:11:02
344. Можно ли расположить в пространстве 13 одинаковых шариков так, чтобы они не пересекались и при этом 12 шариков касались одного.
#задача
#задача
Victor Kleptsyn
М
20:01
Математические байки
In reply to this message
Собственно, интересно, что у задачи выше есть очень много решений: например, вместо того, чтобы выделять часть большой упаковки, можно разместить эти 12 шаров в вершинах правильного икосаэдра. И — их можно катать, не отрывая от поверхности внутреннего шара И даже реализовывать нетривиальные их перестановки — то ли чётные, то ли вообще все; одну такую перестановку — цикл длины 5 — показывают в фильме (2:50-3:10), а всех таких циклов хватит, чтобы породить все чётные перестановки.
Victor Kleptsyn
10 June 2020
М
12:58
Математические байки
In reply to this message
Давайте я ещё поделюсь вот таким фото из — тоже посвящённого решёткам и упаковкам, но более короткого — рассказа Жени Смирнова, https://www.youtube.com/watch?v=AHP3jPJ2T7k&feature=youtu.be :
Victor Kleptsyn
13:04
In reply to this message
Видно, что на одной грани ядра сложены треугольным образом, а на другой — квадратным.
Да, про ядра: четыре года назад Константин Новосёлов (нобелевская премия за графен) читал лекцию на ВсОШ-2016 по математике. Он рассказывал много чего — но ещё мне запомнилась забавная история: графит был стратегическим сырьём задолго до атомной бомбы. Потому что применялся при отливке пушечных ядер!
Да, про ядра: четыре года назад Константин Новосёлов (нобелевская премия за графен) читал лекцию на ВсОШ-2016 по математике. Он рассказывал много чего — но ещё мне запомнилась забавная история: графит был стратегическим сырьём задолго до атомной бомбы. Потому что применялся при отливке пушечных ядер!
Victor Kleptsyn
13:04
Victor Kleptsyn
13:09
In reply to this message
Да, собственно, эта лекция (которую я читал в Computer Science Club — https://compsciclub.ru/courses/csseminar/2020-spring/classes/5816/ ) была как раз посвящена решёткам, упаковкам шаров и кодам — и мне хочется несколько кусочков оттуда пересказать и тут.
Victor Kleptsyn
13:12
Первый кусочек, простой, но меня в своё время сильно удививший. Возьмём квадрат со стороной 2, поделим на четыре равных квадрата, впишем в каждый по кругу единичного диаметра:
Victor Kleptsyn
13:13
Теперь поместим в центр квадрата маленький круг, касающийся этих четырёх:
Victor Kleptsyn
13:14
И то же самое сделаем в размерности 3 (восемь единичных шаров и маленький шарик в центре, их всех касающийся), и продолжим во всех старших размерностях.
Вопрос: чему равен диаметр центрального шарика? И как он меняется с ростом размерности n?
Вопрос: чему равен диаметр центрального шарика? И как он меняется с ростом размерности n?
Victor Kleptsyn
13:19
In reply to this message
Удивительный ответ — начиная с размерности 5, центральный шарик становится больше остальных. А начиная с размерности 10, он пересекает границу исходного куба с ребром 2!
Правда, при взгляде на двумерную картинку в это не верится?
Правда, при взгляде на двумерную картинку в это не верится?
Victor Kleptsyn
13:22
Выкладка тут, на самом деле, очень простая. Сначала посмотрим на центры исходных шаров — они находятся в вершинах единичного куба. Диагональ этого куба равна — по теореме Пифагора — корню из n (ибо корень из 1^2+...+1^2).
Victor Kleptsyn
13:23
Из этого корня из n единица уходит на два радиуса=диаметр двух противоположных шаров. И остаётся диаметр центрального шара — равный, тем самым,
\sqrt{n}-1.
\sqrt{n}-1.
Victor Kleptsyn
13:26
In reply to this message
При n>4 этот диаметр больше 1, а при n>9 — больше 2. И ответ на вопрос, "а как же он за границу куба вылезет" — "по центру грани, где ему не помешают".
Собственно, двумерную картинку выше можно мысленно себе представить как трёхмерную, на которую мы смотрим с одной из граней — и там понятно, что центральный шарик будет уже больше (а точки касания с четырьмя видимыми нам шарами будут на невидимой нам их части).
Собственно, двумерную картинку выше можно мысленно себе представить как трёхмерную, на которую мы смотрим с одной из граней — и там понятно, что центральный шарик будет уже больше (а точки касания с четырьмя видимыми нам шарами будут на невидимой нам их части).
Victor Kleptsyn
13:28
Но самое интересное — это что при n=4 центральный шарик оказывается равным остальным. И это позволяет сделать вот такую красивую упаковку шаров в четырёхмерном пространстве: сначала упаковываем "гиперкубически" (так, чтобы центры образовывали решётку Z^4), а потом добавляем ещё по одному такому же шару в центр каждого гиперкуба — там как раз для него есть место.
Victor Kleptsyn
13:29
Получается шахматная решётка.
Victor Kleptsyn
13:31
Вопрос: а сколько и каких шаров в такой упаковке касаются одного фиксированного?
Victor Kleptsyn
М
16:01
Математические байки
Ответ — 24.
А именно — 2^4=16 шаров в вершинах гиперкуба будут касаться центрального шара. Но ещё его будут касаться центральные шары из 2*4=8 соседних гиперкубов!
Поэтому и 16+8=24.
Если говорить на языке кратчайших векторов решётки, то первые соответствуют 16 расстановкам знаков для векторов (±1/2, ±1/2, ±1/2, ±1/2), а вторые — 8 векторам вида "±1 по одной координате, 0 по остальным".
А именно — 2^4=16 шаров в вершинах гиперкуба будут касаться центрального шара. Но ещё его будут касаться центральные шары из 2*4=8 соседних гиперкубов!
Поэтому и 16+8=24.
Если говорить на языке кратчайших векторов решётки, то первые соответствуют 16 расстановкам знаков для векторов (±1/2, ±1/2, ±1/2, ±1/2), а вторые — 8 векторам вида "±1 по одной координате, 0 по остальным".
Victor Kleptsyn
16:06
И эти 24 центра образуют правильный многогранник в четырёхмерном пространстве — один из трёх нетривиальных!
В любой размерности есть правильные многогранники — (гипер)куб, симплекс (аналог тетраэдра) и "гипероктаэдр" (двойственный к кубу). Но в размерностях, больших 4, больше ничего нет.
В размерности 3 есть ещё двойственные друг другу додекаэдр и икосаэдр.
А в размерности 4 есть ещё три нетривиальных правильных многогранника — тот самый (самодвойственный) 24-вершинник, и двойственные друг другу 120- и 600-вершинники.
В любой размерности есть правильные многогранники — (гипер)куб, симплекс (аналог тетраэдра) и "гипероктаэдр" (двойственный к кубу). Но в размерностях, больших 4, больше ничего нет.
В размерности 3 есть ещё двойственные друг другу додекаэдр и икосаэдр.
А в размерности 4 есть ещё три нетривиальных правильных многогранника — тот самый (самодвойственный) 24-вершинник, и двойственные друг другу 120- и 600-вершинники.
Victor Kleptsyn
16:07
Вот так этот 24-вершинник выглядит:
Victor Kleptsyn
16:10
Такая картинка получается, если его сначала "раздуть" до трёхмерной сферы (вложенной в R^4) — а потом стереографически спроецировать эту сферу на R^3.
И это кадр из фильма "Dimensions" (http://dimensions-math.org/Dim_RU.htm ), который сделали в своё время Etienne Ghys (Этьен Жис), Jos Leys и Aurelien Alvarez — состоящий из девяти 13-минутных глав.
И это кадр из фильма "Dimensions" (http://dimensions-math.org/Dim_RU.htm ), который сделали в своё время Etienne Ghys (Этьен Жис), Jos Leys и Aurelien Alvarez — состоящий из девяти 13-минутных глав.
Victor Kleptsyn
16:15
Самые красивые картинки правильных 4-мерных многогранников появляются в четвёртой главе, вот тут — https://youtu.be/74yIvy0F1bk?t=6m40s .
А ещё два года назад Женя Смирнов читал в ЛШСМ курс про правильные многогранники —
https://www.mccme.ru/dubna/2018/courses/esmirnov.html — и я очень советую текст его записок:
http://www.mccme.ru/free-books/dubna/smirnov-reflections-v2.pdf
А ещё два года назад Женя Смирнов читал в ЛШСМ курс про правильные многогранники —
https://www.mccme.ru/dubna/2018/courses/esmirnov.html — и я очень советую текст его записок:
http://www.mccme.ru/free-books/dubna/smirnov-reflections-v2.pdf
Victor Kleptsyn
16:16
Связывая разные кусочки — вот одно упражнение из середины (глава "2 1/2", почти "9 3/4") —
Victor Kleptsyn
11 June 2020
М
10:59
Математические байки
Н
Непрерывное математическое образование 11.06.2020 10:42:07
12 июня — традиционный день Арнольда: Арнольдовская лекция А.М.Вершика и лекция Арнольдовского стипендиата Романа Крутовского
https://math.hse.ru/announcements/371576993.html
https://math.hse.ru/announcements/371576993.html
Victor Kleptsyn
М
13:04
Математические байки
О, вот эта задача совершенно замечательная — и сама по себе, и ещё больше связанной с ней историей (см. послесловие):
Victor Kleptsyn
М
13:04
Математические байки
E
Elementy.ru 10.06.2020 19:41:30
Древнее древних греков
Даны соединенные вместе фрагменты текста, найденного в 1952 году на глиняной табличке в городе Пилосе, и их условные транскрипции в перепутанном порядке:
1. dipa mewijo tirijowe
2. dipae mezoe tiriowee
3. dipa mewijo anowe
4. dipa mewijo qetorowe
5. tiripode ajkeu keresijo weke
6. tiripo eme pode owowe
7. dipa mezoe qetorowe
Выделите в тексте фрагменты и найдите соответствия. Попробуйте понять, как переводятся слова: anowe, tiripo, qetorowe, dipa, tirijowe, dipae, tiripode.
Из послесловия вы узнаете, что это за табличка и какую роль она сыграла в расшифровке древней микенской письменности.
elementy.ru/link/t/Pylos
Даны соединенные вместе фрагменты текста, найденного в 1952 году на глиняной табличке в городе Пилосе, и их условные транскрипции в перепутанном порядке:
1. dipa mewijo tirijowe
2. dipae mezoe tiriowee
3. dipa mewijo anowe
4. dipa mewijo qetorowe
5. tiripode ajkeu keresijo weke
6. tiripo eme pode owowe
7. dipa mezoe qetorowe
Выделите в тексте фрагменты и найдите соответствия. Попробуйте понять, как переводятся слова: anowe, tiripo, qetorowe, dipa, tirijowe, dipae, tiripode.
Из послесловия вы узнаете, что это за табличка и какую роль она сыграла в расшифровке древней микенской письменности.
elementy.ru/link/t/Pylos
Victor Kleptsyn
12 June 2020
М
15:05
Математические байки
Начинается лекция А. М. Вершика на дне Арнольда —
Victor Kleptsyn
13 June 2020
М
15:30
Математические байки
In reply to this message
Давайте продолжим — и раз уж у нас всплыли правильные многогранники, то тут есть ответвление, которое нельзя не упомянуть: давайте построим два оставшихся четырёхмерных правильных многогранника. Точнее, построим 120-вершинник, а 120-гранник с 600 вершинами будет просто двойственным к нему. И для этого — посмотрим, какая связь между кватернионами и вращениями трёхмерного пространства.
Victor Kleptsyn
15:33
Про кватернионы есть замечательная книга В. И. Арнольда, "Геометрия комплексных чисел, кватернионов и спинов" — https://www.mccme.ru/free-books/izdano/2002/VIA-kvatern.pdf — которую мне хочется всячески порекламировать (а мой рассказ тут близко следует ей — а точнее, той лекции В.И.А. на малом мехмате, из которой она получилась).
Victor Kleptsyn
15:37
Так вот: у нас есть кватернионы, числа вида a+bi+cj+dk с некоммутативным умножением:
Victor Kleptsyn
15:38
И как и в комплексных числах, в них есть сопряжение, изменяющее знак у всех трёх "мнимых единиц" i, j и k:
Victor Kleptsyn
15:39
Но в отличие от комплексных чисел, в кватернионах сопряжение изменяет порядок сомножителей:
Victor Kleptsyn
15:43
Это несложно проверить (собственно, это как раз и есть антикоммутативность произведения на разных мнимых единицах); а произведение z*conj(z) это квадрат длины z как вектора в R^4.
Собственно, вещественная часть сразу видно, что будет равна a^2+b^2+c^2+d^2, а мнимые компоненты можно или проверить, что сократятся, или сказать, что z*conj(z) сохраняется сопряжением:
Собственно, вещественная часть сразу видно, что будет равна a^2+b^2+c^2+d^2, а мнимые компоненты можно или проверить, что сократятся, или сказать, что z*conj(z) сохраняется сопряжением:
Victor Kleptsyn
15:44
А, значит, это произведение чисто вещественно. Что более нетривиально — модуль произведения, как и в комплексных числах, оказывается равен произведению модулей:
Victor Kleptsyn
15:47
В качестве шага в сторону — отсюда получается, что если два числа представимы в виде суммы четырёх квадратов, то представимо в виде суммы четырёх квадратов и их произведение. Поэтому теорему Лагранжа о том, что в виде суммы четырёх квадратов представляется любое натуральное число, достаточно доказывать лишь для простых чисел.
Victor Kleptsyn
15:53
Но давайте вернёмся к кватернионам и к их младшим братьям — комплексным числам. Если у нас есть комплексное число q, равное 1 по модулю, то можно рассмотреть умножение на q как отображение комплексной плоскости в себя,
M_q : z-> qz.
И поскольку |qz|=|q|*|z| — это движение. Причём сохраняющее ноль, и несложно (например, по непрерывности) увидеть, что это поворот. На угол, равный аргументу q — потому что 1 переходит в q. Поэтому при перемножении комплексных чисел аргументы складываются — и формулы для косинуса и синуса суммы это на самом деле одна формула,
M_q : z-> qz.
И поскольку |qz|=|q|*|z| — это движение. Причём сохраняющее ноль, и несложно (например, по непрерывности) увидеть, что это поворот. На угол, равный аргументу q — потому что 1 переходит в q. Поэтому при перемножении комплексных чисел аргументы складываются — и формулы для косинуса и синуса суммы это на самом деле одна формула,
Victor Kleptsyn
15:54
— только в ней раскрыты скобки. В частности, тот самый "минус" для косинуса суммы,
Victor Kleptsyn
15:55
это i^2=-1.
Victor Kleptsyn
15:56
Но это совсем стандартные вещи — а вернёмся к кватернионам. Они некоммутативные — и если есть кватернион q с |q|=1, то можно умножать кватернионы на q как слева, так и справа:
Victor Kleptsyn
15:57
И оба этих умножения будут движениями четырёхмерного пространства R^4=H, потому что |qz|=|zq|=|z|.
Victor Kleptsyn
15:58
Да, кстати. Точно так же, как единичная окружность на комплексной плоскости является группой по умножению — точно так же (уже некоммутативной!) группой по умножению будет трёхмерная сфера S^3 кватернионов единичной длины.
Victor Kleptsyn
15:59
Так вот: давайте возьмём такой "единичный" кватернион q и умножим на него слева — и на обратный к нему \conj(q)=q^{-1} справа:
Victor Kleptsyn
16:00
Во-первых, получилось движение четырёхмерного пространства (потому что и по отдельности эти умножения были движениями).
Victor Kleptsyn
16:00
Во-вторых, единицу — а значит, и всю вещественную прямую — оно оставляет на месте.
Victor Kleptsyn
16:01
И значит, оставляет на месте как множество и трёхмерное пространство чисто мнимых кватернионов — ортогональное дополнение к вещественной прямой.
Victor Kleptsyn
16:02
То есть всякому кватерниону единичной длины q сопоставляется вращение трёхмерного пространства {bi+cj+dk} чисто мнимых кватернионов.
Victor Kleptsyn
16:04
Причём это отображение почти взаимно-однозначно — единственное, что в q можно поменять, это знак. (Что не очень сложно проверить.)
Поэтому вращение трёхмерного пространства кодируется кватернионом единичной длины, заданным однозначно с точностью до знака. Иными словами, группа S^3 двулистно накрывает группу SO(3).
Поэтому вращение трёхмерного пространства кодируется кватернионом единичной длины, заданным однозначно с точностью до знака. Иными словами, группа S^3 двулистно накрывает группу SO(3).
Victor Kleptsyn
16:05
И — вот такое вполне применяется для задания/хранения ориентации что для спутников, что в видеоиграх.
В отличие от углов Эйлера — "курс, тангаж, крен" — тут нет направления, где будет "деление на ноль" (у летящего вертикально вверх истребителя курса нет), легко считается композиция (перемножить кватернионы, и вся недолга).
В отличие от матриц — по крайней мере, ошибки округления (если экономить память) не уведут нас с множества ортогональных матриц, и не будет вопроса, "как бы получше выбрать ближайшую ортогональную матрицу", когда ошибки накопятся.
В отличие от углов Эйлера — "курс, тангаж, крен" — тут нет направления, где будет "деление на ноль" (у летящего вертикально вверх истребителя курса нет), легко считается композиция (перемножить кватернионы, и вся недолга).
В отличие от матриц — по крайней мере, ошибки округления (если экономить память) не уведут нас с множества ортогональных матриц, и не будет вопроса, "как бы получше выбрать ближайшую ортогональную матрицу", когда ошибки накопятся.
Victor Kleptsyn
16:08
Кстати — вот если умножать слева и справа на разные кватернионы (и справа — на обратный),
Victor Kleptsyn
16:08
то получается гомоморфизм
S^3 x S^3 -> SO(4),
потому что умножения слева и справа коммутируют.
S^3 x S^3 -> SO(4),
потому что умножения слева и справа коммутируют.
Victor Kleptsyn
16:09
И несложно увидеть, что образ у него всё, а ядро — это только (1,1) и (-1,-1). И вот ещё одно двулистное накрытие (а заодно разложение алгебры Ли so(4) в прямую сумму двух копий so(3)).
Victor Kleptsyn
16:11
Так вот, вернёмся наконец к нашим четырёхмерным правильным многогранникам. Чтобы задать многогранник, достаточно задать его вершины — и их естественно выбирать на той самой единичной сфере в R^4 = H.
Victor Kleptsyn
16:14
Так вот — давайте возьмём группу вращений правильного тетраэдра. Она действует чётными перестановками его вершин — поэтому в ней 12 элементов. (Кстати, хорошее упражнение это перечислить их, ничего не забыв!)
Victor Kleptsyn
16:15
И давайте возьмём у неё полный прообраз при отображении S^3->SO(3). Получим 24 точки на единичной сфере в четырёхмерном пространстве. И мы их уже видели:
Victor Kleptsyn
16:15
(из той же брошюры Жени Смирнова)
Victor Kleptsyn
16:16
А теперь возьмём вместо тетраэдра — икосаэдр или додекаэдр, благо, из-за их двойственности группа вращений у них одна и та же.
Victor Kleptsyn
16:17
Группа вращений у додекаэдра состоит из 12*5=60 элементов: любую грань можно перевести в любую, а дальше есть 5 вариантов поворотов.
Victor Kleptsyn
16:18
Собственно, как группа она изоморфна A_5, группе чётных перестановок 5 элементов, и есть красивый ответ на вопрос "а какие 5 элементов переставляются": это 5 вписанных в додекаэдр кубов.
Victor Kleptsyn
16:19
Вот тут изображён один такой куб —
https://commons.wikimedia.org/wiki/File:Cube_in_dodecahedron.png — а любая диагональ в грани дальше однозначно достраивается, поэтому их 5.
https://commons.wikimedia.org/wiki/File:Cube_in_dodecahedron.png — а любая диагональ в грани дальше однозначно достраивается, поэтому их 5.
Victor Kleptsyn
16:21
(Кстати, это ещё и способ рисовать додекаэдр — сначала нарисовать куб, а потом на каждую его грань приделать по согласованной "крыше дома")
Victor Kleptsyn
16:22
Ну так вот — у нас есть замечательная группа из 60 вращений. Давайте у неё возьмём прообраз в S^3 — получится очень симметричный набор из 120 точек. Это и есть 120 вершин правильного четырёхмерного 600-гранника!
Victor Kleptsyn
16:24
In reply to this message
Наконец, двойственный к нему — 120-гранник; его изображение — один из моих любимых кадров фильма Жиса, Лейса и Альвареса, который я тут уже упоминал:
Victor Kleptsyn
М
17:36
Математические байки
In reply to this message
Кстати: если у нас на трёхмерной сфере задана функция, которую мы хотим проинтегрировать (или, что то же самое с точностью до множителя, усреднить), можно приблизить её среднее средним арифметическим по удачно расположенным точкам. Так вот — усреднение по этим 120 вершинам оказывается очень точным приближением: http://mi.mathnet.ru/mz863 (да, а Андреев тут — тот самый, который "Математические этюды").
Victor Kleptsyn
17:42
Да, последнее про кватернионы — кусочек из "Математической составляющей", https://book.etudes.ru/toc/quaternions/
(кстати, автор этой главы — летавший космонавт: https://ru.wikipedia.org/wiki/%D0%91%D0%B0%D1%82%D1%83%D1%80%D0%B8%D0%BD,_%D0%AE%D1%80%D0%B8%D0%B9_%D0%9C%D0%B8%D1%85%D0%B0%D0%B9%D0%BB%D0%BE%D0%B2%D0%B8%D1%87 )
(кстати, автор этой главы — летавший космонавт: https://ru.wikipedia.org/wiki/%D0%91%D0%B0%D1%82%D1%83%D1%80%D0%B8%D0%BD,_%D0%AE%D1%80%D0%B8%D0%B9_%D0%9C%D0%B8%D1%85%D0%B0%D0%B9%D0%BB%D0%BE%D0%B2%D0%B8%D1%87 )
Victor Kleptsyn
17:44
А я возвращаюсь к обещанному построению замечательной решётки E_8, которая даёт плотнейшую упаковку шаров в 8-мерном пространстве, а также максимизирует контактное число, ну и замечательна далеко не только этим.
Victor Kleptsyn
17:53
Если мы уже знаем, что центры шаров будут размещены в узлах решётки, то количество их обратно пропорционально объёму фундаментального параллелепипеда решётки (его ещё называют кообъёмом ), потому что на каждый фундаментальный параллелепипед приходится по одному центру (в фиксированном его углу):
Victor Kleptsyn
17:57
С другой стороны, объём одного шара пропорционален n-й степени его радиуса (или диаметра), а максимальный диаметр, который можно взять, равен наименьшему расстоянию d_{min} между узлами решётки. Поэтому плотность упаковки, получающейся из решётки, пропорциональна отношению n-й степени этого диаметра к кообъёму:
Victor Kleptsyn
18:00
И естественно, что получается величина, инвариантная относительно гомотетии. Поэтому можно либо ограничиться решётками, у которых d_{min}=1, и минимизировать кообъём, либо наоборот, ограничиться решётками с единичным кообъёмом, и максимизировать d_{min}.
Так вот, давайте пока примем именно второй подход. Так, если мы возьмём просто кубическую упаковку Z^8, то d_{min} будет равен 1.
Так вот, давайте пока примем именно второй подход. Так, если мы возьмём просто кубическую упаковку Z^8, то d_{min} будет равен 1.
Victor Kleptsyn
18:02
Для оптимальной решётки наименьшее расстояние будет в \sqrt{2} раз больше — так что упаковка получится в \sqrt{2}^8=2^4=16 раз более плотной!
Victor Kleptsyn
18:04
Так вот — давайте эту решётку построим. Для этого сначала выделим в Z^8 подрешётку \Lambda индекса 2 — вектора с чётной суммой цифр. При этом кообъём удвоится (потому что мы оставили только половину узлов)
Victor Kleptsyn
18:05
А теперь добавим к этой решётке её же, сдвинутую на вектор
v=(1/2,1/2,...,1/2).
v=(1/2,1/2,...,1/2).
Victor Kleptsyn
18:06
Мы и получаем искомую решётку:
Victor Kleptsyn
18:06
Интересно, что эта решётка будет чётной : квадраты длин всех её векторов чётные.
Victor Kleptsyn
18:08
Кстати, хорошее (и простое) упражнение: проверить, что (любая) чётная решётка автоматически является целой : скалярные произведения любых двух её векторов целые.
Victor Kleptsyn
18:11
In reply to this message
Проверить это несложно: <v,v>=8*(1/4)=2, в \Lambda тоже все квадраты чётные (потому что сумма квадратов целых чисел сравнима с их суммой и потому по определению \Lambda чётна). Наконец, скалярное произведение v с любым вектором u из \Lambda целое, а в формуле для квадрата суммы есть двойка:
<kv+u,kv+u>=k^2 <v,v> + <u,u> + 2k <u,v>.
<kv+u,kv+u>=k^2 <v,v> + <u,u> + 2k <u,v>.
Victor Kleptsyn
18:11
А значит, наименьшая возможная длина вектора из решётки E_8 — это корень из 2!
Victor Kleptsyn
18:12
Ибо меньшё 2 чётных чисел нет.
Victor Kleptsyn
18:20
Кстати — чётные решётки с кообъёмом 1 бывают только в пространствах, размерность которых делится на 8.
И это нетривиальное утверждение, которое доказывается через модулярные формы — о чём я точно скажу, но не прямо сейчас.
И это нетривиальное утверждение, которое доказывается через модулярные формы — о чём я точно скажу, но не прямо сейчас.
Victor Kleptsyn
18:30
Второй способ построить решётку E_8 связан с кодами, исправляющими ошибки. (Да, Александр Шень читал целый курс об них — https://www.youtube.com/watch?v=DNCpIo1Gjco — но мне понадобится из этого довольно немного.)
Victor Kleptsyn
18:30
А именно — представим себе, что мы передаём сигнал из 0 и 1 по каналу, где время от времени возникают помехи, и в результате время от времени вместо 0 приходит 1 или наоборот. Как с этим бороться?
Victor Kleptsyn
18:38
Давайте объединим передаваемые биты в блоки. И пусть блок может быть не любым — а только одним из разрешённых кодовых слов, которые мы постараемся сделать как можно более непохожими друг на друга. Тогда, даже если где-то при передаче произойдёт ошибка — мы сможем её заметить, а может быть, даже исправить.
Victor Kleptsyn
18:38
Например, можно просто дописать к блоку из n битов дополнительный бит контроля чётности, всегда равный сумме предыдущих по модулю 2.
Victor Kleptsyn
18:39
Тогда, если при передаче произойдёт одна ошибка, мы не сможем сказать, где она произошла, но — по крайней мере, мы её заметим (и сможем потом "переспросить" у отправителя этот блок).
Victor Kleptsyn
18:42
Можно просто каждый бит повторять по 3 раза: код {000,111} позволяет не только заметить, но и исправить одну ошибку. Но — скорость канала при этом падает втрое.
Victor Kleptsyn
18:48
А нельзя ли исправить одну ошибку в блоке с меньшим падением скорости? Можно, и самый простой такой код это код Хэмминга.
Victor Kleptsyn
18:50
Да — такие коды (передаваемая информация группируется в блоки фиксированного размера) называются блочными. Ещё — если мы захотим работать с блоками большого размера, то у нас должен получиться большой "алфавит". В общей ситуации его даже просто хранить может быть не очень удобно. Поэтому — есть такой удобный подкласс блочных кодов, линейные коды. У которых разрешённый набор блоков это линейное подпространство в F_2^n.
Victor Kleptsyn
18:54
Матрица, в которую (по строкам — так удобнее) записан базис этого подпространства, называется порождающей матрицей линейного кода.
Если применить метод Гаусса, перевыбрав базис, то можно привести порождающую матрицу к виду
M=(Id_k | что-то);
это будет означать, что первые k бит это собственно передаваемая информация, а оставшиеся n-k это своеобразная "контрольная сумма".
Если применить метод Гаусса, перевыбрав базис, то можно привести порождающую матрицу к виду
M=(Id_k | что-то);
это будет означать, что первые k бит это собственно передаваемая информация, а оставшиеся n-k это своеобразная "контрольная сумма".
Victor Kleptsyn
18:55
Так вот, код Хэмминга — линейный блочный код с кодовым расстоянием (т.е. наименьшим расстоянием между элементами кода), равным 3, и потому позволяет исправить одну ошибку. И вот его порождающая матрица:
Victor Kleptsyn
18:58
Этот код позволяет в блоке длины 7 передать 4 бита, и при этом исправляет одну ошибку.
Стандартный фокус, который с его помощью делается — игра "загадай число от 1 до 15 и ответь на 7 вопросов; отвечая, можно один раз соврать, а я всё равно угадаю загаданное число".
Стандартный фокус, который с его помощью делается — игра "загадай число от 1 до 15 и ответь на 7 вопросов; отвечая, можно один раз соврать, а я всё равно угадаю загаданное число".
Victor Kleptsyn
19:05
Вопросы, разумеется, в виде заранее подготовленных карточек — "есть ли твоё число на этой карточке".
У нас в Ренне обычно среди прочего бывает и такое на стенде математиков на днях науки; дети радостно пользуются разрешением соврать — я помню буквально два-три случая, когда при показе этого фокуса на все вопросы отвечали честно. :)
(Вот тут есть реализация этого на смайликах — http://xavier.toonywood.org/popularization/applets/hamming.html — правда, с вопросами по-французски)
У нас в Ренне обычно среди прочего бывает и такое на стенде математиков на днях науки; дети радостно пользуются разрешением соврать — я помню буквально два-три случая, когда при показе этого фокуса на все вопросы отвечали честно. :)
(Вот тут есть реализация этого на смайликах — http://xavier.toonywood.org/popularization/applets/hamming.html — правда, с вопросами по-французски)
Victor Kleptsyn
19:15
Да, и если уж об этом зашла речь, давайте я скажу, что проверочной матрицей кода называется матрица, где по строчкам записан базис ортогонального дополнения к коду. Она проверочная — потому что если её умножить на правильное сообщение, то будет вектор из одних нулей.
Несложно увидеть, что проверочная матрица к коду с порождающей матрицей
(Id_k | A)
это матрица
(A^* | Id_{n-k}).
В частности, для кода Хэмминга проверочной матрицей будет
Несложно увидеть, что проверочная матрица к коду с порождающей матрицей
(Id_k | A)
это матрица
(A^* | Id_{n-k}).
В частности, для кода Хэмминга проверочной матрицей будет
Victor Kleptsyn
19:16
Отсюда, во-первых, видно, что кодовое расстояние действительно не меньше 3: все столбцы разные и ненулевые, поэтому сумма mod 2 никаких <=2 не будет нулевой.
Victor Kleptsyn
19:17
А во-вторых, видно, как показывать фокус: нужно просто иметь такую матрицу записанной, складывать по модулю 2 те столбцы, про которые был ответ "да" — и сумма будет равна тому столбцу, в котором отвечающий соврал. Или нулевому столбцу, если он такой возможностью не воспользовался.
Victor Kleptsyn
19:18
Но давайте вернёмся к коду Хэмминга, и усилим его, добавив бит контроля чётности:
Victor Kleptsyn
19:20
Скорость передачи упала ровно вдвое — мы теперь передаём 4 бита за блок длиной 8. Зато кодовое расстояние возросло до 4, поэтому мы можем не только исправить одну ошибку, но и обнаружить (хоть и не исправить) две.
Victor Kleptsyn
19:22
И кстати — несколько более сложные, но аналогичные коды реально применялись для связи с далёкими зондами:
Victor Kleptsyn
19:23
Victor Kleptsyn
19:25
In reply to this message
Так вот, расширенный код Хэмминга обладает двумя замечательными свойствами: он дважды чётен (вес, то есть число единиц в любом его элементе, делится на 4; терминология традиционная), и унимодулярен: размерность у него равна половине размерности всего пространства.
Victor Kleptsyn
19:27
Давайте теперь применим такую общую конструкцию. Пусть есть линейный код C, то есть подпространство в F_2^n. Возьмём его прообраз при отображении "приведения по модулю 2"
Z^n-> F_2^n.
Получится решётка — более того, подрешётка в Z^n. И теперь сожмём её в корень из 2 раз.
Z^n-> F_2^n.
Получится решётка — более того, подрешётка в Z^n. И теперь сожмём её в корень из 2 раз.
Victor Kleptsyn
19:29
Оказывается, что если мы начали унимодулярного кода — получится унимодулярная (т.е. с кообъёмом 1) решётка. Если с дважды чётного кода — чётная решётка.
Victor Kleptsyn
19:29
И из пополненного кода Хэмминга получается как раз решётка E_8, решётка Коркина-Золотарёва!
Victor Kleptsyn
19:36
Что, конечно, совершенно не очевидно.
Victor Kleptsyn
19:39
Кстати — если задана чётная решётка, то набор векторов длины \sqrt{2} в ней образует систему корней: конечное множество векторов, отражения относительно перпендикулярных им гиперплоскостей сохраняют это множество. (Это не полное определение — см. https://en.wikipedia.org/wiki/Root_system#Definition — но остальное в нашем случае будет выполнено совсем автоматически)
И это следует из формулы для отражения: отражение относительно перпендикулярной к v гиперплоскости это
И это следует из формулы для отражения: отражение относительно перпендикулярной к v гиперплоскости это
Victor Kleptsyn
19:41
И если <v,v>=2, то в правой части стоит просто
u-<u,v>*v.
Поскольку чётная решётка автоматически целая, то это тоже вектор из той же решётки — поэтому такое отражение сохраняет всю решётку, в частности, набор её кратчайших векторов.
u-<u,v>*v.
Поскольку чётная решётка автоматически целая, то это тоже вектор из той же решётки — поэтому такое отражение сохраняет всю решётку, в частности, набор её кратчайших векторов.
Victor Kleptsyn
19:49
Так вот, кратчайшие вектора решётки E_8 образуют систему корней E_8. И хорошее упражнение — посчитать, сколько их.
Victor Kleptsyn
19:49
In reply to this message
Можно посчитать для конструкции через чётную сумму и сдвиг на (1/2,...,1/2).
Victor Kleptsyn
19:52
Тогда будет:
(8*7/2) * 4 = 112 векторов вида (±1,±1, 0,...,0), где ±1 стоят на произвольных двух местах;
и ещё 128 векторов вида (±1/2,±1/2,....,±1/2), где число знаков "-" чётно.
Итого 112+128=240.
(8*7/2) * 4 = 112 векторов вида (±1,±1, 0,...,0), где ±1 стоят на произвольных двух местах;
и ещё 128 векторов вида (±1/2,±1/2,....,±1/2), где число знаков "-" чётно.
Итого 112+128=240.
Victor Kleptsyn
19:53
Можно в конструкции через код Хэмминга: в расширенном коде Хэмминга один вектор нулевой, один состоит из восьми единиц, а остальные 16-2=14 веса 4.
Victor Kleptsyn
19:55
Каждый из них порождает 16*14= 224 прообраза длины \srqt{2} (потому что все возможные выборы знака).
Да ещё (как и в случае с шахматной решёткой, их тоже надо не забыть!)
2*8=16 векторов вида (±\sqrt{2},0,...,0).
Итого: 224+16=240.
Да ещё (как и в случае с шахматной решёткой, их тоже надо не забыть!)
2*8=16 векторов вида (±\sqrt{2},0,...,0).
Итого: 224+16=240.
Victor Kleptsyn
20:01
Да — поскольку эти 240 векторов это кратчайшие вектора решётки, то контактное число в размерности 8 не меньше 240. Так вот, оно равно 240 — так что решётка E_8 в этом смысле оптимальна.
Victor Kleptsyn
20:02
А ещё можно посмотреть на производящую функцию для (половин) квадратов длин векторов решётки:
Victor Kleptsyn
20:03
Для решётки E_8 получаем
1 + 240 q + ... .
1 + 240 q + ... .
Victor Kleptsyn
20:06
А ещё можно посмотреть вот на такую функцию — ряд Эйзенштейна E_4 . Я не буду давать определение прямо сейчас, а ограничусь цитатой отсюда (https://en.wikipedia.org/wiki/Eisenstein_series#As_theta_functions ):
Victor Kleptsyn
20:07
Так вот, это — одно и то же число 240, и более того, эти ряды (ряд, пришедший из комплексного анализа, и ряд-производящая функция) совпадают!
Victor Kleptsyn
20:10
In reply to this message
Да, возвращаясь к системам корней, раз мы уже посчитали кратчайшие вектора — я процитирую одну страницу из той же брошюры Жени Смирнова про группы отражений и правильные многогранники, что я уже упоминал:
Victor Kleptsyn
20:16
И закончу свой сегодняшний рассказ тем, как решётка E_8 была построена в исходных работах Коркина и Золотарёва (а это ещё 1873 год!). Оказывается, они строили не решётку внутри пространства, а "пространство вокруг решётки". А именно — брали Z^8 и на нём задавали другое "скалярное произведение" (квадратичную форму). Тогда достаточно, чтобы оно было положительно определённым, чтобы квадраты элементов Z^8 были бы чётными, и чтобы определитель задающей его матрицы был бы равен 1.
Victor Kleptsyn
20:16
И, собственно, их статья так и называется — "О квадратичных формах":
Victor Kleptsyn
20:17
Ну и на этом я, пожалуй, на сегодня прекращаю дозволенные речи.
Victor Kleptsyn
15 June 2020
М
11:44
Математические байки
Давайте я продолжу рассказ про решётки. И нам тут понадобятся ещё две вещи, полезные и сами по себе.
Одна из них — это преобразование Фурье на прямой.
Одна из них — это преобразование Фурье на прямой.
Victor Kleptsyn
11:44
Возьмём сначала окружность длины L:
Victor Kleptsyn
11:45
В "хороших" (комплекснозначных) функциях на ней есть базис Фурье:
Victor Kleptsyn
11:45
Этот базис (записанный именно в таком виде) ортогональный, но не нормированный: скалярный квадрат каждого из векторов равен длине окружности L.
Victor Kleptsyn
11:46
Теперь можно любую "хорошую" функцию по такому базису разложить, пользуясь общей процедурой разложения по ортогональному базису — спроецируем её на каждый базисный вектор и сложим результаты:
Victor Kleptsyn
11:48
где y_k=k/L — соответствующие частоты.
Victor Kleptsyn
11:49
Но тогда на (1/L) можно посмотреть, как на разность двух соседних частот:
Victor Kleptsyn
11:49
И эта формула становится очень похожей на интегральную сумму Римана.
Victor Kleptsyn
11:53
Если теперь есть "хорошая" (достаточно гладкая и убывающая на бесконечности, например) функция f на прямой — её можно приблизить функциями f_{(L)} на окружностях L всё большей длины. Например, взяв сумму по L-сдвигам
\sum_n f(x+nL),
или ещё как-нибудь. Каждую такую функцию можно разложить в ряд Фурье:
\sum_n f(x+nL),
или ещё как-нибудь. Каждую такую функцию можно разложить в ряд Фурье:
Victor Kleptsyn
11:54
И в пределе при L, стремящемся к бесконечности, получается
Victor Kleptsyn
11:57
И вот у нас и появились прямое и обратное преобразования Фурье на прямой.
Victor Kleptsyn
11:59
На всякий случай — это рассуждение пока на уровне "рукомахания". Его можно чуть-чуть доработать напильником — но мне хотелось его показать в таком виде, чтобы было видно, "откуда 2π".
Victor Kleptsyn
12:01
Собственно, тут есть различные конвенции — можно писать преобразование Фурье без 2π в экспоненте — но тогда придётся либо делить на корень из 2π при каждом из переходов, либо в одну сторону не делить вообще, а в другую делить на 2π. И я помню, как я в своё время удивлялся, "откуда же оно взялось". Ну вот один способ это 2π понять — вот такой.
Да, и — на протяжении этого рассказа у нас 2π будет в экспоненте: для многих вещей тут так удобнее.
Да, и — на протяжении этого рассказа у нас 2π будет в экспоненте: для многих вещей тут так удобнее.
Victor Kleptsyn
12:04
Вторая обещанная общая вещь — это формула суммирования Пуассона.
Пусть опять на прямой задана достаточно хорошая (гладкая и хорошо убывающая) функция f. Оказывается, что сумма её значений в целых точках совпадает с суммой значений в целых точках её преобразования Фурье:
Пусть опять на прямой задана достаточно хорошая (гладкая и хорошо убывающая) функция f. Оказывается, что сумма её значений в целых точках совпадает с суммой значений в целых точках её преобразования Фурье:
Victor Kleptsyn
12:13
И удивительным образом, хоть утверждение симметричное по функции и её преобразованию Фурье — симметричного доказательства я не знаю.
Victor Kleptsyn
12:15
Давайте её докажем — и для этого давайте сдвинем f на все целые числа и просуммируем (собственно, мы такую "периодизацию" уже обсуждали чуть выше, только тогда сдвигали на кратные L):
Victor Kleptsyn
12:15
In reply to this message
Получилась функция F на единичной окружности. У которой левая часть формулы Пуассона — это просто значение в нуле.
Victor Kleptsyn
12:19
Но если аккуратно посмотреть — то коэффициенты Фурье функции F это в точности значения преобразования Фурье исходной f в целых точках:
Victor Kleptsyn
12:24
А сумма коэффициентов Фурье — это и есть значение F в нуле (потому что каждая из экспонент в нём даёт единицу). И вот всё и доказано:
Victor Kleptsyn
12:29
А что будет, если мы в левой части будем суммировать не по Z, а по L*Z? Тогда, как несложно видеть, появится множитель (1/L) в правой части, а сумма там будет не по Z, а по (1/L)*Z — по тем частотам, которые укладываются на фактор-окружность длины L:
Victor Kleptsyn
12:31
Наконец, а что будет, если взять функцию не на прямой, а в пространстве, и суммировать её по решётке? Тогда в правой части в знаменателе будет кообъём решётки, а сумма там будет по двойственной решётке тех частот, с которыми может "звучать" тор-фактор:
Victor Kleptsyn
12:34
In reply to this message
Как раз, если мы захотим устроить ряд Фурье на торе R^n/Λ, то условием, чтобы экспонента
\exp(2πi * <u,x>)
на нём была определена (то есть не менялась при сдвигах на Λ, и будет, что u принадлежит двойственной к Λ решётке).
\exp(2πi * <u,x>)
на нём была определена (то есть не менялась при сдвигах на Λ, и будет, что u принадлежит двойственной к Λ решётке).
Victor Kleptsyn
12:37
Вот. Ну и — формула Пуассона замечательная как сама по себе, так и своими применениями.
(По этой дороге я сейчас не пойду, но функциональное уравнение для дзета-функции Римана — которое связывает \zeta(s) с \zeta(1-s) — тоже вытаскивается отсюда, и это простая и короткая история.)
(По этой дороге я сейчас не пойду, но функциональное уравнение для дзета-функции Римана — которое связывает \zeta(s) с \zeta(1-s) — тоже вытаскивается отсюда, и это простая и короткая история.)
Victor Kleptsyn
12:42
Давайте теперь вернёмся к вопросу плотности упаковок — и попробуем посмотреть, а как, хотя бы в принципе, можно было бы их оценивать? Вот хоть как-нибудь — учитывая, что пространство всех упаковок бесконечно-мерное (по n координат на каждый центр); и даже если ограничиться только решётками — работать в 8*8=64-мерном пространстве всех решёток вряд ли вызовет энтузиазм в исследовании функции на экстремум обычными методами...
Victor Kleptsyn
12:44
Так вот — есть такая замечательная теорема. Её доказали одновременно Горбачёв и Кон и Элкис:
Victor Kleptsyn
12:44
И это — такая "машина" по производству верхних оценок на плотности.
Victor Kleptsyn
12:46
Нашли удачную функцию f — получили оценку. Нашли другую — получили оценку получше. Лишь бы условия на эту функцию выполнялись, а дальше — конвеер.
Victor Kleptsyn
12:48
И доказывается она удивительно несложно. Давайте для начала посмотрим на случай упаковок решётками: пусть есть какая-то упаковка Λ с минимальным расстоянием не меньше 1; мы хотим оценить её плотность.
Victor Kleptsyn
12:49
In reply to this message
Применим к f формулу суммирования Пуассона — просуммировав её по этой решётке. И кусочки паззла как раз и сложатся.
Victor Kleptsyn
12:51
В левой части стоит сумма f по решётке, где есть единственное положительное слагаемое, f(0). Потому что все остальные вектора решётки имеют длину не меньше 1 — а там f <= 0 по условию. Так что левая часть не больше f(0).
Victor Kleptsyn
12:52
В правой части стоит произведение как раз искомой плотности — 1/covol Λ — на сумму уже, наоборот, неотрицательных слагаемых. Поэтому эта сумма не меньше, чем просто слагаемое в 0.
Victor Kleptsyn
12:59
Вот паззл и сложился — вот так получается оценка на плотность любой решётки!
А удивительным образом, общий случай делается техникой очень похожей на решёточный. Достаточно взять большой-большой куб, в котором плотность будет близка к предельной, и повторить то, что мы видим внутри него, периодичным образом. Получается упаковка, которая есть объединение конечного числа сдвигов одной и той же решётки. И очень похожей техникой (просуммировать f по всем векторам разностей — как раз на этом воспользовавшись, что они все не короче 1) и получается дословно та же оценка.
А удивительным образом, общий случай делается техникой очень похожей на решёточный. Достаточно взять большой-большой куб, в котором плотность будет близка к предельной, и повторить то, что мы видим внутри него, периодичным образом. Получается упаковка, которая есть объединение конечного числа сдвигов одной и той же решётки. И очень похожей техникой (просуммировать f по всем векторам разностей — как раз на этом воспользовавшись, что они все не короче 1) и получается дословно та же оценка.
Victor Kleptsyn
13:11
Собственно, до доказательства оптимальности E_8 осталось совсем чуть-чуть.
Первый шаг простой: если есть пара из решётки Λ и функции f, для которых все неравенства в доказательстве обращаются в равенства — то верхняя оценка для Λ тоже обращается в равенство, и значит, Λ и есть наилучшая возможная упаковка (раз её плотность оценивает сверху любую другую).
Первый шаг простой: если есть пара из решётки Λ и функции f, для которых все неравенства в доказательстве обращаются в равенства — то верхняя оценка для Λ тоже обращается в равенство, и значит, Λ и есть наилучшая возможная упаковка (раз её плотность оценивает сверху любую другую).
Victor Kleptsyn
13:20
Так что если бы найти такую функцию f(r), которая не просто удовлетворяет условиям теоремы Горбачёва-Кона-Элкиса, а ещё и обращается в ноль на длинах её ненулевых векторов, а её преобразование Фурье (только как сферически-симметричной многомерной, а не как одномерной функции) — на длинах векторов двойственной решётки, то мы бы победили.
А E_8 — решётка очень хорошая. Мы знаем её квадраты длин векторов — это все чётные числа, а двойственная решётка с ней просто совпадает. Так, может быть, случится чудо и такая функция найдётся?
А E_8 — решётка очень хорошая. Мы знаем её квадраты длин векторов — это все чётные числа, а двойственная решётка с ней просто совпадает. Так, может быть, случится чудо и такая функция найдётся?
Victor Kleptsyn
13:23
Так вот — Марина Вязовска в своей работе 2016 года такую функцию явно предъявила! (Как преобразование Лапласа от некоторой модулярной формы )
Victor Kleptsyn
13:25
(см.: https://arxiv.org/abs/1603.04246 )
И это, мне кажется, замечательная ситуация — когда до содержания работы 2016 года можно дойти вот за такой вот рассказ...
И это, мне кажется, замечательная ситуация — когда до содержания работы 2016 года можно дойти вот за такой вот рассказ...
Victor Kleptsyn
13:29
Да, ещё забавная иллюстрация — можно такой техникой доказать, что Z это плотнейшая упаковка на прямой (правда, сложный результат?).
А именно — нам нужно, чтобы преобразование Фурье \hat{f} было бы везде неотрицательно, но занулялось во всех целых точках, кроме нуля.
Если нужно зануление — давайте возьмём sin(πx). Если неотрицательность — возведём в квадрат. Если кроме нуля — ну поделим на x (точнее, уже на x^2, а ещё лучше, на (πx)^2), ноль в нуле и исчезнет.
А именно — нам нужно, чтобы преобразование Фурье \hat{f} было бы везде неотрицательно, но занулялось во всех целых точках, кроме нуля.
Если нужно зануление — давайте возьмём sin(πx). Если неотрицательность — возведём в квадрат. Если кроме нуля — ну поделим на x (точнее, уже на x^2, а ещё лучше, на (πx)^2), ноль в нуле и исчезнет.
Victor Kleptsyn
13:31
А от чего это преобразование Фурье? (Раз у нас чётные функции — можно спросить вместо этого, кто у него преобразование Фурье?)
Victor Kleptsyn
13:32
Если бы был просто sin^2(πx), то это была бы линейная комбинация экспонент exp(-2πix), 1, exp(2πix); соответственно, преобразование Фурье давало бы дельта-функции в точках -1,0,1 (с правильными коэффициентами).
Деление на x^2 соответствует двукратному интегрированию; одно интегрирование превращает дельта-функцию в скачок, второе делает из него скачок производной.
Деление на x^2 соответствует двукратному интегрированию; одно интегрирование превращает дельта-функцию в скачок, второе делает из него скачок производной.
Victor Kleptsyn
13:33
Вот и получается, что исходная функция f должна быть вот такой:
Victor Kleptsyn
13:34
И она и впрямь удовлетворяет условиям — неположительна за радиусом 1 и обращается в ноль в целых точках (собственно, она при |x|>=1 вообще в тождественный ноль обратилась).
Victor Kleptsyn
13:34
Ура!
Victor Kleptsyn
13:34
Мы доказали, что Z — плотнейшая упаковка на прямой. :)
Victor Kleptsyn
19 June 2020
М
15:28
Математические байки
In reply to this message
Давайте немного продолжим про множества Жюлиа и Мандельброта. Вот мы в прошлый раз закончили на том, почему множество Мандельброта так определяют: потому что именно для таких параметров c (заполненное) множество Жюлиа отображения z^2+c будет связным — а не "канторовой пылью".
А чем вообще хорошо множество Жюлиа — и почему каждый раз я к нему добавляю слово "заполненное"?
А чем вообще хорошо множество Жюлиа — и почему каждый раз я к нему добавляю слово "заполненное"?
Victor Kleptsyn
15:29
Давайте опять посмотрим на самый простой пример, c=0, когда итерируемое отображение это просто возведение в квадрат, z->z^2.
Victor Kleptsyn
15:33
Что происходит при его итерациях? Точки с |z|>1 убегают на бесконечность, точки с |z|<1 падают в 0, а единичная окружность |z|=1 сохраняется — и на ней возведение в квадрат действует, удваивая аргумент
φ->2φ.
φ->2φ.
Victor Kleptsyn
15:36
А удвоение угла на единичной окружности — это самый классический пример хаотической динамики — при которой малейшая ошибка в определении начального положения через небольшое число итераций приводит к полной невозможности что-либо сказать о положении образа.
(Скажем, если мы знали начальную точку с точностью 10^{-9} — то какие-нибудь 30 итераций и всё, её образ уже может быть где угодно.)
(Скажем, если мы знали начальную точку с точностью 10^{-9} — то какие-нибудь 30 итераций и всё, её образ уже может быть где угодно.)
Victor Kleptsyn
15:38
Так вот — правильное определение (не-заполненного) множества Жюлиа, которое можно применять не только к полиномиальным, но и к рациональным отображениям, такое: это множество точек, где динамика хаотична.
Victor Kleptsyn
15:41
Если говорить более аккуратно: во-первых, давайте превратим комплексную плоскость в сферу Римана, добавив к ней бесконечность (можно представлять себе картинку стереографической проекции).
Victor Kleptsyn
15:41
(Картинка опять из Dimensions — на этот раз из главы про расслоение Хопфа)
Victor Kleptsyn
15:43
И говоря о том, близко точки или далеко, будем иметь в виду расстояние на сфере — то есть 1000 и 10000 не очень-очень далеко, а напротив, очень близко друг к другу — и к бесконечности.
Victor Kleptsyn
15:48
И скажем, что у точки z_0 орбита неустойчива по Ляпунову, если для некоторого ε>0 сколь угодно близко к z_0 есть точки, образы которых когда-нибудь удаляются (на сфере Римана) от образов z хотя бы на ε.
Ну и если это записать совсем формально, то получится
Ну и если это записать совсем формально, то получится
Victor Kleptsyn
15:48
Так вот — множество Жюлиа это множество точек, орбиты которых неустойчивы по Ляпунову.
Victor Kleptsyn
15:50
И в случае полиномиального отображения, как оказывается (но что неочевидно), это — как раз граница заполненного множества Жюлиа. И наоборот, заполненное множество Жюлиа это просто множество Жюлиа плюс всё, что оно ограничивает.
Victor Kleptsyn
15:52
То, что граница заполненного множества Жюлиа будет состоять только из точек с неустойчивой орбитой, понять легко — действительно, это точки, образы которых остаются ограниченными, но сколь угодно близко к которым (по определению границы — пересечение замыканий множества и дополнения) есть точки, на бесконечность убегающие. Вот и неустойчивость.
Victor Kleptsyn
15:53
Вот вложение в другую сторону неочевидно. На самом деле, верно даже более сильное утверждение: множество Жюлиа является границей области притяжения любой притягивающей орбиты:
Victor Kleptsyn
15:54
(Это — кусочек из замечательной книги Дж. Милнора, "Голоморфная динамика", которую я очень рекомендую).
Victor Kleptsyn
15:58
Так что, если срочно нужно привести пример трёх (четырёх, пяти, ...) открытых множеств на плоскости с совпадающей границей, то можно сделать так. Взять отображение, у которого сколько нужно притягивающих орбит — например, взяв полиномиальное отображение
z-> z- 0.000001 (z-1)(z-2)...(z-5)
(неподвижные точки z=1,3 и 5 будут притягивающими — производная в них будет чуть меньше 1),
или, скажем, применив метод Ньютона к нахождению корней многочлена нужной степени (правда, тут получится уже рациональное отображение).
И взяв бассейны притяжения этих притягивающих орбит — границей каждого из этих бассейнов притяжения будет (одно и то же!) множество Жюлиа.
z-> z- 0.000001 (z-1)(z-2)...(z-5)
(неподвижные точки z=1,3 и 5 будут притягивающими — производная в них будет чуть меньше 1),
или, скажем, применив метод Ньютона к нахождению корней многочлена нужной степени (правда, тут получится уже рациональное отображение).
И взяв бассейны притяжения этих притягивающих орбит — границей каждого из этих бассейнов притяжения будет (одно и то же!) множество Жюлиа.
Victor Kleptsyn
16:04
Правда, если привести такой пример на экзамене, то могут попросить доказать все предыдущие утверждения... Но красиво ведь!
(Да, на всякий случай — примеры проще есть, и они строятся совсем "руками")
(Да, на всякий случай — примеры проще есть, и они строятся совсем "руками")
Victor Kleptsyn
16:07
In reply to this message
Это — три бассейна притяжения для метода Ньютона, применённого к кубическому многочлену; картинку я взял из статьи Дирка Шляйхера "Complex Dynamics, the Mandelbrot Set, and Newton’s Method — or: On Useless and Useful Mathematics" из сборника "An Invitation to Mathematics".
Victor Kleptsyn
16:10
А вот (из его же статьи с R. Stoll-ом — https://arxiv.org/pdf/1508.02935.pdf ) — картинка для областей притяжения у корней многочлена 12-й степени:
Victor Kleptsyn
М
16:40
Математические байки
Кстати — комплексно-дифференцируемое отображение (по определению) "под большим увеличением" рядом с точкой похоже на свою линейную часть в этой точке (по крайней мере, когда производная не обращается в ноль). А умножение на комплексное число это поворотная гомотетия.
Victor Kleptsyn
16:40
а) (оффтопик, но раз уж подвернулась возможность) Именно это — что производная это умножение на комплексное число — и говорится в условиях Коши-Римана — что нужно добавить к вещественной дифференцируемости, чтобы получилась комплексная.
б) (почти не оффтопик) именно поэтому там, где производная не обращается в ноль, комплексно-дифференцируемые функции конформны: у маленькой-маленькой фигуры они могут изменить размер, но почти не искажают форму
б) (почти не оффтопик) именно поэтому там, где производная не обращается в ноль, комплексно-дифференцируемые функции конформны: у маленькой-маленькой фигуры они могут изменить размер, но почти не искажают форму
Victor Kleptsyn
16:44
Вот, кстати, иллюстрация из всё того же фильма Dimensions (https://youtu.be/bY4DS1RwwAE?t=306 ), где авторы взяли фотографию замечательного математика Адриана Дуади — и применили к ней рациональную функцию:
Victor Kleptsyn
16:46
Видно, что хоть глобально картинка и исказилась —рука и стала больше головы — у каждого маленького кусочка пропорции не поменялись (если закрыть всё, кроме руки, или всё, кроме головы, то они по отдельности выглядят вполне нормально — а не, скажем, вытянутыми в два раза в какую-нибудь сторону).
Victor Kleptsyn
16:47
Так вот — а то, к чему я всё это упоминал, это
в) а что будет происходить рядом с точкой множества Жюлиа?
в) а что будет происходить рядом с точкой множества Жюлиа?
Victor Kleptsyn
16:48
(Допустим, для полиномиального отображения, чтобы было проще).
Victor Kleptsyn
17:01
Да, пока я не забыл это проговорить — множество Жюлиа сохраняется отображением, причём как взятием образа, так и взятием полного прообраза. Потому что если у двух точек орбиты совпадают, начиная с какого-то места, то у них и устойчивость одинаковая.
(И я тут замёл под ковёр, что под действием комплексно-дифференцируемой непостоянной функции образ открытого множества открыт: в отличие от вещественной ситуации, когда у отображения x^2 образ рядом с нулём покрывает только половину окрестности, в комплексном случае первый ненулевой член a*z^n ряда Тейлора всё равно даст все возможные направления-аргументы и закроет окрестность, а следующие ему не помешают.)
(И я тут замёл под ковёр, что под действием комплексно-дифференцируемой непостоянной функции образ открытого множества открыт: в отличие от вещественной ситуации, когда у отображения x^2 образ рядом с нулём покрывает только половину окрестности, в комплексном случае первый ненулевой член a*z^n ряда Тейлора всё равно даст все возможные направления-аргументы и закроет окрестность, а следующие ему не помешают.)
Victor Kleptsyn
17:05
Множество Жюлиа замкнуто (что, вообще-то, надо доказывать, но мы в это поверим) — а его дополнение, которое называется множеством Фату, соответственно, открыто (и тоже инвариантно как под действием образа, так и при взятии полного прообраза).
Victor Kleptsyn
17:10
In reply to this message
Мы знаем, что у самой этой точки орбита остаётся ограниченной — но сколь угодно близко есть точки, убегающие далеко (для полиномиального отображения — на бесконечность). Если было бы можно вольно обращаться с пределами, то мы могли бы сказать, что производная стремится к бесконечности, и поэтому маленькие окрестности будут становиться всё больше и больше. И если к этому добавить инвариантность множества Жюлиа — то его часть, заключённая в такой (сколь угодно маленькой) окрестности, должна расползтись до чего-то макроскопического — и глядя на наш исходный пример с удвоением окружности, можно предположить, что до всего множества Жюлиа.
Про производную, на самом деле, неправда — критическая точка (где уже производная f, а тем самым и всех итераций f^n, обращается в ноль) может множеству Жюлиа принадлежать. А вот заключение про "расползание" правильное — и я опять процитирую книгу Милнора:
Про производную, на самом деле, неправда — критическая точка (где уже производная f, а тем самым и всех итераций f^n, обращается в ноль) может множеству Жюлиа принадлежать. А вот заключение про "расползание" правильное — и я опять процитирую книгу Милнора:
Victor Kleptsyn
17:14
И вот объяснение самоподобия множества Жюлиа — действительно его малые окрестности динамика растягивает на его всего, и можно надеяться, с не слишком сильным искажением формы (ибо конформность, хотя я опять жульничаю с порядком пределов).
Victor Kleptsyn
М
17:34
Математические байки
In reply to this message
Давайте теперь вернёмся к множеству Мандельброта и с того, с чего я вообще начинал этот рассказ — с анимации о поведении на границе главной кардиоиды. И для начала поймём, что вообще это за кардиоида такая.
Victor Kleptsyn
17:41
Вот, собственно, она изображена — на кадре из видео "Times Tables, Mandelbrot and the Heart of Mathematics" (https://youtu.be/qhbuKbxJsk8?t=273 ) :
Victor Kleptsyn
17:46
Так вот — как это ни смешно, мы пока что знаем только одну точку из множества Мандельброта, точку c=0 (просто потому, что про другие мы не задумывались). И там z=0 это суперпритягивающая точка: все близкие точки к ней стремятся, причём с суперэкспоненциальной скоростью (потому что расстояние до неё не делится, скажем, пополам или даже на 10, а возводится в квадрат). И, в частности, не убегает на бесконечность.
Victor Kleptsyn
17:47
А что будет, если мы возьмём какое-нибудь близкое c?
Victor Kleptsyn
17:50
Если мы возьмём маленькое по модулю, но ненулевое c, то z=0 уже не будет неподвижной точкой. Но где-то неподалёку будет неподвижная точка z_0, решение уравнения z_0=P(z_0)=z_0^2+c, производная в которой (по непрерывности) будет очень маленькой по модулю.
В частности, эта точка будет притягивающей: все достаточно близкие к ней будут стремится. Значит, заполненное множество Жюлиа будет включать в себя её маленькую окрестность.
В частности, эта точка будет притягивающей: все достаточно близкие к ней будут стремится. Значит, заполненное множество Жюлиа будет включать в себя её маленькую окрестность.
Victor Kleptsyn
17:53
И значит, точка c принадлежит множеству Мандельброта. Что можно увидеть двумя способами. С одной стороны, если поверить в то, что два определения множества Мандельброта (не-уход 0 на бесконечность и заполненное множество Жюлиа не канторово) эквивалентны, то вот мы нашли целую окрестность, которая не убегает на бесконечность.
Victor Kleptsyn
17:54
С другой — есть такое очень красивое утверждение: любая притягивающая периодическая орбита обязана притянуть к себе хотя бы одну критическую точку.
Victor Kleptsyn
18:02
Оно доказывается так: сначала оказывается, что динамику отображения P рядом с притягивающей неподвижной точкой z_0=P(z_0) можно линеаризовать: можно найти новые координаты y=h(z), в которых применение отображения превращается просто в умножение на его производную λ=P'(z_0). И, более того, такое линеаризующее отображение очень несложно ищется — пишется предел
Victor Kleptsyn
18:03
(давайте для простоты считать, что z_0=0, иначе сдвинем систему координат)
Victor Kleptsyn
18:04
и тогда из предела видно, что h(P(z))=λh(z), то есть h превращает применение P в умножение на λ.
Victor Kleptsyn
18:08
Но — пока притягивающая точка к себе не притянула хотя бы одну критическую, это соотношение позволяет "растягивать" область, где h^{-1} определено, всё дальше и дальше. И если и не притянет — то у нас будет конформная биекция между бассейном притяжения P до сопряжения и всей комплексной плоскостью (бассейном притяжения нуля) после. А это запрещено комплексным анализом (например, теоремой Лиувилля).
Victor Kleptsyn
18:11
Если вы за этим рассуждением не уследили, ничего страшного — можно запомнить только само утверждение, что притягивающая орбита всегда притягивает к себе хотя бы одну критическую точку.
Victor Kleptsyn
18:13
А в нашем случае P(z)=z^2+c критическая точка вообще лишь одна, это точка z=0. Значит, если есть притягивающая орбита — она притянет к себе орбиту z=0. В частности, образы z=0 не убегают на бесконечность — и это по определению и значит, что c из множества Мандельброта.
Victor Kleptsyn
18:14
In reply to this message
На самом деле, это утверждение (и следствия из него) вполне удивительны. Например, отсюда следует, что притягивающих орбит у P(z)=z^2+c может быть не больше одной — каков бы ни был их период!
Victor Kleptsyn
18:16
То есть, скажем, уравнение P^10(z)=z имеет кучу решений (как-никак, в левой части стоит многочлен степени 1024); кое-где мы посчитали по нескольку раз точки одной орбиты, но всё равно периодических орбит периода 10 много. А притягивающей может быть не больше одной из них!
Victor Kleptsyn
18:17
Мне очень нравится формулировка Ю. С. Ильяшенко — из его курса, на который я в студенческие годы ходил:
Каждая притягивающая орбита должна купить себе "трамвайный билетик" — критическую точку. Поэтому притягивающих орбит у рационального отображения не больше, чем критических точек.
Каждая притягивающая орбита должна купить себе "трамвайный билетик" — критическую точку. Поэтому притягивающих орбит у рационального отображения не больше, чем критических точек.
Victor Kleptsyn
18:19
Итак, в частности, пока у P(z)=z^2+c есть притягивающая неподвижная точка — параметр c из множества Мандельброта. А при каких c она есть?
Victor Kleptsyn
18:21
Можно к этому вопросу подойти двояко. Можно пойти "в лоб": написать квадратное уравнение на неподвижную точку, z=z^2+c, решить его, найдя неподвижную точку, найти в ней производную и попросить, чтобы она была меньше 1 по модулю.
Victor Kleptsyn
18:22
Но можно — и гораздо проще — пройти в обход, сыграв "от производной".
Victor Kleptsyn
18:25
А именно — мы же знаем, что производная λ=P'(z_0) в неподвижной точке z_0 должна быть меньше 1 по модулю — так давайте для каждой такой λ посмотрим, каким c она может соответствовать?
Victor Kleptsyn
18:25
Сначала найдём саму неподвижную точку: производная (z^2+c) это 2z, так что z_0=λ/2.
Victor Kleptsyn
18:26
А теперь из её неподвижности — и сам параметр c:
c=z_0-z_0^2 = λ/2 - λ^2/4.
c=z_0-z_0^2 = λ/2 - λ^2/4.
Victor Kleptsyn
18:32
Граница возможных c будет образом граничных λ — то есть единичной окружности. Если мы возьмём
λ=e^{i φ},
и будем смотреть, как с изменением угла φ меняется c, то мы увидим сумму двух слагаемых: одно, λ/2, это вектор длины 1/2, поворачивающийся с единичной скоростью, а второе, -λ^2/4, вдвое короче и поворачивается со вдвое большей скоростью.
λ=e^{i φ},
и будем смотреть, как с изменением угла φ меняется c, то мы увидим сумму двух слагаемых: одно, λ/2, это вектор длины 1/2, поворачивающийся с единичной скоростью, а второе, -λ^2/4, вдвое короче и поворачивается со вдвое большей скоростью.
Victor Kleptsyn
18:35
И тут уже несложно увидеть, что это кардиоида в её классическом определении — кривая, заметаемая точкой одной окружности при её качении по другой, такого же радиуса:
Victor Kleptsyn
18:36
In reply to this message
(кадр из того же видео "Times Tables, Mandelbrot and the Heart of Mathematics")
Victor Kleptsyn
18:37
Где окружности радиуса (1/4) — вектор из центра чёрной окружности в центр синей это λ/2, а вдвое быстрее поворачивающийся вектор из центра синей к отмеченной точке — это -λ^2/4.
Victor Kleptsyn
18:42
Вот отсюда в множестве Мандельброта и есть эта — "главная" — кардиоида. Но состоит оно далеко-далеко не только из неё. Скажем, если перейти из неё в соседнюю большую компоненту сверху, то там живёт "кролик Дуади", множество Жюлиа вот такого вида:
Victor Kleptsyn
18:46
In reply to this message
Явно видны два (немного разных) уха, тело и две лапы.
Victor Kleptsyn
18:47
А если перейти в другую компоненту — получится трёхлапый (и трёхухий) кролик-мутант:
Victor Kleptsyn
18:53
Можно взять точку z=i (дойдя до неё по одному из "усов" сверху):
Victor Kleptsyn
18:57
Можно, наоборот, уйти влево по оси абсцисс — и кстати, неожиданно увидеть там копию множества Мандельброта:
Victor Kleptsyn
18:58
Ну и вообще, если вы этого никогда не делали — я очень советую поиграть с такими картинками, увеличивая во много раз какую-нибудь часть множества Мандельброта и смотря на соответствующее множество Жюлиа. Там будет много красивого.
Victor Kleptsyn
19:12
Возвращаясь к кардиоиде — она же получается как огибающая "таблицы умножения на 2": если расставить много-много точек на равных расстояниях на окружности и соединить отрезком точку номер k с точкой номер 2k.
Victor Kleptsyn
19:13
In reply to this message
Тут мы взяли 21 точку — а вот что будет, если взять 200:
Victor Kleptsyn
19:16
И довольно несложно понять, почему это так: если мы соединяем точку z с точкой z^2 (а это и есть умножение на 2), то два таких очень близких отрезка пересекутся, разделившись в отношении 1:2 — таком же, как то, насколько смещаются z и z^2. И тогда точка такого пересечения будет
(1/3) z+ (2/3) z^2 = (1/3) (z+ z^2/2)
(1/3) z+ (2/3) z^2 = (1/3) (z+ z^2/2)
Victor Kleptsyn
19:16
И это и есть уже знакомый нам вид — а огибающая и есть кривая, которую заметают такие "точки пересечений при бесконечно малом смещении".
Victor Kleptsyn
19:20
Да — ещё кардиоида получается как каустика в конической "кофейной чашке", если одна из образующих конуса смотрит на Солнце:
Victor Kleptsyn
19:21
(фото Gérard Janot отсюда — https://commons.wikimedia.org/wiki/File:Caustique.jpg )
Victor Kleptsyn
19:25
Зато, если взять отражение от цилиндрического стакана, то получается половина нефроиды — кривой, которую можно увидеть либо через "таблицу умножения на 3", либо при внешнем качении по окружности другой, вдвое меньшей её:
Victor Kleptsyn
М
19:49
Математические байки
И проверить это совершенно несложно: собственно, вот соответствующая картинка —
Victor Kleptsyn
19:51
Видно, что если точка первого отражения параллельного пучка отстоит от точки его касания со стаканом на α, то придёт отражённый луч в точку 3α — а огибающая таких отражённых лучей и будет (видимой глазом) каустикой.
Victor Kleptsyn
19:53
Ну и на этом на сегодня я прекращаю дозволенные речи — а в следующий раз собираюсь всё-таки проговорить, что же именно мы при движении вдоль кардиоиды видим.
Victor Kleptsyn
4 July 2020
М
13:01
Математические байки
Давайте я немного поговорю о том, что происходит рядом с главной кардиоидой. И начну с точки (1/4): "уголка" кардиоиды, где у отображения
z-> z^2 + (1/4)
есть параболическая неподвижная точка z_0=(1/2), производная в которой равна 1 — по линейным членам нет ни притяжения, ни отталкивания.
Если увеличить рядом с ней множество Мандельброта, то мы увидим много-много его как-бы-копий; таких же, как мы видим во многих других местах. И это пока, вроде бы, совершенно непонятно (оно же множество параметров, почему его кусочки на него похожи?!) — но к этому мы перейдём чуть позже.
z-> z^2 + (1/4)
есть параболическая неподвижная точка z_0=(1/2), производная в которой равна 1 — по линейным членам нет ни притяжения, ни отталкивания.
Если увеличить рядом с ней множество Мандельброта, то мы увидим много-много его как-бы-копий; таких же, как мы видим во многих других местах. И это пока, вроде бы, совершенно непонятно (оно же множество параметров, почему его кусочки на него похожи?!) — но к этому мы перейдём чуть позже.
Victor Kleptsyn
13:01
Само множество Мандельброта —
Victor Kleptsyn
13:01
И увеличение рядом с c=1/4 :
Victor Kleptsyn
13:02
Так вот — давайте сначала посмотрим, что происходит ровно в точке (1/4). Если перенести неподвижную точку z_0=1/2 в начало координат, сделав замену w=z-z_0, то отображение примет вид
w-> w+w^2
(потому что должно получиться нечто квадратичное, без свободного члена, потому что 0 неподвижная точка, с линейным коэффициентом 1, потому что это производная в неподвижной точке, и со старшим коэффициентом 1, потому что так и было, а замена это параллельный перенос).
w-> w+w^2
(потому что должно получиться нечто квадратичное, без свободного члена, потому что 0 неподвижная точка, с линейным коэффициентом 1, потому что это производная в неподвижной точке, и со старшим коэффициентом 1, потому что так и было, а замена это параллельный перенос).
Victor Kleptsyn
13:03
А как устроены его итерации рядом с неподвижной точкой?
Когда w маленькое, смещение w^2 его сильно меньше — и можно вместо итераций отображения
w->w+w^2
думать о траектории w(t), заданном дифференциальным уравнением
w'=w^2.
А это уравнение очень хорошо решается — потому что
1=w'/w^2 = (-1/w)',
поэтому замена u=(-1/w) превращает его просто в u'=1.
Это постоянное поле скоростей на комплексной плоскости, где всё движется из бесконечности в бесконечность — а возвращаясь в координату w=-1/u, мы видим движение по окружностям:
Когда w маленькое, смещение w^2 его сильно меньше — и можно вместо итераций отображения
w->w+w^2
думать о траектории w(t), заданном дифференциальным уравнением
w'=w^2.
А это уравнение очень хорошо решается — потому что
1=w'/w^2 = (-1/w)',
поэтому замена u=(-1/w) превращает его просто в u'=1.
Это постоянное поле скоростей на комплексной плоскости, где всё движется из бесконечности в бесконечность — а возвращаясь в координату w=-1/u, мы видим движение по окружностям:
Victor Kleptsyn
13:04
Именно поэтому мы видим такой "клюв" рядом с неподвижной точкой z_0 у соответствующего множества Жюлиа:
Victor Kleptsyn
13:05
Точки справа от клюва убегают слишком далеко вправо от 0 — где дифференциальное уравнение уже не приближает отображение, и где |w| будет просто неограниченно нарастать (из-за возведения в квадрат).
Victor Kleptsyn
13:05
И кстати — похожесть множества Мандельброта и множества Жюлиа не случайна; по этой тропинке я сейчас не пойду — но покажу ещё пару картинок:
Victor Kleptsyn
13:05
Множество Жюлиа —
Victor Kleptsyn
13:06
И окрестность соответствующей ему точки множества Мандельброта:
Victor Kleptsyn
13:06
Другое множество Жюлиа —
Victor Kleptsyn
13:06
И окрестность соответствующего ему параметра c :
Victor Kleptsyn
13:06
Ещё одно множество Жюлиа —
Victor Kleptsyn
13:07
И окрестность соответствующего параметра в множестве Мандельброта:
Victor Kleptsyn
13:09
Давайте теперь вернёмся к нашему c=1/4 — и посмотрим, что происходит, когда мы двигаем c по вещественной прямой.
Victor Kleptsyn
13:10
Нам пока будет удобно использовать всё ту же координату w=z-1/2. В ней мы итерируем отображение
w->w+w^2+ε,
где ε=с-1/4.
w->w+w^2+ε,
где ε=с-1/4.
Victor Kleptsyn
13:11
Когда ε<0, у этого отображения две неподвижные точки, плюс и минус корень из (-ε); левая из них притягивающая, правая отталкивающая. При ε=0 они сливаются в одну параболическую, и при ε>0 уходят в комплексную область.
Victor Kleptsyn
13:20
Конечно, это означает, что при (вещественном) ε>0 мы не находимся в множестве Жюлиа — но это хороший момент, чтобы показать один важный эффект. Чем ближе ε к нулю, тем больше итераций нужно, чтобы "проскочить" от отрицательных w в положительные. Казалось бы, эффект такого может быть сколь угодно сильным. Но — давайте я покажу один слайд из доклада Mitsuhiro Shishikura,
https://www.math.univ-toulouse.fr/adrien2008/Slides/Shishikura.pdf :
https://www.math.univ-toulouse.fr/adrien2008/Slides/Shishikura.pdf :
Victor Kleptsyn
13:22
То есть — когда мы проходим слева направо, картинка "на выходе" (кривой верблюд справа) действительно получается искажённой. Но — искажение пропорций на ней равномерно ограничено — сколь бы малым ε ни был (хоть число итераций становится всё большим и большим).
Victor Kleptsyn
13:27
In reply to this message
Грубо говоря, причина в том, что хоть композиция получается и очень длинной — большую часть времени она применяется к очень маленькому верблюду. А чем меньше картинка — тем меньше добавляемое за один шаг искажение пропорций. Собственно, дифференцируемое отображение на то и дифференцируемое, чтобы под увеличением быть похожим на линейное — и потому почти не искажать пропорции на маленькой картинке; мы, кстати, это уже обсуждали на примере отображения, применяемого к фотографии Адриана Дуади.
Victor Kleptsyn
13:27
Так что суммарное искажение (если его аккуратно проконтролировать) остаётся равномерно ограниченным — и это частный случай очень часто применяемой (и очень мощной) техники контроля искажения .
Victor Kleptsyn
13:40
Если же мы поднимемся от положительных ε на кардиоиду — то одна из неподвижных точек, вместо того, чтобы отталкивать, начнёт просто "закручивать" (модуль производной в ней станет равен 1 — собственно, так главная кардиода и определяется) — а другая продолжит закручивать и отталкивать. И очень естественно, что множество Жюлиа тоже получится "с закручиванием":
Victor Kleptsyn
13:41
+увеличенная картинка вокруг нижней, отталкивающей+закручивающей, неподвижной точки:
Victor Kleptsyn
13:45
Давайте теперь перейдём к самой левой точке кардиоиды, c=-3/4, для которой неподвижной будет точка z_0=-1/2 с производной (-1). И, опять же, посмотрим, что там происходит.
Victor Kleptsyn
М
14:30
Математические байки
Как и раньше — посмотрим сначала, что происходит рядом с самой точкой z_0, работая в координате w=z-z_0.
Вообще — это хороший момент, чтобы сказать, что для квадратичных отображений есть разные естественные параметризации. Можно смотреть на отображение
z->z^2+c,
взяв за начало координат точку, где производная обращается в 0 (и попросив, чтобы z^2 было с коэффициентом 1).
Можно вместо этого сдвинуть начало координат в неподвижную точку; получится отображение
w->λw+w^2.
Правда, поскольку неподвижных точек две, одной точке c соответствуют два разных λ. Зато обратно пересчитывать очень просто — и мы это уже делали, когда находили кардиоиду: точка с производной λ в c-координате это z=λ/2, и чтобы она была неподвижной для z->z^2+c, нужно взять
c=λ/2 - (λ/2)^2.
Вообще — это хороший момент, чтобы сказать, что для квадратичных отображений есть разные естественные параметризации. Можно смотреть на отображение
z->z^2+c,
взяв за начало координат точку, где производная обращается в 0 (и попросив, чтобы z^2 было с коэффициентом 1).
Можно вместо этого сдвинуть начало координат в неподвижную точку; получится отображение
w->λw+w^2.
Правда, поскольку неподвижных точек две, одной точке c соответствуют два разных λ. Зато обратно пересчитывать очень просто — и мы это уже делали, когда находили кардиоиду: точка с производной λ в c-координате это z=λ/2, и чтобы она была неподвижной для z->z^2+c, нужно взять
c=λ/2 - (λ/2)^2.
Victor Kleptsyn
14:31
Наконец, можно сделать в координате w линейную замену — и вместо отображения
w->λw+w^2
получить отображение с любым другим коэффициентом при w.
w->λw+w^2
получить отображение с любым другим коэффициентом при w.
Victor Kleptsyn
14:32
Например, попросить, чтобы он равнялся (-λ) — или, что то же самое, принести в 1 второй прообраз неподвижной точки 0. И тогда получается логистическое отображение
w-> λw(1-w).
w-> λw(1-w).
Victor Kleptsyn
14:43
И есть картинка, которую всегда с логистическим отображением рисуют — где по оси абсцисс возможные значения λ, а по оси ординат — предельный режим, на который она выходит:
Victor Kleptsyn
14:48
Так вот — эта картинка обязана быть связанной с множеством Мандельброта, раз одно отображение из другого получается заменой координат. И действительно:
Victor Kleptsyn
14:49
(изображение отсюда — https://commons.wikimedia.org/wiki/File:Verhulst-Mandelbrot-Bifurcation.jpg )
Victor Kleptsyn
14:51
In reply to this message
Так вот, давайте поймём, что же происходит. Будем работать с отображением
w-> λw+w^2;
для него c=-3/4 соответствует λ=-1, то есть мы итерируем
w-> -w+w^2,
и хотим понять, что будет происходить рядом с его неподвижной точкой w=0.
w-> λw+w^2;
для него c=-3/4 соответствует λ=-1, то есть мы итерируем
w-> -w+w^2,
и хотим понять, что будет происходить рядом с его неподвижной точкой w=0.
Victor Kleptsyn
14:53
Для начала возведём это отображение в квадрат — применим его два раза:
Victor Kleptsyn
14:54
Если раскрыть скобки, то -(-w)=w, квадратичные члены сократятся, и останется
w-> w -2w^3 +w^4.
w-> w -2w^3 +w^4.
Victor Kleptsyn
М
15:43
Математические байки
То есть на вещественной прямой рядом с неподвижной точкой w=0 точки к ней приближаются — потому что w^3 того же знака, и вычитается.
Victor Kleptsyn
15:43
А как вообще ведут себя рядом с w=0 итерации отображения
w->w + a w^n + ... ?
(Наш случай — n=3 и a=-2)
w->w + a w^n + ... ?
(Наш случай — n=3 и a=-2)
Victor Kleptsyn
15:45
Как и раньше, приблизим итерации отображения
w->w+a w^n+...
траекториями движения вдоль векторного поля
w'=a w^n
(выкинув из векторного поля все старшие члены).
w->w+a w^n+...
траекториями движения вдоль векторного поля
w'=a w^n
(выкинув из векторного поля все старшие члены).
Victor Kleptsyn
15:50
In reply to this message
И если мы возьмём u=w^{-(n-1)}, то
u'=- (n-1) w'/w^n = -a (n-1).
То есть в u-координате у нас опять движение с постоянной скоростью из бесконечности в бесконечность, но когда мы вернёмся в координату w, нам придётся перейти к обратной величине 1/u (от чего образуются окружности, которые мы уже видели) и извлечь корень (n-1)-й степени (от чего вся картинка сожмётся по углу в (n-1) раз и (n-1) раз повторится).
u'=- (n-1) w'/w^n = -a (n-1).
То есть в u-координате у нас опять движение с постоянной скоростью из бесконечности в бесконечность, но когда мы вернёмся в координату w, нам придётся перейти к обратной величине 1/u (от чего образуются окружности, которые мы уже видели) и извлечь корень (n-1)-й степени (от чего вся картинка сожмётся по углу в (n-1) раз и (n-1) раз повторится).
Victor Kleptsyn
15:50
И мы увидим то, что называется цветок Ло-Фату; я приведу картинку из "Голоморфной динамики" Милнора, которую я тут уже упоминал:
Victor Kleptsyn
15:53
In reply to this message
Тут как притягивающих, так и отталкивающих лепестков n-1=3 — то есть это картина для n=4, например, для отображения
z->z - z^4
(я выбрал знак минус, чтобы правый лепесток, содержащий вещественные положительные числа, действительно получился притягивающим, а не отталкивающим).
z->z - z^4
(я выбрал знак минус, чтобы правый лепесток, содержащий вещественные положительные числа, действительно получился притягивающим, а не отталкивающим).
Victor Kleptsyn
15:58
И действительно, если нарисовать множество Жюлиа для c=-3/4 (то есть для λ=-1), то мы увидим убегающие вверх и вниз от неподвижной точки z_0=-1/2 "клювики", попадающие в зазор между притягивающими лепестками. Там точки убегут под действием итераций слишком далеко (за ту область, где векторное поле, у которого возвращаются все траектории, хорошо приближает итерации) — и уже не вернутся.
Victor Kleptsyn
15:59
Так что же происходит, когда параметр c пересекает (-3/4), или, что то же самое, когда λ переходит через (-1)?
Victor Kleptsyn
М
16:16
Математические байки
При λ=-1 к точке w=0 на вещественной прямой близкие к ней точки приближаются (пусть и очень медленно, потому что (-2w^3) много меньше w). При этом они прыгают, каждый раз меняя знак:
Victor Kleptsyn
16:18
Когда |λ| станет больше единицы, сама точка w=0 превратится в отталкивающую — близкие к ней точки от неё удаляются (ибо их модуль умножается примерно на |λ|>1) :
Victor Kleptsyn
16:21
Значит, где-то между далёкими точками (которые приближались — и всё ещё приближаются просто по непрерывности — скажем, w=-0.1 не почувствует эффекта при λ=-1.00000001) и близкими, которые уже начали удаляться, должен найтись общий для них предельных режим — притягивающая периодическая орбита периода 2:
Victor Kleptsyn
16:22
In reply to this message
(Слово "значит" тут нужно взять в кавычки — чтобы это стало строгим рассуждением, нужно действовать гораздо аккуратнее — но, надеюсь, "на уровне картинок" это достаточно убедительно.)
Victor Kleptsyn
16:26
Так вот — то, что мы увидели, называется бифуркацией удвоения периода: при переходе мультипликатора ("производной в") неподвижной точки через (-1) она теряет устойчивость — и из неё рождается периодическая орбита вдвое большего периода.
Victor Kleptsyn
16:28
Вот линии, которые этому соответствуют на диаграмме предельных режимов логистического отображения: сначала мы видим притягивающую неподвижную точку —
Victor Kleptsyn
16:29
А когда её мультипликатор пересекает (-1) — притягивающую орбиту периода 2:
Victor Kleptsyn
16:32
(Чтобы не запутаться: для логистического отображения
x->λx(1-x)
параметр λ это производная в 0 (коэффициент воспроизводства, когда кроликов/рыбок/... мало, и они друг другу не мешают) — а (-1) пересекает мультипликатор в другой неподвижной точке,
x_0=1-1/λ. )
x->λx(1-x)
параметр λ это производная в 0 (коэффициент воспроизводства, когда кроликов/рыбок/... мало, и они друг другу не мешают) — а (-1) пересекает мультипликатор в другой неподвижной точке,
x_0=1-1/λ. )
Victor Kleptsyn
16:34
Так вот — на самом деле, мы только что поняли, что происходит, когда λ для отображения
w-> λw+w^2
пересекает значение (-1) — или, что то же самое, параметр c для
z->z^2+c
пересекает c=-3/4. А именно — рождается новая притягивающая периодическая орбита!
w-> λw+w^2
пересекает значение (-1) — или, что то же самое, параметр c для
z->z^2+c
пересекает c=-3/4. А именно — рождается новая притягивающая периодическая орбита!
Victor Kleptsyn
16:38
In reply to this message
Но мы уже знаем, что это гарантирует попадание с в множество Мандельброта (или потому, что образы 0 будут этой орбитой притянуты, или потому, что заполненное множество Жюлиа содержит бассейн притяжения — и тем самым гарантировано не канторово).
Victor Kleptsyn
16:44
И вот та область параметров c, где есть притягивающая периодическая орбита периода 2 — это касающаяся главной кардиоиды в точке с=-3/4 гиперболическая компонента множества Мандельброта.
(На всякий случай, это не связная компонента — множество Мандельброта связно!)
(На всякий случай, это не связная компонента — множество Мандельброта связно!)
Victor Kleptsyn
16:45
Вот она —
Victor Kleptsyn
М
17:31
Математические байки
Да — давайте, прежде, чем идти дальше в комплексной динамике, я скажу пару слов из теории динамических систем/бифуркаций.
Во-первых, аналогичный сценарий бывает с дифференциальными уравнениями, и там называется бифуркацией Андронова-Хопфа:
Во-первых, аналогичный сценарий бывает с дифференциальными уравнениями, и там называется бифуркацией Андронова-Хопфа:
Victor Kleptsyn
17:31
- жила-была неподвижная точка — притягивающий фокус:
Victor Kleptsyn
17:33
- шло время, параметры системы менялись, и в некоторый момент пара комплексно-сопряжённых собственных значений пересекла мнимую ось:
Victor Kleptsyn
17:34
Далёкие точки всё ещё к неподвижной точке притягивались. Но близкие после этого пересечения начали от неё убегать:
Victor Kleptsyn
17:34
"Значит", родился притягивающий предельный цикл:
Victor Kleptsyn
17:36
И, собственно, если мы проведём через неподвижную точку прямую (например, горизонтальную) и посмотрим на отображение Пуанкаре (отображение первого возвращения), то мы увидим, что это совсем одна и та же картина: у отображения первого возвращения как раз мультипликатор переходит через (-1).
Victor Kleptsyn
М
17:52
Математические байки
Во-вторых, такой сценарий — потеря устойчивости при переходе пары сопряжённых собственных значений через мнимую ось — появляется в физике как флаттер.
Кстати, про флаттер — вот этот ролик minutephysics про разрушение Такомского моста ( https://youtu.be/6ai2QFxStxo?t=61 ) мне очень нравится; и — если вы не видели само его падение, я тоже очень советую посмотреть (вот тут одноминутный ролик — https://youtu.be/XggxeuFDaDU?t=19 — и вид огромной конструкции, ходящей ходуном, внушает).
Кстати, про флаттер — вот этот ролик minutephysics про разрушение Такомского моста ( https://youtu.be/6ai2QFxStxo?t=61 ) мне очень нравится; и — если вы не видели само его падение, я тоже очень советую посмотреть (вот тут одноминутный ролик — https://youtu.be/XggxeuFDaDU?t=19 — и вид огромной конструкции, ходящей ходуном, внушает).
Victor Kleptsyn
17:57
В-третьих: сценарий, который мы видели, это на самом деле только один из двух вариантов, мягкая потеря устойчивости (для Андронова-Хопфа — суперкритическая бифуркация). Мы посмотрели на квадрат нашего отображения в момент бифуркации, когда мультипликатор пересекал (-1), и коэффициент при w^3 был отрицательным. И в этом сценарии мы из просто неподвижной точки перешли в режим "малых биений" — притягивающей стала (близкая) периодическая орбита периода 2 (или предельный цикл для дифференциального уравнения).
Victor Kleptsyn
17:59
Но коэффициент мог получиться и положительным (скажем, возьмём отображение w->-w+w^2-10w^3). И тогда мы видим, что в момент бифуркации точка уже глобально неустойчива — все близкие точки от неё будут "далеко" убегать.
Victor Kleptsyn
18:03
Этот случай можно превратить в исходный, если перейти к обратному отображению (или обратить время для дифференциального уравнения). И сценарий тут получается таким:
Victor Kleptsyn
18:05
- до бифуркации есть притягивающая неподвижная точка;
- её бассейн притяжения (область устойчивости) ограничен (отталкивающей) периодической орбитой периода 2 (или отталкивающим предельным циклом для дифференциального уравнения)
- эта область всё уменьшается и уменьшается, и в момент бифуркации схлопывается в нашу неподвижную точку — которая уже в этот момент становится неустойчивой (но медленно), а сразу за бифуркационным значением параметра — неустойчивой и по линейным членам.
- её бассейн притяжения (область устойчивости) ограничен (отталкивающей) периодической орбитой периода 2 (или отталкивающим предельным циклом для дифференциального уравнения)
- эта область всё уменьшается и уменьшается, и в момент бифуркации схлопывается в нашу неподвижную точку — которая уже в этот момент становится неустойчивой (но медленно), а сразу за бифуркационным значением параметра — неустойчивой и по линейным членам.
Victor Kleptsyn
18:06
И это называется жёсткой потерей устойчивости, или субкритической бифуркацией Андронова-Хопфа.
Victor Kleptsyn
18:06
Вот тут — http://www.scholarpedia.org/article/Andronov-Hopf_bifurcation — есть очень хорошие картинки этих двух сценариев:
Victor Kleptsyn
18:07
http://www.scholarpedia.org/w/images/7/7f/SuperHopf.gif — мягкая потеря устойчивости (после бифуркации выход на устойчивый предельный цикл);
Victor Kleptsyn
18:08
http://www.scholarpedia.org/w/images/2/2d/SubHopf.gif — жёсткая потеря устойчивости (после бифуркации всё из окрестности неподвижной точки вылетает).
Victor Kleptsyn
18:15
И жёсткая потеря устойчивости — не такой очевидный сценарий, если об этом не задумываться (и очень неприятный, если система это что-то, что нужно контролировать, и её собственное время гораздо быстрее, чем то, с какой скоростью можно управлением подкручивать параметры).
Victor Kleptsyn
18:17
In reply to this message
Давайте теперь вернёмся к множеству Мандельброта (и, на самом деле, к логистическому отображению) — и продолжим двигаться влево по вещественной оси для c.
Victor Kleptsyn
18:21
В момент, когда мы только-только перешли в нашу новую гиперболическую компоненту, мультипликатор (производная за период) новой периодической орбиты периода 2 был положительным (и почти равнялся (-1)^2=1) ). Когда мы дойдём до c=-1, он обратится в ноль: периодической орбитой будет
0 -> -1 -> (-1)^2-1=0,
а производная в нуле нулевая. Кстати, в этот момент мы увидим множество Жюлиа — базилику :
0 -> -1 -> (-1)^2-1=0,
а производная в нуле нулевая. Кстати, в этот момент мы увидим множество Жюлиа — базилику :
Victor Kleptsyn
18:22
И когда мы уйдём левее c=-1 — мультипликатор станет отрицательным. Пока маленьким, но — все ведь понимают, что дальше произойдёт?
Victor Kleptsyn
18:34
При дальнейшем уменьшении c мультипликатор увеличивается по модулю, и при c=-5/4 становится равным (-1). После чего происходит ещё одна бифуркация удвоения периода — и притягивающей орбитой становится орбита порядка 4:
Victor Kleptsyn
18:37
Кстати, хорошее упражнение — проверить, что гиперболическая компонента множества Мандельброта, отвечающая притягивающим орбитам периода 2, не просто "круглая" — а круг и есть, с центром в точке c=-1 и радиусом (1/4), а мультипликатор орбиты периода 2 как раз и равен 4(c+1).
Victor Kleptsyn
18:39
Возвращаясь к бифуркациям — естественно, что на второй бифуркации всё не заканчивается, если двигать параметр c дальше влево, то в какой-то момент потеряет устойчивость и орбита периода 4, и родившаяся из неё орбита периода 8, и так далее. И происходит это "всё быстрее и быстрее", ускоряясь, как геометрическая прогрессия. Вот вид на гиперболическую компоненту с периодом 2 —
Victor Kleptsyn
18:40
Вот — увеличенный на компоненту с периодом 4:
Victor Kleptsyn
18:47
Вот тут в центре уже гиперболическая компонента с периодом 8 —
Victor Kleptsyn
18:49
И видно, что компоненты (например, их горизонтальные диаметры) убывают (асимтотически) как геометрическая прогрессия — со знаменателем 1/4.669...
Victor Kleptsyn
18:51
И можно спросить — а почему так происходит?
Victor Kleptsyn
18:52
И ещё — а что будет, если мы (забыв временно про комплексные числа) будем смотреть на такие же моменты бифуркаций для какого-нибудь другого семейства? Например, для семейства отображений
x -> μ sin(πx)
отрезка [0,1] в себя?
x -> μ sin(πx)
отрезка [0,1] в себя?
Victor Kleptsyn
18:54
Как и для логистического семейства
x -> λx(1-x),
при маленьких значениях μ всё сваливается в x=0. При μ>1/π ноль становится неустойчивой точкой — и появляется неподвижная точка внутри отрезка.
x -> λx(1-x),
при маленьких значениях μ всё сваливается в x=0. При μ>1/π ноль становится неустойчивой точкой — и появляется неподвижная точка внутри отрезка.
Victor Kleptsyn
18:56
При дальнейшем увеличении μ в некоторый момент μ_1 эта точка теряет устойчивость — и из неё рождается притягивающая орбита периода 2.
Увеличиваем μ дальше — при некотором значении μ_2 эта орбита тоже теряет устойчивость (мультипликатор переходит через (-1)), и рождается притягивающая орбита периода 4. И так далее...
Увеличиваем μ дальше — при некотором значении μ_2 эта орбита тоже теряет устойчивость (мультипликатор переходит через (-1)), и рождается притягивающая орбита периода 4. И так далее...
Victor Kleptsyn
18:57
Смотрим на то, с какой скоростью происходит "учащение" — то есть на предел
Victor Kleptsyn
18:57
И получаем... опять 4.669... !
Victor Kleptsyn
19:00
Естественно, что такое совпадение совершенно не случайно; это — универсальность Фейгенбаума—Кулле—Трессера.
А откуда она берётся — и что ещё происходит на главной кардиоиде и рядом с ней — я расскажу в следующий раз.
А откуда она берётся — и что ещё происходит на главной кардиоиде и рядом с ней — я расскажу в следующий раз.
Victor Kleptsyn
19:10
In reply to this message
P.S. Оказывается, про Такомский мост писали в "Квантике":
http://old.kvantik.com/art/files/pdf/2015-04.6-8.pdf
http://old.kvantik.com/art/files/pdf/2015-04.6-8.pdf
Victor Kleptsyn
19:22
А вот упомянутая там замедленная съёмка биений бумажки — https://www.youtube.com/watch?v=Y9-W9BaAyww (via https://kvantik.com/issue/2015/ )
Victor Kleptsyn
6 July 2020
М
14:27
Математические байки
Н
Непрерывное математическое образование 05.07.2020 21:54:54
https://youtu.be/wTJI_WuZSwE
новое видео от 3blue1brow
обсуждается примерно такая задача
«Тюремщик пообещал двум друзьям, что завтра первого из них приведут в комнату, где на каждой клетке шахматной доски лежит монета — либо вверх орлом, либо вверх решкой (но как именно, заранее неизвестно) — и предложат перевернуть одну из монет. После этого тюремщик перевернет одну из монет, приведет второго друга и предложит ему определить, какую из монет перевернул тюремщик. Если он определил правильно — обоих друзей отпустят. Как им освободиться?»
новое видео от 3blue1brow
обсуждается примерно такая задача
«Тюремщик пообещал двум друзьям, что завтра первого из них приведут в комнату, где на каждой клетке шахматной доски лежит монета — либо вверх орлом, либо вверх решкой (но как именно, заранее неизвестно) — и предложат перевернуть одну из монет. После этого тюремщик перевернет одну из монет, приведет второго друга и предложит ему определить, какую из монет перевернул тюремщик. Если он определил правильно — обоих друзей отпустят. Как им освободиться?»
Victor Kleptsyn
14:27
Н
Непрерывное математическое образование 06.07.2020 00:14:29
С.Грибок. Мудрецы, колпаки и арифметика конечных полей (Квант-2019-04)
в отличие от видео 3b1b, в этой статье никаких монет на шахматной доске нет… казалось бы
в отличие от видео 3b1b, в этой статье никаких монет на шахматной доске нет… казалось бы
Victor Kleptsyn
14:27
Н
Непрерывное математическое образование 06.07.2020 14:25:31
https://youtu.be/laAtv310pyk
видимо что-то такое в воздухе сейчас — Numberphile сегодня тоже про мудрецов в колпаках
видимо что-то такое в воздухе сейчас — Numberphile сегодня тоже про мудрецов в колпаках
Victor Kleptsyn
8 July 2020
М
12:15
Математические байки
Давайте я договорю про периодические компоненты рядом с главной кардиоидой. Вот мы посмотрели на то, что происходит, когда мы пересекаем её в точке с мультипликатором (-1) — рождается притягивающая периодическая орбита периода 2, а в момент пересечения квадрат отображения имеет вид
z -> z + Az^3 + ...;
у этой параболической точки два притягивающих (и два отталкивающих) лепестка Фату (собственно, f в каждой паре лепестки переставляет — на то у него и мультипликатор (-1)).
z -> z + Az^3 + ...;
у этой параболической точки два притягивающих (и два отталкивающих) лепестка Фату (собственно, f в каждой паре лепестки переставляет — на то у него и мультипликатор (-1)).
Victor Kleptsyn
12:16
А что происходит, если мультипликатор будет не (-1), а корнем кубическим из 1, если мы будем итерировать отображение
f : w-> λw + w^2,
где λ=exp(2πi/3) ?
Или, как мы уже научились пересчитывать,
z->z^2+c,
где с=(λ/2)-(λ/2)^2 ?
f : w-> λw + w^2,
где λ=exp(2πi/3) ?
Или, как мы уже научились пересчитывать,
z->z^2+c,
где с=(λ/2)-(λ/2)^2 ?
Victor Kleptsyn
12:18
Посмотрим теперь на отображение w->f^3(w). Ноль всё ещё неподвижная точка, и производная в нём (она же коэффициент при w) равна λ^3=1.
Если раскрыть скобки, то можно увидеть, что члены с w^2 и даже с w^3 сократятся. Это можно увидеть прямым вычислением — но правильнее всего заметить, что f и f^3 коммутируют, и w^4 — первая степень, ненулевой коэффициент при которой этому не противоречит. Поэтому
f^3(w) = w + A w^4 + ...,
и мы получаем параболическую точку с тремя притягивающими лепестками — которые f^3 сохраняет, а f переставляет по циклу.
Если раскрыть скобки, то можно увидеть, что члены с w^2 и даже с w^3 сократятся. Это можно увидеть прямым вычислением — но правильнее всего заметить, что f и f^3 коммутируют, и w^4 — первая степень, ненулевой коэффициент при которой этому не противоречит. Поэтому
f^3(w) = w + A w^4 + ...,
и мы получаем параболическую точку с тремя притягивающими лепестками — которые f^3 сохраняет, а f переставляет по циклу.
Victor Kleptsyn
12:21
Иными словами — "толстую" версию кролика Дуади:
Victor Kleptsyn
12:22
In reply to this message
А после пересечения главной кардиоиды мы попадаем в гиперболическую компоненту, где притягивающая орбита имеет период 3; её "центр" — параметр, при котором критическая точка 0 оказывается периодичной — и соответствует тому самому кролику, которого мы видели раньше.
Victor Kleptsyn
12:23
То же самое происходит, если мы посмотрим на отображение
f : w-> λw + w^2,
где λ=exp(2πi p/q) — корень q-й степени из единицы. Если посмотреть на
f^q(w)=w+ A w^m+...,
то первой выжившей степенью будет m=q+1-я — по тем же причинам, что f и f^q должны коммутировать:
f : w-> λw + w^2,
где λ=exp(2πi p/q) — корень q-й степени из единицы. Если посмотреть на
f^q(w)=w+ A w^m+...,
то первой выжившей степенью будет m=q+1-я — по тем же причинам, что f и f^q должны коммутировать:
Victor Kleptsyn
12:24
и раз одно равно другому, то λ^m=λ, то есть m=kq+1.
(Я не проверил, что собственно q+1-я степень действительно выживает — заметём это под ковёр.)
(Я не проверил, что собственно q+1-я степень действительно выживает — заметём это под ковёр.)
Victor Kleptsyn
12:28
Да — давайте я покажу тут пару картинок из записок мини-курса Arnaud Cheritat,
http://num.math.uni-goettingen.de/~summer/cheritat.pdf .
Во-первых, просто картинка лепестков — показывающая, как устроена динамика f^q рядом с параболической точкой:
http://num.math.uni-goettingen.de/~summer/cheritat.pdf .
Во-первых, просто картинка лепестков — показывающая, как устроена динамика f^q рядом с параболической точкой:
Victor Kleptsyn
12:29
И во-вторых, кусочек, на котором лепестки расширяются до перекрытия —
Victor Kleptsyn
12:31
In reply to this message
Верхняя картинка тут как раз напоминает "толстого кролика".
Victor Kleptsyn
12:32
In reply to this message
Итак, для λ=exp(2πi p/q) получаются q переставляющихся динамикой притягивающихся лепестков — а пересекая кардиоиду, мы попадаем в соответствующую гиперболическую компоненту. В частности, трёхухого кролика-мутанта мы видим, пересекая кардиоиду в точке с λ=i : четыре лепестка соответствуют телу и трём ушам.
Иными словами, это та компонента, куда мы переходим через
c=i/2-(i/2)^2=1/4+i/2.
(Сама эта точка соответствует "толстому" кролику, а обычно берут "центр" соответствующей компоненты — где точка 0 оказывается периодической.)
Иными словами, это та компонента, куда мы переходим через
c=i/2-(i/2)^2=1/4+i/2.
(Сама эта точка соответствует "толстому" кролику, а обычно берут "центр" соответствующей компоненты — где точка 0 оказывается периодической.)
Victor Kleptsyn
12:33
Вот тут я специально ввёл точные координаты вручную (а не ткнул мышкой) —
Victor Kleptsyn
12:35
Вот (взятая из Википедии) картинка гиперболических компонент — на которой подписаны соответствующие периоды:
https://commons.wikimedia.org/wiki/File:Mandelbrot_Set_–_Periodicities_coloured.png
https://commons.wikimedia.org/wiki/File:Mandelbrot_Set_–_Periodicities_coloured.png
Victor Kleptsyn
12:37
Итак, что происходит на главной кардиоиде в точке, соответствующей λ=exp(2πi p/q), мы разобрались.
А что будет, если взять λ, не являющееся корнем из 1:
λ=exp(2πi r), где r — иррациональное число?
А что будет, если взять λ, не являющееся корнем из 1:
λ=exp(2πi r), где r — иррациональное число?
Victor Kleptsyn
12:38
Оказывается, что если r "плохо приближается рациональными числами", то итерации f "усредняются" и приводят к тому, что точки не сближаются и не удаляются.
Victor Kleptsyn
12:38
Более точно — если r иррациональное, то можно написать "ряд замены"
h(w)=w+c_2 w^2+ c_3 w^3+...,
такой, что
h(f(w))=λ h(w) —
иными словами, такой, что в координате z=h(w) отображение f становится просто умножением на λ.
h(w)=w+c_2 w^2+ c_3 w^3+...,
такой, что
h(f(w))=λ h(w) —
иными словами, такой, что в координате z=h(w) отображение f становится просто умножением на λ.
Victor Kleptsyn
12:39
И пишется такой ряд просто по индукции — причём на очередном шаге, убирая коэффициент при w^{m+1}, приходится делить на (λ^m-1).
Victor Kleptsyn
12:42
Так что если r плохо приближается рациональными числами — то есть если степени λ^m не слишком близко (ну, насколько возможно) попадают к 1 — то есть надежда, что такой формальный ряд действительно сойдётся.
Что правда — только за этим довольно много всего стоит, включая дорогу, ведущую к КАМ-теории — теории Колмогорова-Арнольда-Мозера.
(А также слова "малые знаменатели", про которые теперь понятно, на что они намекают; для каких-то степеней всё-таки придётся делить на что-то маленькое, потому что все степени λ^m далеко от 1 быть не могут.)
Что правда — только за этим довольно много всего стоит, включая дорогу, ведущую к КАМ-теории — теории Колмогорова-Арнольда-Мозера.
(А также слова "малые знаменатели", про которые теперь понятно, на что они намекают; для каких-то степеней всё-таки придётся делить на что-то маленькое, потому что все степени λ^m далеко от 1 быть не могут.)
Victor Kleptsyn
12:43
Кстати —
В. И. Арнольд, "Малые знаменатели и проблемы устойчивости движения в классической и небесной механике", УМН, 1963, http://mi.mathnet.ru/umn6441
В. И. Арнольд, "Малые знаменатели и проблемы устойчивости движения в классической и небесной механике", УМН, 1963, http://mi.mathnet.ru/umn6441
Victor Kleptsyn
12:45
Туда мы сейчас не пойдём — зато я покажу один пример из астрономии, щели Кирквуда.
Сейчас известно довольно много астероидов — счёт идёт на сотни тысяч. Если построить гистограмму, "сколько нам известно астероидов с данным периодом обращения вокруг Солнца" — то получается вот что:
Сейчас известно довольно много астероидов — счёт идёт на сотни тысяч. Если построить гистограмму, "сколько нам известно астероидов с данным периодом обращения вокруг Солнца" — то получается вот что:
Victor Kleptsyn
12:46
(Картинка из Википедии — https://upload.wikimedia.org/wikipedia/commons/archive/d/d3/20161213014817%21Kirkwood_Gaps.svg )
Victor Kleptsyn
12:51
То есть — на периодах, которые "хорошо соизмеримы" с периодом обращения Юпитера, мы астероидов почти не видим. В некоторых (весьма сильных) кавычках можно сказать, что на "хорошо иррациональных" орбитах влияние Юпитера усредняется. А вот на рациональных он на каждом обороте "подтягивает" астероид (точнее, параметры его орбиты) в одну и ту же сторону (а Юпитер, как-никак, аж 1/1000 от массы Солнца, так что эффект от него за миллионы лет весьма заметный) — и в итоге таких астероидов не остаётся.
(Давайте я сразу скажу, что соизмеримость периодов именно гарантированной проблемы не создаёт. Есть, к примеру, резонанс 1:2:4 между периодами обращения лун Юпитера — Ганимедом, Европой и Ио; см. https://en.wikipedia.org/wiki/Orbital_resonance . Но это, насколько я понимаю, скорее редкость.)
(Давайте я сразу скажу, что соизмеримость периодов именно гарантированной проблемы не создаёт. Есть, к примеру, резонанс 1:2:4 между периодами обращения лун Юпитера — Ганимедом, Европой и Ио; см. https://en.wikipedia.org/wiki/Orbital_resonance . Но это, насколько я понимаю, скорее редкость.)
Victor Kleptsyn
12:52
Но вернёмся к нашей комплексной динамике.
Мы выяснили, что если коэффициент r для динамики с λ=exp(2πi r) рациональный, r=p/q — то точка параболическая, и за ней начинается другая компонента.
Если иррациональный и рациональными плохо приближающийся — то рядом с такой точкой динамика приводится к виду "умножение на λ" (то есть точки не сближаются и не удаляются). Это то, что называется диском Зигеля, и вот пример такого множества Жюлиа — для r, равного золотому сечению:
Мы выяснили, что если коэффициент r для динамики с λ=exp(2πi r) рациональный, r=p/q — то точка параболическая, и за ней начинается другая компонента.
Если иррациональный и рациональными плохо приближающийся — то рядом с такой точкой динамика приводится к виду "умножение на λ" (то есть точки не сближаются и не удаляются). Это то, что называется диском Зигеля, и вот пример такого множества Жюлиа — для r, равного золотому сечению:
Victor Kleptsyn
12:56
А вот его же изображение из той же Википедии —
https://commons.wikimedia.org/wiki/File:Quadratic_Golden_Mean_Siegel_Disc_IIM.png
https://commons.wikimedia.org/wiki/File:Quadratic_Golden_Mean_Siegel_Disc_IIM.png
Victor Kleptsyn
М
13:17
Математические байки
Ну хорошо, если λ=exp(2πi r), и r рациональное, то мы ответ более-менее знаем. Если r иррациональное и рациональными числами плохо приближается — тоже. А если хорошо? Если, к примеру, r это классический пример трансцендентного числа — сумма ряда
\sum_n 1/10^{n!} ?
Если коротко, то "всё интересно" (и тут есть слова "точка Кремера" ).
\sum_n 1/10^{n!} ?
Если коротко, то "всё интересно" (и тут есть слова "точка Кремера" ).
Victor Kleptsyn
13:20
In reply to this message
И по тропинкам, которые начинаются с этого вопроса — который почти автоматически возникает при взгляде на ту анимацию, с которой я весь этот рассказ начал — мы сейчас попробуем пройти.
Victor Kleptsyn
13:23
Долгое время был открытым такой вопрос: может ли множество Жюлиа у полиномиального отображения иметь положительную меру?
Этот вопрос был бы тривиальным, если бы его задавали про заполненное множество Жюлиа — про те точки, которые не убегают на бесконечность. Например, для z^2 это (замкнутый) единичный диск.
Но — его спрашивали про настоящее множество Жюлиа, то, на котором динамика хаотична — иными словами, про границу заполненного множества Жюлиа.
Скажем, для z->z^2 это просто единичная окружность — конечно, имеющая меру ноль (то есть "занимающая нулевую площадь").
Этот вопрос был бы тривиальным, если бы его задавали про заполненное множество Жюлиа — про те точки, которые не убегают на бесконечность. Например, для z^2 это (замкнутый) единичный диск.
Но — его спрашивали про настоящее множество Жюлиа, то, на котором динамика хаотична — иными словами, про границу заполненного множества Жюлиа.
Скажем, для z->z^2 это просто единичная окружность — конечно, имеющая меру ноль (то есть "занимающая нулевую площадь").
Victor Kleptsyn
13:26
Так вот — всего, что мы сейчас увидели, достаточно, чтобы (в общих чертах) посмотреть, как Xavier Buff и Arnaud Cheritat построили (см. https://arxiv.org/pdf/math/0605514.pdf ) пример — причём как раз на главной кардиоиде:
Victor Kleptsyn
13:32
In reply to this message
И идея, собственно, очень простая и красивая. Давайте начнём с r (которое у них α), которое бы плохо приближалось рациональными. Например, с α, которое было бы золотым сечением. Тогда заполненное множество Жюлиа содержит диск Зигеля — который мы уже видели — и потому имеет положительную меру. А неподвижная точка сидит "в центре" этого диска — вокруг неё "всё крутится".
Victor Kleptsyn
13:42
In reply to this message
Теперь давайте обрубим цепную дробь α где-то глубоко-глубоко, получив вместо α близкое к нему рациональное число с огромным знаменателем q. Тогда мы получим параболическую точку, от которой будут убегать q узких "клювов неустойчивости" (таких же, как зазор между ушами и телом у "толстого кролика")
Victor Kleptsyn
13:51
А что будет, если вместо того, чтобы обрубать совсем, мы заменим какой-нибудь большой по номеру элемент цепной дроби на огромное число — но цепная дробь после него останется?
С одной стороны, если это число и впрямь совсем-совсем огромное — то новое α' настолько близко к соответствующему p/q (как если бы мы в этом месте цепную дробь обрубили), что "клювы" неустойчивости (которые не принадлежат заполненному множеству Жюлиа) почти останутся — так что заполненное множество Жюлиа будет ими "прорезано". С другой — за счёт "хвоста" новое число α' всё ещё (асимптотически) плохо приближается рациональными — так что мы всё ещё увидим диск Зигеля, просто его граница начала заходить внутрь диска для исходного α.
И вот картинка из их статьи —
С одной стороны, если это число и впрямь совсем-совсем огромное — то новое α' настолько близко к соответствующему p/q (как если бы мы в этом месте цепную дробь обрубили), что "клювы" неустойчивости (которые не принадлежат заполненному множеству Жюлиа) почти останутся — так что заполненное множество Жюлиа будет ими "прорезано". С другой — за счёт "хвоста" новое число α' всё ещё (асимптотически) плохо приближается рациональными — так что мы всё ещё увидим диск Зигеля, просто его граница начала заходить внутрь диска для исходного α.
И вот картинка из их статьи —
Victor Kleptsyn
М
15:15
Математические байки
Остаётся повторить такую процедуру счётное число раз — и обеспечить, чтобы заполненное множество Жюлиа для такой последовательности α_n становилось бы всё более "изрезанным" — но чтобы на каждом шаге на эти разрезы терялась всё меньшая и меньшая часть площади. Тогда в пределе заполненное множество Жюлиа совпадёт со своей границей — с настоящим множеством Жюлиа — а мера у него всё ещё будет положительной. И ура!
Victor Kleptsyn
15:18
Так что где-то в том "мелькании разрезов", которые мы видели на исходной анимации — появляются и построенные — в 2006 году, совсем не так давно — такой процедурой множества Жюлиа положительной меры.
(Ну и я, конечно, замёл какое-то число деталей под ковёр...)
(Ну и я, конечно, замёл какое-то число деталей под ковёр...)
Victor Kleptsyn
15:18
Кстати, такой трюк — счётное число последовательных поправок, чтобы что-нибудь обеспечить в пределе — применяется довольно часто (собственно, на классическую канторову диагональ можно смотреть как на пример его применения).
Victor Kleptsyn
15:24
Давайте посмотрим на пару точных картинок рядом с α-золотым сечением.
Вот тут, каюсь, я сжульничал и для большей похожести на картинку статьи перепрыгнул в одну из соседних компонент (как раз в точке, отвечающей рациональному приближению к золотому сечению):
Вот тут, каюсь, я сжульничал и для большей похожести на картинку статьи перепрыгнул в одну из соседних компонент (как раз в точке, отвечающей рациональному приближению к золотому сечению):
Victor Kleptsyn
15:24
А вот тут уже всё честно — заменили золотое сечение на некоторое близкое α':
Victor Kleptsyn
15:28
In reply to this message
Это не совсем то возмущение, что в статье — я тут сильно меньше увеличиваю меняемый элемент цепной дроби, чем надо; может быть, поэтому мы видим этакие "завитушки" — зато получается как раз похоже на то "закручивающееся мелькание", которое мы в анимации Мэтта Хэндерсона иногда видим.
Victor Kleptsyn
15:29
Давайте попробуем одну из этих "завитушек" увеличить —
Victor Kleptsyn
М
16:39
Математические байки
Видно, что спираль резко обрывается — вот её ещё увеличенная версия:
Victor Kleptsyn
16:41
Она обрывается настолько резко, что я даже подумал, не зря ли я тут на программу наговариваю — может быть, это я чего-то не понимаю?
Victor Kleptsyn
М
17:11
Математические байки
Но нет — всё правильно: есть 13 переставляющихся по циклу спиралей; здесь 13 это число Фибоначчи — знаменатель приближения α как 8/13 — это то самое место, где я почти-оборвал цепную дробь золотого сечения 1/(1+1/(1+1/(1+1/(...)))).
Victor Kleptsyn
17:19
Внутри этих спиралей есть отталкивающая периодическая орбита периода 13 — с чуть большим 1 по модулю мультипликатором (производной за период):
| 0.9998485 - 0.0618222 i | = 1.001758
И, соответственно, спирали должны на неё наматываться (потому что множество Жюлиа инвариантно).
| 0.9998485 - 0.0618222 i | = 1.001758
И, соответственно, спирали должны на неё наматываться (потому что множество Жюлиа инвариантно).
Victor Kleptsyn
17:21
Для контроля — вот картинка, которую тут строит программа XaoS (спасибо Михаилу Раскину за наводку):
Victor Kleptsyn
17:22
In reply to this message
То есть — вот здесь, например, программа действительно делает недостаточно итераций, и под этим увеличением рисует заметно-неправильное множество.
Victor Kleptsyn
17:23
И возникает вопрос: хорошо, а как определить, сколько ждать надо?
Victor Kleptsyn
17:25
В этом месте должна бы начинать звучать драматическая музыка — потому что на слова "определить, сколько времени нужно ждать" одной из первых ассоциаций является алгоритмически неразрешимая проблема останова.
Victor Kleptsyn
17:31
А именно — если мы рассматриваем компьютер (с бесконечной памятью; машину Тьюринга, чтобы формализовать слово "компьютер"), на котором будем запускать программы — то нет никакого универсального алгоритмического способа по любой программе правильно сказать, закончит ли она когда-нибудь работу, или нет.
Victor Kleptsyn
17:32
То есть — есть очевидные случаи (скажем, если первой же командой идёт "закончить работу", или первым же делом программа сваливается в бесконечный цикл).
Victor Kleptsyn
17:35
Есть менее очевидные, которые всё ещё можно обработать. Но нет никакого алгоритма, позволяющего правильно дать ответ во всех случаях.
Victor Kleptsyn
17:38
Потому что — пусть такой алгоритм ( = программа) существует:
Victor Kleptsyn
17:40
Испортим эту программу (которая должна была бы давать ответ всегда): пусть она зависает вместо того, чтобы печатать "OK" — но аккуратно печатает "FAIL":
Victor Kleptsyn
17:40
А теперь запустим его самого на себе:
Victor Kleptsyn
17:42
И получим классический парадокс лжеца: если он останавливается, то он должен был бы зависнуть из-за того, как мы его испортили (вместо того, чтобы напечатать "OK"), а если он зависает, то должен был бы добросовестно напечатать "FAIL" и остановиться.
Victor Kleptsyn
17:42
(спасибо Анне Горденко за рисунки :) )
Victor Kleptsyn
17:44
На самом деле — я тут чуть-чуть сжульничал: чтобы рассуждения выше стали совсем правдой, нужно сказать, что мы рассматриваем пару из программы и входных данных — а эти рассуждения доказывают алгоритмическую неразрешимость проблемы самоприменимости: "остановится ли программа, если её запустить на её собственном коде в качестве входных данных?"
Victor Kleptsyn
17:47
Но если бы мы могли решать, остановится ли данная программа на данных начальных данных — то и про частный случай, "запустить на своём собственном коде", смогли бы ответить. А мы только что увидели, что даже для этого частного случая никакого алгоритма нет.
Victor Kleptsyn
17:48
И это — теорема Алана Тьюринга 1936 года.
Victor Kleptsyn
18:02
Так вот — есть метод, который позволяет иногда ответить на вопрос, останавливается ли программа: скажем, подождать годик, вдруг остановится. И кстати — это не такой дурацкий способ!
Я приведу цитату из (очень живым языком написанной) статьи А. Разборова в сборнике "Студенческих чтений НМУ", https://www.mccme.ru/free-books/globus/iumlectures1.pdf , которую (как и весь сборник — и последовавшие за ним выпуски "Глобуса") очень советую:
Я приведу цитату из (очень живым языком написанной) статьи А. Разборова в сборнике "Студенческих чтений НМУ", https://www.mccme.ru/free-books/globus/iumlectures1.pdf , которую (как и весь сборник — и последовавшие за ним выпуски "Глобуса") очень советую:
Victor Kleptsyn
18:03
Но проблема этого метода — всегда остаётся сомнение, а достаточно ли мы подождали?
Victor Kleptsyn
18:05
Так вот — теперь, и при взгляде на множество Жюлиа и его построение ("подождать достаточно долго"), должно закрасться то же подозрение. Так вот — закрадывается оно по делу — и я тут процитирую статью Бравермана и Ямпольского (https://arxiv.org/pdf/math/0610340.pdf ) :
Victor Kleptsyn
18:08
То есть — заполненное множество Жюлиа построить можно (что уже неочевидно). Но вот для настоящего множества Жюлиа — для границы заполненного — это уже неправда!
Есть такие c, которые можно "указать явно" (точнее, написать программу, задающую их со сколь угодно высокой точностью) — что никакой алгоритм не сможет сколь угодно точно это множество нарисовать.
Есть такие c, которые можно "указать явно" (точнее, написать программу, задающую их со сколь угодно высокой точностью) — что никакой алгоритм не сможет сколь угодно точно это множество нарисовать.
Victor Kleptsyn
М
18:49
Математические байки
Про ренормализацию и константу Фейгенбаума я расскажу в следующий раз; а пока порекламирую видео Veritasium
https://www.youtube.com/watch?v=ovJcsL7vyrk —
и Numberphile
https://www.youtube.com/watch?v=FFftmWSzgmk +
https://www.youtube.com/watch?v=NGMRB4O922I +
https://www.youtube.com/watch?v=4LQvjSf6SSw
И на этом на сегодня я завершаю дозволенные речи.
https://www.youtube.com/watch?v=ovJcsL7vyrk —
и Numberphile
https://www.youtube.com/watch?v=FFftmWSzgmk +
https://www.youtube.com/watch?v=NGMRB4O922I +
https://www.youtube.com/watch?v=4LQvjSf6SSw
И на этом на сегодня я завершаю дозволенные речи.
Victor Kleptsyn
9 July 2020
М
17:56
Математические байки
Н
Непрерывное математическое образование 09.07.2020 09:19:34
поздравляем Сергея Константиновича Ландо с 65-летием!
завтра (10.07) — конференция, https://math.hse.ru/announcements/376454323.html
завтра (10.07) — конференция, https://math.hse.ru/announcements/376454323.html
Victor Kleptsyn
10 July 2020
М
12:47
Математические байки
Н
Непрерывное математическое образование 10.07.2020 10:57:33
https://mccme.ru/free-books/lando/lando-genfunc.pdf
напомним также про небольшую книгу С.К.Ландо про производящие функции
«Предметом нашего исследования будут задачи перечислительной комбинаторики. Они заключаются в подсчете числа объектов, принадлежащих некоторому семейству конечных множеств. (…)
Как правило, задача перечислительной комбинаторики «в принципе» разрешима: для каждого множества из семейства можно выписать все его элементы и таким образом узнать их число. Проблема, однако, состоит в том, чтобы найти «хорошее» решение, не требующее выписывания всех элементов изучаемых множеств.
Определить, что такое хорошее решение, довольно трудно. Зачастую можно лишь сравнить два решения и сказать, какое из них лучше.
При решении задач перечислительной комбинаторики очень полезно рассматривать производящие многочлены (или, более общо, производящие ряды). (…) Операции с комбинаторными объектами очень естественно выражаются в терминах производящих функций. (…)
Привлечение методов из смежных областей математики (например, из анализа) дает новый взгляд на перечислительные задачи и позволяет находить неожиданные подходы к их решению.»
«Мне хотелось написать простую и доступную книгу, уделив внимание в первую очередь ярким примерам, а не общим теориям (которые, к тому же, зачастую отсутствуют). (…) Предлагаемая вниманию читателей книга написана на основе специального курса, читавшегося студентам Независимого московского университета в 1992–99 гг.»
«Лекции о производящих функциях» легли в основу и более подробной книги «Введение в дискретную математику», https://biblio.mccme.ru/node/2720/ (соответствующей уже курсам на матфаке ВШЭ)
напомним также про небольшую книгу С.К.Ландо про производящие функции
«Предметом нашего исследования будут задачи перечислительной комбинаторики. Они заключаются в подсчете числа объектов, принадлежащих некоторому семейству конечных множеств. (…)
Как правило, задача перечислительной комбинаторики «в принципе» разрешима: для каждого множества из семейства можно выписать все его элементы и таким образом узнать их число. Проблема, однако, состоит в том, чтобы найти «хорошее» решение, не требующее выписывания всех элементов изучаемых множеств.
Определить, что такое хорошее решение, довольно трудно. Зачастую можно лишь сравнить два решения и сказать, какое из них лучше.
При решении задач перечислительной комбинаторики очень полезно рассматривать производящие многочлены (или, более общо, производящие ряды). (…) Операции с комбинаторными объектами очень естественно выражаются в терминах производящих функций. (…)
Привлечение методов из смежных областей математики (например, из анализа) дает новый взгляд на перечислительные задачи и позволяет находить неожиданные подходы к их решению.»
«Мне хотелось написать простую и доступную книгу, уделив внимание в первую очередь ярким примерам, а не общим теориям (которые, к тому же, зачастую отсутствуют). (…) Предлагаемая вниманию читателей книга написана на основе специального курса, читавшегося студентам Независимого московского университета в 1992–99 гг.»
«Лекции о производящих функциях» легли в основу и более подробной книги «Введение в дискретную математику», https://biblio.mccme.ru/node/2720/ (соответствующей уже курсам на матфаке ВШЭ)
Victor Kleptsyn
М
13:45
Математические байки
И — я в дополнение ещё порекламирую книгу Ландо-Звонкина "Графы на поверхностях":
https://www.rfbr.ru/rffi/ru/books/o_26646
https://www.rfbr.ru/rffi/ru/books/o_26646
Victor Kleptsyn
М
16:09
Математические байки
In reply to this message
Слайд из идущего сейчас доклада Д. Звонкина:
Victor Kleptsyn
11 July 2020
М
19:27
Математические байки
Немного оффтопик, но может быть, не все ещё видели, что на небе сейчас есть яркая комета — Neowise.
Я вот в своё время не посмотрел на комету Хейла-Боппа (https://ru.wikipedia.org/wiki/C/1995_O1_(%D0%A5%D0%B5%D0%B9%D0%BB%D0%B0_%E2%80%94_%D0%91%D0%BE%D0%BF%D0%BF%D0%B0) ) — не знаю, почему, но узнал о том, что она была, только много лет спустя, а тогда "прощёлкал клювом".
Я вот в своё время не посмотрел на комету Хейла-Боппа (https://ru.wikipedia.org/wiki/C/1995_O1_(%D0%A5%D0%B5%D0%B9%D0%BB%D0%B0_%E2%80%94_%D0%91%D0%BE%D0%BF%D0%BF%D0%B0) ) — не знаю, почему, но узнал о том, что она была, только много лет спустя, а тогда "прощёлкал клювом".
Victor Kleptsyn
М
19:27
Математические байки
A
AstroBlog 11.07.2020 13:10:32
Сейчас на небе можно увидеть комету невооруженным глазом. Лично я до сих пор еще не видела кометы без бинокля или телескопа. Красивое и редкое событие!
Комету Neowise сейчас особенно здорово наблюдать тем, кто живет южнее 60 широты. В Питере пока слишком светло и я, например, не смогла увидеть комету прошлой ночью, наблюдая за облаками.
Коротко: комету лучше наблюдать около полуночи, ниже и левее, чем звезда Капелла. В ближайшие дни можно продлить прямую Капелла – Менкалинан (Бета Возничего) и отложить за Менкалинан такой же отрезок.
Мне понравились обновляемые ежедневно поисковые карты на этом ресурсе: https://theskylive.com/c2020f3-info
Кроме того, здесь же опубликованы полезные ссылки на информацию о комете. Правда, все на английском.
Прикрепляю картинку для поиска отсюда: https://skyandtelescope.org/astronomy-news/anticipation-grows-for-comets-neowise-and-lemmon/
На русском есть отличный FAQ от AstroAlert: https://vk.com/astro.nomy?w=wall-727032_224245
Комету Neowise сейчас особенно здорово наблюдать тем, кто живет южнее 60 широты. В Питере пока слишком светло и я, например, не смогла увидеть комету прошлой ночью, наблюдая за облаками.
Коротко: комету лучше наблюдать около полуночи, ниже и левее, чем звезда Капелла. В ближайшие дни можно продлить прямую Капелла – Менкалинан (Бета Возничего) и отложить за Менкалинан такой же отрезок.
Мне понравились обновляемые ежедневно поисковые карты на этом ресурсе: https://theskylive.com/c2020f3-info
Кроме того, здесь же опубликованы полезные ссылки на информацию о комете. Правда, все на английском.
Прикрепляю картинку для поиска отсюда: https://skyandtelescope.org/astronomy-news/anticipation-grows-for-comets-neowise-and-lemmon/
На русском есть отличный FAQ от AstroAlert: https://vk.com/astro.nomy?w=wall-727032_224245
Victor Kleptsyn
М
19:40
Математические байки
(Присоединяюсь: FAQ от AstroAlert действительно отличный)
Ну и завершая кометную тему — некоторое время назад я прочитал (удивительно недавно — как-то в школьно-университетские годы я астрономией не очень интересовался; shame on me) про комету Шумейкеров-Леви — столкнувшуюся с Юпитером. И вот количество выделившейся при этом энергии — внушает:
Ну и завершая кометную тему — некоторое время назад я прочитал (удивительно недавно — как-то в школьно-университетские годы я астрономией не очень интересовался; shame on me) про комету Шумейкеров-Леви — столкнувшуюся с Юпитером. И вот количество выделившейся при этом энергии — внушает:
Victor Kleptsyn
19:41
Это — цитата из Википедии (https://ru.wikipedia.org/wiki/D/1993_F2_(%D0%A8%D1%83%D0%BC%D0%B5%D0%B9%D0%BA%D0%B5%D1%80%D0%BE%D0%B2_%E2%80%94_%D0%9B%D0%B5%D0%B2%D0%B8) ) — а вот сюда идёт сноска к аналогичному абзацу из англоВики:
http://www.physics.sfasu.edu/astro/sl9/cometfaq2.html#Q3.1
http://www.physics.sfasu.edu/astro/sl9/cometfaq2.html#Q3.1
Victor Kleptsyn
М
19:57
Математические байки
6 миллионов мегатонн это, мм, впечатляет.
Victor Kleptsyn
12 July 2020
М
18:04
Математические байки
Н
Непрерывное математическое образование 12.07.2020 18:03:38
https://mccme.ru/dubna/lect2020/
С 2001 года каждое лето во второй половине июля проходит Летняя школа «Современная математика» для старшеклассников и младшекурсников.
В этом году ЛШСМ не будет. Но примерно в те же сроки и для той же аудитории будет несколько математических вечеров: часовая лекция + вопросы-обсуждение после нее. Приятный бонус онлайн-режима — в отличие от лекций ЛШСМ, сюда есть возможность пригласить всех желающих.
Г.Ю.Панина, В.А.Клепцын, А.Ю.Окуньков, É.Ghys, А.А.Логунов, С.О.Горчинский, А.П.Веселов и В.Ю.Овсиенко — с 20 по 32 июля, примерно через день, на совсем разные темы (подробности постепенно появляются по ссылке).
С 2001 года каждое лето во второй половине июля проходит Летняя школа «Современная математика» для старшеклассников и младшекурсников.
В этом году ЛШСМ не будет. Но примерно в те же сроки и для той же аудитории будет несколько математических вечеров: часовая лекция + вопросы-обсуждение после нее. Приятный бонус онлайн-режима — в отличие от лекций ЛШСМ, сюда есть возможность пригласить всех желающих.
Г.Ю.Панина, В.А.Клепцын, А.Ю.Окуньков, É.Ghys, А.А.Логунов, С.О.Горчинский, А.П.Веселов и В.Ю.Овсиенко — с 20 по 32 июля, примерно через день, на совсем разные темы (подробности постепенно появляются по ссылке).
Victor Kleptsyn
13 July 2020
М
22:41
Математические байки
Г
Геометрия-канал 13.07.2020 22:27:02
Divide et impera
Принцип «разделяй и властвуй» хорошо работает не только в большой политике, но и математике и информатике. Мы посмотрим на геометрические задачи о «делении поровну», обслуживающие этот принцип, как классические, так и современные. В рассказе появятся важные математические понятия: класс Эйлера, кривая Веронезе, конфигурационное пространство (что-то явно, что-то неявно).
Для разминки перед лекцией рекомендуется подумать над следующими задачами:
1) всякая плоская фигура может быть разделена двумя прямолинейными разрезами на четыре равные по площади части;
2) не всякая плоская фигура может быть разделена тремя прямолинейными разрезами на семь равных по площади частей.
Лекция: 20 июля (пн), 16:00 (обсуждение в 17:30)
Лектор: Гаянэ Юрьевна Панина (ПОМИ РАН)
Что это вообще?
А это летняя школа «Современная математика» в этом году проходить не будет, зато все желающие могут попасть на прекрасные математические вечера ЛШСМ.
Подробности и анонсы других вечеров: https://www.mccme.ru/dubna/lect2020/
Но это не всё.
Там пишут, что уровень высок, поэтому заранее советуют посмотреть видеозаписи прошлых школ. Вот они, все под рукой, там много интересного: https://mccme.ru/dubna/courses/
#лекции #видео
Принцип «разделяй и властвуй» хорошо работает не только в большой политике, но и математике и информатике. Мы посмотрим на геометрические задачи о «делении поровну», обслуживающие этот принцип, как классические, так и современные. В рассказе появятся важные математические понятия: класс Эйлера, кривая Веронезе, конфигурационное пространство (что-то явно, что-то неявно).
Для разминки перед лекцией рекомендуется подумать над следующими задачами:
1) всякая плоская фигура может быть разделена двумя прямолинейными разрезами на четыре равные по площади части;
2) не всякая плоская фигура может быть разделена тремя прямолинейными разрезами на семь равных по площади частей.
Лекция: 20 июля (пн), 16:00 (обсуждение в 17:30)
Лектор: Гаянэ Юрьевна Панина (ПОМИ РАН)
Что это вообще?
А это летняя школа «Современная математика» в этом году проходить не будет, зато все желающие могут попасть на прекрасные математические вечера ЛШСМ.
Подробности и анонсы других вечеров: https://www.mccme.ru/dubna/lect2020/
Но это не всё.
Там пишут, что уровень высок, поэтому заранее советуют посмотреть видеозаписи прошлых школ. Вот они, все под рукой, там много интересного: https://mccme.ru/dubna/courses/
#лекции #видео
Victor Kleptsyn
15 July 2020
М
18:51
Математические байки
In reply to this message
Вдогонку к спиралям и комплексным числам — есть вот такое четырёхсекундное видео
https://images.math.cnrs.fr/media/51/video.mp4
(отсюда — https://images.math.cnrs.fr/L-effet-Droste.html ; правда, там по-французски, но можно только посмотреть иллюстрации).
И об этом же —
https://twitter.com/i/status/1283275125618442245
https://images.math.cnrs.fr/media/51/video.mp4
(отсюда — https://images.math.cnrs.fr/L-effet-Droste.html ; правда, там по-французски, но можно только посмотреть иллюстрации).
И об этом же —
https://twitter.com/i/status/1283275125618442245
Victor Kleptsyn
М
20:00
Математические байки
Н
Непрерывное математическое образование 15.07.2020 19:58:44
http://kvant.mccme.ru/1994/01/podkova_smejla.htm
к сегодняшнему 90-летию Смейла
пусть здесь будет статья в Кванте про подкову Смейла
к сегодняшнему 90-летию Смейла
пусть здесь будет статья в Кванте про подкову Смейла
Victor Kleptsyn
М
20:01
Математические байки
И вдогонку — брошюра ЛШСМ, заканчивающаяся как раз конструкцией подковы Смейла:
https://www.mccme.ru/free-books/dubna/ilyashenko-smale.pdf
https://www.mccme.ru/free-books/dubna/ilyashenko-smale.pdf
Victor Kleptsyn
20:15
Ну и — соответствующая глава из фильма "Хаос": https://www.chaos-math.org/ru/chaos-vi.html — вот тут показывают, как устроено символическое кодирование для неё: https://youtu.be/LktmWlabav0?t=363 (там есть русские субтитры)
Да, и более короткий ролик с подковой —
https://www.youtube.com/watch?v=SrJm6bkLuPs
Да, и более короткий ролик с подковой —
https://www.youtube.com/watch?v=SrJm6bkLuPs
Victor Kleptsyn
16 July 2020
М
19:50
Математические байки
In reply to this message
По случаю прошедшего юбилея Сергея Константиновича — "байка о трёхглавом драконе".
(У меня, конечно, ещё не закончен рассказ про ренормализацию, но давайте я его чуть-чуть отложу.)
(У меня, конечно, ещё не закончен рассказ про ренормализацию, но давайте я его чуть-чуть отложу.)
Victor Kleptsyn
19:51
Давайте зададимся тремя вопросами.
Вопрос 1: сколько есть разных способов разложить цикл длины n в произведение (n-1) транспозиции?
Вопрос 1: сколько есть разных способов разложить цикл длины n в произведение (n-1) транспозиции?
Victor Kleptsyn
19:51
Иными словами: мы расставили n статуй по стоящим вокруг площади постаментам, и только закончив работу, обнаружили, что перепутали, откуда надо было начинать. Статуя 1 стоит на постаменте 2, статуя 2 на постаменте 3, и так далее до статуи n, которая стоит на постаменте с подписью 1.
Надо их поставить на места; единственный доступный нам инструмент — "погрузчик", позволяющий поменять местами любые две статуи. Причём погрузчик нас просили вернуть как можно скорее — так что нужно обойтись минимальным числом операций.
Надо их поставить на места; единственный доступный нам инструмент — "погрузчик", позволяющий поменять местами любые две статуи. Причём погрузчик нас просили вернуть как можно скорее — так что нужно обойтись минимальным числом операций.
Victor Kleptsyn
19:52
Операций нам понадобится (n-1) — что, собственно, часть вопроса, но пока давайте в это поверим. Так вот, вопрос формулируется классическим комбинаторным образом: а сколькими способами мы сможем это сделать — поставить статуи на свои места за (n-1) применение погрузчика?
Victor Kleptsyn
19:53
Вопрос 2: сколько есть разных деревьев с n пронумерованными от 1 до n вершинами?
Рассмотрим наши пронумерованные вершины как вершины полного графа. Тогда дерево с этими вершинами — это остовное дерево такого графа. Поэтому тот же вопрос можно переформулировать как "сколько есть остовных деревьев в полном графе на n вершинах" ?
Рассмотрим наши пронумерованные вершины как вершины полного графа. Тогда дерево с этими вершинами — это остовное дерево такого графа. Поэтому тот же вопрос можно переформулировать как "сколько есть остовных деревьев в полном графе на n вершинах" ?
Victor Kleptsyn
19:54
Вопрос 3: сколько есть многочленов степени n с комплексными коэффициентами и с заданными (n-1) критическими значениями (т.е. значениями в критических точках — там, где производная обращается в 0)?
Victor Kleptsyn
19:58
Понятно, что в такой формулировке ответом будет "бесконечность", потому что если мы сдвинем многочлен, перейдя от P(z) к P(z+a), критические значения от этого не изменятся. Поэтому можно наложить условие, что коэффициент при z^{n-1} равен 0 (как раз любой многочлен в такой можно единственным образом сдвинуть).
И ещё наложим условие, что старший коэффициент равен 1. Опять-таки, любой многочлен с данными критическими значениями к такому виду приводится — только на этот раз заменой w=bz при правильном выборе b. А если никакого условия тут не наложить, то все такие замены нам из одного решения сделают бесконечное количество — что естественно, потому что у нас неизвестных коэффициентов пока n, а условий на критические значения (n-1).
И ещё наложим условие, что старший коэффициент равен 1. Опять-таки, любой многочлен с данными критическими значениями к такому виду приводится — только на этот раз заменой w=bz при правильном выборе b. А если никакого условия тут не наложить, то все такие замены нам из одного решения сделают бесконечное количество — что естественно, потому что у нас неизвестных коэффициентов пока n, а условий на критические значения (n-1).
Victor Kleptsyn
20:06
In reply to this message
Так что окончательная формулировка третьего вопроса — сколько есть многочленов вида
z^n + a_{n-2}z^{n-2} +...+a_1 z + a_0
с заданными (n-1) критическими значениями c_1,...,c_{n-1} ?
z^n + a_{n-2}z^{n-2} +...+a_1 z + a_0
с заданными (n-1) критическими значениями c_1,...,c_{n-1} ?
Victor Kleptsyn
20:07
In reply to this message
---
Вопросы сформулированы — и давайте сначала немного посчитаем, какими будут ответы при небольших n. Проще всего это сделать для второго вопроса.
Вопросы сформулированы — и давайте сначала немного посчитаем, какими будут ответы при небольших n. Проще всего это сделать для второго вопроса.
Victor Kleptsyn
20:08
Для n=2 единственное дерево на двух вершинах это отрезок, так что ответ 1.
Для n=3 это два последовательных отрезка — но важно, какая из трёх вершин в центре, поэтому мы получаем 3 варианта (можно сказать, что полный граф на трёх вершинах это треугольник, а мы выкидываем одну из его сторон).
Для n=4 деревьев без пометок два, это три последовательных отрезка и "лапа" из трёх отрезков с общей вершиной. В первом случае пометки можно расставить 12 способами (потому что 24/2 — подписываем всеми возможными способами, а потом вспоминаем, что дерево можно перевернуть), во втором 4 (единственное, что важно, это значение в центральной вершине; ну или 24/6, потому что отрезки из центра переставляются 3!=6 способами).
Итого 12+4=16 вариантов.
Для n=3 это два последовательных отрезка — но важно, какая из трёх вершин в центре, поэтому мы получаем 3 варианта (можно сказать, что полный граф на трёх вершинах это треугольник, а мы выкидываем одну из его сторон).
Для n=4 деревьев без пометок два, это три последовательных отрезка и "лапа" из трёх отрезков с общей вершиной. В первом случае пометки можно расставить 12 способами (потому что 24/2 — подписываем всеми возможными способами, а потом вспоминаем, что дерево можно перевернуть), во втором 4 (единственное, что важно, это значение в центральной вершине; ну или 24/6, потому что отрезки из центра переставляются 3!=6 способами).
Итого 12+4=16 вариантов.
Victor Kleptsyn
М
М
20:12
Математические байки
Наконец, для n=5 есть три разных дерева без пометок:
* четыре отрезка в линию — вершины можно подписать 60=120/2 способами;
* лапа-трилистник, у которой один из выходящих отрезков продолжается ещё одним; тут вершины можно подписать тоже 60=120/2 способами;
* одна точка, из которой выходят все четыре ребра; тут есть всего 5=120/24 способов подписать вершины (единственное, что имеет значение, это номер центральной вершины).
Итого 60+60+5=125.
* четыре отрезка в линию — вершины можно подписать 60=120/2 способами;
* лапа-трилистник, у которой один из выходящих отрезков продолжается ещё одним; тут вершины можно подписать тоже 60=120/2 способами;
* одна точка, из которой выходят все четыре ребра; тут есть всего 5=120/24 способов подписать вершины (единственное, что имеет значение, это номер центральной вершины).
Итого 60+60+5=125.
Victor Kleptsyn
20:12
125 это 5^3, и это ответ при n=5. Если после этого посмотреть на 16 как на ответ при n=4, то немедленно хочется записать 16=4^2.
Victor Kleptsyn
20:12
После чего последовательность ответов записывается как
2^0, 3^1, 4^2, 5^3,
и становится ясно, что ответом должно быть n^{n-2}.
2^0, 3^1, 4^2, 5^3,
и становится ясно, что ответом должно быть n^{n-2}.
Victor Kleptsyn
20:15
Этот ответ носит название формулы Кэли — и давайте я опять процитирую коллег:
Victor Kleptsyn
М
20:15
Математические байки
Н
Непрерывное математическое образование 12.04.2018 00:26:30
Ответ: n^{n-2}. У этой формулы Кэли много разных доказательств на любой вкус.
Есть чисто комбинаторные способы — например, код Прюфера (см. «Введение в дискретную математику» Ландо или почти любую книгу по графам) или биективное доказательство Joyal’а (можно найти в «Доказательствах из КНИГИ» или, скажем, вот).
Есть и использующие некоторую технику — например, вычисление производящей функции при помощи формулы обращения Лагранжа (см., например, «Лекции о производящих функциях» Ландо) или теорему о подсчете остовных деревьев при помощи определителя (см., например, те же «Доказательства из КНИГИ»).
Есть чисто комбинаторные способы — например, код Прюфера (см. «Введение в дискретную математику» Ландо или почти любую книгу по графам) или биективное доказательство Joyal’а (можно найти в «Доказательствах из КНИГИ» или, скажем, вот).
Есть и использующие некоторую технику — например, вычисление производящей функции при помощи формулы обращения Лагранжа (см., например, «Лекции о производящих функциях» Ландо) или теорему о подсчете остовных деревьев при помощи определителя (см., например, те же «Доказательства из КНИГИ»).
Victor Kleptsyn
М
20:16
Математические байки
Н
Непрерывное математическое образование 20.05.2019 00:08:36
а вот доказательство формулы Кэли для числа деревьев в… Квантике:
http://old.kvantik.com/art/files/pdf/2018-12.12-15.pdf
(К.Кохась. Как Бусенька разбирала новогоднюю ёлку)
http://old.kvantik.com/art/files/pdf/2018-12.12-15.pdf
(К.Кохась. Как Бусенька разбирала новогоднюю ёлку)
Victor Kleptsyn
М
20:20
Математические байки
Рассказ К.Кохася совершенно прекрасен — но мне, честно говоря, больше всего всё-таки нравится подход через матричную теорему о деревьях (Matrix Tree Formula): оказывается, что остовные деревья в любом графе можно посчитать как определитель некоторой (очень простой) матрицы. Но по этой дороге мы пройдём чуть позже — а пока давайте вернёмся к остальным вопросам.
Victor Kleptsyn
20:23
Следующий на очереди — вопрос 1. Опять-таки, давайте при небольших n посчитаем, сколькими способами цикл длины n можно разложить в произведение (n-1) транспозиции. Цикл у нас
(123...n)
(то есть 1 переходит в 2, 2 в 3,..., n в 1).
При n=2:
(12) = (12), вариант всего 1.
(123...n)
(то есть 1 переходит в 2, 2 в 3,..., n в 1).
При n=2:
(12) = (12), вариант всего 1.
Victor Kleptsyn
20:28
При n=3 не очень сложно проверить, что первой можно взять любую из трёх транспозиций, а вторая определяется однозначно:
(123)=(13)(12)=(23)(13)=(12)(23).
(123)=(13)(12)=(23)(13)=(12)(23).
Victor Kleptsyn
20:28
На всякий случай, я напомню: перестановки это отображения, поэтому при их умножении к элементам они применяются справа налево; то есть если
f=(23), а g=(13),
то при нахождении
fg(1)=f(g(1))
мы сначала находим g(1)=3, а потом f(g(1))=f(3)=2, как раз как нам и нужно.
f=(23), а g=(13),
то при нахождении
fg(1)=f(g(1))
мы сначала находим g(1)=3, а потом f(g(1))=f(3)=2, как раз как нам и нужно.
Victor Kleptsyn
20:30
Итак, при n=3 у нас есть 3 способа.
Victor Kleptsyn
20:33
При n=4 перебор проще всего организовать так. Запишем, что (1234) это произведение 3 транспозиций τ_1, τ_2, τ_3:
Victor Kleptsyn
20:34
Перенесём транспозицию τ_1 в левую часть (умножив на неё слева обе части равенства):
Victor Kleptsyn
20:42
После этого для каждого варианта τ_1 у нас будет вопрос, "сколькими способами произведение в левой части можно разбить в произведение двух транспозиций". И тут количество будет зависеть от τ_1.
Victor Kleptsyn
20:44
Если τ_1 переставляет два соседних по циклу числа, например, τ_1=(12), то в левой части мы увидим цикл длины 3:
(12)(1234)=(234).
И его, как мы уже знаем, можно представить в виде произведения соседних 3 способами.
А если τ_1=(13) или τ_1=(24), то произведение "разрезает" цикл в две транспозиции,
(13)(1234)=(12)(34)
и тут вариантов 2 — в каком порядке их перемножать.
Итого способов:
4*3+2*2=16.
(12)(1234)=(234).
И его, как мы уже знаем, можно представить в виде произведения соседних 3 способами.
А если τ_1=(13) или τ_1=(24), то произведение "разрезает" цикл в две транспозиции,
(13)(1234)=(12)(34)
и тут вариантов 2 — в каком порядке их перемножать.
Итого способов:
4*3+2*2=16.
Victor Kleptsyn
20:45
1,3,16 — что-то напоминает, не правда ли?
Victor Kleptsyn
20:50
Посмотрим теперь на третий вопрос, опять же, посчитав при небольших n.
Когда n=2, мы смотрим на квадратный трёхчлен
P(z)=z^2+a_0
с заданным критическим значением c. Такой трёхчлен единственен: a_0=c.
Когда n=2, мы смотрим на квадратный трёхчлен
P(z)=z^2+a_0
с заданным критическим значением c. Такой трёхчлен единственен: a_0=c.
Victor Kleptsyn
20:52
Когда n=3, мы смотрим на кубический многочлен
P(z)=z^3+pz+q
(я обозначу p=a_1 и q=a_0, чтобы формулы легче читались).
P(z)=z^3+pz+q
(я обозначу p=a_1 и q=a_0, чтобы формулы легче читались).
Victor Kleptsyn
20:53
Его критические точки это корни уравнения P'(z)=0, т. е.
3z^2+p=0.
То есть это
3z^2+p=0.
То есть это
Victor Kleptsyn
20:57
P(z)=z(z^2+p)+q;
в скобке в обоих случаях стоит (2p/3), поэтому критические значения это
в скобке в обоих случаях стоит (2p/3), поэтому критические значения это
Victor Kleptsyn
20:57
То есть a_0=q определяется однозначно как полусумма c_1 и c_2.
Victor Kleptsyn
20:58
А вот для p нам понадобится кубический корень, потому что
(c_1-c_2)^2 = const * p^3
(c_1-c_2)^2 = const * p^3
Victor Kleptsyn
20:59
Поэтому таких кубических многочленов 3.
Victor Kleptsyn
21:01
Конечно же, ответы на эти три вопроса совпадают не случайно (точно так же, как рассказ я не случайно назвал "байка о трёхглавом драконе").
На самом деле это — один и тот же вопрос. А вот почему, я расскажу в следующий раз.
На самом деле это — один и тот же вопрос. А вот почему, я расскажу в следующий раз.
Victor Kleptsyn
18 July 2020
М
20:26
Математические байки
О
Общий знаменатель 18.07.2020 10:36:55
Из предисловия к материалам общематематического семинара "Глобус":
Всего пару столетий назад жили люди, понимавшие всю существовавшую в то время математику, да пожалуй и физику. Сто лет назад –– почти всю. Сейчас, как бы лучшие ученые мира ни стремились уподобиться в этом величайшим из своих
предшественников, это стало совершенно невозможно. Более того, даже математики, специализирующиеся в той или иной области, зачастую совсем не отдают себе отчета в том, чем занимаются их коллеги. Как ни печально, разобщение и специализация –– одна из тенденций развития всей современной науки, и было бы наивно надеяться, что математика станет исключением из общего правила.
И вот, именно поэтому, у профессоров Независимого Московского университета возникло заведомо безнадежное желание с этой тенденцией побороться
https://www.mccme.ru/free-books/globus/globus1.pdf
Всего пару столетий назад жили люди, понимавшие всю существовавшую в то время математику, да пожалуй и физику. Сто лет назад –– почти всю. Сейчас, как бы лучшие ученые мира ни стремились уподобиться в этом величайшим из своих
предшественников, это стало совершенно невозможно. Более того, даже математики, специализирующиеся в той или иной области, зачастую совсем не отдают себе отчета в том, чем занимаются их коллеги. Как ни печально, разобщение и специализация –– одна из тенденций развития всей современной науки, и было бы наивно надеяться, что математика станет исключением из общего правила.
И вот, именно поэтому, у профессоров Независимого Московского университета возникло заведомо безнадежное желание с этой тенденцией побороться
https://www.mccme.ru/free-books/globus/globus1.pdf
Victor Kleptsyn
М
20:28
Математические байки
In reply to this message
А вот оглавление первого выпуска, которое я тут уже выкладывал.
Victor Kleptsyn
20 July 2020
М
15:55
Математические байки
Лекция начинается через ~5 минут
Victor Kleptsyn
М
15:55
Математические байки
Н
Непрерывное математическое образование 19.07.2020 19:28:15
К завтрашней лекции Гаянэ Паниной две задачи:
1) всякая плоская фигура может быть разделена двумя прямолинейными разрезами на четыре равные по площади части;
2) не всякая плоская фигура может быть разделена тремя прямолинейными разрезами на семь равных по площади частей.
1) всякая плоская фигура может быть разделена двумя прямолинейными разрезами на четыре равные по площади части;
2) не всякая плоская фигура может быть разделена тремя прямолинейными разрезами на семь равных по площади частей.
Victor Kleptsyn
М
16:10
Математические байки
Первый (самый простой) вопрос из лекции Гаянэ: есть N красных и N зелёных точек в общем положении на плоскости. Всегда ли их можно разбить на пары попарно непересекающимися отрезками?
Victor Kleptsyn
16:14
Решение 1 (стандартное): принцип крайнего. Разобьём как-нибудь, если какие-то два отрезка пересеклись, то "перещёлкнем" их, поменяв пары. Тогда сумма их длин уменьшится (неравенство треугольника). Значит, сумма длин всех отрезков за каждую операцию уменьшается, а число способов разбить на пары конечно. Поэтому то разбиение, которое минимизирует сумму длин, нас точно устроит.
Victor Kleptsyn
16:15
In reply to this message
А Гаянэ показывает другое решение — можно найти прямую, по обе стороны от почти одинаковое число точек каждого из цветов. И дальше можно запустить индукцию — сгруппировав по отдельности точки слева и справа от прямой.
Victor Kleptsyn
16:15
А это деление — это аналог теоремы о блинах:
Victor Kleptsyn
16:17
А теорема о бутерброде применяется для аналогичного вопроса в размерности 3 —
Victor Kleptsyn
М
16:43
Математические байки
... и вот уже в задаче об одновременном делении двух тел двумя плоскостями возникает класс Эйлера ...
Victor Kleptsyn
23 July 2020
М
11:22
Математические байки
In reply to this message
Продолжим про ренормализацию и универсальность?
Victor Kleptsyn
11:31
И давайте я напомню кусочек истории про логистическое отображение. Это отображение
x-> λx(1-x).
Его очень естественно использовать для популяционной динамики: если в этом году популяция равна x — то в следующем будет λx из-за размножения, "подправленное" на -λx^2 из-за того, что когда кроликов/белок/рыб/кузнечиков много, они мешают друг другу, съедая общую кормовую базу.
Коэффициент перед x^2 можно сделать любым — это вопрос масштаба/единиц измерения; тут масштаб выбран таким, чтобы 1 было тем максимумом, до которого на следующий год вообще хоть кто-нибудь доживёт.
x-> λx(1-x).
Его очень естественно использовать для популяционной динамики: если в этом году популяция равна x — то в следующем будет λx из-за размножения, "подправленное" на -λx^2 из-за того, что когда кроликов/белок/рыб/кузнечиков много, они мешают друг другу, съедая общую кормовую базу.
Коэффициент перед x^2 можно сделать любым — это вопрос масштаба/единиц измерения; тут масштаб выбран таким, чтобы 1 было тем максимумом, до которого на следующий год вообще хоть кто-нибудь доживёт.
Victor Kleptsyn
11:40
В 1976 году в Nature появилась статья Р. Мэя (https://www.nature.com/articles/261459a0 ), в которой он его популяризизировал — в том числе, обсуждая каскад бифуркаций удвоения периода — и вскоре "началось".
Кстати, тоже чисто историческое. В этой статье два рисунка (рис. 2 и 3) — "до" и "после" бифуркации удвоения периода — поменяли местами (но оставив на месте подписи). Представляю, как автору должно было быть обидно...
Кстати, тоже чисто историческое. В этой статье два рисунка (рис. 2 и 3) — "до" и "после" бифуркации удвоения периода — поменяли местами (но оставив на месте подписи). Представляю, как автору должно было быть обидно...
Victor Kleptsyn
11:47
На этой — известной — диаграмме по оси абсцисс отложен параметр λ, а по оси ординат — "предельный режим", на который система при данном λ выходит.
Victor Kleptsyn
11:48
Так, при λ<=1 популяция просто вымирает; при λ от 1 до 3 выходит на положение равновесия:
Victor Kleptsyn
11:50
In reply to this message
При λ=3 происходит бифуркация удвоения периода, потом ещё одна, потом ещё одна...
Victor Kleptsyn
11:53
И они учащаются как геометрическая прогрессия: есть предел отношений длин отрезков параметров, на которых предельный режим это орбита периода 2^k:
Victor Kleptsyn
12:03
Так вот, во-первых, можно взять другое семейство унимодальных ("похожих на шапку") отображений. Например, можно взять отображения отрезка [0,π],
x -> μ sin x.
Опять же, при μ<1 популяция вымирает, при μ=π (когда образ это весь отрезок) система уже точно в "полностью хаотическом" режиме, и увеличивая μ, мы сначала наткнёмся на каскад бифуркаций удвоения.
x -> μ sin x.
Опять же, при μ<1 популяция вымирает, при μ=π (когда образ это весь отрезок) система уже точно в "полностью хаотическом" режиме, и увеличивая μ, мы сначала наткнёмся на каскад бифуркаций удвоения.
Victor Kleptsyn
12:04
Опять же, длины отрезков параметров, при которых система выходит на орбиту периода 2^n, "учащаются" в геометрической прогрессии:
Victor Kleptsyn
12:06
Так вот — константа δ тут та же самая, хотя семейство совершенно другое (одно полиномиальное, другое трансцендентное). И это явление называется универсальностью Фейгенбаума-Куле-Трессера.
Victor Kleptsyn
12:13
Во-вторых: можно начать увеличивать картинку множества Мандельброта вокруг той точки c_*, куда накапливаются бифуркации удвоения периода.
Victor Kleptsyn
12:16
(каждая следующая картинка — увеличенная примерно в те самые 4.6 раз, это вовсе не одна и та же картинка — что можно увидеть по тому, что меняются цвета)
Victor Kleptsyn
12:17
Соответственно, второй вопрос — а почему картинки так похожи? Ведь итерировать параметр c, казалось бы, нельзя...
Victor Kleptsyn
12:20
И ответом на оба эти вопроса является ренормализация.
Victor Kleptsyn
12:22
Вообще, ренормализация — ситуация, когда мы сводим задачу из некоторого класса к другой задаче из того же класса. Казалось бы, мы на этом ничего не выигрываем (обычно, как исходная задача не решалась, так и новая не решается) — зато вот итерируя такие сведения, результаты добыть получается.
Victor Kleptsyn
12:29
Давайте пока посмотрим на вещественную картину; пусть у нас есть "одношапочное" отображение —
Victor Kleptsyn
12:30
Если "шапочка" не слишком плоская, то у него будет неподвижная точка с отрицательным мультипликатором. Давайте возведём его в квадрат — тогда одна итерация нового отображения соответствует двум итерациям старого:
Victor Kleptsyn
12:33
Но у нового отображения можно (если "шапочка" была не слишком "высокая") найти сохраняющийся подотрезок:
Victor Kleptsyn
12:34
И на нём отображение опять унимодальное — растянув отрезок обратно на [0,1], мы получаем отображение того же класса:
Victor Kleptsyn
12:37
Вот так работает отображение ренормализации. Оно определено не всегда: если шапочка была слишком плоской, то мультипликатор в неподвижной точке будет положительным, а если слишком высокой, то посередине отображение f^2 вылезет за красный отрезок.
Victor Kleptsyn
12:39
Но — это уже конкретное отображение, пусть и определённое на бесконечномерном пространстве всех унимодальных отображений (ну, или всех с неравенством на производную Шварца — давайте детали я замету под ковёр).
Victor Kleptsyn
12:41
И его можно исследовать. Так вот — картинка с каскадом бифуркаций удвоения периода в его терминах проговаривается: ведь f будет точкой, где происходит бифуркация от орбиты периода 2^n к орбите периода 2^{n+1} тогда и только тогда, когда R^n(f) будет точкой, где происходит простейшее удвоение периода от неподвижной точки к орбите периода 2.
Victor Kleptsyn
12:51
Оказывается, что у него есть неподвижная точка. И эта точка гиперболическая: если в ней R линеаризовать, то все собственные значения, кроме одного, будут по модулю меньше 1 — что будет соответствовать сжатию; а одно будет больше 1.
Поэтому есть подмногообразие коразмерности 1, по которому происходит приближение к этой неподвижной точке — и её "неустойчивая сепаратриса":
Поэтому есть подмногообразие коразмерности 1, по которому происходит приближение к этой неподвижной точке — и её "неустойчивая сепаратриса":
Victor Kleptsyn
12:58
Соответственно, если мы нарисуем на этой картинке однопараметрическое семейство отображений (логистическое, или \mu \sin(πx), или ещё какое-нибудь), то предельной точкой каскада бифуркаций удвоения будет момент, когда это семейство пересечёт то самое устойчивое подмногообразие:
Victor Kleptsyn
13:00
Когда мы будем его ренормализовывать — сама точка пересечения будет приближаться к неподвижной, а семейство растягиваться в "вертикальном" направлении, и будет становиться всё ближе к неустойчивой сепаратрисе:
Victor Kleptsyn
М
14:53
Математические байки
И отсюда следует ответ про универсальность — а заодно объяснение того, что же такое за постоянная Фейгенбаума δ. Все семейства, трансверсально ("под ненулевым углом") пересекающие устойчивое многообразие, последовательность ренормализаций делает всё ближе и ближе к неустойчивой сепаратрисе — на которой рядом с неподвижной точкой происходит растяжение в число раз, равное (при правильном выборе координат) соответствующему собственному значению. Вот это и есть асимптотический знаменатель "учащения бифуркаций" — δ это просто неустойчивое собственное значение R!
Victor Kleptsyn
14:56
Давайте я добавлю к этому картинку из слайдов Шишикуры (https://www.math.univ-toulouse.fr/adrien2008/Slides/Shishikura.pdf ) —
Victor Kleptsyn
14:59
И скажу, что ренормализация не обязательно должна происходить за две итерации. Может быть, интервал, на который мы захотим вернуться, возвращается на себя за три итерации. А может быть, за 5...
А ещё можно объединить все эти отображения ренормализации (R_2, R_3, ...) — и получить "подкову ренормализации" (renormalization horseshoe)
А ещё можно объединить все эти отображения ренормализации (R_2, R_3, ...) — и получить "подкову ренормализации" (renormalization horseshoe)
Victor Kleptsyn
15:01
Да — коллеги тут мне говорят, что от условия про отрицательную производную Шварца давно уже как избавились, и это работа О. Козловского в Annals, "Getting rid of the negative Schwarzian derivative condition":
https://www.emis.de/journals/Annals/152_3/kozlovsk.pdf
https://www.emis.de/journals/Annals/152_3/kozlovsk.pdf
Victor Kleptsyn
15:05
Давайте я ещё порекламирую статью М. Любича в Notices AMS, "The Quadratic Family as a Qualitatively Solvable Model of Chaos" —
https://www.ams.org/journals/notices/200009/fea-lyubich.pdf
https://www.ams.org/journals/notices/200009/fea-lyubich.pdf
Victor Kleptsyn
15:05
Рисунок 8 оттуда нам уже знаком:
Victor Kleptsyn
15:10
А вот другая статья М. Любича, Feigenbaum-Coullet-Tresser universality and Milnor’s Hairiness Conjecture, Annals of Mathematics, 1999 : https://www.emis.de/journals/Annals/149_2/lyubich.pdf
Victor Kleptsyn
15:15
Первая часть названия понятна; а вот о чём говорит вторая:
Victor Kleptsyn
15:18
Мы видели на картинках выше, что множество Мандельброта под увеличением действительно становится всё более "волосатым". А вот тут эти картинки свели в одну анимированную гифку:
https://commons.wikimedia.org/wiki/File:Zoom_About_Feigenbaum_Point_In_The_Mandelbrot_Set_Showing_Hairiness.gif
https://commons.wikimedia.org/wiki/File:Zoom_About_Feigenbaum_Point_In_The_Mandelbrot_Set_Showing_Hairiness.gif
Victor Kleptsyn
15:19
In reply to this message
Выглядит, как типичная картинка из компьютерной игры, когда надо показать, что "тьма спустилась на мир".
Victor Kleptsyn
М
17:44
Математические байки
Чтобы закончить с логистическим отображением — мы пока обсуждали устойчивые периодические орбиты. Но предельным режимом бывают не только они.
Victor Kleptsyn
17:44
Так, если взять максимально возможное значение \lambda=4, то получается многочлен, отличающийся от многочлена Чебышева заменой координат. Если
T_2(y)=2y^2 -1
переводит cos(a) в cos(2a), то замена x=(1-y)/2 превращает его итерации в итерации
f(x)=4x(1-x).
Ну или можно было сразу сказать, что
4x(1-x)
переводит sin^2(b) в sin^2(2b).
T_2(y)=2y^2 -1
переводит cos(a) в cos(2a), то замена x=(1-y)/2 превращает его итерации в итерации
f(x)=4x(1-x).
Ну или можно было сразу сказать, что
4x(1-x)
переводит sin^2(b) в sin^2(2b).
Victor Kleptsyn
17:59
Так или иначе — итерации при \lambda=4 получаются из "удвоения угла" на окружности a->2a. Его динамика хаотична — а типичная орбита оказывается распределена в соответствии с мерой, которая в b-координате является мерой Лебега, а в x-координате — её образом при проекции
b->sin^2 b =x
(соответственно, будет абсолютно непрерывной )
b->sin^2 b =x
(соответственно, будет абсолютно непрерывной )
Victor Kleptsyn
18:05
В видео Veritasium, которое я уже цитировал, автор упоминает про генератор псевдослучайных чисел —
https://youtu.be/ovJcsL7vyrk?t=322
https://youtu.be/ovJcsL7vyrk?t=322
Victor Kleptsyn
18:07
Может быть, это связано как раз с этим; кстати — после этого рассказа видео должно быть совсем легко смотреть.
Victor Kleptsyn
18:08
Так вот — хаотическое поведение это вовсе не изолированный случай \lambda=4. Напротив того, параметры \lambda, при которых образуется такое "хаотическое" поведение, образуют множество положительной меры.
Victor Kleptsyn
18:11
И это довольно интересно: ведь параметры, при которых происходит "сваливание в периодическую орбиту", образуют открытое плотное множество. То есть где угодно на отрезке параметров есть маленький интервал, отвечающий тому, что всё стремится к какой-то притягивающей периодической орбите.
(Кстати — помните ведь, что для квадратичных отображений такая орбита может быть только одна, потому что к ней обязательно стремятся образы единственной критической точки?)
(Кстати — помните ведь, что для квадратичных отображений такая орбита может быть только одна, потому что к ней обязательно стремятся образы единственной критической точки?)
Victor Kleptsyn
18:12
Так вот — несмотря на то, что множество гиперболических (всё стремится к устойчивой периодической орбите) параметров открытое и плотное, после того, как все эти интервалы выкинуты, ещё что-то остаётся!
Victor Kleptsyn
18:16
Зато в объединении — "гиперболические" и "хаотические" параметры уже покрывают почти весь отрезок (с точностью до меры 0).
Victor Kleptsyn
18:17
Я процитирую слайд из другого доклада Шишикуры (https://www.impan.pl/konferencje/bcc/2018/18-juliasets/shishikura-bedlewo-juliasets.pdf ) —
Victor Kleptsyn
18:18
И на этом, наверное, этот рассказ можно завершить.
Victor Kleptsyn
24 July 2020
М
21:15
Математические байки
Н
Непрерывное математическое образование 20.07.2020 22:19:40
видеозапись: https://youtu.be/xRRNCuxLEyQ
Victor Kleptsyn
М
21:18
Математические байки
В лекции Гаянэ Паниной упоминалась кривая Веронезе — кривая в R^n, задаваемая параметрически как
(t,t^2,t^3,...,t^n).
Я в первый раз о ней узнал на одном из курсов в Независимом — где с её помощью строился совершенно прекрасный пример.
Вот на плоскости, если у выпуклого многоугольника любые две вершины соединены ребром, то это треугольник.
В пространстве, если у выпуклого (неплоского) многогранника любые две вершины соединены ребром — то это тетраэдр. (И это, кстати, уже не совсем тривиально!)
А что будет в старших размерностях?
(t,t^2,t^3,...,t^n).
Я в первый раз о ней узнал на одном из курсов в Независимом — где с её помощью строился совершенно прекрасный пример.
Вот на плоскости, если у выпуклого многоугольника любые две вершины соединены ребром, то это треугольник.
В пространстве, если у выпуклого (неплоского) многогранника любые две вершины соединены ребром — то это тетраэдр. (И это, кстати, уже не совсем тривиально!)
А что будет в старших размерностях?
Victor Kleptsyn
21:20
Так вот — уже в размерности 4 можно предъявить выпуклый многогранник с любым числом вершин, такой, что любые две соединены ребром.
Victor Kleptsyn
21:21
А именно — давайте возьмём любые n точек на кривой Веронезе в R^4, отвечающие параметрам t_1,t_2,...,t_n.
Victor Kleptsyn
21:26
Их выпуклая оболочка и будет искомым многогранником. Действительно: посмотрим на многочлен
P(t) = (t-t_i)^2 (t-t_j)^2.
Если в нём раскрыть скобки, то получится линейная комбинация 1, t ,..., t^4:
P(t)=a_0+a_1 t +...+a_4 t^4.
Превратим её в линейную функцию:
L(x_1,...,x_4)=a_0+a_1 x_1+...+a_4 x_4.
Эта функция равна 0 в вершинах с t=t_i и t=t_j, и положительна во всех остальных. Значит, эти две вершины лежат на гиперплоскости L=0, а все остальные — вне неё в одном и том же полупространстве L>0.
P(t) = (t-t_i)^2 (t-t_j)^2.
Если в нём раскрыть скобки, то получится линейная комбинация 1, t ,..., t^4:
P(t)=a_0+a_1 t +...+a_4 t^4.
Превратим её в линейную функцию:
L(x_1,...,x_4)=a_0+a_1 x_1+...+a_4 x_4.
Эта функция равна 0 в вершинах с t=t_i и t=t_j, и положительна во всех остальных. Значит, эти две вершины лежат на гиперплоскости L=0, а все остальные — вне неё в одном и том же полупространстве L>0.
Victor Kleptsyn
21:27
И потому эти две вершины это действительно вершины выпуклой оболочки, причём соединённые ребром.
А начиная с размерности 6, точно так же можно построить выпуклый многогранник, у которого любые три вершины соединены двумерной гранью-треугольником. И так далее.
А начиная с размерности 6, точно так же можно построить выпуклый многогранник, у которого любые три вершины соединены двумерной гранью-треугольником. И так далее.
Victor Kleptsyn
21:32
А завтра в "Математических вечерах ЛШСМ" будет лекция Окунькова!
Victor Kleptsyn
М
21:32
Математические байки
Н
Непрерывное математическое образование 24.07.2020 17:26:42
http://book.etudes.ru/toc/patternhappen/
«Наполненные гелием воздушные шары в моём детстве были редкостью и завораживали нас своим стремлением ввысь. Теперь, конечно, ими никого не удивишь, но всё равно грустно смотреть вслед упущенному и стремительно взмывающему вверх шару. Самое время поразмыслить о случайности и закономерности…»
пусть здесь будет небольшой текст Андрея Окунькова из «Математической составляющей»
«Наполненные гелием воздушные шары в моём детстве были редкостью и завораживали нас своим стремлением ввысь. Теперь, конечно, ими никого не удивишь, но всё равно грустно смотреть вслед упущенному и стремительно взмывающему вверх шару. Самое время поразмыслить о случайности и закономерности…»
пусть здесь будет небольшой текст Андрея Окунькова из «Математической составляющей»
Victor Kleptsyn
26 July 2020
М
13:41
Математические байки
Завтра в "Математических вечерах ЛШСМ" будет лекция Этьена Жиса; если (надеюсь!) не будет никаких накладок, то я буду её синхронно переводить на русский.
А пока — в качестве рекламы хочется вспомнить его лекцию в ЛШСМ-2008:
http://www.mathnet.ru/php/presentation.phtml?option_lang=rus&presentid=228
Она начинается с прекрасного сюжета про соприкасающиеся окружности — который я, собственно, тогда от Этьена и узнал.
А пока — в качестве рекламы хочется вспомнить его лекцию в ЛШСМ-2008:
http://www.mathnet.ru/php/presentation.phtml?option_lang=rus&presentid=228
Она начинается с прекрасного сюжета про соприкасающиеся окружности — который я, собственно, тогда от Этьена и узнал.
Victor Kleptsyn
13:43
Вот здесь Этьен говорит: зачастую, если вы просите кого-то нарисовать кривую и множество соприкасающихся с ней окружностей в всех точках, вы получаете что-нибудь такое:
Victor Kleptsyn
13:44
Так вот — это абсолютно неверно!
Victor Kleptsyn
13:45
Потому что пока радиус кривизны меняется монотонно — соприкасающиеся окружности лежат одна внутри другой и не пересекаются!
Вот как выглядит их набор для спирали:
Вот как выглядит их набор для спирали:
Victor Kleptsyn
13:49
Сама спираль, кстати, могла бы быть и не нарисована: мы бы всё равно её увидели из-за того, как на ней семейство окружностей сгущается (и это не случайность!).
Victor Kleptsyn
М
14:25
Математические байки
Давайте я пока оставлю тут ссылку на статью Жиса, Табачникова и Тиморина (Osculating curves: around the Tait-Kneser theorem, Math. Intelligencer 35 (2013)) — http://perso.ens-lyon.fr/ghys/articles/osculatingcurves.pdf — и упомяну заодно лекцию 10 ("Вокруг четырёх вершин") из "Математического дивертисмента" Фукса-Табачникова
Victor Kleptsyn
14:26
Но это было в качестве рекламы — а завтра Этьен будет рассказывать совсем о другом!
Victor Kleptsyn
29 July 2020
М
13:19
Математические байки
Меньше, чем через три часа, в "Математических вечерах ЛШСМ" ( https://www.mccme.ru/dubna/lect2020/ ) лекция Александра Логунова, "Гармонические функции и парадоксы вокруг теоремы Лиувилля".
Victor Kleptsyn
13:21
А ещё — из позавчерашней лекции Этьена Жиса, её отправная точка: теорема Концевича "с билета на метро".
Victor Kleptsyn
13:22
Как-то раз, много лет назад, Этьен Жис и Максим Концевич сидели рядом на скучном заседании какой-то комиссии, и Концевич что-то писал на маленьком кусочке бумаги. В какой-то момент он передал Этьену билет на (парижское) метро, на котором был рисунок и одно-единственное слово, "impossible" = "невозможно".
Victor Kleptsyn
13:23
Это и была теорема Концевича.
Вот что она утверждает, если её сформулировать более развернуто. Предположим, что у нас есть несколько многочленов, обращающихся в ноль в точке x=0:
Вот что она утверждает, если её сформулировать более развернуто. Предположим, что у нас есть несколько многочленов, обращающихся в ноль в точке x=0:
Victor Kleptsyn
13:24
Тогда есть порядок, в котором их графики идут слева от 0 (достаточно близко к 0, чтобы там не было других точек пересечения), а есть — порядок справа от 0. Поэтому возникает перестановка "прохода вдоль графиков" — переводящая порядок слева от 0 в порядок справа от 0.
Victor Kleptsyn
13:25
Теорема Концевича: 4 графика многочленов не могут образовывать картинку с билета на метро — иными словами, перестановка
1-> 3,
2-> 1,
3-> 4,
4-> 2
не реализуется никакой четвёркой многочленов.
1-> 3,
2-> 1,
3-> 4,
4-> 2
не реализуется никакой четвёркой многочленов.
Victor Kleptsyn
13:25
Конечно, такой же вопрос можно задавать для любых n различных многочленов — и наоборот, для любой перестановки n элементов спрашивать, реализуется ли она. Так, тройка многочленов x^2,0,-x^2 реализует тождественную перестановку, а тройка x,0,-x — переворачивающую перестановку
123 -> 321.
123 -> 321.
Victor Kleptsyn
13:27
Вопрос: какие перестановки таким образом реализуются?
Для n=1,2,3 — все возможные. Это простое упражнение — а вот картинка из книги Жиса "A Singular Mathematical Promenade":
Для n=1,2,3 — все возможные. Это простое упражнение — а вот картинка из книги Жиса "A Singular Mathematical Promenade":
Victor Kleptsyn
13:28
Для n=4 же есть ровно две невозможные перестановки: та, которую Концевич показывал Жису на билете в метро, и её обратная (соответствующая зеркальному отражению картинки).
Victor Kleptsyn
13:28
А что будет для произвольного n?
Теорема: Перестановка n элементов реализуется некоторым набором из n полиномов тогда и только тогда, когда никакие четыре точки не переставляются ни одним из двух запрещённых способов.
Теорема: Перестановка n элементов реализуется некоторым набором из n полиномов тогда и только тогда, когда никакие четыре точки не переставляются ни одним из двух запрещённых способов.
Victor Kleptsyn
30 July 2020
М
16:48
In reply to this message
Из статьи Этьена Жиса "Intersecting curves
(variation on an observation of Maxim Kontsevich)" — http://perso.ens-lyon.fr/ghys/articles/intersectingcurves.pdf
(variation on an observation of Maxim Kontsevich)" — http://perso.ens-lyon.fr/ghys/articles/intersectingcurves.pdf
Victor Kleptsyn
16:52
Кстати, вышла эта статья в номере American Mathematical Monthly, посвящённом "евро-Дубне" — европейской летней школе-близнецу ЛШСМ, проходившей в Бремене и в Лионе.
Поэтому у этого номера бременские музыканты на обложке:
https://www.jstor.org/stable/10.4169/amer.math.monthly.120.03.232?seq=1
Поэтому у этого номера бременские музыканты на обложке:
https://www.jstor.org/stable/10.4169/amer.math.monthly.120.03.232?seq=1
Victor Kleptsyn
16:56
Доказать теорему Концевича очень просто:
Доказательство. От противного — пусть такая четвёрка полиномов существует. Сразу можно предположить, что f_1=0 (просто вычтя его из остальных).
Определение. Нормирование (valuation) v(P) многочлена P — это порядок его корня в нуле, иными словами, самая младшая степень, коэффициент при которой отличен от нуля.
Это определение очень полезно: если нормирование у многочлена чётно, то он справа и слева от нуля одного знака, а если нечётно, то разных. А ещё легко увидеть, что верно вот такое вспомогательное утверждение:
Лемма. Если |P|>|Q| в левой или правой окрестности нуля, то v(P)<=v(Q).
(Собственно, очень логично: чем выше порядок нуля, тем меньше в малой окрестности должен быть многочлен.)
Доказательство. От противного — пусть такая четвёрка полиномов существует. Сразу можно предположить, что f_1=0 (просто вычтя его из остальных).
Определение. Нормирование (valuation) v(P) многочлена P — это порядок его корня в нуле, иными словами, самая младшая степень, коэффициент при которой отличен от нуля.
Это определение очень полезно: если нормирование у многочлена чётно, то он справа и слева от нуля одного знака, а если нечётно, то разных. А ещё легко увидеть, что верно вот такое вспомогательное утверждение:
Лемма. Если |P|>|Q| в левой или правой окрестности нуля, то v(P)<=v(Q).
(Собственно, очень логично: чем выше порядок нуля, тем меньше в малой окрестности должен быть многочлен.)
Victor Kleptsyn
16:59
In reply to this message
Применим эту лемму: слева от нуля
|f_4|>|f_3|>|f_2|
(напомним, f_1=0), поэтому
v(f_4)<=v(f_3)<=v(f_2).
С другой стороны, справа от нуля |f_2|>|f_4|, поэтому
v(f_2)<=v(f_4),
значит, все три нормирования совпадают.
|f_4|>|f_3|>|f_2|
(напомним, f_1=0), поэтому
v(f_4)<=v(f_3)<=v(f_2).
С другой стороны, справа от нуля |f_2|>|f_4|, поэтому
v(f_2)<=v(f_4),
значит, все три нормирования совпадают.
Victor Kleptsyn
17:00
Но f_2 меняет знак при переходе через ноль, значит, его нормирование нечётное. А f_3 сохраняет, значит, его нормирование чётное. Но одно и то же число не может быть и чётным, и нечётным одновременно!
Victor Kleptsyn
М
17:29
Математические байки
In reply to this message
Для произвольного n — стрелка в одну сторону в теореме Жиса очевидна. А вот почему запрет на четвёрки единственно необходимый, надо смотреть.
Давайте я об этом сюжете скажу ещё буквально пару слов — и отошлю к выложенной записи лекции и к книге Жиса "A Singular Mathematical Promenade", английский текст которой, кстати, выложен в открытом доступе.
Давайте я об этом сюжете скажу ещё буквально пару слов — и отошлю к выложенной записи лекции и к книге Жиса "A Singular Mathematical Promenade", английский текст которой, кстати, выложен в открытом доступе.
Victor Kleptsyn
М
17:30
Математические байки
Н
Непрерывное математическое образование 27.07.2020 13:34:21
к сегодняшней лекции Этьена Жиса напомним про книгу A Singular Mathematical Promenade — английская версия доступна на архиве ( https://arxiv.org/abs/1612.06373 ), русское издание готовится к выходу
Victor Kleptsyn
17:30
Н
Непрерывное математическое образование 30.07.2020 17:04:10
https://youtu.be/dUqJIdhICDQ
см. тж. рассказ в «математических байках», https://t.me/mathtabletalks/2710 и далее
см. тж. рассказ в «математических байках», https://t.me/mathtabletalks/2710 и далее
Victor Kleptsyn
М
17:32
Математические байки
Ссылка на видео лекции, конечно, есть и на https://www.mccme.ru/dubna/lect2020/ ; кстати, видео вчерашней лекции Александра Логунова тоже уже выложено (как и его слайды) — см. https://youtu.be/wuOqN-jfie4
Victor Kleptsyn
17:46
Да — в качестве рекламы, первый слайд лекции Логунова:
Victor Kleptsyn
17:49
Понятно, что угол, под которым из точки X виден отрезок AB, это аргумент отношения ((X-B)/(X-A)), иными словами, мнимая часть логарифма этого отношения. А мнимая часть комплексно-дифференцируемой функции гармонична — и остаётся применить теорему о среднем.
Но красиво — такое чисто геометрическое утверждение. :)
Но красиво — такое чисто геометрическое утверждение. :)
Victor Kleptsyn
М
18:06
Математические байки
Но давайте я вернусь к лекции и к книге Жиса.
Вообще, можно спросить, как описывать порождаемую какими-то многочленами перестановку. И тут ответ очень простой и логичный: давайте их сгруппируем сначала по производной в нуле (или по коэффициенту при x), потом внутри одной группы по коэффициенту при x^2, и так далее. Тогда (под)группы, отличающиеся в первый раз в нечётной степени, меняют свой порядок на обратный, а группы, отличающиеся в чётной, его сохраняют.
Вообще, можно спросить, как описывать порождаемую какими-то многочленами перестановку. И тут ответ очень простой и логичный: давайте их сгруппируем сначала по производной в нуле (или по коэффициенту при x), потом внутри одной группы по коэффициенту при x^2, и так далее. Тогда (под)группы, отличающиеся в первый раз в нечётной степени, меняют свой порядок на обратный, а группы, отличающиеся в чётной, его сохраняют.
Victor Kleptsyn
18:07
Картинка из лекции —
Victor Kleptsyn
18:09
Если действовать буквально так, то на каких-то "этажах" может статься, что подразбивать не понадобится; а подразбиения на уровнях одинаковой чётности, между которыми ничего не происходит, можно объединять. Скажем, если у нас
P_1=x+x^3, P_2=x+2x^3, P_3=2x,
то уровень x^2 ничего не добавляет, и порядок всех этих трёх многочленов меняется на обратный.
P_1=x+x^3, P_2=x+2x^3, P_3=2x,
то уровень x^2 ничего не добавляет, и порядок всех этих трёх многочленов меняется на обратный.
Victor Kleptsyn
18:10
И если это учесть — получается, что перестановке сопоставляется (корневое плоское) дерево, у которого каждая вершина имеет либо 0 потомков, либо не меньше 2.
Victor Kleptsyn
18:14
Только ещё есть вопрос о том, что же происходит на первом уровне (самая младшая степень, в которой отличаются многочлены, чётная или нечётная), поэтому число возможных перестановок будет вдвое больше, чем число таких деревьев.
Victor Kleptsyn
18:16
Таких деревьев с n листьями при n=1,2,3,4 будет 1,1,3 и 11 соответственно — что как раз соответствует 1,2,6,22=24-2 реализующимся перестановкам (а при n=1 удвоения не происходит!)
Victor Kleptsyn
18:17
А если спросить, сколько таких деревьев для n=10, то ответ — 103049 — есть ещё у Плутарха!
Victor Kleptsyn
18:20
И вот соответствующая последовательность —
https://en.wikipedia.org/wiki/Schr%C3%B6der%E2%80%93Hipparchus_number
https://en.wikipedia.org/wiki/Schr%C3%B6der%E2%80%93Hipparchus_number
Victor Kleptsyn
18:25
Тем самым, из всех 10!=3628800 перестановок многочленами реализуется всего лишь
2*103049/10! ~ 5.67%.
Так что "незначительный" запрет на порядки четвёрок, на самом деле, довольно быстро приводит к тому, что реализуется лишь малая доля всех перестановок. Собственно — производящая функция для чисел Шредера-Гиппарха считается явно (что есть несложное упражнение на производящие функции), и имеет конечный радиус сходимости — так что растёт их количество лишь экспоненциальным, а не факториальным, образом:
2*103049/10! ~ 5.67%.
Так что "незначительный" запрет на порядки четвёрок, на самом деле, довольно быстро приводит к тому, что реализуется лишь малая доля всех перестановок. Собственно — производящая функция для чисел Шредера-Гиппарха считается явно (что есть несложное упражнение на производящие функции), и имеет конечный радиус сходимости — так что растёт их количество лишь экспоненциальным, а не факториальным, образом:
Victor Kleptsyn
18:26
(из всё той же статьи Жиса)
Victor Kleptsyn
18:35
In reply to this message
Да, если 5.6% кажется недостаточно малой долей, то для n=20 отношение становится примерно 1.3*10^{-6}. :)
Victor Kleptsyn
18:36
Но — это была лишь отправная точка, как лекции, так и книги. А, наоборот, финальная точка лекции это рассказ про хордовые диаграммы, приходящие из плоских алгебраических кривых.
Victor Kleptsyn
18:43
А именно — пусть на плоскости есть вещественная алгебраическая кривая: множество, заданное уравнением P(x,y)=0. Часто это просто хорошая кривая — скажем, прямая
ax+by+c=0
или окружность
(x-x_0)^2 + (y-y_0)^2 - r^2 =0.
Но иногда на ней бывают особые точки — как начало координат для пары пересекающихся прямых
xy=0
или как "клюв"/"касп"
y^2-x^3=0.
ax+by+c=0
или окружность
(x-x_0)^2 + (y-y_0)^2 - r^2 =0.
Но иногда на ней бывают особые точки — как начало координат для пары пересекающихся прямых
xy=0
или как "клюв"/"касп"
y^2-x^3=0.
Victor Kleptsyn
18:46
Вот пусть начало координат оказалось такой точкой. Точно так же, как оно окажется им для кривой, задаваемой уравнением
(y-P_1(x))*...*(y-P_n(x))=0,
где P_i — многочлены из первой части, обращающиеся в ноль в точке x=0.
(y-P_1(x))*...*(y-P_n(x))=0,
где P_i — многочлены из первой части, обращающиеся в ноль в точке x=0.
Victor Kleptsyn
18:47
Оказывается, что тогда рядом с этой особой точкой кривая разделяется на чётное число входящих в эту точку "ветвей", которые естественным образом разбиваются на пары:
Victor Kleptsyn
18:50
А значит, возникает разбиение на пары на 2n точках, по которым кривая пересекает маленькую окружность вокруг особой точки:
Victor Kleptsyn
18:51
Иными словами — хордовая диаграмма:
Victor Kleptsyn
18:52
И возникает такой же естественный вопрос: а какие хордовые диаграммы реализуются? И сколько их?
Victor Kleptsyn
18:54
(Кстати — тут три запрета это просто поддиаграммы, а вот четвёртый это целое счётное семейство: запрещены "циклы" любой длины n>=5)
Victor Kleptsyn
18:56
На этом я завершаю рассказ про лекцию Жиса — а про его книгу хочу упомянуть ещё три места:
Victor Kleptsyn
18:56
1) Доказательство Гаусса основной теоремы алгебры:
Victor Kleptsyn
19:04
Если на комплексной плоскости задан многочлен P(z), то условие P(z)=0 равносильно паре условий
Re P(z)=0
и
Im P(z)=0.
Re P(z)=0
и
Im P(z)=0.
Victor Kleptsyn
19:05
Давайте я чуть-чуть сэкономлю и скажу, что _пусть_ каждое из этих условий задаёт неособую кривую — а точнее, набор кривых.
Victor Kleptsyn
19:06
Это, конечно, далеко не всегда так — эти кривые могут оказаться особыми, как на этом рисунке (он и предыдущий — из книги Жиса):
Victor Kleptsyn
19:09
Красная кривая тут это Re P(z)=0, а синяя это Im P(z)=0. Особые точки есть на обоих. Иногда бывает так, что особые точки есть только на одной из них (опять же, картинка из книги) —
Victor Kleptsyn
19:10
Но, в любом случае, если чуть-чуть "пошевелить" полином, то они исчезнут. А потом, устремив "шевеление" к нулю и аккуратно проконтролировав происходящее, можно будет найти ноль и у невозмущённого полинома.
(Да, я использую современный анализ вместо того, чтобы аккуратно с особыми точками работать, как раз таки разбираясь с чётностью количества ветвей, но так идея проще рассказывается.)
(Да, я использую современный анализ вместо того, чтобы аккуратно с особыми точками работать, как раз таки разбираясь с чётностью количества ветвей, но так идея проще рассказывается.)
Victor Kleptsyn
19:12
In reply to this message
Так вот — нас интересуют точки пересечения синих и красных кривых. Пусть кривые неособые; посмотрим, что мы видим на большом расстоянии от 0. А видим мы как раз такую картину, как для чистого z^n — в круг большого радиуса R красные и синие ветви входят, чередуясь.
Victor Kleptsyn
19:16
In reply to this message
Раз мы уже предположили, что они неособые, то точки входа по отдельности для красной и для синей кривых разобьются на пары, соединённые неособыми кривыми — как для синей кривой тут.
Victor Kleptsyn
19:18
Но для каждой из синих кривых по каждую сторону от неё чётное число точек входа других синих кривых (раз они не пересекаются) — и потому нечётное число точек входа красной (потому что входы синих и красных чередуются). Значит, каждую синюю кривую хотя бы одна красная пересекает — и вот нам n корней!
Victor Kleptsyn
19:19
(Ещё раз — я, конечно, разобрал только простой "неособый" случай; к нему надо или сводить современным анализом, или аккуратно обрабатывать общий случай, и я ни того, ни другого делать не буду.)
Victor Kleptsyn
19:23
2) Ещё пара кусочков из Ньютона — и до того, как я эти вставки увидел, я не понимал, насколько понятно Ньютон писал.
Victor Kleptsyn
19:27
Единственное, что нам непривычно — это что квадрат переменной обозначается не квадратом, а её произведением на себя. Ну и ещё вертикально-вытянутое написание буквы "s", которую всё хочется принять за "f"
Victor Kleptsyn
19:29
Разложение \sqrt{a^2+x^2} в ряд:
Victor Kleptsyn
М
19:56
Математические байки
И к вопросу о плоских кривых — а почему, собственно, многоугольник Ньютона коэффициентов называют многоугольником Ньютона?
Victor Kleptsyn
20:00
3) Ну и в заключение — "карта странствий", которой книга Жиса открывается:
Victor Kleptsyn
20:02
Ну и на этом рассказ про книгу и лекцию Жиса я хочу завершить.
Victor Kleptsyn
М
20:17
Математические байки
In reply to this message
Последнее на сегодня — Александр Шень меня поправил, что здесь теорема о среднем вытаскивается совсем просто: угол, под которым виден отрезок AB, это разность углов, под которыми наклонены отрезки BX и AX (внешний угол в треугольнике / логарифм отношения, кому как удобнее), а каждый отдельный угол удовлетворяет теореме о среднем просто по симметрии.
Спасибо! :)
Спасибо! :)
Victor Kleptsyn
М
20:36
Математические байки
А завтра в "Математических вечерах ЛШСМ" будет (в 16:00 по Москве) лекция Сергея Горчинского, "Панорама арифметической геометрии".
Victor Kleptsyn
20:37
А у коллег —
Victor Kleptsyn
М
20:37
Математические байки
Г
Геометрия-канал 28.07.2020 22:08:24
В рамках несостоявшегося в этом году очного тура геометрической Олимпиады им. Шарыгина 31 июля 2020 года пройдет два онлайн-мероприятия:
• С 19:00 до 20:00 лекция Г.Ю.Паниной «Задача о ворах, укравших ожерелье».
• С 20:00 вечер поэзии, организованный Г.Б.Филипповским и В.Ю.Протасовым — читаем любимые стихи и общаемся.
Оба мероприятия проходят в zoom
(id: 712 442 4665; пароль: две единицы и следующие четыре числа Фибоначчи).
• С 19:00 до 20:00 лекция Г.Ю.Паниной «Задача о ворах, укравших ожерелье».
• С 20:00 вечер поэзии, организованный Г.Б.Филипповским и В.Ю.Протасовым — читаем любимые стихи и общаемся.
Оба мероприятия проходят в zoom
(id: 712 442 4665; пароль: две единицы и следующие четыре числа Фибоначчи).
Victor Kleptsyn
31 July 2020
М
16:06
Математические байки
Лекция Горчинского начинается:
Victor Kleptsyn
1 August 2020
М
15:58
Математические байки
In reply to this message
Ещё от А. Шеня, первая — ещё студенческая — заметка В. А. Успенского: http://mi.mathnet.ru/umn8612
Пара скриншотов оттуда:
Пара скриншотов оттуда:
Victor Kleptsyn
16:00
А через пару минут начинается заключительная лекция "Математических вечеров ЛШСМ"
Victor Kleptsyn
М
16:02
Математические байки
Н
Непрерывное математическое образование 01.08.2020 15:00:09
Математические вечера ЛШСМ завершаются. Сегодня в 16 часов — последняя лекция, А.П.Веселов и В.Ю.Овсиенко будут рассказывать старое и новое о цепных дробях
«Хорошо известно, что обычные цепные дроби полезны для рациональных приближений действительных чисел, и что периодические цепные дроби — это в точности квадратичные иррациональности. Оказывается, что аналоги цепных дробей над кольцом полиномов от одной переменной полезны для описания эллиптических интегралов, берущихся в элементарных функциях. Об этих замечательных результатах Абеля и Чебышева будет рассказано в первой части лекции.
Во второй части будет рассказано о новой версии подобных цепных дробей, возникшей недавно в связи с комбинаторикой и кластерными алгебрами. Эта новая версия оказалась связанной также с теорией узлов и легла в основу понятия “квантовых” или “q-деформированных” чисел.»
«Хорошо известно, что обычные цепные дроби полезны для рациональных приближений действительных чисел, и что периодические цепные дроби — это в точности квадратичные иррациональности. Оказывается, что аналоги цепных дробей над кольцом полиномов от одной переменной полезны для описания эллиптических интегралов, берущихся в элементарных функциях. Об этих замечательных результатах Абеля и Чебышева будет рассказано в первой части лекции.
Во второй части будет рассказано о новой версии подобных цепных дробей, возникшей недавно в связи с комбинаторикой и кластерными алгебрами. Эта новая версия оказалась связанной также с теорией узлов и легла в основу понятия “квантовых” или “q-деформированных” чисел.»
Victor Kleptsyn
М
16:51
Математические байки
In reply to this message
Алаверды к появившемуся на доске уравнению Пелля —
В. О. Бугаенко, "Уравнения Пелля":
https://www.mccme.ru/free-books/mmmf-lectures/book.13.pdf
В. О. Бугаенко, "Уравнения Пелля":
https://www.mccme.ru/free-books/mmmf-lectures/book.13.pdf
Victor Kleptsyn
16:52
Ещё "слайды" из сегодняшнего рассказа —
Victor Kleptsyn
16:53
И ещё —
Victor Kleptsyn
8 August 2020
М
12:25
Математические байки
Н
Непрерывное математическое образование 08.08.2020 12:22:16
80 лет назад родился Николай Борисович Васильев (08.08.1940–28.05.1998)
http://mi.mathnet.ru/mp35
http://kvant.mccme.ru/au/vasilev_n.htm
http://mi.mathnet.ru/mp35
http://kvant.mccme.ru/au/vasilev_n.htm
Victor Kleptsyn
12:48
Можно ли разрезать треугольник вершиной вверх на конечное число частей (прямолинейными разрезами), сдвинуть каждую из них, не поворачивая, и получить треугольник вершиной вниз?
Victor Kleptsyn
12:53
In reply to this message
Этот вопрос задавал Сэмюэль Лойд — автор множества головоломок; а с картинки выше начинается вот эта статья — https://images.math.cnrs.fr/La-mesure-des-figures-du-plan.html .
Собственно, Images de Maths я очень люблю, и там есть ещё много интересного — например, рассказ о "кубическом" футбольном мяче, http://images.math.cnrs.fr/Le-Brazuca-le-ballon-cubique-de-la-Coupe-du-monde , заслуживает отдельного поста.
Собственно, Images de Maths я очень люблю, и там есть ещё много интересного — например, рассказ о "кубическом" футбольном мяче, http://images.math.cnrs.fr/Le-Brazuca-le-ballon-cubique-de-la-Coupe-du-monde , заслуживает отдельного поста.
Victor Kleptsyn
13:02
Кстати — без запрета на повороты частей ответ на вопрос, когда из одной фигуры "ножницами" можно сделать другую, даёт теорема Бойяи--Гервина. А именно — два многоугольника равносоставлены тогда и только тогда, когда у них совпадают площади. Часть "только тогда" очевидна — а вот для "тогда" нужно поработать; правда, доказательство получается вполне обозримым.
Victor Kleptsyn
М
13:56
Математические байки
Первый раз я его, кажется, услышал на лекции А. А. Гайфуллина два года назад на ЛШСМ — http://www.mathnet.ru/present21265 ; удивительно поздно, с учётом того, что рассуждение абсолютно школьное — но как-то раньше я факт знал, а доказательство посмотреть руки не доходили.
Собственно, понятно, что равносоставленность это отношение транзитивное (если A~B и B~C, то A~C: из аналогии с ножницами это очень хорошо видно).
Поэтому можно выбрать единицу длины и доказывать, что любая фигура равносоставлена прямоугольнику размера 1xS.
А поскольку любой многоугольник можно разрезать на треугольники — то достаточно это доказать для всех треугольников. Наконец, треугольник просто превратить в параллелограмм:
Собственно, понятно, что равносоставленность это отношение транзитивное (если A~B и B~C, то A~C: из аналогии с ножницами это очень хорошо видно).
Поэтому можно выбрать единицу длины и доказывать, что любая фигура равносоставлена прямоугольнику размера 1xS.
А поскольку любой многоугольник можно разрезать на треугольники — то достаточно это доказать для всех треугольников. Наконец, треугольник просто превратить в параллелограмм:
Victor Kleptsyn
14:07
Следующее упражнение, что два параллелограмма с равной площадью и общим основанием равносоставлены. Пока они не сильно наклонены, можно обойтись вообще одним переставляемым треугольником:
Victor Kleptsyn
14:12
А в общем случае можно либо нарезать на тонкие горизонтальные слои, или (что мне нравится больше) наклеить параллелограммы на цилиндр так, чтобы общее основание превратилось в окружность-параллель этого цилиндра. И тогда наклейка будет "в один слой", а граница одного из параллелограммов покажет, где нужно разрезать другой.
Victor Kleptsyn
14:13
Кстати, можно я вспомню задачу про верблюда?
Victor Kleptsyn
М
14:14
Математические байки
Н
Непрерывное математическое образование 09.02.2020 17:00:36
самый лучший способ увидеть решение — паркет из верблюдов
Victor Kleptsyn
М
14:17
Математические байки
Остаётся совсем чуть-чуть (и это, мне кажется, самый изящный шаг доказательства): если начать "перекашивать" параллелограмм — его вторая сторона будет расти. Значит, в какой-то момент она станет целой — равной какому-то k. После чего можно взять за основание уже её — и превратить параллелограмм в прямоугольник k x L, а его уже, разрезав k как 1+1+...+1 — в прямоугольник 1 x S.
Victor Kleptsyn
14:22
Всё! Треугольник площади S равносоставлен прямоугольнику 1 x S — а значит, то же правда и про любой многоугольник. Вот так теорема Бойяи--Гервина и доказывается.
Victor Kleptsyn
14:24
Давайте я добавлю пару ссылок. Другое доказательство есть в "миниатюрах" Математических этюдов:
https://www.etudes.ru/ru/sketches/hilbert-third-problem/
(а почему "третья проблема Гильберта, я сейчас скажу пару слов").
https://www.etudes.ru/ru/sketches/hilbert-third-problem/
(а почему "третья проблема Гильберта, я сейчас скажу пару слов").
Victor Kleptsyn
14:25
Там рассуждение проходит через квадраты — и через (заодно) доказывающее теорему Пифагора объединение двух квадратов в один:
Victor Kleptsyn
М
14:42
Математические байки
Это же рассуждение в калейдоскопе "Кванта" (а также несколько явных красивых примеров равносоставленности) — http://kvant.ras.ru/pdf/2016/2016-02.pdf
(см. с. 34--35 PDF-файла).
(см. с. 34--35 PDF-файла).
Victor Kleptsyn
М
15:36
Математические байки
Н
Непрерывное математическое образование 29.10.2019 11:15:18
про теорему Бойяи–Гервина — а также про теорему Дена (показывающую, что, в отличие от многоугольников, равновеликие многогранники не всегда равносоставленны) — можно еще прочитать в брошюре В.Г.Болтянского, http://mathedu.ru/lib/books/boltyanskiy_ravnovelikie_i_ravnosostavlennye_figury_1956/#38 (и еще про инвариант Дена объясняется в одной из глав «Математического дивертисмента» Табачникова и Фукса)
на этом история не заканчивается: в 1965 году Сидле (Sydler) доказал обратное утверждение: если у многогранников равны и объемы, и инварианты Дена, то они равносоставленны (и эта история оказывается связанной с гомологиями групп неожиданно) — про все это рассказывал на ЛШСМ-2018 А.А.Гайфуллин, можно посмотреть видеозаписи:
http://www.mathnet.ru/present21265
http://www.mathnet.ru/present21725
http://www.mathnet.ru/present21726
http://www.mathnet.ru/present21727
http://www.mathnet.ru/present21728
видеолекции выше доступны и для старшеклассников, а люди с чуть более серьезной подготовкой могут также посмотреть обзор L.Hesselholt'а
https://www.math.nagoya-u.ac.jp/~larsh/teaching/F2011_PM/lecture.pdf
на этом история не заканчивается: в 1965 году Сидле (Sydler) доказал обратное утверждение: если у многогранников равны и объемы, и инварианты Дена, то они равносоставленны (и эта история оказывается связанной с гомологиями групп неожиданно) — про все это рассказывал на ЛШСМ-2018 А.А.Гайфуллин, можно посмотреть видеозаписи:
http://www.mathnet.ru/present21265
http://www.mathnet.ru/present21725
http://www.mathnet.ru/present21726
http://www.mathnet.ru/present21727
http://www.mathnet.ru/present21728
видеолекции выше доступны и для старшеклассников, а люди с чуть более серьезной подготовкой могут также посмотреть обзор L.Hesselholt'а
https://www.math.nagoya-u.ac.jp/~larsh/teaching/F2011_PM/lecture.pdf
Victor Kleptsyn
М
15:37
Математические байки
А если посмотреть на с. 15 Болтянского —
https://www.mathedu.ru/text/boltyanskiy_ravnovelikie_i_ravnosostavlennye_figury_1956/p15/ — то оказывается, что хватает параллельных переносов и центральных симметрий:
https://www.mathedu.ru/text/boltyanskiy_ravnovelikie_i_ravnosostavlennye_figury_1956/p15/ — то оказывается, что хватает параллельных переносов и центральных симметрий:
Victor Kleptsyn
М
15:56
Математические байки
В размерности 3 всё не так, как на плоскости. Вопрос о равносоставленности многогранников был третьей проблемой Гильберта, и отрицательный ответ (например, неравносоставленность куба и правильного тетраэдра одинаковых объёмов) следует из наличия дополнительного инварианта, инварианта Дэна.
Интересно, что этому посвящён один из текстов Mathesis-а — https://www.mathesis.ru/book/kagan2/ :
Интересно, что этому посвящён один из текстов Mathesis-а — https://www.mathesis.ru/book/kagan2/ :
Victor Kleptsyn
15:58
Как знакомо —
Victor Kleptsyn
16 August 2020
М
11:16
Математические байки
In reply to this message
Продолжим?
Давайте вернёмся к исходному вопросу про параллельные переносы. Ответ на него отрицательный — и как обычно при доказательстве не-существования, нужен инвариант.
И тут он очень простой: суммарная длина горизонтальных отрезков, являющихся "нижними" сторонами фигуры, минус суммарная длина горизонтальных отрезков, являющихся "верхними" сторонами.
Давайте вернёмся к исходному вопросу про параллельные переносы. Ответ на него отрицательный — и как обычно при доказательстве не-существования, нужен инвариант.
И тут он очень простой: суммарная длина горизонтальных отрезков, являющихся "нижними" сторонами фигуры, минус суммарная длина горизонтальных отрезков, являющихся "верхними" сторонами.
Victor Kleptsyn
11:17
Понятно, что это инвариант (при проведении разрезов обе длины меняются одинаково, так что их разность не меняется) — и столь же очевидно, что он наши два треугольника различает.
Конечно же, такую же разность можно посчитать для любого другого направления, не обязательно для горизонтального. Так что инвариантом будет аж целая функция от направления (правда, отличная от нуля лишь в конечном числе точек).
Конечно же, такую же разность можно посчитать для любого другого направления, не обязательно для горизонтального. Так что инвариантом будет аж целая функция от направления (правда, отличная от нуля лишь в конечном числе точек).
Victor Kleptsyn
11:19
Собственно, коллеги про это уже написали:
Victor Kleptsyn
М
11:19
Математические байки
Н
Непрерывное математическое образование 12.08.2020 12:04:39
https://www.turgor.ru/lktg/2007/1/1-1ru.pdf
на тему разрезания многоугольников и многогранников — напомним еще такой материал с ЛКТГ-2007 (М.Прасолов, М.Скопенков, Б.Френкин)
в т.ч. из текста можно узнать, как решать задачу выше про два треугольника
конкретно про это, впрочем, и здесь написать не долго: величина (суммарная длина горизонтальных сторон, к которым многоугольник примыкает снизу) – (<…> сверху) является инвариантом
на тему разрезания многоугольников и многогранников — напомним еще такой материал с ЛКТГ-2007 (М.Прасолов, М.Скопенков, Б.Френкин)
в т.ч. из текста можно узнать, как решать задачу выше про два треугольника
конкретно про это, впрочем, и здесь написать не долго: величина (суммарная длина горизонтальных сторон, к которым многоугольник примыкает снизу) – (<…> сверху) является инвариантом
Victor Kleptsyn
М
11:20
Математические байки
А что, если все такие разности — и площадь, без неё никуда — у двух фигур одинаковы?
Victor Kleptsyn
11:21
Например, у квадрата эти разности нулевые. А можно ли "повернуть" квадрат, если из разрешённых операций есть только разрезание и параллельный перенос?
Victor Kleptsyn
11:22
(Изображение из первой части всё той же статьи в Images de Maths, https://images.math.cnrs.fr/Un-triangle-et-une-enigme.html )
Victor Kleptsyn
11:24
Так вот — оказывается, повернуть квадрат можно. И это делается с помощью дважды применённого "пифагорского" разрезания:
Victor Kleptsyn
11:24
(картинка оттуда же)
Victor Kleptsyn
11:28
In reply to this message
Более того, теорема Хадвигера-Глюра утверждает, что инвариант действительно полный: из уже процитированного текста с ЛКТГ-2007 —
Victor Kleptsyn
М
11:45
Математические байки
А вот исходная статья Хадвигера-Глюра, где эта теорема появляется:
https://gdz.sub.uni-goettingen.de/id/PPN378850199_0006?tify={%22pages%22:[101],%22view%22:%22export%22}
Собственно, очень интересно её полистать (особенно, когда знаешь, что там должно быть написано — удивительное ощущение, когда язык перестаёт быть препятствием, хоть статья и по-немецки).
Вот тут вводится инвариант —
https://gdz.sub.uni-goettingen.de/id/PPN378850199_0006?tify={%22pages%22:[101],%22view%22:%22export%22}
Собственно, очень интересно её полистать (особенно, когда знаешь, что там должно быть написано — удивительное ощущение, когда язык перестаёт быть препятствием, хоть статья и по-немецки).
Вот тут вводится инвариант —
Victor Kleptsyn
11:46
А вот теорема о том, что это критерий:
Victor Kleptsyn
11:47
Аккуратные картинки с разрезаниями и перестановками —
Victor Kleptsyn
М
12:16
Математические байки
А что будет в пространстве, — для начала, если можно только параллельно переносить части? Каким будет полный инвариант?
Конечно, будет сохраняться объём. И точно так же, как и раньше, можно взять горизонтальные грани, и вычесть из полной площади "нижних" горизонтальных граней полную площадь "верхних" горизонтальных граней. И точно так же можно сделать вообще для любой плоскости — посчитать с разными знаками площади параллельных ей граней, в зависимости от того, в какую сторону смотрит внешняя нормаль.
А всё ли это?
Конечно, будет сохраняться объём. И точно так же, как и раньше, можно взять горизонтальные грани, и вычесть из полной площади "нижних" горизонтальных граней полную площадь "верхних" горизонтальных граней. И точно так же можно сделать вообще для любой плоскости — посчитать с разными знаками площади параллельных ей граней, в зависимости от того, в какую сторону смотрит внешняя нормаль.
А всё ли это?
Victor Kleptsyn
М
12:35
Математические байки
На самом деле — нет, не всё. Потому что у каждой грани есть не только площадь — но и плоский инвариант Хадвигера! Поэтому для каждой плоскости и для каждого направления в этой плоскости у нас будет инвариантная величина — знакопеременная сумма по граням, параллельным плоскости, от тоже знакопеременной суммы длин параллельных этому направлению рёбер.
Victor Kleptsyn
М
13:04
Математические байки
А вот теперь уже точно всё — такой набор это уже полный инвариант. А вот фотография доски с заключительного занятия курса А. Гайфуллина на ЛШСМ-2018, http://www.mathnet.ru/php/presentation.phtml?presentid=21728&option_lang=rus (70-я минута):
Victor Kleptsyn
М
14:42
Математические байки
In reply to this message
Да, тот курс был совершенно замечательный; и вот один из прекрасных результатов оттуда, который я не побоюсь назвать его жемчужиной.
Есть такие интересные объекты — изгибаемые многогранники. Представим себе, что у многогранника грани жёсткие, "сделаны из дерева", но на рёбрах сходятся под произвольным углом (скреплены клейкой лентой для маленькой модели — или дверными петлями для большой). Если сделать такой куб — он будет жёстким. А некоторые многогранники — нет, их оказывается возможным непрерывно изгибать!
Есть такие интересные объекты — изгибаемые многогранники. Представим себе, что у многогранника грани жёсткие, "сделаны из дерева", но на рёбрах сходятся под произвольным углом (скреплены клейкой лентой для маленькой модели — или дверными петлями для большой). Если сделать такой куб — он будет жёстким. А некоторые многогранники — нет, их оказывается возможным непрерывно изгибать!
Victor Kleptsyn
14:43
Оказывается, кузнечные меха из изгибаемого многогранника делать бессмысленно: в процессе изгибания его объём остаётся постоянным. Это следует из теоремы Сабитова; я тут процитирую брошюру Н. П. Долбилина, "Жемчужины теории многогранников" (https://www.mccme.ru/mmmf-lectures/books/books/book.5.pdf ) :
Victor Kleptsyn
14:44
In reply to this message
Так вот, оказывается — и это совместный результат А.А.Гайфуллина и Л.С. Игнащенко 2017 (!) года — что изгибаемый многогранник не просто сохраняет свой объём в процессе изгибания, а любые его два положения в процессе изгибания равносоставлены друг другу: можно его разрезать на конечное число частей, их переставить-повернуть, объединить, и получить другое положение.
Victor Kleptsyn
14:45
Более того — некоторое время считалось, что к этому утверждению построен контрпример; я процитирую тут аннотацию к их статье, http://mi.mathnet.ru/rus/tm/v302/p143 :
Victor Kleptsyn
14:45
При n=3 и n=4 отсюда следует, что всякий изгибаемый многогранник остается равносоставленным с самим собой в процессе изгибания, что доказывает сильную гипотезу о кузнечных мехах, выдвинутую Р. Коннелли в 1979 г. Считалось, что в 2009 г. к этой гипотезе был построен контрпример В.А. Александровым и Р. Коннелли. Однако в настоящей работе показано, что их результат содержит неустранимую ошибку.
Victor Kleptsyn
14:51
Вещь совершенно замечательная — с очень красивым рассуждением, использующим комплексное продолжение, логарифмы, формулу Шлефли и теорему Лиувилля.
А вот ссылка на видеозапись именно той лекции, где это рассказывается — http://www.mathnet.ru/php/presentation.phtml?presentid=21727&option_lang=rus (и ещё один рассказ есть тут — http://www.mathnet.ru/present19144 ).
А вот ссылка на видеозапись именно той лекции, где это рассказывается — http://www.mathnet.ru/php/presentation.phtml?presentid=21727&option_lang=rus (и ещё один рассказ есть тут — http://www.mathnet.ru/present19144 ).
Victor Kleptsyn
14:56
In reply to this message
Слева то, что нужно для равносоставленности: постоянство инварианта Дэна. Справа — теорема Лиувилля: ограниченная целая функция постоянна.
Ну и на этой "сцепке" (из которой становится понятно, зачем нужно комплексное продолжение, и как хотя бы в принципе доказательство может работать) я эту байку на сегодня завершу.
Ну и на этой "сцепке" (из которой становится понятно, зачем нужно комплексное продолжение, и как хотя бы в принципе доказательство может работать) я эту байку на сегодня завершу.
Victor Kleptsyn
14:58
In reply to this message
Да, а ещё коллеги напомнили, что у канала вчера был день рождения!
Victor Kleptsyn
19 August 2020
М
17:06
Математические байки
Н
Непрерывное математическое образование 19.08.2020 17:05:34
https://youtu.be/mH0oCDa74tE
Вышло новое видео 3blue1brown — от обсуждения того, что такое группы и зачем они нужны, до Монстра (простой группы порядка 808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000)
Бонус для желающих подробностей: http://www.ams.org/notices/200209/what-is.pdf — короткий текст Борчердса про Монстра (из серии «What is…»)
Вышло новое видео 3blue1brown — от обсуждения того, что такое группы и зачем они нужны, до Монстра (простой группы порядка 808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000)
Бонус для желающих подробностей: http://www.ams.org/notices/200209/what-is.pdf — короткий текст Борчердса про Монстра (из серии «What is…»)
Victor Kleptsyn
20 August 2020
М
10:45
Математические байки
In reply to this message
На странице https://www.mccme.ru/dubna/lect2020/ выложены ссылки на видеозаписи всех лекций — и слайды/запись доски от некоторых из них.
Ещё они есть одним плейлистом —
https://www.youtube.com/watch?v=xRRNCuxLEyQ&list=PLp9ABVh6_x4ET5so529u3C129XqkY8Gn_ ; и они же на mathnet-е — http://www.mathnet.ru/conf1828 .
Ещё они есть одним плейлистом —
https://www.youtube.com/watch?v=xRRNCuxLEyQ&list=PLp9ABVh6_x4ET5so529u3C129XqkY8Gn_ ; и они же на mathnet-е — http://www.mathnet.ru/conf1828 .
Victor Kleptsyn
21 August 2020
М
19:31
Математические байки
In reply to this message
Давайте я скажу ещё пару слов про исходную задачу — про то, что треугольники вершиной вверх и вниз разрезаниями и параллельными переносами друг в друга превратить нельзя. А именно, интересно, что в "Images de Maths" эту невозможность рассказывают по-другому. И мне тут потребуется экскурс, казалось бы, совсем в сторону.
Victor Kleptsyn
19:32
Если у нас (на плоскости, или в R^n) есть два множества, A и B, то можно определить их сумму Минковского: просто множество всевозможных сумм x+y:
A+B = {x+y | x\in A, y\in B}
A+B = {x+y | x\in A, y\in B}
Victor Kleptsyn
19:32
Правда, при таком определении расположение этой суммы будет зависеть от того, где находится начало координат, так что давайте сразу рассматривать множества с точностью до параллельного переноса.
Victor Kleptsyn
19:34
Если вместо суммы брать полусумму — то получится множество середин отрезков, соединяющих точки этих множеств. И я тут хочу вспомнить статью Н. Б. Васильева "Сложение фигур" в "Кванте" — http://kvant.mccme.ru/1976/04/slozhenie_figur.htm .
Victor Kleptsyn
19:34
Кстати — хорошая задача оттуда: как выглядит ГМТ середин отрезков, соединяющих две точки на полуокружности?
Victor Kleptsyn
19:38
In reply to this message
Иллюстрация оттуда же — показывающая много разных сумм Минковского:
Victor Kleptsyn
19:40
Если множества A и B выпуклые, то и их сумма A+B выпуклая. (Собственно, с этой задачи статья Н. Б. Васильева и начинается.)
А сумма множества A с кругом/с шаром радиуса ε это ε -окрестность A.
А сумма множества A с кругом/с шаром радиуса ε это ε -окрестность A.
Victor Kleptsyn
19:41
А как устроена площадь ε-окрестности выпуклой фигуры на плоскости?
Victor Kleptsyn
19:43
Легко понять, что при небольших ε она возрастает примерно на (периметр фигуры)*ε. А в старшей размерности — объём фигуры увеличивается в первом порядке на ε*(её площадь поверхности).
Victor Kleptsyn
19:45
Утверждение, которое меня в своё время удивило: площадь ε-окрестности A_ε выпуклой фигуры A на плоскости — многочлен от ε:
S(A_ε) = S(A)+ε*L(A)+πε^2,
где L(A) — периметр A.
S(A_ε) = S(A)+ε*L(A)+πε^2,
где L(A) — периметр A.
Victor Kleptsyn
19:45
Доказательство для случая многоугольника:
Victor Kleptsyn
19:46
ε-окрестность разбивается на сам многоугольник, прямоугольники, построенные на его сторонах, и сектора в вершинах, собирающиеся в точности в круг радиуса ε.
Victor Kleptsyn
19:47
Эта иллюстрация для случая треугольника — но для случая любого выпуклого многоугольника будет то же самое. Кстати, собирающиеся сектора это то же самое рассуждение, что сумма внешних углов выпуклого многоугольника равна 2π:
Victor Kleptsyn
19:48
(Изображение из Мат. этюдов — https://etudes.ru/ru/models/exterior-angles-sum/ )
Victor Kleptsyn
19:50
In reply to this message
Правда, тут внешние углы, а наши сектора это угол между перпендикулярами вовне к сторонам, но одно от другого отличается поворотом на 90 градусов.
Victor Kleptsyn
19:51
Так что — площадь ε-окрестности выпуклой фигуры это в точности многочлен второй степени от ε!
Victor Kleptsyn
19:56
В пространстве будет то же самое — только многочлен от радиуса окрестности уже будет третьей степени; понятно, что свободным членом будет объём, линейным ε*площадь поверхности, кубическим — объём того шара радиуса ε, в который соберутся торчащие в вершинах кусочки.
Victor Kleptsyn
19:58
А вот с квадратичным членом интереснее — коэффициентом при ε^2 будет сумма по рёбрам
"(длина ребра)"*"(внешний двугранный угол)"; очень напоминает инвариант Дена, но я не знаю дороги к нему отсюда.
"(длина ребра)"*"(внешний двугранный угол)"; очень напоминает инвариант Дена, но я не знаю дороги к нему отсюда.
Victor Kleptsyn
19:59
Да, ещё на этом множестве выпуклых фигур с точностью до параллельного переноса есть естественная операция умножения на положительное число — просто гомотетия. И легко видеть, что она хорошо со сложением по Минковскому согласована:
aA+bA=(a+b)A.
aA+bA=(a+b)A.
Victor Kleptsyn
20:05
А что можно сказать о площади "линейной комбинации" aA+bB двух выпуклых множеств A и B с положительными коэффициентами a,b>0? Оказывается, это однородный многочлен степени 2:
S(aA+bB)=a^2*S(A)+b^2*S(B)+2ab*S(A,B),
где S(A,B) — некоторая величина, которую мы назовём смешанной площадью фигур A и B.
Немного напоминает, как по квадратичной форме восстанавливается билинейная, правда?
S(aA+bB)=a^2*S(A)+b^2*S(B)+2ab*S(A,B),
где S(A,B) — некоторая величина, которую мы назовём смешанной площадью фигур A и B.
Немного напоминает, как по квадратичной форме восстанавливается билинейная, правда?
Victor Kleptsyn
20:07
In reply to this message
А вообще множество выпуклых тел уже почти является линейным пространством — только вычитать нельзя. Ну если нельзя, но очень хочется, то можно: давайте его превратим в линейное пространство, добавив "формальные разности" двух множеств. А именно, рассмотрим все формальные "разности" A-B выпуклых множеств, и отфакторизовав по отношению эквивалентности: положим
A-B=C-D,
если
A+D=B+C
(немного напоминает определение поля частных, правда? и кстати, проверять нужно тоже похожие вещи, хоть я это сейчас и под ковёр заметаю)
A-B=C-D,
если
A+D=B+C
(немного напоминает определение поля частных, правда? и кстати, проверять нужно тоже похожие вещи, хоть я это сейчас и под ковёр заметаю)
Victor Kleptsyn
20:08
В таком линейном пространстве настоящие выпуклые многогранники/тела будут его частью — выпуклым конусом.
Victor Kleptsyn
20:14
Так вот, и давайте я тут сошлюсь на записки одной из лекций курса Владлена Тиморина (на который я в своё время ходил — и с тех пор эти вещи и помню!) — https://users.mccme.ru/valya/lect3.pdf — оказывается, что функция объёма выпуклых тел в R^n это однородный многочлен степени n.
Или, более формально, становится многочленом в ограничении на любое конечномерное подпространство в пространстве всех выпуклых тел — если мы будем рассматривать
Vol(t_1 A_1+...+t_k A_k), где t_1,..,t_k>0
то получим однородный многочлен от t_1,...,t_k.
Или, более формально, становится многочленом в ограничении на любое конечномерное подпространство в пространстве всех выпуклых тел — если мы будем рассматривать
Vol(t_1 A_1+...+t_k A_k), где t_1,..,t_k>0
то получим однородный многочлен от t_1,...,t_k.
Victor Kleptsyn
20:16
И соответственно, объёму Vol(A) как многочлену степени n можно сопоставить функцию
Vol(A_1,...,A_n),
симметричную и линейную (в смысле сложения по Минковскому!) по каждому аргументу, которая превращается в обычный объём, когда вместо всех аргументов подставляется одно и то же A.
Vol(A_1,...,A_n),
симметричную и линейную (в смысле сложения по Минковскому!) по каждому аргументу, которая превращается в обычный объём, когда вместо всех аргументов подставляется одно и то же A.
Victor Kleptsyn
20:16
Эта функция называется смешанным объёмом.
Victor Kleptsyn
20:19
In reply to this message
Так вот — давайте я теперь вернусь к исходной задаче. Пусть T — треугольник вершиной вверх, T' — треугольник вершиной вниз. Нам нужно придумать инвариант от "разрезания+ параллельного переноса", который их различит. Можно считать, что мы всегда режем на выпуклые части — если вдруг какая-то часть это невыпуклый многоугольник, то доразрежем его хоть на треугольники, а потом всё вместе перенесём.
Victor Kleptsyn
20:21
Рассмотрим функцию —
F(A) := S(A+T) - S(A+T').
Утверждение:
а) это инвариант: если мы разрезаем фигуру на выпуклые части, то значение на фигуре равно сумме значений на частях.
б) он различает T и T'.
F(A) := S(A+T) - S(A+T').
Утверждение:
а) это инвариант: если мы разрезаем фигуру на выпуклые части, то значение на фигуре равно сумме значений на частях.
б) он различает T и T'.
Victor Kleptsyn
20:22
Второе проверить проще: для A=T
S(T+T)=S(2T)=4S(T),
S(T+T')=S(шестиугольника)=6S(T),
F(T)=-2S(T);
F(T')=-F(T)=2S(T).
S(T+T)=S(2T)=4S(T),
S(T+T')=S(шестиугольника)=6S(T),
F(T)=-2S(T);
F(T')=-F(T)=2S(T).
Victor Kleptsyn
20:27
А при проверке первого удобно воспользоваться как раз знанием о том, как именно устроены площади сумм Минковского:
F(A)=(S(A)+S(T)+2S(A,T)) - (S(A)+S(T')+2S(A,T')) =
S(A,T)-S(A,T'),
поэтому этот инвариант — это разница двух смешанных площадей.
F(A)=(S(A)+S(T)+2S(A,T)) - (S(A)+S(T')+2S(A,T')) =
S(A,T)-S(A,T'),
поэтому этот инвариант — это разница двух смешанных площадей.
Victor Kleptsyn
20:30
И если поверить в то, что за смешанные площади "отвечают" стороны, и добавить к этому, что при проведении разреза появляются как раз стороны противоположно направленные стороны с двух берегов разреза — то не очень сложно увидеть, что вклад верхней стороны в S(A,T) сократится с вкладом нижней в S(A,T').
Victor Kleptsyn
20:37
Вот мы и получили неравносоставленность треугольников с вершинами вверх и вниз — и более того, добыли инвариант такой равносоставленности.
Ну и такой же инвариант можно построить и для любой другой фигуры T, лишь бы T' было её центрально-симметричным образом. А если посмотреть, что же именно мы при этом считаем — то будут получаться какие-то интегральные выражения от того инварианта Хадвигера, который мы построили раньше. И если мы его не придумали тогда — то его можно было бы придумать, идя от этих инвариантов, задавшись вопросом "а что же мы интегрируем".
Ну и такой же инвариант можно построить и для любой другой фигуры T, лишь бы T' было её центрально-симметричным образом. А если посмотреть, что же именно мы при этом считаем — то будут получаться какие-то интегральные выражения от того инварианта Хадвигера, который мы построили раньше. И если мы его не придумали тогда — то его можно было бы придумать, идя от этих инвариантов, задавшись вопросом "а что же мы интегрируем".
Victor Kleptsyn
20:39
In reply to this message
Да, давайте я скопирую сюда иллюстрацию из всё тех же записок курса Владлена Тиморина, https://users.mccme.ru/valya/lect3.pdf — и формулировку теоремы Штейнера-Минковского:
Victor Kleptsyn
20:41
In reply to this message
Видны и "секторные" окрестности, возникающие на рёбрах, и "шапочки" окрестностей в вершинах.
Victor Kleptsyn
20:43
А ещё — сложение по Минковскому можно объявить не сложением, а... умножением. И об этом рассказывала в ЛШСМ-2013 Гаянэ Панина, см. https://www.mccme.ru/dubna/2013/courses/panina.htm + http://www.mathnet.ru/php/presentation.phtml?option_lang=rus&presentid=7277
Victor Kleptsyn
20:44
Скриншот из видеозаписи первого занятия —
Victor Kleptsyn
20:44
И на этом я на сегодня прекращаю дозволенные речи.
Victor Kleptsyn
23 August 2020
М
13:04
Математические байки
In reply to this message
Продолжил оглавление — с того места, докуда доходило оглавление в архиве. Получилось немало:
Victor Kleptsyn
13:04
Ещё немного асимптотической комбинаторики: Random Sorting Networks — https://t.me/mathtabletalks/898
Алиса и Боб: кто скорее разорился раньше? https://t.me/mathtabletalks/931
Слова Фибоначчи, квазикристаллы и фрактал Рози — https://t.me/mathtabletalks/948
Записки из Warwick-а
https://t.me/mathtabletalks/1053
Два взгляда на теорему о высотах в сферической геометрии (и на плоскости Лобачевского) — https://t.me/mathtabletalks/1080
Пара слов с Матпраздника — https://t.me/mathtabletalks/1123
... и рассказ о числах Мерсенна: как их проверяют на простоту? https://t.me/mathtabletalks/1129
Бильярды в треугольниках и не только — https://t.me/mathtabletalks/1178
Задача о пересылке бриллианта и применение эллиптических кривых в криптографии для защиты... https://t.me/mathtabletalks/1198
... и для нападения (алгоритм факторизации Ленстры) — https://t.me/mathtabletalks/1244
Игла Бюффона: как обойтись совсем без интегрирования — https://t.me/mathtabletalks/1264
Лекция Ингрид Добеши на ICM-2018: холсты из одного рулона (и кто бы мог подумать, что это можно будет проверить) — https://t.me/mathtabletalks/1279
Доказательство Ламберта иррациональности π: цепная дробь для тангенса (!) — https://t.me/mathtabletalks/1307
(и цепные дроби вообще, и небольшое упоминание фризов https://t.me/mathtabletalks/1402 )
... и последовательности Фарея https://t.me/mathtabletalks/1464
Премия Абеля — работы Фюрстенберга https://t.me/mathtabletalks/1514
Два слова о числах Каталана — https://t.me/mathtabletalks/1586
Абелевский сезон, продолжение — работы Маргулиса: https://t.me/mathtabletalks/1638
Факторизация: как работает метод квадратичного решета — начало (метод Диксона) https://t.me/mathtabletalks/1691 + окончание https://t.me/mathtabletalks/1716
Абелевский сезон-2, продолжение о работах Маргулиса: https://t.me/mathtabletalks/1727
Вспоминая Конвея:
лексикографические коды https://t.me/mathtabletalks/1750
несколько фотографий https://t.me/mathtabletalks/1791
программируя на FRACTRAN-е https://t.me/mathtabletalks/1797
статья о разных доказательствах иррациональности корня из двух — https://t.me/mathtabletalks/1803
(и отступление к доказательству рождественской теореме Ферма https://t.me/mathtabletalks/1822 )
статья "A Headache Causing Problem" https://t.me/mathtabletalks/1849
Катящиеся окружности и гипоциклоиды в них — https://t.me/mathtabletalks/1889
Рассказ о комплексной динамике, начало (когда множество Жюлиа связно?) —
https://t.me/mathtabletalks/1919
Уходя в далёкое прошлое — https://t.me/mathtabletalks/1943
Упаковки шаров: начало —https://t.me/mathtabletalks/2003
Кватернионы, вращения и правильные многогранники — https://t.me/mathtabletalks/2054
Упаковки шаров: продолжение — решётка E8 https://t.me/mathtabletalks/2104 ,
... формула суммирования Пуассона, теорема Горбачёва-Кона-Элкиса и доказательства оптимальности Вязовской https://t.me/mathtabletalks/2173
Комплексная динамика, продолжение (множество Жюлиа как множество хаотической динамики, метод Ньютона и открытые множества с общей границей, главная кардиоида и кролик Дуади) — https://t.me/mathtabletalks/2235
Комплексная динамика, продолжение (параболическая точка и динамика рядом с ней, бифуркация удвоения периода и логистическое отображение) https://t.me/mathtabletalks/2329
Комплексная динамика, продолжение (переход в другие гиперболические компоненты, диск Зигеля, КАМ-теория и щели Кирквуда, множества Жюлиа положительной меры и алгоритмическая неразрешимость) — https://t.me/mathtabletalks/2454
"Трёхглавый дракон", начало —
https://t.me/mathtabletalks/2562
Окончание комплексной динамики: ренормализация и универсальность Фейгенбаума-Куле-Трессера — https://t.me/mathtabletalks/2619
Кривая Веронезе и выпуклые многогранники https://t.me/mathtabletalks/2692
Лекция Жиса и его "прогулка": теорема Концевича с билета в метро, Плутарх, Ньютон, доказательство Гаусса основной теоремы алгебры, алгебраические кривые и хордовые диаграммы — https://t.me/mathtabletalks/2699
Равносоставленность фигур — https://t.me/mathtabletalks/2807
Алиса и Боб: кто скорее разорился раньше? https://t.me/mathtabletalks/931
Слова Фибоначчи, квазикристаллы и фрактал Рози — https://t.me/mathtabletalks/948
Записки из Warwick-а
https://t.me/mathtabletalks/1053
Два взгляда на теорему о высотах в сферической геометрии (и на плоскости Лобачевского) — https://t.me/mathtabletalks/1080
Пара слов с Матпраздника — https://t.me/mathtabletalks/1123
... и рассказ о числах Мерсенна: как их проверяют на простоту? https://t.me/mathtabletalks/1129
Бильярды в треугольниках и не только — https://t.me/mathtabletalks/1178
Задача о пересылке бриллианта и применение эллиптических кривых в криптографии для защиты... https://t.me/mathtabletalks/1198
... и для нападения (алгоритм факторизации Ленстры) — https://t.me/mathtabletalks/1244
Игла Бюффона: как обойтись совсем без интегрирования — https://t.me/mathtabletalks/1264
Лекция Ингрид Добеши на ICM-2018: холсты из одного рулона (и кто бы мог подумать, что это можно будет проверить) — https://t.me/mathtabletalks/1279
Доказательство Ламберта иррациональности π: цепная дробь для тангенса (!) — https://t.me/mathtabletalks/1307
(и цепные дроби вообще, и небольшое упоминание фризов https://t.me/mathtabletalks/1402 )
... и последовательности Фарея https://t.me/mathtabletalks/1464
Премия Абеля — работы Фюрстенберга https://t.me/mathtabletalks/1514
Два слова о числах Каталана — https://t.me/mathtabletalks/1586
Абелевский сезон, продолжение — работы Маргулиса: https://t.me/mathtabletalks/1638
Факторизация: как работает метод квадратичного решета — начало (метод Диксона) https://t.me/mathtabletalks/1691 + окончание https://t.me/mathtabletalks/1716
Абелевский сезон-2, продолжение о работах Маргулиса: https://t.me/mathtabletalks/1727
Вспоминая Конвея:
лексикографические коды https://t.me/mathtabletalks/1750
несколько фотографий https://t.me/mathtabletalks/1791
программируя на FRACTRAN-е https://t.me/mathtabletalks/1797
статья о разных доказательствах иррациональности корня из двух — https://t.me/mathtabletalks/1803
(и отступление к доказательству рождественской теореме Ферма https://t.me/mathtabletalks/1822 )
статья "A Headache Causing Problem" https://t.me/mathtabletalks/1849
Катящиеся окружности и гипоциклоиды в них — https://t.me/mathtabletalks/1889
Рассказ о комплексной динамике, начало (когда множество Жюлиа связно?) —
https://t.me/mathtabletalks/1919
Уходя в далёкое прошлое — https://t.me/mathtabletalks/1943
Упаковки шаров: начало —https://t.me/mathtabletalks/2003
Кватернионы, вращения и правильные многогранники — https://t.me/mathtabletalks/2054
Упаковки шаров: продолжение — решётка E8 https://t.me/mathtabletalks/2104 ,
... формула суммирования Пуассона, теорема Горбачёва-Кона-Элкиса и доказательства оптимальности Вязовской https://t.me/mathtabletalks/2173
Комплексная динамика, продолжение (множество Жюлиа как множество хаотической динамики, метод Ньютона и открытые множества с общей границей, главная кардиоида и кролик Дуади) — https://t.me/mathtabletalks/2235
Комплексная динамика, продолжение (параболическая точка и динамика рядом с ней, бифуркация удвоения периода и логистическое отображение) https://t.me/mathtabletalks/2329
Комплексная динамика, продолжение (переход в другие гиперболические компоненты, диск Зигеля, КАМ-теория и щели Кирквуда, множества Жюлиа положительной меры и алгоритмическая неразрешимость) — https://t.me/mathtabletalks/2454
"Трёхглавый дракон", начало —
https://t.me/mathtabletalks/2562
Окончание комплексной динамики: ренормализация и универсальность Фейгенбаума-Куле-Трессера — https://t.me/mathtabletalks/2619
Кривая Веронезе и выпуклые многогранники https://t.me/mathtabletalks/2692
Лекция Жиса и его "прогулка": теорема Концевича с билета в метро, Плутарх, Ньютон, доказательство Гаусса основной теоремы алгебры, алгебраические кривые и хордовые диаграммы — https://t.me/mathtabletalks/2699
Равносоставленность фигур — https://t.me/mathtabletalks/2807
Victor Kleptsyn
13:07
Кстати, а вот тут бифуркация удвоения периода наблюдается для игрушечного дятла:
https://youtu.be/yjBPdkSvFPw?t=301
(спасибо Г. Мерзону за ссылку!)
https://youtu.be/yjBPdkSvFPw?t=301
(спасибо Г. Мерзону за ссылку!)
Victor Kleptsyn
13:17
In reply to this message
Да, давайте я добавлю пару слов — видео про Монстра совершенно замечательное: рассказ о группах как группах симметрий и как об абстрактном объекте, рассказ "с нуля" про серии групп и про спорадические группы, и заканчивается Монстром и той наименьшей размерностью, в которой он действует.
3blue1brown крут; снимаю шляпу!
3blue1brown крут; снимаю шляпу!
Victor Kleptsyn
28 August 2020
М
15:57
Математические байки
In reply to this message
Один из шагов при доказательстве теоремы Сабитова — это формула, выражающая объём симплекса через длины его рёбер; многомерный аналог формулы Герона. И на неё интересно посмотреть саму по себе.
Вот скриншот из видеозаписи лекции А. А. Гайфуллина в лаборатории Чебышева,
https://www.youtube.com/watch?v=L_DjieJPY8I :
Вот скриншот из видеозаписи лекции А. А. Гайфуллина в лаборатории Чебышева,
https://www.youtube.com/watch?v=L_DjieJPY8I :
Victor Kleptsyn
15:59
Сверху — классическая формула Герона, но в варианте с раскрытыми скобками; из этого вида видно, что квадрат площади — многочлен не только от длин сторон, но и от их квадратов.
Victor Kleptsyn
16:00
Снизу — общая формула; учтите, что тут А.А. обозначил через l_{ij} не длину ребра от P_i до P_j, а её квадрат.
Victor Kleptsyn
16:05
В частности — вот версия для объёма тетраэдра (тоже скриншот из видеозаписи, правда, в этот раз из курса в ЛШСМ — http://www.mathnet.ru/php/presentation.phtml?presentid=9386, — и тут l_{ij} обозначают просто длины, поэтому в определителе они возведены в квадрат):
Victor Kleptsyn
М
16:20
Математические байки
In reply to this message
А как такую формулу доказывать? Для начала давайте поймаем n!. А именно — если у нас есть n векторов в R^n, то объём симплекса, натянутого на эти вектора и начало координат, отличается от объёма натянутого на них же параллелограмма (иными словами, от составленного из них определителя) в n! раз.
Ибо площадь треугольника это половина произведения основания на высоту, объём тетраэдра это треть произведения высоты на площадь основания, и так далее — и вот и получается множитель
1/(n*(n-1)*...*2*1)= 1/n!
Ибо площадь треугольника это половина произведения основания на высоту, объём тетраэдра это треть произведения высоты на площадь основания, и так далее — и вот и получается множитель
1/(n*(n-1)*...*2*1)= 1/n!
Victor Kleptsyn
16:21
Это хорошо, но у нас-то (n+1) точка в R^n. Поэтому давайте возьмём их координаты и допишем к ним единицу в начало. Получится (n+1) вектор в R^{n+1} — и объём натянутого на них симплекса в (n+1)! раз меньше объёма натянутого на них же параллелепипеда. С другой стороны, этот же объём равен 1/(n+1) * объём исходного симплекса, потому что высота из вершины 0 равна 1: все остальные вершины живут в n-мерной плоскости x_1=1. Сокращая, получаем, что объём исходного симплекса равен (1/n!)*объём (n+1)-мерного параллелепипеда.
Victor Kleptsyn
16:35
Следующий шаг — квадраты сторон и квадрат объёма наводят на мысль о матрице Грама, матрице скалярных произведений векторов. А именно, если у нас есть n векторов в R^n, то матрица из их попарных скалярных произведений называется матрицей Грама, и её определитель равен квадрату объёма натянутого на них параллелепипеда.
Потому что если мы запишем наши векторы по столбцам матрицы M, то их матрица Грама будет задаваться как
G=M^* M,
и её определитель будет равен квадрату определителя M — то есть квадрату объёма.
Потому что если мы запишем наши векторы по столбцам матрицы M, то их матрица Грама будет задаваться как
G=M^* M,
и её определитель будет равен квадрату определителя M — то есть квадрату объёма.
Victor Kleptsyn
16:36
Но только пока получилось не совсем то, что надо: у матрицы Грама по диагонали стоят квадраты длин векторов, а вне диагонали скалярные произведения, а нам нужно, чтобы внутри подматрицы (n+1)x(n+1) стояли квадраты попарных расстояний между точками в R^n. Плюс, матрица у нас порядка (n+2), то есть явно, что работать нужно в R^{n+2}.
Victor Kleptsyn
16:43
Давайте посмотрим, а как эти квадраты расстояний через собственно координаты выражаются. Если у нас есть два вектора u и v, то
|u-v|^2 = <u-v,u-v> = |u|^2 + |v|^2 - 2 <u,v>
(можно сказать, что я записал банальную теорему косинусов).
|u-v|^2 = <u-v,u-v> = |u|^2 + |v|^2 - 2 <u,v>
(можно сказать, что я записал банальную теорему косинусов).
Victor Kleptsyn
16:43
А нельзя ли сделать из этого просто "скалярное произведение", только в R^{n+2}, и каких-то новых точек? Можно!
Запишем нужное нам выражение как
|u|^2 * 1 + 1* |v|^2 - 2<u,v>.
Запишем нужное нам выражение как
|u|^2 * 1 + 1* |v|^2 - 2<u,v>.
Victor Kleptsyn
16:44
А теперь любому вектору u из R^n сопоставим вектор в R^{n+2}, дописав к нему в начало не только 1 (как мы уже делали раньше), но и квадрат его длины:
u':=(1 , |u|^2 , u)
Тогда квадрат расстояния получается, как вычисление на u' и v' билинейной (и уже не положительно-определённой) формы D такого вида: перемножаем крест-накрест первые две координаты, и вычитаем удвоенное скалярное произведение остальных.
Вот её матрица:
u':=(1 , |u|^2 , u)
Тогда квадрат расстояния получается, как вычисление на u' и v' билинейной (и уже не положительно-определённой) формы D такого вида: перемножаем крест-накрест первые две координаты, и вычитаем удвоенное скалярное произведение остальных.
Вот её матрица:
Victor Kleptsyn
16:47
In reply to this message
У нас сейчас получился набор из (n+1) вектора в (n+2)-мерном пространстве, у которых все координаты, кроме второй, какие нужно, а вторую мы совсем не контролируем. Ну так добавим к этому набору (первым) вектор (0 1 0 0 ... 0). Тогда определитель из таких (n+2) векторов будет таким же, как определитель из (n+1) исходного вектора в (n+1)-мерном — который как раз равнялся (n! V).
Victor Kleptsyn
16:52
In reply to this message
Соберём из этих (n+2) векторов матрицу M и посмотрим на их матрицу Грама относительно билинейной формы D — иными словами, на
G = M^* D M.
Во-первых, это в точности та матрица, которая появляется на доске:
* D-скалярный квадрат (0 1 0000) равен нулю, потому что тут вторая координата вектора умножается на первую, а она равна 0
* его D-скалярное произведение с любым другим вектором набора равно 1, потому что у них у всех на первом месте стоит 1
* D-скалярные произведения остальных векторов друг с другом равны квадратам расстояний между вершинами симплекса — мы так наши вектора и произведение D строили.
G = M^* D M.
Во-первых, это в точности та матрица, которая появляется на доске:
* D-скалярный квадрат (0 1 0000) равен нулю, потому что тут вторая координата вектора умножается на первую, а она равна 0
* его D-скалярное произведение с любым другим вектором набора равно 1, потому что у них у всех на первом месте стоит 1
* D-скалярные произведения остальных векторов друг с другом равны квадратам расстояний между вершинами симплекса — мы так наши вектора и произведение D строили.
Victor Kleptsyn
16:53
С другой стороны, как и для обычной матрицы Грама, определитель G содержит квадрат определителя M — только в этот раз умноженный на det D:
Victor Kleptsyn
16:54
И вот (-1)^{n+1} и 2^n из формулы и появились — это определитель D. А раз мы уже знаем, что det M = n! V, то всё, формула Кэли-Менгера доказана. Ура!
Victor Kleptsyn
2 September 2020
М
16:34
Математические байки
В качестве затравки к следующей байке — задача:
Victor Kleptsyn
16:35
Десятая цифра после запятой у числа (sqrt{2}+sqrt{3})^100 это:
Final results
- 0 43 votes
- 1 5 votes
- 2 4 votes
- 3 3 votes
- 4 11 votes
- 5 11 votes
- 6 4 votes
- 7 7 votes
- 8 4 votes
- 9 36 votes
128 votes
Victor Kleptsyn
16:39
Задача честная — делается без калькулятора (а решение можно рассказать вообще без бумаги).
Victor Kleptsyn
М
20:16
Математические байки
Ещё одно начало истории: вот многим наверняка знакома классическая скатерть Улама. А именно — выписываем натуральные числа по спирали:
Victor Kleptsyn
20:18
И закрашиваем в этой спирали простые числа:
Victor Kleptsyn
20:21
Оказывается, что они часто выстраиваются вдоль диагоналей; вот скатерть Улама в квадрате 200x200 — https://commons.wikimedia.org/wiki/File:Ulam_1.png
Victor Kleptsyn
20:22
А вот фотография скатерти Улама из столовой МЦНМО/НМУ (спасибо Г. Мерзону за фотографии!) —
Victor Kleptsyn
20:36
Так вот, обычную скатерть Улама наверняка многие видели. А что будет, если её начать не с 1, а с другого числа — а именно, с числа 41?
Victor Kleptsyn
20:38
Вот так будет выглядеть начальный участок:
Victor Kleptsyn
20:40
Вот так — участок побольше:
Victor Kleptsyn
2 September 2020
М
20:42
Математические байки
Вот так — ещё побольше:
Victor Kleptsyn
20:45
И явно видна диагональ:
Victor Kleptsyn
20:46
А что ей соответствует? И будет ли так продолжаться и дальше?
Victor Kleptsyn
4 September 2020
М
19:36
Математические байки
Н
Непрерывное математическое образование 03.09.2020 17:54:39
http://www.mathnet.ru/present14521
С.К.Смирнову исполняется сегодня 50 лет
вот можно послушать, например, как он рассказывает на ЛШСМ-2016 про то, сколько можно нарисовать по клеточкам несамопересекающих кривых длины n и как выглядит типичная такая кривая — это оказывается связанным со статистической физикой, комплексным анализом и проч. — при этом сама лекция элементарна и доступна школьникам
С.К.Смирнову исполняется сегодня 50 лет
вот можно послушать, например, как он рассказывает на ЛШСМ-2016 про то, сколько можно нарисовать по клеточкам несамопересекающих кривых длины n и как выглядит типичная такая кривая — это оказывается связанным со статистической физикой, комплексным анализом и проч. — при этом сама лекция элементарна и доступна школьникам
Victor Kleptsyn
М
19:41
Математические байки
(Лекция, кстати, действительно была великолепная.)
Victor Kleptsyn
5 September 2020
М
18:20
Математические байки
In reply to this message
Давайте я начну с чуть более простого вопроса: какие первые несколько цифр после запятой у числа (1+sqrt{2})^100?
Victor Kleptsyn
18:21
Давайте раскроем скобки: получится какое-то выражение вида A+B\sqrt{2}, где A и B — огромные целые числа. Казалось бы, с таким не очень поработаешь.
Victor Kleptsyn
18:25
Но — когда мы работаем с комплексными числами, там есть комплексное сопряжение, заменяющее i на (-i): один корень уравнения z^2=-1 на другой. А что, если мы попробуем заменить \sqrt{2} на -\sqrt{2} — один корень уравнения x^2=2 на другой?
Victor Kleptsyn
18:27
Число (1+\sqrt{2}) заменится на число (1-\sqrt{2}), и несложно видеть, что
(1-\sqrt{2})^100 = A - B \sqrt{2}.
Тут можно просто проследить раскрытие скобок, а можно сказать, что такая замена — автоморфизм поля
Q[\sqrt{2}]={a+b\sqrt{2}| a, b\in Q}.
(1-\sqrt{2})^100 = A - B \sqrt{2}.
Тут можно просто проследить раскрытие скобок, а можно сказать, что такая замена — автоморфизм поля
Q[\sqrt{2}]={a+b\sqrt{2}| a, b\in Q}.
Victor Kleptsyn
18:31
Давайте теперь эти два числа сложим:
(1+\sqrt{2})^100 + (1-\sqrt{2})^100 = 2A.
Но второе слагаемое безумно маленькое: |1-\sqrt{2}|=0.41...<1/2, так что
0< (1-\sqrt{2})^100 < 1/2^100 < 1/10^30.
(И положительное, потому что степень 100 чётная.)
(1+\sqrt{2})^100 + (1-\sqrt{2})^100 = 2A.
Но второе слагаемое безумно маленькое: |1-\sqrt{2}|=0.41...<1/2, так что
0< (1-\sqrt{2})^100 < 1/2^100 < 1/10^30.
(И положительное, потому что степень 100 чётная.)
Victor Kleptsyn
18:34
Значит,
(1+\sqrt{2})^100 = 2A - (1-\sqrt{2})^100 = *,999999999999*
(где можно обещать как минимум 30 девяток).
(1+\sqrt{2})^100 = 2A - (1-\sqrt{2})^100 = *,999999999999*
(где можно обещать как минимум 30 девяток).
Victor Kleptsyn
18:35
А вот значение (спасибо WolframAlpha — https://www.wolframalpha.com/input/?i=%281%2B%5Csqrt%7B2%7D%29%5E100 )
189482250299273866835746159841800035873,999999999999999999999999999999999999994722460819308560...
189482250299273866835746159841800035873,999999999999999999999999999999999999994722460819308560...
Victor Kleptsyn
18:37
Поэтому число (1+\sqrt{2})^100 — почти целое, но не с кучей нулей, а с кучей девяток после запятой. А вот если бы я спросил про (1+\sqrt{2})^99, то вот там после запятой пошли бы нули, потому что (1-\sqrt{2})^99 — безумно маленькое, но отрицательное.
Victor Kleptsyn
М
18:53
Математические байки
Кстати — такое же рассуждение проходит и в некоторых других ситуациях. Например, для большой степени золотого сечения
\phi = (1+\sqrt{5})/2.
\phi = (1+\sqrt{5})/2.
Victor Kleptsyn
М
20:01
Математические байки
Более того, пусть у нас есть многочлен
P(z)=z^n+a_{n-1}z^{n-1}+...+a_1 z+a_0
с целыми коэффициентами и старшим коэффициентом 1. Тогда сумма k-ых степеней его корней — всегда целое число (что, кстати, хорошее упражнение). Значит, если у многочлена P(z) только один корень z_1 по модулю больше 1, а все остальные по модулю меньше единицы, то степени (z_1)^k этого корня становятся всё ближе и ближе к целым числам.
Такие числа называют числами Пизо (Pisot numbers): https://en.wikipedia.org/wiki/Pisot%E2%80%93Vijayaraghavan_number
Кстати, число Трибоначчи — вещественный корень уравнения x^3=x^2+x+1, равный 1.839... — как раз таково (потому что два других корня комплексно-сопряжённые, а произведение всех трёх корней равно 1.
P(z)=z^n+a_{n-1}z^{n-1}+...+a_1 z+a_0
с целыми коэффициентами и старшим коэффициентом 1. Тогда сумма k-ых степеней его корней — всегда целое число (что, кстати, хорошее упражнение). Значит, если у многочлена P(z) только один корень z_1 по модулю больше 1, а все остальные по модулю меньше единицы, то степени (z_1)^k этого корня становятся всё ближе и ближе к целым числам.
Такие числа называют числами Пизо (Pisot numbers): https://en.wikipedia.org/wiki/Pisot%E2%80%93Vijayaraghavan_number
Кстати, число Трибоначчи — вещественный корень уравнения x^3=x^2+x+1, равный 1.839... — как раз таково (потому что два других корня комплексно-сопряжённые, а произведение всех трёх корней равно 1.
Victor Kleptsyn
20:09
In reply to this message
Ну и уже понятно, что делать с исходным вопросом. А именно — если добавить к (\sqrt{2}+\sqrt{3})^100 такую же степень разности (\sqrt{2}-\sqrt{3})^100, то получится целое число. А сотая степень разности опять очень маленькая и положительная — поэтому десятая цифра после запятой у (\sqrt{2}+\sqrt{3})^100 это девятка (как и девять предыдущих и даже больше последующих):
(\sqrt{2}+\sqrt{3})^100 = 60189565958534864246850581634349698760897425062497,
9999999999999999999999999999999999999999999999999
83385824701096714433932...
(\sqrt{2}+\sqrt{3})^100 = 60189565958534864246850581634349698760897425062497,
9999999999999999999999999999999999999999999999999
83385824701096714433932...
Victor Kleptsyn
20:14
Следующий вопрос-затравка: а что можно сказать о первых цифрах после запятой у чисел
exp(π\sqrt{163}),
exp(π\sqrt{67})
и
exp(π\sqrt{43}) ?
exp(π\sqrt{163}),
exp(π\sqrt{67})
и
exp(π\sqrt{43}) ?
Victor Kleptsyn
20:16
Этот вопрос в смысле того, что за ним стоит, более сложный — где-то эдак порядка на два. 🙂
Но что точно можно, так это скормить все три выражения какому-нибудь компьютерному способу их посчитать, и посмотреть на результат. Думаю, станет достаточно ясно, что "таких совпадений — не бывает!".
Но что точно можно, так это скормить все три выражения какому-нибудь компьютерному способу их посчитать, и посмотреть на результат. Думаю, станет достаточно ясно, что "таких совпадений — не бывает!".
Victor Kleptsyn
М
21:46
Математические байки
In reply to this message
Ещё про код Хэмминга — совершенно прекрасное видео от 3blue1brown в двух частях:
https://www.youtube.com/watch?v=X8jsijhllIA +
https://www.youtube.com/watch?v=b3NxrZOu_CE
https://www.youtube.com/watch?v=X8jsijhllIA +
https://www.youtube.com/watch?v=b3NxrZOu_CE
Victor Kleptsyn
9 September 2020
М
13:58
Математические байки
Н
Непрерывное математическое образование 09.09.2020 00:07:01
онлайн-школа по топологии и геометрии и приложениям с пятницы по воскресенье https://cs.hse.ru/ata-lab/tga
Victor Kleptsyn
М
18:00
Математические байки
Н
Непрерывное математическое образование 08.09.2020 15:09:18
Vaughan Jones (31.12.1952–06.09.2020)
новозеландский математик, лауреат премии Филдса; многие слышали, надо полагать, про полином Джонса узла
«In 1984 Jones discovered an astonishing relationship between von Neumann algebras and geometric topology. As a result, he found a new polynomial invariant for knots and links in 3-space. (…) As time went on, it became clear that his discovery had to do in a bewildering variety of ways with widely separated areas of mathematics and physics (…). These included (in addition to knots and links) that part of statistical mechanics having to do with exactly solvable models, the very new area of quantum groups, and also Dynkin diagrams and the representation theory of simple Lie algebras. The central connecting link in all this mathematics was a tower of nested algebras which Jones had discovered some years earlier in the course of proving a theorem which is known as the “Index Theorem”.»
новозеландский математик, лауреат премии Филдса; многие слышали, надо полагать, про полином Джонса узла
«In 1984 Jones discovered an astonishing relationship between von Neumann algebras and geometric topology. As a result, he found a new polynomial invariant for knots and links in 3-space. (…) As time went on, it became clear that his discovery had to do in a bewildering variety of ways with widely separated areas of mathematics and physics (…). These included (in addition to knots and links) that part of statistical mechanics having to do with exactly solvable models, the very new area of quantum groups, and also Dynkin diagrams and the representation theory of simple Lie algebras. The central connecting link in all this mathematics was a tower of nested algebras which Jones had discovered some years earlier in the course of proving a theorem which is known as the “Index Theorem”.»
Victor Kleptsyn
18:00
Н
Непрерывное математическое образование 08.09.2020 16:46:37
http://mi.mathnet.ru/mp41
в качестве введения в тему узлов и их инвариантов (в т.ч. полинома Джонса) — статья Дужина и Чмутова в Мат. просвещении
в качестве введения в тему узлов и их инвариантов (в т.ч. полинома Джонса) — статья Дужина и Чмутова в Мат. просвещении
Victor Kleptsyn
М
18:27
Математические байки
Полином Джонса — инвариант узла, который даёт даже не число, а целый многочлен. Правда, тут нужно добавить, что многочлен не просто, а многочлен Лорана, то есть с отрицательными степенями; более того, для зацеплений — если связных компонент несколько — он становится многочленом от t^{1/2} (а именно, если компонент нечётное число, то в полиноме Джонса есть только целые степени, а если чётное, то только полуцелые).
Victor Kleptsyn
18:30
In reply to this message
Я в какой-то момент тут писал про другой инвариант узла, число правильных трёхцветных раскрасок. Это число, например, позволяет доказать, что узел-трилистник нельзя развязать (ибо значения инварианта на трилистнике и на незаузленной окружности разные). Но число трёхцветных раскрасок не может отличить узел от его зеркального отражения — так что правый трилистник от левого оно не отличает. А полином Джонса — отличает!
Victor Kleptsyn
М
18:47
Математические байки
Для одного из них он равен t+t^3-t^4, а для другого t^{-1}+t^{-3}-t^{-4}. Поскольку эти полиномы разные — то и узлы разные.
Кстати, отсюда легко угадать, что при зеркальном отражении узла (или зацепления) в полиноме Джонса t заменяется на t^{-1}.
Кстати, отсюда легко угадать, что при зеркальном отражении узла (или зацепления) в полиноме Джонса t заменяется на t^{-1}.
Victor Kleptsyn
М
19:33
Математические байки
Для меня полином Джонса был одним из первых знакомств с "большой математикой". На Летней Конференции Турнира Городов в 1996 году в Угличе одна из задач была посвящена как раз инвариантам — сначала кривых на плоскости, которые нельзя "ломать", а потом и инвариантам узлов:
Victor Kleptsyn
19:39
Отсюда — https://www.turgor.ru/lktg/1996/lktg1996.pdf ;
Алексей Брониславович до сих пор вспоминает, как я его там оставил без десерта (поймав за обедом с вопросами обо всём об этом — так что десерт прошёл мимо него). А под конец лета я с упоением читал их с Прасоловым книгу "Узлы, зацепления, косы и трёхмерные многообразия" — https://www.mccme.ru/free-books/prasolov/knots.pdf
Алексей Брониславович до сих пор вспоминает, как я его там оставил без десерта (поймав за обедом с вопросами обо всём об этом — так что десерт прошёл мимо него). А под конец лета я с упоением читал их с Прасоловым книгу "Узлы, зацепления, косы и трёхмерные многообразия" — https://www.mccme.ru/free-books/prasolov/knots.pdf
Victor Kleptsyn
10 September 2020
М
19:04
Математические байки
Н
Непрерывное математическое образование 10.09.2020 19:04:22
поздравляем А.А.Логунова с премией New Horizons in Mathematics «For novel techniques to study solutions to elliptic equations, and their application to long-standing problems in nodal geometry.»
Victor Kleptsyn
М
22:32
Математические байки
Н
Непрерывное математическое образование 11.08.2020 00:16:54
в новом номере ТрВ-Науки — несколько материалов про лауреатов премии Европейского математического общества этого года
«Премия EMS — довольно хорошая молодежная премия, многие ее лауреаты достигают больших высот в математике. Среди лауреатов прошлых лет десятеро стали потом филдсовскими медалистами, в том числе Максим Концевич, Григорий Перельман, Андрей Окуньков и Станислав Смирнов; из математиков, работающих сейчас в Москве, эту премию получали еще Александр Кузнецов и Стефан Немировский. Оба лауреата нынешнего года российского происхождения получали премию Московского математического общества: Александр Ефимов в 2016, а Александр Логунов — в 2017 году.»
«Премия EMS — довольно хорошая молодежная премия, многие ее лауреаты достигают больших высот в математике. Среди лауреатов прошлых лет десятеро стали потом филдсовскими медалистами, в том числе Максим Концевич, Григорий Перельман, Андрей Окуньков и Станислав Смирнов; из математиков, работающих сейчас в Москве, эту премию получали еще Александр Кузнецов и Стефан Немировский. Оба лауреата нынешнего года российского происхождения получали премию Московского математического общества: Александр Ефимов в 2016, а Александр Логунов — в 2017 году.»
Victor Kleptsyn
М
22:36
Математические байки
In reply to this message
На всякий случай -- это я отфорвардил ещё августовское сообщение, но сейчас очень в тему.
Victor Kleptsyn
24 September 2020
М
18:59
Математические байки
Н
Непрерывное математическое образование 24.09.2020 18:54:13
файл книги Пьера Деорнуа про сюрреальные числа Конвея и другие игры (по его курсу на ЛШСМ) теперь доступен на странице https://mccme.ru/dubna/books/
купить бумажную книгу с цветными картинками тоже, разумеется, можно — https://biblio.mccme.ru/node/5911/shop
купить бумажную книгу с цветными картинками тоже, разумеется, можно — https://biblio.mccme.ru/node/5911/shop
Victor Kleptsyn
1 October 2020
М
19:59
Математические байки
Написал (https://nplus1.ru/material/2020/09/24/dodecahedron ) про недавние работы J. Athreya, D. Aulicino и P. W. Hooper о замкнутых геодезических "из вершины в себя" на додекаэдре — https://arxiv.org/abs/1802.00811 + https://arxiv.org/abs/1811.04131
Victor Kleptsyn
20:02
Довольно понятно, что такое геодезическая — локально кратчайшая линия, или, что то же самое, линия, идущая по прямой на каждой грани, а при переходе через ребро продолжающаяся так, чтобы на развёртке, где эти две грани развёрнуты на плоскость, выглядеть прямой:
Victor Kleptsyn
20:06
Ну и тут можно вспомнить задачу — кажется, из Гарднера? — про то, как мухе проползти по кубу по кратчайшему пути из вершины в диаметрально противоположную, и какой длины будет этот путь.
Victor Kleptsyn
20:07
А вот за вершину (если она в неё попадает) геодезическую продолжить нельзя — точно так же, как с траекториями в бильярде внутри многоугольника. Собственно, геодезические на многогранниках и бильярды в многоугольниках — исключительно близкие сюжеты.
Victor Kleptsyn
20:10
Так вот — вопрос был такой: а есть ли на каком-нибудь правильном многограннике "кругосветная" геодезическая, которая начинается и заканчивается в одной и той же вершине?
Victor Kleptsyn
20:20
Если бы речь шла просто о замкнутой геодезической, не заходящей в вершины вообще, то нет ничего легче. Скажем, квадратное сечение куба плоскостью, параллельной его грани. Или — что чуть интереснее — правильный шестиугольник, проходящий по серединам рёбер, который на нём высекает серединный перпендикуляр к одной из его пространственных диагоналей.
Victor Kleptsyn
20:24
Такой путь по серединам рёбер есть и на правильном додекаэдре — и вот тут можно его появление увидеть (там 20 секунд после временной отметки, и да, я очень советую это посмотреть):
https://www.youtube.com/watch?v=E15KN8_hpcE&feature=youtu.be&t=4611
https://www.youtube.com/watch?v=E15KN8_hpcE&feature=youtu.be&t=4611
Victor Kleptsyn
20:31
Тут резинка идёт по серединам рёбер (так что эта геодезическая аналогична правильному шестиугольнику на кубе) — и этот замкнутый путь можно увидеть на не совсем обычной развёртке додекаэдра:
Victor Kleptsyn
20:32
Интересно, что этот путь тут такой не один — а есть целый "цилиндр" параллельных замкнутых геодезических:
Victor Kleptsyn
20:34
И на границе мы попадаем в вершину — но не в одну, а сразу в пять, так что из сдвига такого пути "до упора" пример построить не получится.
Victor Kleptsyn
М
21:00
Математические байки
А вот можно ли устроить "кругосветное путешествие" из вершины в неё же по геодезической — без захода в другие вершины?
Из вариантов фабулы — многогранник это планета Маленького принца, где в одной из вершин живёт барашек, а в остальных посажены розы — так что нужно, чтобы траектория прямого бега барашка не попадала в розы. Или — в вершинах стоят дома математиков, и один из них выходит на утреннюю пробежку (не проснувшись и потому строго по прямой) — и, конечно, не хочет вламываться в чужие дома (а по нынешним временам можно говорить, что соблюдает дистанцию).
Из вариантов фабулы — многогранник это планета Маленького принца, где в одной из вершин живёт барашек, а в остальных посажены розы — так что нужно, чтобы траектория прямого бега барашка не попадала в розы. Или — в вершинах стоят дома математиков, и один из них выходит на утреннюю пробежку (не проснувшись и потому строго по прямой) — и, конечно, не хочет вламываться в чужие дома (а по нынешним временам можно говорить, что соблюдает дистанцию).
Victor Kleptsyn
М
21:34
Математические байки
То, что нельзя на тетраэдре, кубе, октаэдре, икосаэдре — уже было известно. И это работы Davis, Dods, Traub, Yang (https://arxiv.org/abs/1508.03546 ) для тетраэдра и куба и Д. Фукса (http://armj.math.stonybrook.edu/pdf-Springer-final/016-0040.pdf ) для октаэдра и икосаэдра.
Кстати — если помните "Математический дивертисмент" Табачникова и Фукса, то Фукс — тот самый (и учебник по гомотопической топологии с Фоменко это он же),
https://ru.wikipedia.org/wiki/%D0%A4%D1%83%D0%BA%D1%81,_%D0%94%D0%BC%D0%B8%D1%82%D1%80%D0%B8%D0%B9_%D0%91%D0%BE%D1%80%D0%B8%D1%81%D0%BE%D0%B2%D0%B8%D1%87
Кстати — если помните "Математический дивертисмент" Табачникова и Фукса, то Фукс — тот самый (и учебник по гомотопической топологии с Фоменко это он же),
https://ru.wikipedia.org/wiki/%D0%A4%D1%83%D0%BA%D1%81,_%D0%94%D0%BC%D0%B8%D1%82%D1%80%D0%B8%D0%B9_%D0%91%D0%BE%D1%80%D0%B8%D1%81%D0%BE%D0%B2%D0%B8%D1%87
Victor Kleptsyn
8 October 2020
М
12:43
Математические байки
In reply to this message
Давайте продолжим?
Да, обе фабулы выше (утренняя пробежка и Маленький принц) я взял из вот этого видео Numberphile — https://youtu.be/G9_l8QASobI?t=153 ; а вот пара скриншотов оттуда:
Да, обе фабулы выше (утренняя пробежка и Маленький принц) я взял из вот этого видео Numberphile — https://youtu.be/G9_l8QASobI?t=153 ; а вот пара скриншотов оттуда:
Victor Kleptsyn
12:47
In reply to this message
Так вот — история состоит в том, что на додекаэдре такое кругосветное путешествие из вершины в себя без захода в другие вершины оказывается возможным. И J. Athreya, D. Aulicino и P. W. Hooper не только нашли одну такую траекторию — но и расклассифицировали их все (а их оказывается бесконечное число).
Victor Kleptsyn
12:49
Вот самая простая такая траектория:
Victor Kleptsyn
12:58
Это не совсем стандартная развёртка, зато на ней траектория состоит из одного отрезка. Можно её нарисовать и на стандартной развёртке — тогда будет два отрезка:
Victor Kleptsyn
13:02
Да, это бесконечное количество траекторий делится на 31 "класс эквивалентности" — и вот тут (http://userhome.brooklyn.cuny.edu/aulicino/dodecahedron/join_closed_sc_figs.pdf ) они собрали представителей всех этих классов. Так что можно распечатывать, вырезать и склеивать 🙂
Victor Kleptsyn
13:09
In reply to this message
Ещё два примера из той же статьи (да, если что, на arXiv-е есть соответствующий препринт, https://arxiv.org/abs/1811.04131 ) —
Victor Kleptsyn
13:16
Но давайте я до рассказа про классификацию скажу, почему таких траекторий нет на остальных платоновых телах. Самый простой случай это тетраэдр.
Victor Kleptsyn
13:18
Давайте докажем, что на нём любая траектория из вершины в вершину обязана соединять две разных вершины. Для этого "прокатим" тетраэдр по плоскости, "отпечатывая" каждую грань и очередной отрезок траектории. Получится часть треугольной решётки (которую отпечатают грани), и отрезок из вершины в вершину на ней:
Victor Kleptsyn
13:22
In reply to this message
Но дело в том, что мы знаем, какая вершина окажется в каком узле. Потому что если перекатывать тетраэдр вообще всеми возможными способами — в вершину решётки всегда будет приходить одна и та же вершина тетраэдра; собственно, как это и отмечено на рисунке выше.
А вершины с одинаковыми пометками образуют увеличенную вдвое подрешётку — так что середина отрезка, соединяющего две точки, соответствующие одной и той же вершине, это тоже вершина. И вот и противоречие — если бы мы хотели пройти "из A в A", то по пути мы обязательно наткнулись бы на другую вершину, а нам это запрещено.
А вершины с одинаковыми пометками образуют увеличенную вдвое подрешётку — так что середина отрезка, соединяющего две точки, соответствующие одной и той же вершине, это тоже вершина. И вот и противоречие — если бы мы хотели пройти "из A в A", то по пути мы обязательно наткнулись бы на другую вершину, а нам это запрещено.
Victor Kleptsyn
13:25
Увы, буквально это рассуждение для других многогранников не работает. А именно, если перекатывать по плоскости, скажем, куб — то конечно, все его "отпечатки граней" образуют квадратную решётку, но мы уже не знаем, какая вершина в какую точку решётки придёт, это зависит от пути перекатывания.
Victor Kleptsyn
13:39
С этим можно бороться двумя способами. Можно сказать, что мы перекатываем не абы как, а "по прямой". И использовать это для аккуратного описания того, как именно будет происходить "перекатывание" и какие же вершины где будут отпечатываться. Более-менее так, насколько я понимаю, прошли Davis, Dods, Traub, Yang (https://arxiv.org/pdf/1508.03546.pdf ) случай куба и Фукс (http://armj.math.stonybrook.edu/pdf-Springer-final/016-0040.pdf ) случай октаэдра и икосаэдра.
Victor Kleptsyn
13:52
А второй способ придумали как раз Athreya, Aulicino и Hooper, и он очень изящный. Итак, пусть на каком-то из многогранников, кроме додекаэдра, есть траектория из вершины в вершину. Прокатим его вдоль этой траектории, отпечатывая грани (и саму траекторию) на плоскости. На плоскости получится часть либо треугольной (тетраэдр, октаэдр, икосаэдр), либо квадратной (куб) решётки. И отрезок (отпечаток траектории), соединяющий две вершины (A и B ) этой решётки.
А теперь давайте посмотрим на середину C этого отрезка. Во-первых, на плоскости центральная симметрия относительно C переводит A в B, и поэтому сохраняет решётку (потому что вектора под действием центральной симметрии просто меняют знак, поэтому достаточно, чтобы одна точка решётки перешла в точку решётки). А это значит, что эта точка в случае треугольной решётки может быть либо вершиной, либо серединой ребра — а в случае квадратной либо вершиной, либо серединой ребра, либо серединой грани.
А теперь давайте посмотрим на середину C этого отрезка. Во-первых, на плоскости центральная симметрия относительно C переводит A в B, и поэтому сохраняет решётку (потому что вектора под действием центральной симметрии просто меняют знак, поэтому достаточно, чтобы одна точка решётки перешла в точку решётки). А это значит, что эта точка в случае треугольной решётки может быть либо вершиной, либо серединой ребра — а в случае квадратной либо вершиной, либо серединой ребра, либо серединой грани.
Victor Kleptsyn
13:54
Вершиной она быть не может — потому что траектория в другие вершины не заходит. Остаются только середины рёбер в случае треугольной решётки, и середины рёбер и граней в случае квадратной. В любом случае — рассмотрим ту точку многогранника C', которая "отпечаталась" в C, и рассмотрим поворот на 180 градусов вокруг прямой OC', где O — центр многогранника. (Другими словами — мы пытаемся "поднять" исходную центральную симметрию на многогранник)
Victor Kleptsyn
13:56
В каждом из этих случаев (середина ребра тетраэдра, середина ребра или грани куба) мы получаем движение многогранника, которое сохраняет точку C' и переводит отрезок траектории рядом с ней в себя. А значит, эта симметрия переводит в себя и всю траекторию.
Victor Kleptsyn
13:58
В частности, она меняет местами её начальную и конечную вершину. Но у каждой из этих центральных симметрий нет вершин, которые она бы могла сохранить: неподвижные точки у осевой симметрии это только точки на оси, а ни одна из упомянутых осей через вершины не проходит. Поэтому начальная и конечная вершины траектории совпадать не могут.
Ура, победа!
Ура, победа!
Victor Kleptsyn
13:58
(И мне это рассуждение очень нравится, оно очень изящное.)
Victor Kleptsyn
М
14:38
Математические байки
А вот работа с додекаэдром оказалась связанной с теорией очень плоских (или трансляционных ) поверхностей. Такая поверхность получается так: берём один или несколько многоугольников на плоскости, у которых в сумме чётное число сторон. И предположим, что эти стороны разбиты на пары, совмещаемые параллельными переносами (отсюда название "трансляционные"), причём многоугольники при таком совмещении оказываются по разные стороны от этих сторон. Тогда — склеим все эти пары. Получится поверхность, и она действительно "плоская" — кроме вершин.
А вот в вершинах могут собираться "конические особенности" (только с углом больше, а не меньше 2π, как в привычном нам конусе). Скажем, если такую процедуру проделать с восьмиугольником, то все 8 вершин в результате склейки станут одной и той же вершиной, а полный угол в ней будет 8*(3π/4) = 6π.
А вот в вершинах могут собираться "конические особенности" (только с углом больше, а не меньше 2π, как в привычном нам конусе). Скажем, если такую процедуру проделать с восьмиугольником, то все 8 вершин в результате склейки станут одной и той же вершиной, а полный угол в ней будет 8*(3π/4) = 6π.
Victor Kleptsyn
М
16:33
Математические байки
Собственно, самый простой пример такой поверхности — это тор, склеенный из квадрата или прямоугольника (или даже из параллелограмма); собственно, в старых видеоиграх часто персонажи, уходящие за один край экрана, тотчас же возвращались через другой:
Victor Kleptsyn
21 October 2020
М
15:47
Математические байки
In reply to this message
Продолжим?
Собственно, в прошлый раз я остановился на самом интересном месте — на том, что остался додекаэдр, на котором "кругосветные путешествия" из вершины в себя таки есть. А как их искать и описывать, и при чём тут трансляционные поверхности?
Собственно, в прошлый раз я остановился на самом интересном месте — на том, что остался додекаэдр, на котором "кругосветные путешествия" из вершины в себя таки есть. А как их искать и описывать, и при чём тут трансляционные поверхности?
Victor Kleptsyn
15:47
Вообще, трансляционные поверхности возникают и в этой задаче, и в бильярдах в многоугольниках, из одного и того же рассуждения. Когда мы запускаем траекторию по многограннику — мы можем "прокатывать" вдоль неё многогранник, получая прямую на плоскости и приставленные друг к другу "отпечатки" граней. Когда мы запускаем бильярдную траекторию в многоугольнике — её тоже можно сделать прямой, достраивая отражением за каждой гранью.
Victor Kleptsyn
15:53
Скажем, вот траектория бильярда в равнобедренном прямоугольном треугольнике, выходящая из одной вершины и попадающая в другую (спасибо М. Панову за изображения!) :
Victor Kleptsyn
15:54
А вот она же, но после многих достраиваний отражённых областей:
Victor Kleptsyn
15:55
Так вот: давайте строить все вообще "отпечатки", перекатывая многогранник всеми возможными способами. Или для бильярда — брать вообще все возможные композиции отражений исходной области.
Понятно, что их будет бесконечно много, они будут накладываться друг на друга, и вообще получающийся объект будет ужасен. Но.
Если вдруг какие-то две области отличаются на параллельный перенос — так отождествим их! Потому что, кроме этого параллельного переноса, их ничего не отличает друг от друга, и всё, что мы можем получить из одной, мы (летя вдоль параллельно перенесённого луча) получим и из другой.
Понятно, что их будет бесконечно много, они будут накладываться друг на друга, и вообще получающийся объект будет ужасен. Но.
Если вдруг какие-то две области отличаются на параллельный перенос — так отождествим их! Потому что, кроме этого параллельного переноса, их ничего не отличает друг от друга, и всё, что мы можем получить из одной, мы (летя вдоль параллельно перенесённого луча) получим и из другой.
Victor Kleptsyn
15:56
Так вот — если все углы у нас были соизмеримы с π (во всех гранях многогранника или в многоугольнике, где у нас бильярд) — то после такого отождествления останется лишь конечное число областей.
А это и есть трансляционная (или "очень плоская") поверхность.
А это и есть трансляционная (или "очень плоская") поверхность.
Victor Kleptsyn
15:57
В качестве паузы — видео (тоже спасибо М. Панову!) более сложной траектории бильярда, тоже в равнобедренном прямоугольном треугольнике:
Victor Kleptsyn
15:57
Правда, красиво?
Victor Kleptsyn
16:05
Так вот — из правильных многогранников и из бильярдов в "рациональных" (все углы вида (p/q)π) многоугольниках мы научились получать трансляционные поверхности. Например, из бильярда в треугольнике с углами π/8, 3π/8, π/2 получится восьмиугольник со склеенными противоположными сторонами.
Victor Kleptsyn
16:08
А вот скриншот из видеозаписи лекции Антона Зорича на летней школе "Алгебра и геометрия" в Ярославле в 2013 году,
http://www.mathnet.ru/php/presentation.phtml?option_lang=rus&presentid=9994 , где Антон как раз эту задачу разбирает:
http://www.mathnet.ru/php/presentation.phtml?option_lang=rus&presentid=9994 , где Антон как раз эту задачу разбирает:
Victor Kleptsyn
16:15
(Да, если что, эту и следующую лекции — http://www.mathnet.ru/php/presentation.phtml?option_lang=rus&presentid=9998 — я очень советую, так же, как и лекцию Антона на Глобусе: http://www.mathnet.ru/php/seminars.phtml?presentid=15424 )
Victor Kleptsyn
М
16:31
Математические байки
In reply to this message
Кстати — очень хорошее упражнение это понять, что при такой склейке сторон из восьмиугольника получается сфера с двумя ручками (а все восемь его вершин становятся одной и той же, в которую "собирается" полный угол в аж 6π).
Victor Kleptsyn
16:33
Если возвращаться к додекаэдру — то, чтобы описать пути на нём, нам понадобится отпечатать каждую грань (а мы должны помнить, какая именно грань отпечатывается, чтобы знать, какие вершины будем соединять, и отождествлять только сдвиги одной и той же грани) каждым из 10 способов — потому что "прокатывание" додекаэдра вокруг вершины поворачивает его на π/5 = (1/10) от полного оборота.
Victor Kleptsyn
16:38
Получается конструкция из 10*12=120 пятиугольников; на самом деле, конечно, можно их объединить в 10 развёрток (как раз каждая грань появляется по одному разу), поворачиваемых друг относительно друга на (1/10) оборота:
Victor Kleptsyn
16:43
Казалось бы, совершенно жуткий объект. Но! На нём теперь нас интересуют просто прямые (ну, разве что при выходе через одну сторону они "влетают" через другую; собственно, на полной картинке — см. https://arxiv.org/pdf/1811.04131.pdf , с. 9 — отождествляемые стороны подписаны, но этих подписей так много, что без них картинка выглядит красивее).
Victor Kleptsyn
16:48
А ещё работу с траекториями на нём можно упрощать. Дело в том, что нас сейчас интересуют прямые и параллельность, но не интересуют углы. Поэтому если мы возьмём всю эту картинку и подействуем на неё аффинным преобразованием — то траектории перейдут в траектории, правда, на уже новой трансляционной поверхности.
Victor Kleptsyn
М
17:48
Математические байки
Казалось бы, если мы подействуем "сильно нетривиальным" аффинным преобразованием — скажем, сожмём всю картинку по оси ординат в 100 раз и растянем в те же 100 раз по оси абсцисс — то из всех пятиугольников получатся этакие "медузы". Но. "Развёртка" у плоской поверхности не единственная — можно где-нибудь разрезать (создав этим новую пару отождествляемых сторон), перенести кусочки, приставить по отождествляемым сторонам и склеить. И "часто" из "сильно сплющенной" картинки можно восстановить опять "разумно выглядящую".
Более того, можно пытаться так делать, сокращая геодезическую (сжимая в её направлении и растягивая в перпендикулярном, чтобы площадь не менять).
Более того, можно пытаться так делать, сокращая геодезическую (сжимая в её направлении и растягивая в перпендикулярном, чтобы площадь не менять).
Victor Kleptsyn
17:51
In reply to this message
Например:
Теорема. На склеенном из квадрата торе любую замкнутую геодезическую можно правильным аффинным преобразованием превратить в просто идущую вдоль ребра, а тор останется таким же, каким был.
Теорема. На склеенном из квадрата торе любую замкнутую геодезическую можно правильным аффинным преобразованием превратить в просто идущую вдоль ребра, а тор останется таким же, каким был.
Victor Kleptsyn
17:54
Пример, он же начало доказательства —
Victor Kleptsyn
17:54
In reply to this message
Была (слева) чёрная геодезическая. Тор "накренили" преобразованием (x,y)->(x+y,y). После этого разрезали по красному пунктиру.
Victor Kleptsyn
17:55
Получили два треугольника — параллельно перенесли правый, приставив одну зелёную сторону к другой. Получили опять тор, склеенный из квадрата — но геодезическая уже стала проще.
Victor Kleptsyn
17:59
Точнее, тут она совсем упростилась — до искомого "идёт вдоль ребра". А если бы была какая-то более сложная геодезическая, то у неё был бы наклон p/q, под которым она шла, и на квадратной решётке она смещалась бы за свой период на q по оси Ox и на p по оси Oy. Ну так мы применим алгоритм Евклида — как раз преобразования
(x,y)->(x ± y, y) и (x,y)->(x, y ± x)
позволяют вычесть p из q или q из p.
(x,y)->(x ± y, y) и (x,y)->(x, y ± x)
позволяют вычесть p из q или q из p.
Victor Kleptsyn
18:08
In reply to this message
Так вот — возьмём ту поверхность, которая получается из додекаэдра. Из неё можно сделать гораздо более простую поверхность "двойного пятиугольника" П_5:
Victor Kleptsyn
18:11
In reply to this message
А именно — просто отправим все пятиугольники вершиной вверх в пятиугольник вершиной вверх тут, а вершиной вниз — в пятиугольник вершиной вниз тут. Получится разветвлённое (в вершинах) накрытие — но главное, что отображение состоит из параллельных переносов, так что оно "уважает" траектории.
Victor Kleptsyn
18:12
Вот траектория из вершины в (другую) вершину на одной развёртке додекаэдра — и её образ, траектория из вершины в вершину на П_5:
Victor Kleptsyn
18:18
Так вот — оказывается, что если смотреть только на П_5, то есть аналогичная теорема: все траектории "из вершины в вершину" можно аффинным преобразованием, переводящим П_5 в себя, перевести в одну из двух траекторий: либо вдоль ребра пятиугольника, либо вдоль диагонали:
Victor Kleptsyn
18:25
(Причём та, что вдоль ребра, нам на самом деле не подходит — из-за рассуждений с центральной симметрией, очень похожих на те, что уже были для всех остальных платоновых тел.)
Victor Kleptsyn
18:34
In reply to this message
Так вот — если у нас есть преобразование "внизу", на П_5, оно вовсе не обязательно приходит "сверху", из преобразования всей огромной поверхности. В качестве аналогичного примера — на тор, склеенный из одного квадрата, можно подействовать любым преобразованием из SL(2,Z), и он перейдёт в себя. А вот поверхность, склеенную из нескольких квадратиков (с каким-то отождествлением пар параллельных сторон), такое преобразование вовсе не обязательно переведёт в себя. И вот пример — опять из лекции Антона:
Victor Kleptsyn
18:35
Справа отождествление сторон уже не такое, как слева.
Victor Kleptsyn
18:36
Но! Хоть "поднимается" и не всякое преобразование П_5 — те, которые поднимаются, в группе всех оказываются подгруппой конечного индекса.
Victor Kleptsyn
18:43
И получается такая цепочка: геодезические из вершины в вершину на додекаэдре — приходят из прямых лучей из вершины в вершину на "огромной поверхности". Прямой луч там проецируется в прямой луч из вершину в вершину на П_5, и на самом П_5 его можно было бы упростить аффинным преобразованием до одного из двух (ребро или диагональ). Увы, можно упрощать только преобразованием "огромной поверхности". Но такие преобразования образуют подгруппу конечного индекса — поэтому получается упростить луч до одного из конечного множества!
Victor Kleptsyn
18:43
Вывод — задача описания всех путей из вершины в вершину на додекаэдре сведена к конечному перебору. И ура!
Victor Kleptsyn
18:48
А ещё можно посмотреть на замкнутые геодезические на П_5, не проходящие через вершины, и на их кодирование и упрощение.
И тут я порекламирую прекрасное видео Дианы Дэвис, которое в 2012-м получило выиграло в категории "математика и физика" конкурс "Dance your PhD":
https://www.youtube.com/watch?v=FH28a7v_gDQ
И тут я порекламирую прекрасное видео Дианы Дэвис, которое в 2012-м получило выиграло в категории "математика и физика" конкурс "Dance your PhD":
https://www.youtube.com/watch?v=FH28a7v_gDQ
Victor Kleptsyn
18:48
Вот несколько кадров оттуда:
- действие аффинной группы —
- действие аффинной группы —
Victor Kleptsyn
18:49
Перестройка развёртки поверхности (отрезаем длинные "хвостики" и приносим ближе к центральной области) —
Victor Kleptsyn
18:50
Кодирование замкнутой геодезической и её образа при перестройке —
Victor Kleptsyn
18:52
В общем — совершенно классно сделано!
(До того, как я увидел это видео не увидел — если бы мне сказали, что можно станцевать геодезические на трансляционных поверхностях, я бы не поверил!)
(До того, как я увидел это видео не увидел — если бы мне сказали, что можно станцевать геодезические на трансляционных поверхностях, я бы не поверил!)
Victor Kleptsyn
18:59
И в завершение — ещё один результат, о котором рассказывал в тех лекциях Антон Зорич. Пусть на координатной плоскости периодически посажены прямоугольные деревья. Как в них будет запутываться "бильярдный" ветер — частичка, движущаяся по бильярду в их дополнении?
Victor Kleptsyn
19:01
Если бы деревьев не было, частица убежала бы на бесконечность с линейной скоростью. Броуновское движение типичным образом в момент времени t оказывается на расстоянии порядка корня из t от начала пути.
Victor Kleptsyn
19:01
А тут возникает показатель (2/3)!
Victor Kleptsyn
19:04
См. — Vincent Delecroix, Pascal Hubert, Samuel Lelièvre,
Diffusion for the periodic wind-tree model
https://arxiv.org/pdf/1107.1810.pdf
Diffusion for the periodic wind-tree model
https://arxiv.org/pdf/1107.1810.pdf
Victor Kleptsyn
19:13
И делается это опять через трансляционные поверхности и их преобразования. А именно — мы начинаем путь длины t сжимать, уменьшая его длину, и смотрим, как при этом перестраивается соответствующая поверхность. А подробнее это, пожалуй, тема для другого рассказа.
Victor Kleptsyn
22 October 2020
М
09:42
Математические байки
Какая планета наибольшую долю времени была ближайшей к Земле за последнюю тысячу лет?
Final results
- Меркурий 119 votes
- Венера 267 votes
- Марс 233 votes
- Юпитер 18 votes
637 votes
Victor Kleptsyn
09:44
(Немного сменим тему; понятно, что тысяча лет тут указана, чтобы вопрос был формально корректно поставлен — можно было бы и десять тысяч взять...)
Victor Kleptsyn
М
11:45
Математические байки
In reply to this message
Возвращаясь к многогранникам и бильярдам — помните, как мы доказывали, что на правильном тетраэдре нет траектории из вершины в себя? Точно так же доказывается, что если в бильярде в равнобедренном прямоугольном треугольнике выпустить траекторию из одного из острых углов — обратно в него она вернуться не сможет. Вот в другой угол — пожалуйста; собственно, одну такую траекторию мы уже видели:
Victor Kleptsyn
11:47
Потому что — достроим все возможные отражения треугольника, чтобы бильярдная траектория стала прямой:
Victor Kleptsyn
11:50
Если мы достроим отражения не только вдоль траектории, а все вообще, получится решётка — на которой образы исходного острого угла образуют вдвое более крупную подрешётку. А тогда любой отрезок, их соединяющий, раньше пройдёт через другую вершину — через середину:
Victor Kleptsyn
11:53
И это в точности то же рассуждение, которое мы уже видели раньше — только там оно было для получающейся из правильного тетраэдра решётки из правильных треугольников.
Victor Kleptsyn
11:55
In reply to this message
И в статье Токарского именно из этого свойства доказывается, что источник света в одной точке не может осветить другую.
Victor Kleptsyn
11:57
Собственно, вот кусочек с этой леммой —
Victor Kleptsyn
12:02
А вся область состоит из отражений одного такого треугольника — причём точки A_0 и A_1 обе получаются из одного и того же острого угла:
Victor Kleptsyn
12:07
Несложно видеть, что траектории из A_0 строго по горизонтали, вертикали или под 45 градусов сразу же утыкаются в вершины (и потому не продолжаются).
А все остальные траектории можно "уронить" на один треугольник ABC, отправив туда все треугольнички последовательностью отражений — и получить бильярдную траекторию. А мы уже знаем, что из вершины A в себя бильярдной траектории там нет.
А все остальные траектории можно "уронить" на один треугольник ABC, отправив туда все треугольнички последовательностью отражений — и получить бильярдную траекторию. А мы уже знаем, что из вершины A в себя бильярдной траектории там нет.
Victor Kleptsyn
12:12
In reply to this message
А вот картинка освещения в такой же, но с меньшим числом сторон, области (правда, в ней может возникнуть желание сказать, что "а давайте разрешим прямому лучу A_0 A_1 пройти "вдоль стены"). И тут будут освещены все точки, кроме A_1:
Victor Kleptsyn
12:19
In reply to this message
Напоследок — его же анимация, как лучи эту область заполняют:
Victor Kleptsyn
24 October 2020
М
16:20
Математические байки
t
tropical saint petersburg 22.10.2020 23:03:22
Математика Безиковича — квадрат Канторовского множества, неопределённые повторные интегралы и красивые картинки (20Мб) http://mathcenter.spb.ru/nikaan/book/besicovitch_math.pdf
Victor Kleptsyn
М
16:39
Математические байки
In reply to this message
А ещё Безикович придумал стратегию, дающую удивительный ответ в одной задаче о преследовании. Если меня не подводит память — я это узнал из лекции Плахова на финале олимпиады Шарыгина в 2017-м ( http://geometry.ru/olimp/2017.php ).
Собственно, основной темой лекции тогда была задача Какейя о том, внутри фигуры какой наименьшей площади можно развернуть (на 180 градусов) отрезок-"иголку". С удивительным, полученным Безиковичем, ответом, что площадь такой фигуры может быть сколь угодно малой: см. http://kvant.mccme.ru/1973/04/o_vrashchenii_otrezka.htm . Собственно, в тексте по ссылке выше коллеги про это пишут.
А ещё есть видео Numberphile об этой конструкции — кстати, очень простой — https://youtu.be/j-dce6QmVAQ ; а ещё — см. вот эту задачу на Элементах: https://elementy.ru/problems/2353/Zadacha_ob_igolke (думаю, конструкция Безиковича как раз будет в послесловии).
Собственно, основной темой лекции тогда была задача Какейя о том, внутри фигуры какой наименьшей площади можно развернуть (на 180 градусов) отрезок-"иголку". С удивительным, полученным Безиковичем, ответом, что площадь такой фигуры может быть сколь угодно малой: см. http://kvant.mccme.ru/1973/04/o_vrashchenii_otrezka.htm . Собственно, в тексте по ссылке выше коллеги про это пишут.
А ещё есть видео Numberphile об этой конструкции — кстати, очень простой — https://youtu.be/j-dce6QmVAQ ; а ещё — см. вот эту задачу на Элементах: https://elementy.ru/problems/2353/Zadacha_ob_igolke (думаю, конструкция Безиковича как раз будет в послесловии).
Victor Kleptsyn
16:49
Так вот — тот же самый Безикович получил удивительный ответ в задаче "о льве и человеке" (с аллюзией на римскую казнь): одна точка преследует другую в круге ("на арене"), причём скорости у них одинаковые, а вторая точка, естественно, пытается убежать. Одинаковые скорости это, конечно, спорное предположение, но допустим, что лев старый, а человек в отличной форме.
Victor Kleptsyn
16:57
Интуитивно хочется сказать, что лучшее, что может сделать человек, это убежать по прямой от льва на границу круга, после чего бежать вдоль границы.
Но в этом случае лев его поймает.
Но в этом случае лев его поймает.
Victor Kleptsyn
М
17:26
Математические байки
Способ ловли за льва — занять положение на радиусе, утыкающемся в человека, и бежать к человеку так, чтобы это свойство сохранялось.
Тогда (пусть скорости и радиус окружности единичные), если лев на расстоянии r от центра, то на парирование движения человека "по углу" ему хватает скорости в r по нормали к радиусу. А значит, на движение к человеку остаётся \sqrt{1-r^2}.
Тогда (пусть скорости и радиус окружности единичные), если лев на расстоянии r от центра, то на парирование движения человека "по углу" ему хватает скорости в r по нормали к радиусу. А значит, на движение к человеку остаётся \sqrt{1-r^2}.
Victor Kleptsyn
17:44
Так что для расстояния r(t) от центра до льва получаем дифференциальное уравнение:
dr/dt= \sqrt{1-r^2(t)}.
dr/dt= \sqrt{1-r^2(t)}.
Victor Kleptsyn
17:49
А это уравнение приходит к единице за конечное время. В качестве рукомахательного объяснения — разница 1-r убывает со скоростью, примерно равной корню из себя (потому что (1-r^2)=(1-r)(1+r), то есть примерно 2(1-r)). А корень из маленькой величины её сильно больше.
Если на это смотреть более строго, но почти школьными методами — можно посмотреть, за какое время лев приблизится к человеку от расстояния 1/2^k до расстояния 1/2^{k+1}. Ему для этого нужно пройти расстояние порядка 1/2^k со скоростью 1/2^(k/2), значит, время будет тоже порядка 1/2^(k/2). А значит, сумма таких времён оценивается убывающей геометрической прогрессией — и потому сходится.
Если на это смотреть более строго, но почти школьными методами — можно посмотреть, за какое время лев приблизится к человеку от расстояния 1/2^k до расстояния 1/2^{k+1}. Ему для этого нужно пройти расстояние порядка 1/2^k со скоростью 1/2^(k/2), значит, время будет тоже порядка 1/2^(k/2). А значит, сумма таких времён оценивается убывающей геометрической прогрессией — и потому сходится.
Victor Kleptsyn
17:52
На самом деле, ещё этот диффур можно просто явно решить, не задумываясь применив общий метод решения одномерных автономных уравнений первого порядка: превратив dr/dt = f(r) в dr/f(r) = dt, проинтегрировав и получив выражение для времени t через неизвестную r, после чего его обратив и найдя r.
А ещё можно угадать решение r(t)=sin t (ну и все его сдвиги, sin (t+C), раз система автономная) 🙂
Которое, естественно, в единицу обращается в конечный момент времени.
А ещё можно угадать решение r(t)=sin t (ну и все его сдвиги, sin (t+C), раз система автономная) 🙂
Которое, естественно, в единицу обращается в конечный момент времени.
Victor Kleptsyn
17:53
И ещё кстати, диффур для уровня воды, вытекающей из ванной, когда из неё достали пробку, такой же —
h'= – const* \sqrt{h}.
И его решение тоже уходит в 0 за конечное время. Но это я отклонился в сторону.
h'= – const* \sqrt{h}.
И его решение тоже уходит в 0 за конечное время. Но это я отклонился в сторону.
Victor Kleptsyn
18:00
Ну так вот — можно было бы предположить, что раз человек так ото льва не ушёл, он и вовсе не уйдет.
Ан нет! Безикович показал, что всё не так — что человек может убегать ото льва в круге неограниченно долго.
Ан нет! Безикович показал, что всё не так — что человек может убегать ото льва в круге неограниченно долго.
Victor Kleptsyn
18:12
Более того — оказывается, что алгоритм убегания для человека очень простой. Он состоит из бесконечного числа шагов следующего вида:
Шаг номер n
- провести прямую через себя и центр арены, посмотреть, по какую сторону от неё находится лев
- пробежать расстояние L_n перпендикулярно этой прямой в ту полуплоскость, где льва нет
Шаг номер n
- провести прямую через себя и центр арены, посмотреть, по какую сторону от неё находится лев
- пробежать расстояние L_n перпендикулярно этой прямой в ту полуплоскость, где льва нет
Victor Kleptsyn
18:12
(Мы тут предполагаем, что человек начинает не на границе — иначе пусть он сделает хотя бы один шаг внутрь, а потом уже запускает алгоритм.)
Victor Kleptsyn
18:14
In reply to this message
Тогда:
1) очевидно, что пока человек может делать эти шаги, лев его не поймает.
Потому что в проекции на направление, куда бежит человек, лев от него отстаёт (ну или хотя бы не нагоняет): проекция льва движется со скоростью, не большей 1, поскольку это проекция единичного вектора скорости.
2) Чтобы человек мог делать такие шаги неограниченно долго, нужно, чтобы сумма ряда \sum L_n расходилась.
(Иначе это к Зенону 🙂 )
3) За один шаг квадрат расстояния до центра возрастает на L_n^2.
(ибо теорема Пифагора: начинает бежать человек перпендикулярно радиусу)
Значит, нужно, чтобы сумма \sum L_n^2 сходилась — и её сумма, плюс квадрат начального радиуса, был бы меньше 1 (ну или квадрата радиуса арены).
1) очевидно, что пока человек может делать эти шаги, лев его не поймает.
Потому что в проекции на направление, куда бежит человек, лев от него отстаёт (ну или хотя бы не нагоняет): проекция льва движется со скоростью, не большей 1, поскольку это проекция единичного вектора скорости.
2) Чтобы человек мог делать такие шаги неограниченно долго, нужно, чтобы сумма ряда \sum L_n расходилась.
(Иначе это к Зенону 🙂 )
3) За один шаг квадрат расстояния до центра возрастает на L_n^2.
(ибо теорема Пифагора: начинает бежать человек перпендикулярно радиусу)
Значит, нужно, чтобы сумма \sum L_n^2 сходилась — и её сумма, плюс квадрат начального радиуса, был бы меньше 1 (ну или квадрата радиуса арены).
Victor Kleptsyn
18:15
Так вот — несложно увидеть, что такая последовательность L_n найдётся. Потому что достаточно взять гармонический ряд 1/n и умножить его на достаточно маленькую константу, чтобы было выполнена оценка для суммы квадратов.
Вот и всё!
Вот и всё!
Victor Kleptsyn
18:15
Правда, красивая конструкция?
Victor Kleptsyn
18:20
Кстати — возвращаясь к варианту, где человек движется только по граничной окружности: если человек движется всё время в одном и том же направлении, то "радиально" преследующий его лев будет двигаться по окружности вдвое меньшего радиуса.
Victor Kleptsyn
18:21
Картинка из вот этой статьи в "Кванте" — http://kvant.mccme.ru/1973/03/sobaka_bezhit_napererez.htm — и собственно, там же можно прочесть и решение Безиковича.
Victor Kleptsyn
25 October 2020
М
14:30
Математические байки
В завершение — пара кусочков из биографии Безиковича: в 1919 году (гражданская война!) он успел побывать в Пермском университете и ректором, и деканом физико-математического факультета.
Victor Kleptsyn
14:40
А в 1924 году, не получив разрешения на выезд, перешёл границу нелегально:
Victor Kleptsyn
14:49
А соседняя история про переход границы —
Victor Kleptsyn
М
16:07
Математические байки
In reply to this message
Давайте я добавлю ещё пару слов про трансляционные поверхности — про то, с чем они связаны, и пару ссылок. А именно — на них можно смотреть не только геометрически (многоугольники, стороны, параллельные переносы, склейка), но и с точки зрения комплексного анализа.
Victor Kleptsyn
М
16:34
Математические байки
А именно — очень плоская (пожалуй, термин "трансляционная" и впрямь излишне тяжеловесен) поверхность это всё равно, что пара из компактной римановой поверхности S и голоморфной 1-формы w на ней.
Если более подробно — очень плоская поверхность это почти готовое комплексное одномерное многообразие ( риманова поверхность ) : на склеиваемых многоугольниках с координатами проблем нет (они лежат на плоскости, которую можно воспринимать как R^2, а можно, как C). На рёбрах склейки тоже никаких проблем. Единственное, с чем нужно быть чуть более аккуратным, это вершины: в них зачастую собирается полный угол, больший 2π. Но за счёт того, что у нас все склейки выполняются чистыми параллельными переносами — полный угол будет всегда вида 2πk. А тогда можно перенести вершину в точку 0 в качестве локальной координаты взять корень k-й степени, который как раз уменьшит полный угол до 2π. Вот и получается комплексная структура на всей поверхности.
Если более подробно — очень плоская поверхность это почти готовое комплексное одномерное многообразие ( риманова поверхность ) : на склеиваемых многоугольниках с координатами проблем нет (они лежат на плоскости, которую можно воспринимать как R^2, а можно, как C). На рёбрах склейки тоже никаких проблем. Единственное, с чем нужно быть чуть более аккуратным, это вершины: в них зачастую собирается полный угол, больший 2π. Но за счёт того, что у нас все склейки выполняются чистыми параллельными переносами — полный угол будет всегда вида 2πk. А тогда можно перенести вершину в точку 0 в качестве локальной координаты взять корень k-й степени, который как раз уменьшит полный угол до 2π. Вот и получается комплексная структура на всей поверхности.
Victor Kleptsyn
16:35
Таблица из записок Антона Зорича — см. http://bogomolov-lab.ru/SHKOLA2013/docs/zorich.pdf
Victor Kleptsyn
16:39
In reply to this message
Так вот — комплексно-аналитическая картина для очень плоской поверхности это то, что на римановой поверхности задана голоморфная 1-форма w (которая в локальных координатах запишется как w=f(z) dz с комплексно-дифференцируемой функцией f); можно смотреть, как устроен её "неопределённый интеграл" — и наши координаты на многоугольниках это и есть её первообразная!
Victor Kleptsyn
М
17:11
Математические байки
Вот тут очень подробный (153 страницы) обзор Зорича — но 2006 года (так что там ещё нет, например, теоремы о волшебной палочке):
https://arxiv.org/pdf/math/0609392.pdf
https://arxiv.org/pdf/math/0609392.pdf
Victor Kleptsyn
17:12
А вот на этой фотографии Антон Зорич и Этьен Жис (и ещё кто-то, кого я не знаю) рассматривают собранную из прямоугольников трансляционную поверхность:
Victor Kleptsyn
17:13
Главный герой крупным планом —
Victor Kleptsyn
М
19:28
Математические байки
Ещё один объект, с которыми связаны трансляционные поверхности — это перекладывание отрезков.
А именно — берётся отрезок J, разбивается на несколько отрезков, которые после этого как-то переставляются. Получается динамическая система на J; правда, разрывная в концах подотрезков, зато сохраняющая меру Лебега. Такое отображение называется перекладыванием отрезков:
А именно — берётся отрезок J, разбивается на несколько отрезков, которые после этого как-то переставляются. Получается динамическая система на J; правда, разрывная в концах подотрезков, зато сохраняющая меру Лебега. Такое отображение называется перекладыванием отрезков:
Victor Kleptsyn
19:30
Собственно, простейший случай — перекладывание двух отрезков — уже нетривиален: это поворот окружности, просто мы эту окружность в одной точке разрезали, и смотрим на неё как на отрезок. И тут можно вспомнить все утверждения про то, что орбиты иррационального поворота плотны и распределены по мере Лебега...
Victor Kleptsyn
19:33
Так вот — на перекладывание отрезков можно смотреть как на "вертикальный" поток на правильно подобранной трансляционной поверхности (а точнее, как на отображение первого возвращения на "горизонтальную" трансверсаль) :
Victor Kleptsyn
19:34
(Картинка оттуда же: M. Viana, "Dynamics of Interval Exchange Transformations and Teichmüller Flows", http://w3.impa.br/~viana/out/ietf.pdf )
Victor Kleptsyn
М
20:06
Математические байки
In reply to this message
Ну и последнее, что я тут уже совсем парой слов хочу упомянуть, это поверхности Вича (Veech surfaces; по очевидным причинам, по-русски это название сложно гуглится).
Как мы видели, на трансляционных поверхностях действует группа SL(2,R). И иногда — как мы уже видели в случае тора, склеенного из квадрата — нетривиальные преобразования могут перевести поверхность в себя. Более того, ещё более иногда оказывается, что подгруппа G тех преобразований, которые переводят поверхность в себя (она называется группой Вича этой поверхности), оказывается очень большой — такой, что факторпространство SL(2,R)/G имеет конечный объём (тогда говорят, что G — решётка в SL(2,R)).
Например, именно так обстоит дело для поверхности, склеенной из квадрата: её стабилизатор это SL(2,Z), и эта решётка имеет конечный кообъём в SL(2,R) (при правильной нормировке получается как раз \zeta(2)=π^2/6, но это уже совсем другая история...).
Как мы видели, на трансляционных поверхностях действует группа SL(2,R). И иногда — как мы уже видели в случае тора, склеенного из квадрата — нетривиальные преобразования могут перевести поверхность в себя. Более того, ещё более иногда оказывается, что подгруппа G тех преобразований, которые переводят поверхность в себя (она называется группой Вича этой поверхности), оказывается очень большой — такой, что факторпространство SL(2,R)/G имеет конечный объём (тогда говорят, что G — решётка в SL(2,R)).
Например, именно так обстоит дело для поверхности, склеенной из квадрата: её стабилизатор это SL(2,Z), и эта решётка имеет конечный кообъём в SL(2,R) (при правильной нормировке получается как раз \zeta(2)=π^2/6, но это уже совсем другая история...).
Victor Kleptsyn
20:07
(Из книги "Математика как метафора" Ю. И. Манина, см. https://math.ru/lib/files/pdf/manin.pdf )
Victor Kleptsyn
20:17
In reply to this message
То же получается для поверхности, склеенной из конечного числа квадратиков (там стабилизатором будет подгруппа конечного индекса в SL(2,Z)). Но и не только — двойной пятиугольник, который мы видели раньше — это тоже поверхность Вича.
Victor Kleptsyn
20:20
In reply to this message
Так вот — оказывается, что на поверхности Вича параллельный поток (который мы уже видели из перекладывания отрезков) ведёт себя очень похоже на поворот окружности: в зависимости от его угла θ траектории или замыкаются, или оказываются распределены по мере Лебега. Это — дихотомия Вича (Veech Dichotomy) :
Victor Kleptsyn
20:21
Отсюда — P. Hubert, T. Schmidt, An Introduction to Veech Surfaces,
http://www.math.uchicago.edu/~masur/hs.pdf
http://www.math.uchicago.edu/~masur/hs.pdf
Victor Kleptsyn
20:29
In reply to this message
Поэтому так хорошо, что жираф на докладе Зорича был собран из одинаковых прямоугольников: значит, он является поверхностью Вича, и к потоку на нём применима теорема о дихотомии.
Victor Kleptsyn
М
20:53
Математические байки
Ну и почти последнее — из одного квадратика мы получаем "квадратный" тор. А если действовать на этот тор аффинными преобразованиями — получим торы, склеенные из всех возможных параллелограммов. Если не выделять вертикальное направление (то есть отфакторизовать по поворотам) — получится пространство торов "с геометрией" (с комплексной структурой). Это — та самая модулярная кривая (она же пространство модулей эллиптических кривых , где "модуль" = "класс эквивалентности", а "эллиптическая кривая" — синоним к "тору с комплексной структурой").
Victor Kleptsyn
20:54
Кадр из рассказа Антона Зорича на "Глобусе" (https://www.youtube.com/watch?v=oBeDuuwxk3k )
Victor Kleptsyn
21:05
In reply to this message
Именно поэтому, кстати, группу PSL(2,Z) называют ещё модулярной группой (modular group), и слова "модулярная форма" тоже относятся/восходят сюда — но это уже совсем другая история...
А если к собственно тору добавить выбор вертикального направления — и начать в вертикальном направлении сжимать, а в горизонтальном растягивать — то получится единичное касательное расслоение к модулярной кривой и геодезический поток на ней.
А если к собственно тору добавить выбор вертикального направления — и начать в вертикальном направлении сжимать, а в горизонтальном растягивать — то получится единичное касательное расслоение к модулярной кривой и геодезический поток на ней.
Victor Kleptsyn
21:10
Я надеюсь, мне удалось показать, сколько связей с разной математикой есть у трансляционных поверхностей.
Victor Kleptsyn
21:12
Ну и в завершение — прекрасная (пусть и не связанная с трансляционными поверхностями) цитата со страницы Википедии про Уильяма Вича:
Victor Kleptsyn
21:14
In reply to this message
(via https://en.wikipedia.org/wiki/William_A._Veech ; да, я проверил, и в статье по ссылке https://www.popsci.com/buckyball-magic-molecule/ из сноски она есть 🙂 )
Victor Kleptsyn
26 October 2020
М
10:40
Математические байки
Н
Непрерывное математическое образование 26.10.2020 10:39:25
«Приглашаем совершить путешествие по красивым математическим задачам. Их постановка понятна школьнику, но некоторые до сих пор не решены учёными»
Сегодня — 15 лет сайту «Математические этюды» ( https://www.etudes.ru/ ). Поздравляем коллег!
Редкий сайт живет столько времени — тем более столько времени развивается. Сегодня у Этюдов обновился сайт, видео постепенно становятся доступны в разрешении 4k; и каждую неделю во вторник на сайте будет появляться что-то новое.
Сегодня — 15 лет сайту «Математические этюды» ( https://www.etudes.ru/ ). Поздравляем коллег!
Редкий сайт живет столько времени — тем более столько времени развивается. Сегодня у Этюдов обновился сайт, видео постепенно становятся доступны в разрешении 4k; и каждую неделю во вторник на сайте будет появляться что-то новое.
Victor Kleptsyn
27 October 2020
М
11:08
Математические байки
Г
Геометрия-канал 27.10.2020 09:53:14
Три модели плоскости Лобачевского
https://etudes.ru/models/lobachevskian-plane-models/
Очень наглядное объяснение.
Сайту «Математических этюдов» вчера исполнилось 15 лет, сегодня там «Математический вторник», а значит, появилось новое видео, и это как раз оно.
https://etudes.ru/models/lobachevskian-plane-models/
Очень наглядное объяснение.
Сайту «Математических этюдов» вчера исполнилось 15 лет, сегодня там «Математический вторник», а значит, появилось новое видео, и это как раз оно.
Victor Kleptsyn
М
15:35
Математические байки
Н
Непрерывное математическое образование 27.10.2020 15:29:24
Как и было обещано, каждый вторник у Этюдов теперь премьера:
Victor Kleptsyn
М
15:35
Математические байки
М
Математические этюды 27.10.2020 15:25:30
Сегодняшний фильм — «Три модели плоскости Лобачевского» в разделе «Модели» (https://etudes.ru/models/lobachevskian-plane-models/). В фильме рассказывается, как прозрачная полусфера с нарисованными на ней окружностями, будучи освещена разными способами, может доставить три разные модели плоскости Лобачевского: модель Пуанкаре в круге, модель Кэли—Клейна на диске, модель Пуанкаре на полуплоскости.
Заметим, что Николай Иванович Лобачевский умер, не зная ни одной модели построенной теории (его книга называлась «Воображаемая геометрия»). На сегодняшний день уже известны и другие реализации, отличные от перечисленных выше.
Почему начинаем наш новый проект «Математические вторники» именно с этого фильма? О геометрии Лобачевского наслышаны все. Случайный прохожий на улице скорее всего даст неправильное «определение»: геометрия, в которой параллельные прямые пересекаются. Удивительно, что при этом в математической среде далеко не общеизвестны факты, представленные в фильме.
Напомнил про эту модель Алексей Брониславович Сосинский, опубликовав статью (https://etudes.ru/.data/localdocs/mp25_sossinsky.pdf) в сборнике «Математическое просвещение» (https://www.mccme.ru/free-books/matpros.html). Этот сборник особенно порекомендуем школьникам старших классов, увлекающимся математикой, и студентам. Это периодическое издание является переходным звеном от популярной математической литературы к профессиональной. Первая серия издавалась с 1934 по 1938, вторая — с 1957 по 1961, а третья — с 1997 года по настоящее время.
Заметим, что Николай Иванович Лобачевский умер, не зная ни одной модели построенной теории (его книга называлась «Воображаемая геометрия»). На сегодняшний день уже известны и другие реализации, отличные от перечисленных выше.
Почему начинаем наш новый проект «Математические вторники» именно с этого фильма? О геометрии Лобачевского наслышаны все. Случайный прохожий на улице скорее всего даст неправильное «определение»: геометрия, в которой параллельные прямые пересекаются. Удивительно, что при этом в математической среде далеко не общеизвестны факты, представленные в фильме.
Напомнил про эту модель Алексей Брониславович Сосинский, опубликовав статью (https://etudes.ru/.data/localdocs/mp25_sossinsky.pdf) в сборнике «Математическое просвещение» (https://www.mccme.ru/free-books/matpros.html). Этот сборник особенно порекомендуем школьникам старших классов, увлекающимся математикой, и студентам. Это периодическое издание является переходным звеном от популярной математической литературы к профессиональной. Первая серия издавалась с 1934 по 1938, вторая — с 1957 по 1961, а третья — с 1997 года по настоящее время.
Victor Kleptsyn
М
28 October 2020
М
11:29
Математические байки
In reply to this message
Итак, первое место заняла Венера (что было скорее ожидаемо, я про неё с детства помню эпитет "ближайшая"), второе — Марс. Более того, в начале опроса Марс даже лидировал:
Victor Kleptsyn
11:30
А правильный ответ удивительный — это Меркурий!
Victor Kleptsyn
М
11:47
Математические байки
Давайте посмотрим, почему это так и как это можно прикинуть. Во-первых — сразу исключим Юпитер. Перигелий Юпитера — 4.9 астрономических единицы (а.е. = большая полуось орбиты Земли, т.е. "радиус", если пренебречь небольшим, всего в полтора процента, эксцентриситетом орбиты Земли). Конечно, то, что это 4.9, я аккуратно подсмотрел, но "около 5" вполне помнилось.
Так вот — если Юпитер не бывает к Солнцу ближе 4.9 а.е., то просто по неравенству треугольника он к Земле не бывает ближе 3.9 а.е. — и потому ни секунды не был к Земле ближе, чем Меркурий или Венера (которые не могут быть дальше 2а.е.), и даже чем Марс (афелий которого это 1.6 а.е., так что максимальное удаление от Земли 2.6 а.е.).
Так что Юпитер исключаем сразу.
Так вот — если Юпитер не бывает к Солнцу ближе 4.9 а.е., то просто по неравенству треугольника он к Земле не бывает ближе 3.9 а.е. — и потому ни секунды не был к Земле ближе, чем Меркурий или Венера (которые не могут быть дальше 2а.е.), и даже чем Марс (афелий которого это 1.6 а.е., так что максимальное удаление от Земли 2.6 а.е.).
Так что Юпитер исключаем сразу.
Victor Kleptsyn
11:53
Давайте я перепишу сюда данные по трём оставшимся планетам — сначала полностью, а потом мы их "огрубим" до уровня "для первой прикидки сойдёт":
Меркурий: перигелий 0.307 AU, афелий 0.466 AU;
большая полуось 0.387 AU, эксцентриситет 0.20
Венера: перигелий 0.718 AU, афелий 0.728 AU;
большая полуось 0.723 AU, эксцентриситет 0.0067
Марс: перигелий 1.382 AU, афелий 1.666 AU;
большая полуось 1.523 AU, эксцентриситет 0.09
Земля: перигелий 0.983 AU, афелий 1.016 AU;
большая полуось 1 AU (по определению!), эксцентриситет 0.016
Меркурий: перигелий 0.307 AU, афелий 0.466 AU;
большая полуось 0.387 AU, эксцентриситет 0.20
Венера: перигелий 0.718 AU, афелий 0.728 AU;
большая полуось 0.723 AU, эксцентриситет 0.0067
Марс: перигелий 1.382 AU, афелий 1.666 AU;
большая полуось 1.523 AU, эксцентриситет 0.09
Земля: перигелий 0.983 AU, афелий 1.016 AU;
большая полуось 1 AU (по определению!), эксцентриситет 0.016
Victor Kleptsyn
12:01
Видно, что у Меркурия эксцентриситет совсем немаленький (разница между наименьшим и наибольшим расстоянием в полтора раза!), да и у Марса вполне заметный. Но давайте для первой прикидки сделаем картинку, считая все орбиты просто круговыми (и взяв за радиусы большие полуоси). Кстати — вот полуоси с одним знаком после запятой, 0.4 (округляя вверх), 0.7 и 1.5 — совершенно без проблем запоминаются (а для прикидки больше и не надо).
(И расстояние в а.е. гораздо проще помнить, чем в миллионах километров!)
(И расстояние в а.е. гораздо проще помнить, чем в миллионах километров!)
Victor Kleptsyn
12:10
Отсюда уже видно, в чём проблема у Марса — когда он подходит близко к Земле, он действительно к ней довольно близко (ближе может быть только Венера) — но только при большей части взаимных расположений он от Земли будет далеко!
Victor Kleptsyn
М
12:28
Математические байки
Кстати — это хороший момент, чтобы вопрос переформулировать. А именно — давайте поверим, что у наших планет нет заметных орбитальных резонансов, что периоды их обращения вокруг Солнца рационально-независимы. Тогда за большое время планеты окажутся "во всех возможных расположениях", и усреднение по времени (от какой-нибудь величины) будет давать такой же результат, как независимое усреднение по всем планетам, для каждой — за её период.
Иными словами, если мы возьмём тор (четырёхмерный, ибо у нас 4 планеты, Меркурий, Венера, Земля, Марса), координаты на котором это 4 "времени года" (фазы, положения на орбите) этих планет — то за большое время траектория окажется распределена почти в соответствии с мерой Лебега на этом торе. И это называется "эргодичность иррационального потока на торе".
(Ну, дальше есть тонкий вопрос, а что такое "достаточно большое время", но это я замету под ковёр, просто сказав, что пока прикидываем так, и что прикидка таки работает.)
Иными словами, если мы возьмём тор (четырёхмерный, ибо у нас 4 планеты, Меркурий, Венера, Земля, Марса), координаты на котором это 4 "времени года" (фазы, положения на орбите) этих планет — то за большое время траектория окажется распределена почти в соответствии с мерой Лебега на этом торе. И это называется "эргодичность иррационального потока на торе".
(Ну, дальше есть тонкий вопрос, а что такое "достаточно большое время", но это я замету под ковёр, просто сказав, что пока прикидываем так, и что прикидка таки работает.)
Victor Kleptsyn
12:40
Посмотрим на Марс и убедимся, что он в этом "круговом" приближении даже только у Меркурия не может выиграть чаще, чем в трети случаев. Вот три картинки — Меркурий в максимально удалённой от Земли точке, "под 90 градусов" и в максимально близкой точке:
Victor Kleptsyn
12:41
In reply to this message
Даже когда Меркурий "даёт Марсу фору", оказываясь максимально далеко — и то Марс оказывается ближе к Земле лишь чуть больше трети времени.
Victor Kleptsyn
12:42
Когда Меркурий "под 90 градусов" — Марсу остаётся уже немного меньше трети.
Victor Kleptsyn
12:43
Когда Меркурий близко к Земле — поражение Марса почти неминуемо, ему остаётся меньше десятой доли времени. И это всё ещё без учёта Венеры — которая тоже возьмёт свою долю (особенно в "удобных" условиях, когда Меркурий "отошёл подальше").
Victor Kleptsyn
12:47
In reply to this message
Я тут, конечно, сильно сжульничал, пустив Меркурий по круговой орбите радиуса 0.4, вместо заметно эллиптической. Но тут можно сказать, что в зависимости от положения Земли эллиптичность может сыграть Меркурию как в минус (если он окажется дальше), так и в плюс (если он окажется ближе). И в первом приближении это должно повлиять не очень сильно.
Victor Kleptsyn
12:49
А раз победитель (из трёх кандидатов) должен быть ближайшим больше трети времени — то Марс не может выиграть. Остаётся решить, кто выигрывает — Меркурий или Венера.
Victor Kleptsyn
12:49
И если бы мы сравнивали друг с другом только их — то победа Меркурия (даже с учётом эллиптичности его орбиты) получалась бы рассуждением классической геометрии 🙂
Victor Kleptsyn
12:52
Потому что — для каждого положения Меркурия посмотрим, какую долю времени выигрывает у него Венера, когда Земля находится где-нибудь — и когда она на диаметрально противоположной точке своей орбиты:
Victor Kleptsyn
12:59
Каждой из этих долей соответствуют точки орбиты Венеры внутри соответствующих окружностей с центром в одном из положений Земли. Но внутренности этих окружностей пересекаются только внутри орбиты Венеры — а значит, высекаемые ими кусочки орбиты Венеры не пересекаются. И поэтому полусумма долей, когда Венера выигрывает у Меркурия при одном и при другом положении Земли, меньше половины. Усредняя — получаем, что Венера у Меркурия выигрывает меньше половины времени, так что в "зачёте матчей один на один" Меркурий точно выигрывает. (И это рассуждение вполне универсальное.)
Victor Kleptsyn
13:07
Увы, дальше начинает работать парадокс голосования: может быть, Марс, который не может выиграть — оттянет на себя "голоса" (простите, долю времени) у Меркурия, и из-за этого выиграет Венера.
Более того, можно построить "искусственный пример" (чисто математический, конечно), когда все орбиты круговые, с независимыми периодами — но выигрывает не самая внутренняя планета!
Более того, можно построить "искусственный пример" (чисто математический, конечно), когда все орбиты круговые, с независимыми периодами — но выигрывает не самая внутренняя планета!
Victor Kleptsyn
13:15
А именно — представим себе, что вместо одной Венеры по близким орбитам их крутится пара-тройка десятков (кто сказал "пояс астероидов"?), с немного отличающимися периодами. Тогда, чтобы Меркурий выиграл, нужно как минимум, чтобы на дуге через ближайшую точку его орбиты не было ни одной Венеры:
Victor Kleptsyn
13:16
А вероятность этого экспоненциально мала (по количеству N Венер). Так что, начиная с определённого их количества, она становится меньше 1/(N+1) — и выиграет одна из N Венер.
Victor Kleptsyn
13:21
Кстати, можно прикинуть, сколько их для этого нужно. Дуга размера 72 градуса это (1/5) от длины окружности, так что нам нужно, чтобы выполнялось
(4/5)^N < 1/(N+1).
(4/5)^10 это чуть больше 0.1, а вот (4/5)^12 уже 0.068<0.7<1/13.
(4/5)^N < 1/(N+1).
(4/5)^10 это чуть больше 0.1, а вот (4/5)^12 уже 0.068<0.7<1/13.
Victor Kleptsyn
13:22
(Но это если орбиту внутренней планеты взять круговой радиуса 0.4)
Victor Kleptsyn
13:25
Впрочем, несмотря на всё вышесказанное, для нашей тройки Меркурий-Венера-Марс, выигрывает таки Меркурий, примерно с соотношением 0.46:0.36:0.18.
Victor Kleptsyn
13:28
Ну и 0.46 можно, опять-таки, прикинуть — посмотрев на полусумму долей времени выигрыша Меркурия, по двум противоположным положениям Земли. Когда Меркурий с Землёй на одной прямой через Солнце, то в ближайшем положении он довольно сильно выигрывает, в наиболее удалённом больше всего проигрывает, но даже так среднее арифметическое даёт 0.49:
Victor Kleptsyn
13:28
А в положении "под 90" получается 0.43:
Victor Kleptsyn
13:28
Ну и среднее арифметическое как раз 0.46.
Victor Kleptsyn
13:41
Это, конечно, "прикидка на коленке". Но она оказывается вполне точной: вот видео с честной симуляцией
https://www.youtube.com/watch?v=GDgbVIqGADQ
(собственно, откуда я эту историю и узнал, точнее, из его адаптации —
https://www.youtube.com/watch?v=SumDHcnCRuU )
https://www.youtube.com/watch?v=GDgbVIqGADQ
(собственно, откуда я эту историю и узнал, точнее, из его адаптации —
https://www.youtube.com/watch?v=SumDHcnCRuU )
Victor Kleptsyn
М
13:59
Математические байки
И последнее: если вместо вопроса про долю времени мы будем спрашивать, "какая планета в среднем ближайшая", то в приближении круговых орбит угадать, что опять победит Меркурий, довольно несложно.
Представьте себе график расстояния до Земли. Это верхняя половина конуса с вершиной в Земле. В частности — это выпуклая функция. Поэтому её среднее по кругам-орбитам с центром в Солнце будет возрастать с радиусом. Ибо — проводим касательную к внутренней окружности до пересечений BC с внешней и пользуемся неравенством Йенсена (в данном случае — неравенством треугольника, что расстояние до точки касания меньше среднего арифметического расстояний до концов дуги BC), после чего усредняем по положению внутренней планеты:
Представьте себе график расстояния до Земли. Это верхняя половина конуса с вершиной в Земле. В частности — это выпуклая функция. Поэтому её среднее по кругам-орбитам с центром в Солнце будет возрастать с радиусом. Ибо — проводим касательную к внутренней окружности до пересечений BC с внешней и пользуемся неравенством Йенсена (в данном случае — неравенством треугольника, что расстояние до точки касания меньше среднего арифметического расстояний до концов дуги BC), после чего усредняем по положению внутренней планеты:
Victor Kleptsyn
М
14:27
Математические байки
In reply to this message
На самом деле — тут по делу даже не выпуклость, а (следующая из неё) положительность оператора Лапласа (а Δ(r)>0 можно увидеть и непосредственно). И тут надо вспомнить про гармонические функции: Δ(f)=0 (для "хороших" f) равносильно тому, что среднее f по окружности с данным центром это просто её значение в центре (собственно, в одну сторону это так и называется, "теорема о среднем значении для гармонических функций"). Ну и давайте я тут вспомню летнюю лекцию Александра Логунова.
Victor Kleptsyn
29 October 2020
М
13:10
Математические байки
Н
Непрерывное математическое образование 29.10.2020 12:40:21
недавно было 80 лет со дня рождения Николая Борисовича Васильева — в новый Квант (№8 за 2020 год) вошел текст о нем, его статья, поборка задач
Victor Kleptsyn
М
17:51
Математические байки
In reply to this message
Анекдот в тему — как специалист по теории вероятностей проверяет, что интеграл от 0 до 1 от x^N это 1/(N+1)?
Он выбирает на отрезке [0,1] равномерно и независимо N+1 точку и спрашивает, с какой вероятностью первая из них правее всего? С одной стороны, вероятность этого 1/(N+1), с другой, это интеграл от x^N (вероятность того, что все остальные меньше её, если она приняла значение x) по dx (распределение значений = мера Лебега).
Он выбирает на отрезке [0,1] равномерно и независимо N+1 точку и спрашивает, с какой вероятностью первая из них правее всего? С одной стороны, вероятность этого 1/(N+1), с другой, это интеграл от x^N (вероятность того, что все остальные меньше её, если она приняла значение x) по dx (распределение значений = мера Лебега).
Victor Kleptsyn
М
18:29
Математические байки
А геометрически можно сказать, что куб [0,1]^{N+1} нарезается на N+1 равную (но неправильную!) пирамиду с основанием [0,1]^N (и общей вершиной (1,1,...,1) ) — по тому, какая координата наибольшая.
Кстати, точно так же куб [0,1]^n можно разрезать на n! одинаковых (неправильных — зато "довольно прямоугольных") симплекса — по тому, в каком порядке идут координаты. И тут можно сказать про группу перестановок координат, порождённую их транспозициями = отражениями относительно плоскостей x_i=x_j, и её фундаментальную область... Или сказать слова "группа Вейля" и "камера Вейля" ( https://ru.wikipedia.org/wiki/Группа_Вейля ).
Или спросить — "Самурай разрубил куб [0,1]^3 вдоль плоскостей x=y, y=z и z=x. Сколько и каких частей получилось?".
Или вспомнить про классификацию правильных многогранников — группы симметрий которых порождаются отражениями (и я тут хочу вспомнить брошюру Е. Смирнова, https://www.mccme.ru/free-books/dubna/smirnov-reflections-v2.pdf — и соответствующую картинку из неё)
Кстати, точно так же куб [0,1]^n можно разрезать на n! одинаковых (неправильных — зато "довольно прямоугольных") симплекса — по тому, в каком порядке идут координаты. И тут можно сказать про группу перестановок координат, порождённую их транспозициями = отражениями относительно плоскостей x_i=x_j, и её фундаментальную область... Или сказать слова "группа Вейля" и "камера Вейля" ( https://ru.wikipedia.org/wiki/Группа_Вейля ).
Или спросить — "Самурай разрубил куб [0,1]^3 вдоль плоскостей x=y, y=z и z=x. Сколько и каких частей получилось?".
Или вспомнить про классификацию правильных многогранников — группы симметрий которых порождаются отражениями (и я тут хочу вспомнить брошюру Е. Смирнова, https://www.mccme.ru/free-books/dubna/smirnov-reflections-v2.pdf — и соответствующую картинку из неё)
Victor Kleptsyn
30 October 2020
М
13:14
Математические байки
Коллеги пишут, что задача про разрезание куба на три пирамиды была на Московской математической олимпиаде в 1953-м: см. https://problems.ru/view_by_source_new.php?parent=168097 (это вариант 9-го класса, но она была и в 10-м). Не знал! 🙂
Victor Kleptsyn
М
13:15
Математические байки
Н
Непрерывное математическое образование 30.10.2020 09:22:23
Дальше в матбайках обсуждается геометрическая версия этого рассуждения. Если отложить пока в сторону умные разговоры про группу Вейля и т.п., то речь идет просто о том, что например,
куб можно разрезать на 3 равные пирамиды с квадратным основанием
— такая задача, кстати, предлагалась на Московской математической олимпиаде в 1953 году.
куб можно разрезать на 3 равные пирамиды с квадратным основанием
— такая задача, кстати, предлагалась на Московской математической олимпиаде в 1953 году.
Victor Kleptsyn
М
13:19
Математические байки
А вот ещё "ответное слово" — вероятностное доказательство для суммы обратных квадратов:
Victor Kleptsyn
М
13:19
Математические байки
q
qtasep 30.10.2020 06:12:50
А вот ещё и «вероятностное» доказательство pi^2/6, отсюда https://www.tandfonline.com/doi/abs/10.4169/amer.math.monthly.118.07.641
Victor Kleptsyn
М
13:20
Математические байки
Очень красиво, и этого я тоже не знал!
Victor Kleptsyn
13:23
(Интересно, есть ли у этого какое-то красивое объяснение — почему нужно брать именно распределения Коши?)
Victor Kleptsyn
4 November 2020
М
10:33
Математические байки
М
Математические этюды 03.11.2020 10:03:24
В старших классах школы изучаются гиперболы и параболы, но мало кто в школе знает, что такое гиперболический параболоид, ведь этот объект — предмет изучения студентов. Тем не менее, картонную модель гиперболического параболоида (https://etudes.ru/models/conic-sections-hyperbolic-paraboloid-carboard-model/) можно сделать и обсудить даже с детьми!
Увидеть анимированное определение гиперболического параболоида, разобраться, где там параболы, а где гиперболы, можно на нашем сайте по ссылке https://etudes.ru/models/conic-sections-sadle-hyperbolic-paraboloid/. Чипсам, упакованным в цилиндрические тубусы, чтобы они меньше крошились, придают форму как раз гиперболического параболоида. Это одно из интересных и простых применений такой поверхности в обычной жизни. Проведя сильно противоречащий интуиции эксперимент с чипсами, представленный у нас на сайте в ролике «Чипсы: гиперболический параболоид» (https://etudes.ru/models/conic-sections-crisps-hyperbolic-paraboloid/), можно убедиться, что гиперболический параболоид — линейчатая поверхность. Кстати, оба ролика теперь доступны в разрешении 4k!
Конкурс этой недели, в рамках которого мы разыгрываем книгу «Математическая составляющая», связан с картонной моделью гиперболического параболоида и будет интересен как детям, так и взрослым (ссылка на конкурс). Сделанная модель наглядно иллюстрирует свойство линейчатости. Также, используя модель, можно увидеть ещё один интересный факт: если попытаться изогнуть лист бумаги без разрезов в форме гиперболического параболоида, то ничего не выйдет — в каком-нибудь месте бумага обязательно будет отстоять от поверхности. Искушённый читатель правильно скажет, что у гиперболического параболоида отрицательная кривизна. Попробуйте наложить на сделанную модель лист бумаги и убедиться в этом.
Посмотреть на картонную модель гиперболического параболоида можно, например, в журнале «Квант» (№3 за 1990 год). Напомним, что архив всех номеров журнала можно найти на сайте https://kvant.ras.ru/. Кстати в этом году, Кванту исполнилось 50 лет!
Когда-то, в Древней Индии математическим доказательством считалась картинка иллюстрирующая математический факт, сопровождаемая надписью «Смотри!». Вот и мы в этот раз, давая лишь картинку, идём по этому пути. Sapienti sat. Только в данном случае лучше перефразировать – не «умному», а «желающему».
Увидеть анимированное определение гиперболического параболоида, разобраться, где там параболы, а где гиперболы, можно на нашем сайте по ссылке https://etudes.ru/models/conic-sections-sadle-hyperbolic-paraboloid/. Чипсам, упакованным в цилиндрические тубусы, чтобы они меньше крошились, придают форму как раз гиперболического параболоида. Это одно из интересных и простых применений такой поверхности в обычной жизни. Проведя сильно противоречащий интуиции эксперимент с чипсами, представленный у нас на сайте в ролике «Чипсы: гиперболический параболоид» (https://etudes.ru/models/conic-sections-crisps-hyperbolic-paraboloid/), можно убедиться, что гиперболический параболоид — линейчатая поверхность. Кстати, оба ролика теперь доступны в разрешении 4k!
Конкурс этой недели, в рамках которого мы разыгрываем книгу «Математическая составляющая», связан с картонной моделью гиперболического параболоида и будет интересен как детям, так и взрослым (ссылка на конкурс). Сделанная модель наглядно иллюстрирует свойство линейчатости. Также, используя модель, можно увидеть ещё один интересный факт: если попытаться изогнуть лист бумаги без разрезов в форме гиперболического параболоида, то ничего не выйдет — в каком-нибудь месте бумага обязательно будет отстоять от поверхности. Искушённый читатель правильно скажет, что у гиперболического параболоида отрицательная кривизна. Попробуйте наложить на сделанную модель лист бумаги и убедиться в этом.
Посмотреть на картонную модель гиперболического параболоида можно, например, в журнале «Квант» (№3 за 1990 год). Напомним, что архив всех номеров журнала можно найти на сайте https://kvant.ras.ru/. Кстати в этом году, Кванту исполнилось 50 лет!
Когда-то, в Древней Индии математическим доказательством считалась картинка иллюстрирующая математический факт, сопровождаемая надписью «Смотри!». Вот и мы в этот раз, давая лишь картинку, идём по этому пути. Sapienti sat. Только в данном случае лучше перефразировать – не «умному», а «желающему».
Victor Kleptsyn
М
10:38
Математические байки
In reply to this message
Мне тут больше всего нравится (не попавшая в пересказ) изгибаемость:
Victor Kleptsyn
10:39
Victor Kleptsyn
10:42
И сначала это кажется чем-то совершенно мистическим ("существует семейство деформаций параболоидов, сохраняющих оба семейства образующих и изометричных на каждом из них"), пока не догадаешься посмотреть на это сверху — или, что то же самое, спроецировать вдоль направления, по которому оранжевые и фиолетовые плоскости пересекаются, на горизонтальную плоскость.
Victor Kleptsyn
10:43
А тогда наша конструкция становится просто решёткой из параллелограммов, которая "складывается" самым, что ни на есть, естественным образом.
Victor Kleptsyn
10:53
А ещё — оказывается, Этюды ещё в феврале выложили текст/модель про появление конических сечений в муарах:
https://etudes.ru/models/conic-sections-moire/
https://etudes.ru/models/conic-sections-moire/
Victor Kleptsyn
М
11:37
Математические байки
Ну и мне это напомнило муаровую картинку, которую мне когда-то показал совершенно замечательный Тадаси Токиэда (Tadashi Tokieda). А именно — возьмём две шахматных решётки, одна из которых напечатана (или нарисована) на прозрачной бумаге:
Victor Kleptsyn
11:38
А теперь давайте их наложим одну на другую — и будем поворачивать. Что получится? Оказывается, получается очень красивая картина:
Victor Kleptsyn
11:43
А ещё интереснее, если исходная решётка была треугольной... Попробуйте сделать сами (когда Тадаси мне это показал, я прыгал от восторга)! Ну а когда я рассказал это Коле Андрееву, он сказал, что уже знает по другой причине — см. последнюю иллюстрацию отсюда: https://book.etudes.ru/toc/colorspaces/#xtra1
Victor Kleptsyn
11:46
А ещё можно вспомнить двуслойный графен — и то, что происходит с его слоями при повороте: вот тут ( https://elementy.ru/problems/835/Uzory_dvukhsloynogo_grafena ) задача Игоря Иванова, а вот тут ( https://nplus1.ru/news/2018/03/05/magic-graphene ) — новость про его превращение в сверхпроводник при правильном выборе угла
Victor Kleptsyn
8 November 2020
М
21:12
Математические байки
К вечеру воскресенья — давайте я поделюсь несколькими видео:
1) Савватеев про задачу про сборку замкнутой дороги. Очень хорошо сделано — и задача действительно удачно выбрана. Когда он предлагает поставить паузу и подумать — это и впрямь стоит сделать!
https://www.youtube.com/watch?v=lLZzgpG5320
2) Очень классно сделанное видео про клеточные автоматы — https://www.youtube.com/watch?v=FiO6jkNkrb4 (мои поздравления автору!). Тут не только игра "Жизнь", но и ракушка и "правило 30 Вольфрама", и муравей Лэнгтона (а под конец — и его 3d-аналог), и заканчивается, действительно, [некоторой] 3d-версией игры "Жизнь" — похожим на неё клеточным автоматом с "достаточно интересным" поведением.
3) свежее видео Numberphile с практически "пляшущими человечками":
https://www.youtube.com/watch?v=9p55Qgt7Ciw
1) Савватеев про задачу про сборку замкнутой дороги. Очень хорошо сделано — и задача действительно удачно выбрана. Когда он предлагает поставить паузу и подумать — это и впрямь стоит сделать!
https://www.youtube.com/watch?v=lLZzgpG5320
2) Очень классно сделанное видео про клеточные автоматы — https://www.youtube.com/watch?v=FiO6jkNkrb4 (мои поздравления автору!). Тут не только игра "Жизнь", но и ракушка и "правило 30 Вольфрама", и муравей Лэнгтона (а под конец — и его 3d-аналог), и заканчивается, действительно, [некоторой] 3d-версией игры "Жизнь" — похожим на неё клеточным автоматом с "достаточно интересным" поведением.
3) свежее видео Numberphile с практически "пляшущими человечками":
https://www.youtube.com/watch?v=9p55Qgt7Ciw
Victor Kleptsyn
21:13
(Но до и после там тоже интересно!)
Victor Kleptsyn
10 November 2020
М
11:28
Математические байки
О, какая прекрасная история!
Victor Kleptsyn
М
11:28
Математические байки
K
Khavr History 09.11.2020 15:14:50
Краткая иллюстрация того, как расшифровывают знаки, обозначающие цифры в умерших языках.
https://katherinemcdonald.net/2020/11/05/the-mystery-of-etruscan-4-and-6/
https://katherinemcdonald.net/2020/11/05/the-mystery-of-etruscan-4-and-6/
Victor Kleptsyn
М
14:04
Математические байки
М
Математические этюды 10.11.2020 10:01:41
Премьера сайта «Математические этюды».
А вы знаете, как изобразить эллипс, обладая лишь карандашом, замкнутой ниткой и двумя гвоздями? Надо накинуть нить на два вбитых гвоздя. Тогда кривая, которую нарисует карандаш, если в каждый момент он будет натягивать нить, как раз и будет эллипсом, а гвоздики будут находиться в его фокусах. Часто математики именно так и определяют: эллипс — геометрическое место точек, сумма расстояний от которых до двух выделенных точек (фокусов) постоянна.
А что будет, если на плоскость положить уже готовый эллипс из плотного материала и использовать его вместо гвоздей? Оказывается, карандаш, натягивающий нить, опять нарисует эллипс, причём софокусный исходному. Это утверждение называется теоремой Грейвза и именно о ней сегодняшний наш фильм https://etudes.ru/models/conic-sections-confocal-ellipses/.
А вы знаете, как изобразить эллипс, обладая лишь карандашом, замкнутой ниткой и двумя гвоздями? Надо накинуть нить на два вбитых гвоздя. Тогда кривая, которую нарисует карандаш, если в каждый момент он будет натягивать нить, как раз и будет эллипсом, а гвоздики будут находиться в его фокусах. Часто математики именно так и определяют: эллипс — геометрическое место точек, сумма расстояний от которых до двух выделенных точек (фокусов) постоянна.
А что будет, если на плоскость положить уже готовый эллипс из плотного материала и использовать его вместо гвоздей? Оказывается, карандаш, натягивающий нить, опять нарисует эллипс, причём софокусный исходному. Это утверждение называется теоремой Грейвза и именно о ней сегодняшний наш фильм https://etudes.ru/models/conic-sections-confocal-ellipses/.
Victor Kleptsyn
М
14:07
Математические байки
In reply to this message
Я помню, какой удивительной мне показалась эта теорема, когда я её в первый раз услышал — как раз из-за того, что я знал, что длина дуги эллипса задаётся интегралом, который в элементарных функциях не выражается.
Victor Kleptsyn
11 November 2020
М
11:18
Математические байки
In reply to this message
Физическое доказательство, которое там упоминается, на самом деле, очень естественное. А именно — если вокруг любой выпуклой фигуры прорисовывать кривую "по Грейвсу", то касательная к ней будет перпендикуляром к биссектрисе угла, образованного двух отрезками, отходящими от карандаша.
Потому что на карандаш действует сила "реакции нитки", складывающаяся из двух сил, приходящих из двух отрезков. Но в отсутствие трения натяжение нити на всём её протяжении одинаково по модулю — так что мы складываем два равных по модулю вектора. И их равнодействующая будет направлена по биссектрисе угла между двумя отрезками — а, соответственно, карандаш будет двигаться перпендикулярно этому направлению:
Потому что на карандаш действует сила "реакции нитки", складывающаяся из двух сил, приходящих из двух отрезков. Но в отсутствие трения натяжение нити на всём её протяжении одинаково по модулю — так что мы складываем два равных по модулю вектора. И их равнодействующая будет направлена по биссектрисе угла между двумя отрезками — а, соответственно, карандаш будет двигаться перпендикулярно этому направлению:
Victor Kleptsyn
11:25
С другой стороны, мы знаем про оптическое свойство эллипса — что касательная к нему тоже перпендикулярна биссектрисе, только другого угла: угла, образуемого отрезками, соединяющими точку с фокусами. (Собственно, можно сказать, что это вырожденный случай предыдущего, когда фигуру заменили на отрезок от одного фокуса до другого.)
Victor Kleptsyn
11:26
Значит, нужно проверить равенство двух углов между касательными из внешней точки к эллипсу и направлениями на фокусы:
Victor Kleptsyn
11:27
А это уже простой геометрический факт: если отразить отрезки из фокусов в точки касания относительно касательных, то появятся два равных по трём сторонам треугольника:
Victor Kleptsyn
М
12:36
Математические байки
In reply to this message
Да, физическое рассуждение тут можно заменить на вот какое: если зафиксировать на дальней дуге эллипса некоторую точку, то полная длина нитки это длина пути "отрезок+дуга" с одной и с другой стороны. А если посмотреть на градиент одного из двух слагаемых, то это как раз и будет единичный вектор, направленный по соответствующему отрезку (правда, в направлении от точки касания, потому что градиент, а не минус градиент). Ну и градиентом суммы будет сумма градиентов — как раз вектор, направленный по биссектрисе (но наружу). А линия уровня перпендикулярна градиенту.
Victor Kleptsyn
М
13:37
Математические байки
А линия уровня для одной такой суммы называется эвольвентой (рис.: https://commons.wikimedia.org/wiki/File:Evolvente-parabel.svg#/media/File:Evolvente-parabel.svg ) ; что совершенно естественно, центром кривизны эвольвенты в какой-нибудь точке является точка касания нитки с исходной кривой в соответствующий момент: мгновенным образом нитка "крутится" именно вокруг неё. Поэтому (локально) обратная операция к построению эвольвенты это взятие множества центров кривизны — которое называется эволютой .
Victor Kleptsyn
13:44
In reply to this message
И именно с этим связано то, что соприкасающиеся окружности на отрезке кривой, где радиус кривизны меняется монотонно, оказываются вложены друг в друга. Потому что если рассмотреть кривую Г как эвольвенту её кривой центров Г', то изменение радиуса кривизны это длина соответствующей дуги кривой Г' ("на сколько размоталась верёвка"), а само смещение центра это хорда этой дуги. Поэтому расстояние между центрами соприкасающихся окружностей меньше разности их радиусов — и вот и вложенность!
Victor Kleptsyn
12 November 2020
М
18:04
Математические байки
Н
Непрерывное математическое образование 10.11.2020 14:31:12
Владимир Федорович Овчинников (04.10.1928–10.11.2020)
легендарный директор Второй школы (с основания и до 1971 г. и в 2001–2020 гг.)
легендарный директор Второй школы (с основания и до 1971 г. и в 2001–2020 гг.)
Victor Kleptsyn
18:04
Н
Непрерывное математическое образование 11.11.2020 10:12:00
https://t.me/cme_channel/478
напомним про материалы Второй школы 60-х годов
и на списки преподавателей интересно, да, посмотреть — напр., https://www.mathedu.ru/text/matshkola_lektsii_i_zadachi_v1_1965/p43/
напомним про материалы Второй школы 60-х годов
и на списки преподавателей интересно, да, посмотреть — напр., https://www.mathedu.ru/text/matshkola_lektsii_i_zadachi_v1_1965/p43/
Victor Kleptsyn
14 November 2020
М
13:50
Математические байки
Давайте я ещё чуть-чуть порекламирую Этюды: вот тут ( https://etudes.ru/sketches/ellipse-envelope/ ) анимация, в которой эллипс появляется как огибающая. А именно — если взять окружность, по которой бегает точка P, и точку A внутри неё — то огибающая перпендикуляров к AP в точке P будет эллипсом, касающимся этой окружности и с A как одним из фокусов:
Victor Kleptsyn
13:52
Правда, мне это утверждение чуть больше нравится в варианте, получаемом сжатием в два раза: огибающая серединных перпендикуляров к отрезку AP это эллипс, фокусы которого это A и центр окружности.
Victor Kleptsyn
14:02
И в таком виде на это проще всего смотреть в обратную сторону — взять такой эллипс, провести касательную к нему в какой-то точке Q, и отразить отрезок AQ относительно неё. Получающийся отрезок PQ попадает на продолжение отрезка BQ (ибо свойство эллипса), а значит, расстояние BP как раз равно сумме расстояний до фокусов:
BP=QA+QB=const
Поэтому точка P бегает как раз по окружности с центром во втором фокусе B (а радиус этой окружности — длина нити, использованной при построении эллипса).
BP=QA+QB=const
Поэтому точка P бегает как раз по окружности с центром во втором фокусе B (а радиус этой окружности — длина нити, использованной при построении эллипса).
Victor Kleptsyn
14:08
А ещё это утверждение связано с эллиптичностью орбит. И давайте я тут процитирую коллег:
Victor Kleptsyn
М
14:09
Математические байки
Н
Непрерывное математическое образование 13.01.2018 19:49:20
появление эллипса на круглом листе бумаги ( via vk.com/thebeautyoftruth )
Victor Kleptsyn
М
14:09
Математические байки
Н
Непрерывное математическое образование 03.08.2018 13:23:53
к картинке про эллипс выше
1) слайды про оптическое свойство и прочее
2) видео https://youtu.be/xdIjYBtnvZU про то, как такая геометрия связана с эллиптичностью орбит планет
1) слайды про оптическое свойство и прочее
2) видео https://youtu.be/xdIjYBtnvZU про то, как такая геометрия связана с эллиптичностью орбит планет
Victor Kleptsyn
М
14:14
Математические байки
И чуть-чуть перескажу это видео своими словами — но его стоит посмотреть целиком, оно очень хорошо сделано.
Основной шаг (который очень хорошо запоминается!) там такой: давайте отложим от начала координат вектора скоростей планеты в разные моменты времени.
Теорема: это окружность — правда, с центром не в начале координат.
(Ещё можно сказать, "годограф скоростей круглый")
Основной шаг (который очень хорошо запоминается!) там такой: давайте отложим от начала координат вектора скоростей планеты в разные моменты времени.
Теорема: это окружность — правда, с центром не в начале координат.
(Ещё можно сказать, "годограф скоростей круглый")
Victor Kleptsyn
14:25
In reply to this message
Доказательство: запараметризуем орбиту вместо времени углом из Солнца. Производная скорости по углу будет направлена по радиус-вектору — и будет пропорционально произведению силы притяжения на время на прохождение заданного угла (ну то есть обратно пропорционально угловой скорости).
* Сила притяжения обратно пропорциональна квадрату расстояния, ибо закон всемирного тяготения;
* Время на прохождение угла прямо пропорционально квадрату расстояния, ибо второй закон Кеплера a.k.a. закон сохранения момента импульса (площадь равнобедренного треугольника с фиксированным углом при вершине пропорционален квадрату его боковой стороны).
И вот квадрат расстояния сокращается — и в такой параметризации производная по углу (жёлтый вектор на рисунке выше) постоянна по модулю. Интегрируя — как раз и получаем, что конец вектора скорости ходит по окружности, правда, с центром где угодно (ибо "плюс константа").
* Сила притяжения обратно пропорциональна квадрату расстояния, ибо закон всемирного тяготения;
* Время на прохождение угла прямо пропорционально квадрату расстояния, ибо второй закон Кеплера a.k.a. закон сохранения момента импульса (площадь равнобедренного треугольника с фиксированным углом при вершине пропорционален квадрату его боковой стороны).
И вот квадрат расстояния сокращается — и в такой параметризации производная по углу (жёлтый вектор на рисунке выше) постоянна по модулю. Интегрируя — как раз и получаем, что конец вектора скорости ходит по окружности, правда, с центром где угодно (ибо "плюс константа").
Victor Kleptsyn
14:36
In reply to this message
Этого ещё не хватает — нужно добавить, что по этой окружности в этой параметризации (по углу из Солнца) конец вектора скорости движется равномерно (что мы, собственно, рассуждением выше тоже доказали), и использовать это, чтобы вернуться обратно и построить орбиту.
Victor Kleptsyn
14:40
И если развернуть картинку скоростей на 90 градусов, а потом нарисовать [серединные] перпендикуляры ("разворачивая скорости обратно") — то как раз нужная картинка и образуется:
Victor Kleptsyn
14:48
In reply to this message
Вот. А ещё — если точка A была снаружи окружности, то огибающая получается гиперболой (что, естественно, соответствует гиперболическим орбитам) — https://etudes.ru/sketches/hyperbola-envelope/ .
И получающаяся картинка мне очень напоминает однополостный гиперболоид с одним из двух семейств прямых на нём.
И получающаяся картинка мне очень напоминает однополостный гиперболоид с одним из двух семейств прямых на нём.
Victor Kleptsyn
15:01
Вот интересно, нельзя ли как-то красиво "выйти в трёхмерное пространство" — чтобы движение точки по окружности и соответствующее движение серединного перпендикуляра естественно становилось движением образующей по гиперболоиду?
Victor Kleptsyn
15:05
Да, про движение образующей — есть удивительная на первый взгляд модель-иллюстрация, когда прямая-образующая "прокручивается" сквозь кривую — гиперболическую — щель: https://youtu.be/gNG-UmfdB4o?t=633 (я поставил отметку начала на нужное место).
Victor Kleptsyn
М
16:03
Математические байки
In reply to this message
А ещё коллеги добавляют, что картинка для эллипса тоже напоминает однополостный гиперболоид, только на который мы смотрим вдоль одного из направлений внутри полости (точнее, внутри его асимптотического конуса).
Victor Kleptsyn
19 November 2020
М
12:04
Математические байки
Н
Непрерывное математическое образование 17.11.2020 12:28:21
https://t.me/EtudesRu/26
«50 лет назад, 17 ноября 1970 года на поверхность Луны был доставлен советский аппарат «Луноход-1» (…). Ясно, что такой громадный проект наполнен сложными математикой и физикой: от проектирования самого аппарата до расчёта полёта к Луне. Но не все знают, что на каждом луноходе было установлено устройство, принцип работы которого построен на совсем «школьной» программе (…)»
как всегда по вторникам — новый сюжет у Математических этюдов
«50 лет назад, 17 ноября 1970 года на поверхность Луны был доставлен советский аппарат «Луноход-1» (…). Ясно, что такой громадный проект наполнен сложными математикой и физикой: от проектирования самого аппарата до расчёта полёта к Луне. Но не все знают, что на каждом луноходе было установлено устройство, принцип работы которого построен на совсем «школьной» программе (…)»
как всегда по вторникам — новый сюжет у Математических этюдов
Victor Kleptsyn
М
12:28
Математические байки
Кстати, всего на Луне сейчас есть пять (комплектов) отражателей — по одному блоку на Луноходах-1 и -2, и три установили экспедиции Apollo-11, -14 и -15.
Я пишу "комплектов" — потому что каждый из них это не один такой трёхгранный уголок, а блок из них. У Луноходов это вынесенный вперёд блок в виде продолговатого шестиугольника (вот тут, https://commons.wikimedia.org/wiki/File:Lunokhod-2_model.jpg , он в направлении фотографа, а вот тут, https://www.roscosmos.ru/29563/ — самый левый).
Я пишу "комплектов" — потому что каждый из них это не один такой трёхгранный уголок, а блок из них. У Луноходов это вынесенный вперёд блок в виде продолговатого шестиугольника (вот тут, https://commons.wikimedia.org/wiki/File:Lunokhod-2_model.jpg , он в направлении фотографа, а вот тут, https://www.roscosmos.ru/29563/ — самый левый).
Victor Kleptsyn
12:29
Собственно, вот он (image credit: https://commons.wikimedia.org/wiki/File:Lunokhod-2_model.jpg , фрагмент) —
Victor Kleptsyn
12:31
А вот фотография (с Луны!) установленного астронавтами Apollo-14 блока (image credit: NASA, https://science.nasa.gov/science-news/science-at-nasa/2004/06may_lunarranging/ ) :
Victor Kleptsyn
М
12:47
Математические байки
In reply to this message
Так что на Луне есть целых пять точек, расстояние до которых сейчас люди умеют измерять с точностью до сантиметров и даже до миллиметров (см. https://iopscience.iop.org/article/10.1086/596748 ). И в той статье в "Природе" 2002 года, которую упоминают в Этюдах, есть карта их расположения на Луне (Image credit: Е.Ю.Алёшкина, "Лазерная локация Луны", https://priroda.ras.ru/pdf/2002-09.pdf ) —
Victor Kleptsyn
М
13:16
Вот цитата из другой статьи 2002 года, https://ilrs.gsfc.nasa.gov/docs/williams_lw13.pdf ("неясно, то ли отражатели потеряли эффективность, то ли положение неточное") :
Victor Kleptsyn
13:25
А в 2010 году — нашли: https://ucsdnews.ucsd.edu/archive/newsrel/science/04-26SovietReflector.asp !
И давайте я добавлю пару цитату оттуда:
==
“It turns out we were searching around a position miles from the rover,” said Murphy. “We could only search one football-field-sized region at a time. The recent images from LRO, together with laser altimetry of the surface, provided coordinates within 100 meters, and then we were in business and only had to wait for time on the telescope in good observing conditions.”
==
"The best signal we’ve seen from Lunokhod 2 in several years of effort is 750 return photons, but we got about 2,000 photons from Lunokhod 1 on our first try. It’s got a lot to say after almost 40 years of silence.”
(Кстати, интересно, что счёт идёт буквально на отдельные фотоны!)
И давайте я добавлю пару цитату оттуда:
==
“It turns out we were searching around a position miles from the rover,” said Murphy. “We could only search one football-field-sized region at a time. The recent images from LRO, together with laser altimetry of the surface, provided coordinates within 100 meters, and then we were in business and only had to wait for time on the telescope in good observing conditions.”
==
"The best signal we’ve seen from Lunokhod 2 in several years of effort is 750 return photons, but we got about 2,000 photons from Lunokhod 1 on our first try. It’s got a lot to say after almost 40 years of silence.”
(Кстати, интересно, что счёт идёт буквально на отдельные фотоны!)
Victor Kleptsyn
М
14:00
Математические байки
И — понятно, зачем для этого нужны отражатели: до Луны далеко, так что "рассеянный во все стороны свет" просто был бы совершенно незаметен на этом расстоянии. (Впрочем, вспомнилось из физического юмора — https://what-if.xkcd.com/13/ )
Да — собственно про расстояние: расстояние от Земли до Луны это в среднем ~380.000 км. Можно, конечно, его так и запоминать — но гораздо более "говорящий" способ измерения это "чуть больше световой секунды". Так что экипажам, командовавшим Луноходами с Земли, было не очень просто — даже минимальная задержка управления была бы ~2.5 секунды (ибо сигнал оттуда + туда). "Была бы" — потому что изображение оттуда тоже приходило не постоянным потоком, а "один кадр в несколько секунд".
Да — собственно про расстояние: расстояние от Земли до Луны это в среднем ~380.000 км. Можно, конечно, его так и запоминать — но гораздо более "говорящий" способ измерения это "чуть больше световой секунды". Так что экипажам, командовавшим Луноходами с Земли, было не очень просто — даже минимальная задержка управления была бы ~2.5 секунды (ибо сигнал оттуда + туда). "Была бы" — потому что изображение оттуда тоже приходило не постоянным потоком, а "один кадр в несколько секунд".
Victor Kleptsyn
14:07
In reply to this message
(Коллеги ругаются, что я про 2000 фотонов написал как про не очень большое количество — говоря, что как же так, что вот человеческий глаз в полной темноте десяток фотонов уже ловит. Так что давайте я добавлю, что в цитате там от Лунохода-2 — 750 фотонов это лучшее, что видели, а ещё чуть ниже по той же ссылке упоминают, что в полнолуние возвращается ещё в 10 раз меньше: "Near full moon, the strength of the returning light decreases by a factor of ten," he adds. "We need to understand what is causing this if we are contemplating putting additional scientific equipment on the moon. Finding the Lunokhod 1 reflector will add important clues to this study.")
Victor Kleptsyn
20 November 2020
М
16:58
Математические байки
In reply to this message
Гугл сегодня порадовал дудлом ко дню рождения Бенуа Мандельброта:
https://www.google.com/doodles/benoit-mandelbrots-96th-birthday
Правда, увы, на заглавной Гугла он появляется, кажется, только во Франции — но по ссылке выше должно бы работать везде.
https://www.google.com/doodles/benoit-mandelbrots-96th-birthday
Правда, увы, на заглавной Гугла он появляется, кажется, только во Франции — но по ссылке выше должно бы работать везде.
Victor Kleptsyn
21 November 2020
М
14:06
Математические байки
In reply to this message
У меня осталась неоконченная история про скатерть Улама. Мы начали спираль с числа 41 вместо 1 — и увидели достаточно длинную диагональ из одних простых чисел.
Ну и я тогда закончил этот рассказ на вопросе — а будет ли эта диагональ из простых продолжаться дальше?
Ну и я тогда закончил этот рассказ на вопросе — а будет ли эта диагональ из простых продолжаться дальше?
Victor Kleptsyn
14:06
In reply to this message
Для начала давайте поймём, что эта диагональ не может и дальше состоять только из простых чисел. А именно — не очень сложно понять, что n-е число на диагонали задаётся как P(n)=n^2-n+41.
Victor Kleptsyn
14:08
Но ни один многочлен от n не может принимать только простые значения. Например, значения многочлена P(n) выше автоматически делится на 41, если n делится на 41.
И понятно, что такое рассуждение работает для любого другого многочлена, если у него свободный член по модулю не равен 1. А если равен, то можно сдвинуть начало отсчёта; если P это многочлен с целыми коэффициентами и P(a)=p — простое, то P(a+pk) делится на p при любом k.
И понятно, что такое рассуждение работает для любого другого многочлена, если у него свободный член по модулю не равен 1. А если равен, то можно сдвинуть начало отсчёта; если P это многочлен с целыми коэффициентами и P(a)=p — простое, то P(a+pk) делится на p при любом k.
Victor Kleptsyn
14:09
Так что буквальный ответ на вопрос, будет ли — нет, не будет, более того, как раз следующее число на диагонали (а я не случайно оборвал картинку, когда диагональ дошла до ещё простого P(40)=39*40+41=1601 🙂 ) это P(41)=41^2 — не простое. И кстати, следующее за ним P(42)=41*43 — тоже.
Но это только начало истории, и не одной!
Но это только начало истории, и не одной!
Victor Kleptsyn
14:14
Вот для p=41 значения многочлена n^2-n+p, — числа, которые мы видим на диагонали из центра для начинающейся с числа p скатерти Улама, — оказались простыми для всех n=1,2,...,p-1 — оборвавшись только на том n=p, где не могли не оборваться. А ещё такие p бывают?
Victor Kleptsyn
14:19
In reply to this message
Да, а вот картинка с подписанными числами, продолженная чуть-чуть дальше.
Victor Kleptsyn
14:23
In reply to this message
Оказывается, что бывают — но только меньшие, p=41 из них наибольшее. Что, конечно, совершенно неочевидно. Вот картинка для p=17:
Victor Kleptsyn
14:25
Как раз все числа от P(1)=17 до P(16)=15*16+17=257 — простые, а первыми составными оказываются P(17)=17^2 и P(18)=17*19.
Victor Kleptsyn
14:33
(И p=2, 3 и 5, кстати, но тут картинка получается не очень впечатляющей: для p=5 там всего 4 значения, для p=3 два, для p=2 вообще одно. Но я их тут всё-таки упомяну — потому что они укладываются в общий принцип.)
Victor Kleptsyn
14:42
Так вот — а зачем вообще (кроме общей красоты скатерти Улама) я так внимательно смотрю на эти простые числа? Дело в том, что отсюда открывается дорога к однозначности разложения на простые в кольцах целых квадратичных расширений.
Классический вопрос о том, какие числа n представляются в виде суммы двух квадратов, связан с гауссовыми целыми числами — числами вида a+bi, составляющими кольцо Z[i].
Ибо (a+bi)(a-bi)=a^2+b^2, и условие про то, что все простые вида 4k+3 в разложении n должны быть в чётной степени, как раз связано с тем, что они при переходе в Z[i] остаются простыми, а 2 и простые вида 4k+1 — нет, "разваливаются" (например, 2=(1+i)(1-i), 5=(1+2i)(1-2i)).
И при работе со всем этим ключевую роль играет то, что в гауссовых целых Z[i] есть алгоритм Евклида и, как следствие, однозначность разложения на их простые.
Классический вопрос о том, какие числа n представляются в виде суммы двух квадратов, связан с гауссовыми целыми числами — числами вида a+bi, составляющими кольцо Z[i].
Ибо (a+bi)(a-bi)=a^2+b^2, и условие про то, что все простые вида 4k+3 в разложении n должны быть в чётной степени, как раз связано с тем, что они при переходе в Z[i] остаются простыми, а 2 и простые вида 4k+1 — нет, "разваливаются" (например, 2=(1+i)(1-i), 5=(1+2i)(1-2i)).
И при работе со всем этим ключевую роль играет то, что в гауссовых целых Z[i] есть алгоритм Евклида и, как следствие, однозначность разложения на их простые.
Victor Kleptsyn
14:43
Так будет не всегда — и стандартный пример состоит в том, что если вместо i=\sqrt{-1} к целым числам добавить \sqrt{-5}, то однозначность разложения на множители нарушится:
(1+\sqrt{-5})(1-\sqrt{-5}) = 6 = 2*3.
(1+\sqrt{-5})(1-\sqrt{-5}) = 6 = 2*3.
Victor Kleptsyn
14:54
Кстати, разложение на простые пытались применить и к теореме Ферма: пытаясь доказать, что у уравнения
x^p+y^p=z^p
нет нетривиальных решений — очень естественно добавить к целым числам корень p-й степени из 1,
\zeta=\exp(2πi/p),
разложить левую часть как произведение (x+\zeta^j y) по j=0,1...,p-1, и попробовать что-нибудь вытащить, сопоставляя разложения на множители в правой и в левой части.
И тут нужно начинать говорить слова "идеалы", ключевым именем тут будет Куммер, и я оставлю ссылку вот на этот короткий текст Кита Конрада —
https://kconrad.math.uconn.edu/blurbs/gradnumthy/fltreg.pdf
(Получается так доказать не для всех простых — так что пришлось ждать ещё 150 лет до доказательства Уайлса — но для многих.)
[+Картинка выше: несколько первых абзацев из текста Конрада.]
x^p+y^p=z^p
нет нетривиальных решений — очень естественно добавить к целым числам корень p-й степени из 1,
\zeta=\exp(2πi/p),
разложить левую часть как произведение (x+\zeta^j y) по j=0,1...,p-1, и попробовать что-нибудь вытащить, сопоставляя разложения на множители в правой и в левой части.
И тут нужно начинать говорить слова "идеалы", ключевым именем тут будет Куммер, и я оставлю ссылку вот на этот короткий текст Кита Конрада —
https://kconrad.math.uconn.edu/blurbs/gradnumthy/fltreg.pdf
(Получается так доказать не для всех простых — так что пришлось ждать ещё 150 лет до доказательства Уайлса — но для многих.)
[+Картинка выше: несколько первых абзацев из текста Конрада.]
Victor Kleptsyn
15:09
Кстати, ещё можно спрашивать не какие числа представимы как a^2+b^2 (т.е. какие квадраты длин бывают для отрезков между точками квадратной решётки), а какие числа представимы как a^2+ab+b^2 (т.е. какие квадраты длин бывают для отрезков между точками треугольной решётки).
И тут на помощь придут числа Эйзенштейна Z[w], где w=\exp(2πi/3)= -1/2 + i sqrt{3}/2.
В которых тоже есть алгоритм Евклида — и, значит, однозначность разложения на (их) простые!
И тут на помощь придут числа Эйзенштейна Z[w], где w=\exp(2πi/3)= -1/2 + i sqrt{3}/2.
В которых тоже есть алгоритм Евклида — и, значит, однозначность разложения на (их) простые!
Victor Kleptsyn
М
15:35
Математические байки
Так вот — а как обстоят дела с однозначностью разложения на простые в других квадратичных расширениях? Если добавлять к целым числам только \sqrt{-d}, то плохо. Но если мы рассмотрим квадратичное расширение Q[\sqrt{-d}] поля рациональных чисел — то есть множество чисел вида a+b\sqrt{-d}, где a и b рациональные — то там более естественно посмотреть на алгебраические целые числа. А при d=4k+3 это не только такие комбинации с целыми a и b, но и с одновременно полуцелыми: число z=(-1+\sqrt{-d})/2 является корнем уравнения z^2+z+ (d+1)/4 =0
И где-то мы такой многочлен уже видели, правда, вместо (d+1)/4 стояло p...
И где-то мы такой многочлен уже видели, правда, вместо (d+1)/4 стояло p...
Victor Kleptsyn
М
17:14
Математические байки
А если более аккуратно — то давайте посмотрим, чему равна норма числа (z+n) — то есть произведение (n+z) на его сопряжённый:
P(n)=(z+n) (\bar{z}+n) = (n- 1/2)^2 + (\sqrt{d}/2)^2 = n^2 -n +1/4 + d/4 = n^2 - n +p,
если p=(d+1)/4.
Поэтому если при малых n это произведение не простое, P(n)=ab, то в кольце целых O(\sqrt{-d}) у нас появится такая же неоднозначность с разложением на простые, что и раньше в Z[\sqrt{-5}] — потому что будет
ab= P(n) = (z+n) (\bar{z}+n)
(и из-за того, что норма z+n ещё маленькая, ни на что дальше сомножители в правой части раскладываться не могут).
Оказывается (и в детали я тут вдаваться не буду) — что на самом деле это критерий: все числа n^2-n+p для n=1,2,...,p-1 простые тогда и только тогда, когда в кольце целых O(\sqrt{1-4p}) есть однозначность разложения на простые. А число d, для которого в O(\sqrt{-d}) есть однозначность разложения, называется числом Хегнера ( Heegner number ) ; оказывается, что их таких ровно 9:
1, 2, 3, 7, 11, 19, 43, 67, 163.
P(n)=(z+n) (\bar{z}+n) = (n- 1/2)^2 + (\sqrt{d}/2)^2 = n^2 -n +1/4 + d/4 = n^2 - n +p,
если p=(d+1)/4.
Поэтому если при малых n это произведение не простое, P(n)=ab, то в кольце целых O(\sqrt{-d}) у нас появится такая же неоднозначность с разложением на простые, что и раньше в Z[\sqrt{-5}] — потому что будет
ab= P(n) = (z+n) (\bar{z}+n)
(и из-за того, что норма z+n ещё маленькая, ни на что дальше сомножители в правой части раскладываться не могут).
Оказывается (и в детали я тут вдаваться не буду) — что на самом деле это критерий: все числа n^2-n+p для n=1,2,...,p-1 простые тогда и только тогда, когда в кольце целых O(\sqrt{1-4p}) есть однозначность разложения на простые. А число d, для которого в O(\sqrt{-d}) есть однозначность разложения, называется числом Хегнера ( Heegner number ) ; оказывается, что их таких ровно 9:
1, 2, 3, 7, 11, 19, 43, 67, 163.
Victor Kleptsyn
М
17:41
Математические байки
In reply to this message
А ещё три последних числа в этом списке — совершенно случайно, чистейшей воды совпадение! — появлялись в той байке, которую я рассказывал почти сразу после скатерти Улама: в рассказе про почти целые числа.
Victor Kleptsyn
17:44
В той затравке предлагалось посмотреть на три числа вида e^{π\sqrt{d}), где d=163, 67 или 43. И во всех трёх случаях оказывалось, что после запятой заметное количество (а в первом случае даже просто много!) девяток.
Victor Kleptsyn
17:46
Давайте я покажу кадр из видео Ричарда Борчердса, https://youtu.be/a9k_QmZbwX8?t=197 .
Victor Kleptsyn
17:49
In reply to this message
Думаю, при взгляде на всё написанное становится понятно, что "таких совпадений не бывает".
И, как и в случае с числом (1+\sqrt{2})^100, механизм "почти целости" тут — что есть по-настоящему целое число, которое складывается из "почти целого" — и чего-то очень маленького.
И, как и в случае с числом (1+\sqrt{2})^100, механизм "почти целости" тут — что есть по-настоящему целое число, которое складывается из "почти целого" — и чего-то очень маленького.
Victor Kleptsyn
17:53
(В скобках — каюсь, я довольно долго считал, что e^{π\sqrt{163}) это такое случайное совпадение, ну вот написали что-то, и попали близко к целому; и даже то, что девяток после запятой ну слишком много, меня в те годы не настораживало.)
Victor Kleptsyn
М
18:22
Математические байки
Так вот — есть такая функция, j-инвариант. Это "хороший" инвариант эллиптической кривой — то есть фактора C/Г комплексной плоскости по решётке Г; иными словами, "хорошая" функция на множестве решёток на плоскости, рассматриваемых с точностью до умножения на комплексные числа (потому что умножение на λ переводит решётку C/Г в решётку C/(λГ)).
Её можно строить разными способами, но я сначала просто поверю в то, что она есть, и скажу про пару её свойств.
В частности — можно в решётке выбрать положительно ориентированный базис, и поделить на первый его элемент; тогда решётка примет вид <1, τ>, где τ — точка из верхней полуплоскости {Im τ>0}. Соответственно, тогда нужно строить функцию j(τ) в верхней полуплоскости — но инвариантную относительно замены базиса. А это не только замена τ-> τ+1 (что очевидно), но и вообще все действие SL(2,Z) перевыборами базиса:
τ-> (aτ+b)/(cτ+d),
где a,b,c,d целые и ad-bc=1.
Её можно строить разными способами, но я сначала просто поверю в то, что она есть, и скажу про пару её свойств.
В частности — можно в решётке выбрать положительно ориентированный базис, и поделить на первый его элемент; тогда решётка примет вид <1, τ>, где τ — точка из верхней полуплоскости {Im τ>0}. Соответственно, тогда нужно строить функцию j(τ) в верхней полуплоскости — но инвариантную относительно замены базиса. А это не только замена τ-> τ+1 (что очевидно), но и вообще все действие SL(2,Z) перевыборами базиса:
τ-> (aτ+b)/(cτ+d),
где a,b,c,d целые и ad-bc=1.
Victor Kleptsyn
18:25
Но уж раз j(τ) инвариантна относительно замены τ->τ+1, то можно рассматривать j как функцию на факторе верхней полуплоскости по этому сдвигу. А это — проколотый диск с координатой q=exp(2πi*τ); проколотый, потому что чем больше мнимая часть τ, тем меньше модулю q, но нулевым он никогда не будет.
Victor Kleptsyn
18:27
Так вот: если взять j-инвариант для решётки O(\sqrt{-d}), и в O(\sqrt{-d}) есть однозначное разложение на множители — то получающееся число (по нетривиальным причинам) в точности целое!
Victor Kleptsyn
М
19:54
Математические байки
Но — функцию j(q) в координате q можно в окрестности q=0 (отвечающему стремящейся к бесконечности мнимой части τ — то есть очень "неравномерным", "вертикально-вытянутым" решёткам) раскладывать в ряд. И как оказывается, ряд для j(q) начинается с 1/q (чем более решётка неравномерная, тем больше инвариант) — а дальше уже идут неотрицательные степени:
j(q)=1/q + 744 + 196844*q +... .
Для решётки целых O(\sqrt{-d}) второй вектор это τ=-1/2 + i \sqrt{d}/2, и соответственно
q= exp(2πi τ) = exp(-πi - π\sqrt{d}) = - 1/ exp(π\sqrt{d}) —
как раз почти те числа, что нам нужны!
j(q)=1/q + 744 + 196844*q +... .
Для решётки целых O(\sqrt{-d}) второй вектор это τ=-1/2 + i \sqrt{d}/2, и соответственно
q= exp(2πi τ) = exp(-πi - π\sqrt{d}) = - 1/ exp(π\sqrt{d}) —
как раз почти те числа, что нам нужны!
Victor Kleptsyn
19:58
И, соответственно, для каждого d=43, 67, 163 целое (отрицательное) число j(q) это огромная величина
1/q=-exp(π\sqrt{d}),
отличающаяся от нашей знаком, к которой добавляется 744, и ряд по положительным степеням q — которые, наоборот, уже очень маленькие. Вот отсюда и получаются
...743,9999...,
которые мы видим до и после запятой — и поэтому девяток у exp(π\sqrt{163}) больше, чем у exp(π\sqrt{67}).
1/q=-exp(π\sqrt{d}),
отличающаяся от нашей знаком, к которой добавляется 744, и ряд по положительным степеням q — которые, наоборот, уже очень маленькие. Вот отсюда и получаются
...743,9999...,
которые мы видим до и после запятой — и поэтому девяток у exp(π\sqrt{163}) больше, чем у exp(π\sqrt{67}).
Victor Kleptsyn
20:01
Ещё один кадр из того же видео Борчердса: https://youtu.be/a9k_QmZbwX8?t=623 ; кстати — не так часто у фидлсовского медалиста (и не только — https://en.wikipedia.org/wiki/Richard_Borcherds ) есть свой канал на YouTube :)
Victor Kleptsyn
М
20:17
Математические байки
In reply to this message
Вообще-то говоря, рассказ выше немного "повисает в воздухе", потому что я продекларировал функцию — j-инвариант, которую совсем не построил (и потому про которую пока в принципе непонятно, как что-либо проверять). Поэтому давайте я про неё скажу пару слов.
Вот если у нас есть решётка Г на комплексной плоскости и целое число k, то можно попробовать посчитать сумму обратных k-ых степеней ненулевых элементов решётки. И обозначить эту сумму через G_k(Г).
При нечётном k мы получим ноль — просто всё сократится. При k=2 сумма не будет абсолютно сходящейся, так что давайте её просто не рассматривать. А вот при чётных k>2 получается величина, хорошо зависящая от решётки. Правда, не инвариантная при перемасштабировании:
G_k(λГ) = λ^{-k} G_k(Г).
Ну так и давайте возьмём G_4^3(Г) и G_6^2(Г). Оба при умножении решётки на λ будут умножаться на λ^{-12} — а значит, их отношение это инвариант!
Это ещё не j-инвариант, но j-инвариант от этого отличается всего лишь на дробно-линейное преобразование: например, мы хотим, чтобы инвариант стремился к бесконечности, когда решётка становится всё более вырожденной, и поэтому в знаменателе будет не чистое G_6^2 или G_4^3, а некоторая их линейная комбинация (и даже понятно, какая — когда τ убегает на бесконечность, G_4 стремится к удвоенному \zeta(4), а G_6 к удвоенному \zeta(6), ну и остаётся подобрать коэффициенты, чтобы знаменатель обратился в ноль).
Вот если у нас есть решётка Г на комплексной плоскости и целое число k, то можно попробовать посчитать сумму обратных k-ых степеней ненулевых элементов решётки. И обозначить эту сумму через G_k(Г).
При нечётном k мы получим ноль — просто всё сократится. При k=2 сумма не будет абсолютно сходящейся, так что давайте её просто не рассматривать. А вот при чётных k>2 получается величина, хорошо зависящая от решётки. Правда, не инвариантная при перемасштабировании:
G_k(λГ) = λ^{-k} G_k(Г).
Ну так и давайте возьмём G_4^3(Г) и G_6^2(Г). Оба при умножении решётки на λ будут умножаться на λ^{-12} — а значит, их отношение это инвариант!
Это ещё не j-инвариант, но j-инвариант от этого отличается всего лишь на дробно-линейное преобразование: например, мы хотим, чтобы инвариант стремился к бесконечности, когда решётка становится всё более вырожденной, и поэтому в знаменателе будет не чистое G_6^2 или G_4^3, а некоторая их линейная комбинация (и даже понятно, какая — когда τ убегает на бесконечность, G_4 стремится к удвоенному \zeta(4), а G_6 к удвоенному \zeta(6), ну и остаётся подобрать коэффициенты, чтобы знаменатель обратился в ноль).
Victor Kleptsyn
20:21
Да, вот эти ряды из обратных k-ых степеней называются рядами Эйзенштейна (https://en.wikipedia.org/wiki/Eisenstein_series ) ; а ещё с ними иногда удобнее работать, сразу поделив на их предел в бесконечности (или в точке прокола q=0, если работать в q-координате) :
E_{2k}(Г) = G_{2k}(Г) / 2\zeta(2k).
E_{2k}(Г) = G_{2k}(Г) / 2\zeta(2k).
Victor Kleptsyn
20:28
И вот теперь с j-инвариантом уже хотя бы в принципе можно работать — уже видно, из каких частей он собран. Вообще, есть очень хороший текст Грина, "The Ramanujan Constant", http://people.maths.ox.ac.uk/greenbj/papers/ramanujanconstant.pdf — как раз этому эффекту почти-целости и посвящённый.
И вот один кусочек оттуда — как раз про j-инвариант:
И вот один кусочек оттуда — как раз про j-инвариант:
Victor Kleptsyn
20:31
Да, а текст Грина называется так, потому что именно так называется exp(π\sqrt{163}) (см., например, https://mathworld.wolfram.com/RamanujanConstant.html ).
Victor Kleptsyn
М
20:49
Математические байки
In reply to this message
А ещё j-инвариант оказывается связан с группой-Монстром, самой большой из спорадических (т.е. "не включённых в серии") простых групп. Например, наименьшая размерность, в которой Монстр умеет действовать нетривиальными линейными преобразованиями (размерность наименьшего нетривиального представления) — это 196883. Если сравнить с рядом для j-инварианта, то видно, что от коэффициента при q это отличается на 1. И опять-таки, "таких совпадений не бывает" — но если одно это совпадение кажется недостаточно убедительным, то есть ещё простое соотношение между следующей размерностью и коэффициентом при q^2 у j-инварианта. А ещё размерность представления — это след тождественного преобразования в ней, а можно посмотреть, какие следы будут у действий других элементов, и обнаружить там сходство с некоторыми аналогами j-инварианта...
Victor Kleptsyn
М
22:07
Математические байки
Давайте я закончу этот рассказ ссылкой на посвящённое Monstrous Moonshine (более сложное!) видео Борчердса — https://youtu.be/5Mg25JK31wE?t=1433 — и покажу ещё один кадр из него.
Victor Kleptsyn
М
22:31
Математические байки
И на этом эту нашу "прогулку", начавшуюся со скатерти Улама и на которой мы "прошли" через многочлен Эйлера n^2+n+41, константу Рамануджана exp(π\sqrt{163}), разложение на простые в кольце целых O(\sqrt{-163}), через j-инвариант, через ряды Эйзенштейна E_{2k}, и где возникли группа-Монстр и Monstrous Moonshine, — так вот, на этом нашу сегодняшнюю прогулку, кажется, можно завершить.
Victor Kleptsyn
24 November 2020
М
12:02
Математические байки
In reply to this message
В прошлый раз мы прошли по одной тропинке, начинающейся с этого вопроса; а в этот раз давайте пройдём по другой, начинающейся со слов "простые числа" и "значения многочлена".
Не-постоянный многочлен одной переменной, как мы видели, не может принимать в целых точках только простые значения. То же самое правда для многочлена нескольких переменных — иначе можно просто выбрать какое-нибудь направление и рассмотреть P(n,n,n) или P(n,2n,3n), и т. д. — сведя эту невозможность к уже доказанной невозможности для многочлена одной переменной.
Ну или можно перенести одномерное доказательство: сказать, что если для многочлена P с целыми коэффициентами выполнено
P(n_1,...,n_k)=p,
то для любых a_1,...,a_k значение
P(n_1+a_1 p,...,n_k+ a_k p) делится на p,
и почти ни при каких a_j простым поэтому быть не может.
Но — если нас интересуют простые числа, то можно автоматически отбрасывать неположительные значения. Для многочленов одной переменной тогда уже можно получить больше одного простого значения: 17-10*n^2 принимает положительные значения 17 и 7 — и все положительные значения простые. Но вот все простые числа (и даже просто бесконечное их число) получить так, чтобы все положительные значения были простыми, у многочлена одной переменной не получится.
А что, если переменных много? Оказывается, тогда такой многочлен существует!
Не-постоянный многочлен одной переменной, как мы видели, не может принимать в целых точках только простые значения. То же самое правда для многочлена нескольких переменных — иначе можно просто выбрать какое-нибудь направление и рассмотреть P(n,n,n) или P(n,2n,3n), и т. д. — сведя эту невозможность к уже доказанной невозможности для многочлена одной переменной.
Ну или можно перенести одномерное доказательство: сказать, что если для многочлена P с целыми коэффициентами выполнено
P(n_1,...,n_k)=p,
то для любых a_1,...,a_k значение
P(n_1+a_1 p,...,n_k+ a_k p) делится на p,
и почти ни при каких a_j простым поэтому быть не может.
Но — если нас интересуют простые числа, то можно автоматически отбрасывать неположительные значения. Для многочленов одной переменной тогда уже можно получить больше одного простого значения: 17-10*n^2 принимает положительные значения 17 и 7 — и все положительные значения простые. Но вот все простые числа (и даже просто бесконечное их число) получить так, чтобы все положительные значения были простыми, у многочлена одной переменной не получится.
А что, если переменных много? Оказывается, тогда такой многочлен существует!
Victor Kleptsyn
12:05
И вот на картинке выше явный пример такого многочлена — которому посвящена статья James P. Jones, Daihachiro Sato, Hideo Wada and Douglas Wiens, "Diophantine Representation of the Set of Prime Numbers", The American Mathematical Monthly, 83 :6 (1976), pp. 449-464 ; https://www.tandfonline.com/doi/abs/10.1080/00029890.1976.11994142
Victor Kleptsyn
12:15
На самом деле — можно задать вопрос, какие вообще множества представляются как множества положительных значений многочленов (от нескольких переменных) с целыми коэффициентами в целых точках.
(Такие множества называются диофантовыми .)
Понятно, что для любого многочлена P такое множество перечислимо: есть алгоритм, который рано или поздно напечатает все его элементы (быть может, не по порядку). Потому что мы просто будем обходить всю целочисленную решётку и проверять, положительное ли значение P в этой точке, а если да, то печатать.
(Такие множества называются диофантовыми .)
Понятно, что для любого многочлена P такое множество перечислимо: есть алгоритм, который рано или поздно напечатает все его элементы (быть может, не по порядку). Потому что мы просто будем обходить всю целочисленную решётку и проверять, положительное ли значение P в этой точке, а если да, то печатать.
Victor Kleptsyn
12:21
Да — можно смотреть значения многочленов в точках с целыми координатами, а можно в точках с неотрицательными целыми. И хотя для конкретного многочлена это могут быть разные множества — на то, какие множества так вообще получается представить, этот выбор не влияет: если искомое множество X уже представлено как множество положительных значений P на Z^n, то оно же будет множеством положительных значений Q на (Z_+)^n, где
Q(a_1,b_1,...,a_n,b_n) = P(a_1-b_1,...,a_n-b_n).
И наоборот, если искомое множество X уже представлено как множество положительных значений P на (Z_+)^n, то оно же будет множеством положителных значений Q на Z^4n, где
Q(a_1,b_1,c_1,d_1,...,a_n,b_n,c_n,d_n) =
P(a_1^2+b_1^2+c_1^2+d_1^2,...,a_n^2+b_n^2+c_n^2+d_n^2).
Так что я дальше буду считать, что нас интересуют значения на Z_+^n.
Q(a_1,b_1,...,a_n,b_n) = P(a_1-b_1,...,a_n-b_n).
И наоборот, если искомое множество X уже представлено как множество положительных значений P на (Z_+)^n, то оно же будет множеством положителных значений Q на Z^4n, где
Q(a_1,b_1,c_1,d_1,...,a_n,b_n,c_n,d_n) =
P(a_1^2+b_1^2+c_1^2+d_1^2,...,a_n^2+b_n^2+c_n^2+d_n^2).
Так что я дальше буду считать, что нас интересуют значения на Z_+^n.
Victor Kleptsyn
12:24
Например, множество составных чисел диофантово, и это совсем просто увидеть: достаточно взять
P(a,b)=(a+2)(b+2).
Как раз множество положительных значений P на Z_+^2 все составные числа и даст.
Но — а будет ли диофантовым, например, множество совершенных чисел? А множество простых делителей чисел вида 2^{2^n}+1 ?
P(a,b)=(a+2)(b+2).
Как раз множество положительных значений P на Z_+^2 все составные числа и даст.
Но — а будет ли диофантовым, например, множество совершенных чисел? А множество простых делителей чисел вида 2^{2^n}+1 ?
Victor Kleptsyn
12:31
Теорема, получающаяся из объединения работ Мартина Дэвиса, Юрия Владимировича Матиясевича, Хилари Патнема и Джулии Робинсон, утверждает, что перечислимость — единственное(!) необходимое условие:
Теорема [M. Davis, Ю. В. Матиясевич, H. Putnam, J. Robinson]
Любое перечислимое множество диофантово. Более того, порождающий его многочлен P может быть построен по алгоритму перечисления алгоритмическим образом.
Теорема [M. Davis, Ю. В. Матиясевич, H. Putnam, J. Robinson]
Любое перечислимое множество диофантово. Более того, порождающий его многочлен P может быть построен по алгоритму перечисления алгоритмическим образом.
Victor Kleptsyn
М
12:50
Математические байки
Всё это восходит к десятой проблеме Гильберта:
Пусть дано полиномиальное уравнение от нескольких переменных с целыми коэффициентами. Проверить алгоритмически, есть ли у него решения в целых числах.
(На картинке выше — соответствующий абзац из книги "Проблемы Гильберта", издания 1969 года)
Пусть дано полиномиальное уравнение от нескольких переменных с целыми коэффициентами. Проверить алгоритмически, есть ли у него решения в целых числах.
(На картинке выше — соответствующий абзац из книги "Проблемы Гильберта", издания 1969 года)
Victor Kleptsyn
М
13:38
Математические байки
In reply to this message
Если бы такой способ проверки существовал — например, его применение позволяло бы для любого фиксированного n>2 доказать теорему Ферма (потому что это вопрос о разрешимости полиномиального уравнения x^n+y^n-z^n=0). Было бы возможно за конечное время (и без дополнительных идей) как-то проверять, представимо ли число в виде суммы трёх кубов целых чисел (которые могут быть и отрицательными, так что это не конечная проверка), например, представимы ли 33 (https://www.quantamagazine.org/sum-of-three-cubes-problem-solved-for-stubborn-number-33-20190326 , https://people.maths.bris.ac.uk/~maarb/papers/cubesv1.pdf ) или 42 (https://www.youtube.com/watch?v=ASoz_NuIvP0 ).
Позволять проверить существование решения в натуральных числах у уравнения
x/(y+z) + y/(z+x) + z/(x+y) = 4
(если вы не видели, то это совершенно прекрасная история — см. https://t.me/cme_channel/198 + https://habr.com/ru/post/335248/ + https://www.quora.com/How-do-you-find-the-integer-solutions-to-frac-x-y+z-+-frac-y-z+x-+-frac-z-x+y-4/answer/Alon-Amit?share=1 ).
И так далее.
Позволять проверить существование решения в натуральных числах у уравнения
x/(y+z) + y/(z+x) + z/(x+y) = 4
(если вы не видели, то это совершенно прекрасная история — см. https://t.me/cme_channel/198 + https://habr.com/ru/post/335248/ + https://www.quora.com/How-do-you-find-the-integer-solutions-to-frac-x-y+z-+-frac-y-z+x-+-frac-z-x+y-4/answer/Alon-Amit?share=1 ).
И так далее.
Victor Kleptsyn
М
13:58
Математические байки
In reply to this message
Так вот — теорема Дэвиса, Матиясевича, Патнема и Робинсон даёт отрицательное решение проблемы Гильберта — утверждая, что такого алгоритма в принципе существовать не может.
Victor Kleptsyn
14:00
In reply to this message
Потому что перечислимые множества это совершенно не то же самое, что разрешимые (принадлежность которым можно проверить за конечное число операций). И первый пример тут — множество кодов программ, которые когда-нибудь останавливаются, перечислимо (ибо можно запустить симулятор + перебор кодов + параллелизацию), но не разрешимо (ибо теорема Тьюринга и парадокс лжеца).
Victor Kleptsyn
14:06
In reply to this message
Ну и прежде, чем обсуждать, почему это так, давайте ещё чуть-чуть посмотрим на эту формулу. И заметим, что эта формула для простых чисел... для удобства пользователя разложена на множители!
Victor Kleptsyn
14:08
In reply to this message
Но если присмотреться, то видно, что вторая скобка это 1 минус сумма квадратов. Поэтому, если значение P положительное, то вторая скобка должна быть равна 1, а каждый квадрат внутри неё должен обращаться в ноль.
Поэтому эту теорему можно переформулировать так: число k+2 простое тогда и только тогда, когда существуют (все остальные переменные), для которых выполняется (система полиномиальных уравнений):
Поэтому эту теорему можно переформулировать так: число k+2 простое тогда и только тогда, когда существуют (все остальные переменные), для которых выполняется (система полиномиальных уравнений):
Victor Kleptsyn
14:16
Поэтому более правильно определять диофантовость так: подмножество A в Z_+^k называется диофантовым, если существует многочлен P(a_1,...,a_k,x_1,...,x_n), такой, что
(a_1,...,a_k) из A <=> существуют (x_1,...,x_n) из Z_+^n, для которых
P(a_1,...,a_k,x_1,...,x_n)=0.
(а систему из нескольких диофантовых уравнений можно свернуть в одно взятием суммы их квадратов)
(a_1,...,a_k) из A <=> существуют (x_1,...,x_n) из Z_+^n, для которых
P(a_1,...,a_k,x_1,...,x_n)=0.
(а систему из нескольких диофантовых уравнений можно свернуть в одно взятием суммы их квадратов)
Victor Kleptsyn
М
15:28
Математические байки
Более того, если чуть-чуть расширить класс многочленов до экспоненциальных многочленов, разрешив ещё возводить одну переменную в степень другой, то такой многочлен строится совсем "вручную".
Для начала вообще представим себе, что мы имеем право использовать ещё операцию "факториал". Как тогда можно задать простоту числа p?
Во-первых, нужно попросить, чтобы p было не меньше 2. Ну, тут мы уже видели, как это сделать: одно из уравнений системы будет
p=k+2.
А как проверить, что p не делится ни на что, кроме 1 и себя? Цикл использовать нельзя — но можно вместо него воспользоваться факториалом. А именно — давайте посмотрим на (p-1)! ; число p простое тогда и только тогда, когда оно взаимно просто с (p-1)!, а это проверяется алгоритмом Евклида:
a*(p-1)!-b*p=1.
На самом деле, теорема Валлиса утверждает, что простота p равносильна сравнимости (p-1)! с (-1) по модулю p, так что одну переменную можно сэкономить, и написать просто
(p-1)!+1-b*p=0.
Для начала вообще представим себе, что мы имеем право использовать ещё операцию "факториал". Как тогда можно задать простоту числа p?
Во-первых, нужно попросить, чтобы p было не меньше 2. Ну, тут мы уже видели, как это сделать: одно из уравнений системы будет
p=k+2.
А как проверить, что p не делится ни на что, кроме 1 и себя? Цикл использовать нельзя — но можно вместо него воспользоваться факториалом. А именно — давайте посмотрим на (p-1)! ; число p простое тогда и только тогда, когда оно взаимно просто с (p-1)!, а это проверяется алгоритмом Евклида:
a*(p-1)!-b*p=1.
На самом деле, теорема Валлиса утверждает, что простота p равносильна сравнимости (p-1)! с (-1) по модулю p, так что одну переменную можно сэкономить, и написать просто
(p-1)!+1-b*p=0.
Victor Kleptsyn
15:36
In reply to this message
И пара (k,b) тут — "сертификат простоты" числа p, который есть для всех простых p и только для них.
А как быть, если наш бюрократ не понимает факториалы? Нужно "соотношение факториальности" как-нибудь выразить:
p=k+2
c+1-b*p=0
//а тут какие-нибудь уравнения, задающие c=(p-1)! //
А через что мы можем факториал выразить, где он появляется? Первое, что приходит в голову — биномиальные коэффициенты. И действительно, если нам нужно r!, а число M очень большое, то посмотрим на
C_M^r = M(M-1)...(M-r+1) / r!
А как быть, если наш бюрократ не понимает факториалы? Нужно "соотношение факториальности" как-нибудь выразить:
p=k+2
c+1-b*p=0
//а тут какие-нибудь уравнения, задающие c=(p-1)! //
А через что мы можем факториал выразить, где он появляется? Первое, что приходит в голову — биномиальные коэффициенты. И действительно, если нам нужно r!, а число M очень большое, то посмотрим на
C_M^r = M(M-1)...(M-r+1) / r!
Victor Kleptsyn
15:38
Тогда отношение
M^r / (C_M^r)
чуть-чуть больше r! ; поэтому если M^r на C_M^r поделить с остатком, то при всех достаточно больших M мы как раз r! и получим.
M^r / (C_M^r)
чуть-чуть больше r! ; поэтому если M^r на C_M^r поделить с остатком, то при всех достаточно больших M мы как раз r! и получим.
Victor Kleptsyn
15:42
А деление с остатком мы выразить можем: чтобы q было неполным частным от деления A на B, нужно, чтобы выполнялись неравенства
A>=B*q
и
A<B*(q+1)
А нестрогое неравенство — это равенство, если добавить к меньшей части ещё одну свободную переменную (а для строгого нужно ещё 1 добавить). Итого соотношение q=r! выражается системой на неотрицательные целые переменные
// M достаточно большое относительно r, //
M^r = q*(C_M^r) + x_1,
(q+1)*(C_M^r) = M^r + 1 + x_2
A>=B*q
и
A<B*(q+1)
А нестрогое неравенство — это равенство, если добавить к меньшей части ещё одну свободную переменную (а для строгого нужно ещё 1 добавить). Итого соотношение q=r! выражается системой на неотрицательные целые переменные
// M достаточно большое относительно r, //
M^r = q*(C_M^r) + x_1,
(q+1)*(C_M^r) = M^r + 1 + x_2
Victor Kleptsyn
15:44
Чтобы добиться исходной цели — задать простоту с помощью экспоненциальных многочленом — остаётся выразить соотношение c=C_M^r. Но биномиальный коэффициент это коэффициент в биноме Ньютона. Так давайте возьмём ну очень большое (относительно M и r) число N и посмотрим на (N+1)^M.
Victor Kleptsyn
15:45
Если взять неполное частное q' при делении на N^r, а потом остаток от деления q' на N — то как раз C_M^r и будет. А и неполное частное, и остаток мы выражать уже умеем!
Victor Kleptsyn
16:00
И если это всё сделать — мы получим систему экспоненциально-полиномиальных уравнений, таких, что для p найдутся все остальные (неотрицательные целые) переменные тогда и только тогда, когда p простое. Ура!
Собственно, мой рассказ выше это пересказ [части] статьи Ю. В. Матиясевича в "Кванте" в 1975 году — http://kvant.mccme.ru/1975/05/formuly_dlya_prostyh_chisel.htm
Собственно, мой рассказ выше это пересказ [части] статьи Ю. В. Матиясевича в "Кванте" в 1975 году — http://kvant.mccme.ru/1975/05/formuly_dlya_prostyh_chisel.htm
Victor Kleptsyn
М
16:29
Математические байки
In reply to this message
Возвращаясь к диофантовости всех перечислимых множеств — собственно говоря, идея "сертификата" работает и тут.
А именно — представим себе, что какая-то машина долго-долго работала и наконец закончила работу. Давайте соберём все состояния её "регистров" во все моменты времени в один "протокол" ("в момент времени t=1 состояние такое-то; в момент t=2 состояние такое-то; ..."). Так вот — машина заканчивает работу за конечное время тогда и только тогда, когда существует конечный "протокол", в котором в начальный момент времени стоит её начальное состояние, корректно выполнен переход от каждого момента к следующему, и конечное состояние соответствует команде "стоп". Этот "протокол" мы и захотим добавить в дополнительные переменные.
Правда, мы не знаем, сколько машина будет работать — но не страшно, просто пусть у нас будет система счисления с большим-большим основанием N, а последовательные состояния машины — последовательными "цифрами" в записи одной из переменных в этой системе счисления. Собственно, мы уже применили почти этот подход к выражению биномиальных коэффициентов — только тогда мы "доставали" из большого числа (N+1)^M одну его цифру, а тут придётся научиться работать со всеми цифрами одновременно, каким-то образом одновременно обеспечивая, что переход от каждого момента времени t к следующему t+1 корректен.
В качестве одного из шагов возникает теорема Куммера о делимости биномиальных коэффициентов на простые:
А именно — представим себе, что какая-то машина долго-долго работала и наконец закончила работу. Давайте соберём все состояния её "регистров" во все моменты времени в один "протокол" ("в момент времени t=1 состояние такое-то; в момент t=2 состояние такое-то; ..."). Так вот — машина заканчивает работу за конечное время тогда и только тогда, когда существует конечный "протокол", в котором в начальный момент времени стоит её начальное состояние, корректно выполнен переход от каждого момента к следующему, и конечное состояние соответствует команде "стоп". Этот "протокол" мы и захотим добавить в дополнительные переменные.
Правда, мы не знаем, сколько машина будет работать — но не страшно, просто пусть у нас будет система счисления с большим-большим основанием N, а последовательные состояния машины — последовательными "цифрами" в записи одной из переменных в этой системе счисления. Собственно, мы уже применили почти этот подход к выражению биномиальных коэффициентов — только тогда мы "доставали" из большого числа (N+1)^M одну его цифру, а тут придётся научиться работать со всеми цифрами одновременно, каким-то образом одновременно обеспечивая, что переход от каждого момента времени t к следующему t+1 корректен.
В качестве одного из шагов возникает теорема Куммера о делимости биномиальных коэффициентов на простые:
Victor Kleptsyn
М
17:05
Математические байки
И если вот этим путём (на который я, конечно, пока только намекнул) пройти — то получается
Теорема (Davis, Putnam, Robinson, 1961; https://doi.org/10.2307/1970289 )
Любое перечислимое множество экспоненциально-диофантово.
Но что делать с экспонентой? Как выразить хоть что-то экспоненциальное, если у нас в руках только многочлены? Ну хоть что-нибудь экспоненциально растущее — скажем, уже было известно, что если есть какое-то отношение, которое растёт быстрее, чем u^k при любом k, но медленнее, чем u^u, то этого уже хватает. Но как это вытащить из полиномов? И полноте, возможно ли это? [Это сейчас мы знаем, что да — а вот обзор в Mathematical Reviews на их работу в этом смысле не горит энтузиазмом...]
И — последний удар!
Теорема (Ю.В. Матиясевич, 1970; см. http://mi.mathnet.ru/dan35274 )
Отношение "v — 2u-е число Фибоначчи" диофантово.
Теорема (Davis, Putnam, Robinson, 1961; https://doi.org/10.2307/1970289 )
Любое перечислимое множество экспоненциально-диофантово.
Но что делать с экспонентой? Как выразить хоть что-то экспоненциальное, если у нас в руках только многочлены? Ну хоть что-нибудь экспоненциально растущее — скажем, уже было известно, что если есть какое-то отношение, которое растёт быстрее, чем u^k при любом k, но медленнее, чем u^u, то этого уже хватает. Но как это вытащить из полиномов? И полноте, возможно ли это? [Это сейчас мы знаем, что да — а вот обзор в Mathematical Reviews на их работу в этом смысле не горит энтузиазмом...]
И — последний удар!
Теорема (Ю.В. Матиясевич, 1970; см. http://mi.mathnet.ru/dan35274 )
Отношение "v — 2u-е число Фибоначчи" диофантово.
Victor Kleptsyn
17:08
Два кусочка из статьи Матиясевича:
Victor Kleptsyn
17:08
И собственно явное задание —
Victor Kleptsyn
25 November 2020
М
12:48
Математические байки
In reply to this message
Собственно, эта статья замечательна тем, что её можно спокойно разобрать сильному школьнику.
Вот основные идеи:
а) Соотношение x^2-xy-y^2=1 на неотрицательные x и y равносильно тому, что x и y это два последовательных числа Фибоначчи, x=F_{2m+1}, y=F_{2m}. А если бы в правой части было (-1), то было бы x=F_{2m}, y=F_{2m-1}.
Утверждение само по себе симпатичное — и мгновенно доказывающееся по индукции (достаточно написать, что x=y+z).
И тут можно посмотреть на равенства (2) и (3) из кусочка выше — гарантирующие, что l, z, g и h это числа Фибоначчи.
Вот основные идеи:
а) Соотношение x^2-xy-y^2=1 на неотрицательные x и y равносильно тому, что x и y это два последовательных числа Фибоначчи, x=F_{2m+1}, y=F_{2m}. А если бы в правой части было (-1), то было бы x=F_{2m}, y=F_{2m-1}.
Утверждение само по себе симпатичное — и мгновенно доказывающееся по индукции (достаточно написать, что x=y+z).
И тут можно посмотреть на равенства (2) и (3) из кусочка выше — гарантирующие, что l, z, g и h это числа Фибоначчи.
Victor Kleptsyn
13:00
б) Делимость чисел Фибоначчи. Во-первых, F_m делится на F_n тогда и только тогда, когда m делится на n. Что несложно увидеть, приведя числа Фибоначчи по модулю F_n: будет
номер — 0, 1, 2, ..., n-1, n, n+1,...
число — 0, 1, 1, ..., * , 0, * , ...,
и после n будет то же, что и после нуля, только умноженное на F_{n-1} (взаимно простое с F_n).
Но вот — и это ключевой шаг — если F_m делится не просто на F_n, а на F_n^2, то вот это равносильно тому, что номер m делится на nF_n.
номер — 0, 1, 2, ..., n-1, n, n+1,...
число — 0, 1, 1, ..., * , 0, * , ...,
и после n будет то же, что и после нуля, только умноженное на F_{n-1} (взаимно простое с F_n).
Но вот — и это ключевой шаг — если F_m делится не просто на F_n, а на F_n^2, то вот это равносильно тому, что номер m делится на nF_n.
Victor Kleptsyn
13:01
In reply to this message
И вот здесь начинает возникать экспоненциальный сдвиг: возникает связь между номерами и соответствующими числами Фибоначчи — а это как раз экспонента с основанием в золотое сечение.
И тут можно посмотреть на условие (4) из теоремы — как раз гарантирующее, что номер числа g делится на само число l.
И тут можно посмотреть на условие (4) из теоремы — как раз гарантирующее, что номер числа g делится на само число l.
Victor Kleptsyn
М
13:37
Математические байки
In reply to this message
в) И третья идея — нужно как-то суметь связать число Фибоначчи v с его номером 2u, причём в виде именно равенства. Для этого — для ещё одного, очень большого, числа m запускается ещё одна рекуррентная последовательность:
ψ_0=0, ψ_1=1, ψ_{k+1}= m ψ_k - ψ_{k-1}.
Точно так же, как для чисел Фибоначчи, свойство чисел (x,y) быть последовательной парой чисел оттуда проверяется полиномиально: необходимо и достаточно, чтобы
x^2 - m*xy + y^2 =1.
(Без условия целочисленности получилась бы гипербола — так что это описание того, как выглядят целочисленные точки на ней)
ψ_0=0, ψ_1=1, ψ_{k+1}= m ψ_k - ψ_{k-1}.
Точно так же, как для чисел Фибоначчи, свойство чисел (x,y) быть последовательной парой чисел оттуда проверяется полиномиально: необходимо и достаточно, чтобы
x^2 - m*xy + y^2 =1.
(Без условия целочисленности получилась бы гипербола — так что это описание того, как выглядят целочисленные точки на ней)
Victor Kleptsyn
13:43
Так вот — давайте эту последовательность ψ_k приводить по какому-нибудь модулю, по которому m чему-нибудь хорошему равно. А именно: если m сравнимо с 2 по модулю N, то приведение по модулю N превращает соотношение на ψ_k в
ψ_{k+1}= 2 ψ_k - ψ_{k-1},
а это соотношение арифметической прогрессии. Поэтому тогда ψ_k сравнимо со своим номером k.
А если m сравнимо с 3 по модулю N, то соотношение превращается в
ψ_{k+1}= 3 ψ_k - ψ_{k-1},
а это как раз соотношение на числа Фибоначчи F_{2k} с чётными номерами! То есть ψ_k сравнимо с F_{2k} по модулю N.
ψ_{k+1}= 2 ψ_k - ψ_{k-1},
а это соотношение арифметической прогрессии. Поэтому тогда ψ_k сравнимо со своим номером k.
А если m сравнимо с 3 по модулю N, то соотношение превращается в
ψ_{k+1}= 3 ψ_k - ψ_{k-1},
а это как раз соотношение на числа Фибоначчи F_{2k} с чётными номерами! То есть ψ_k сравнимо с F_{2k} по модулю N.
Victor Kleptsyn
13:47
In reply to this message
И если попросить, чтобы сравнивалось одно и то же число x — то как раз получится связать его номер и соответствующее число Фибоначчи.
Victor Kleptsyn
М
14:03
Математические байки
Условие (7) как раз говорит, что x — это одно из чисел последовательности ψ_k; условие (8) — что его номер k сравним с u; а условие (9) — что v сравнимо с F_{2k}. Так что если v=F_{2u}, то как раз можно взять x=ψ_{2u} — и остаётся достроить все остальные числа.
Victor Kleptsyn
М
15:48
Математические байки
In reply to this message
Остаётся аккуратно посмотреть, как из всех сравнимостей получается переход в другую сторону — но давайте я это замету под ковёр. И закончу рассказ добавлением пары ссылок:
*) вот тут — http://www.mathnet.ru/php/presentation.phtml?option_lang=rus&presentid=3647 — видеозаписи курса Матиясевича в ЛШСМ-2011
*) а вот тут — статья в "Кванте" 1970 года (первый год, когда "Квант" начал выходить!) Ф. Варпаховского и А. Колмогорова (да-да!), озаглавленная "О решении десятой проблемы Гильберта" — заканчивающаяся как раз предъявлением (но без подробного разбора) этой системы:
https://kvant.ras.ru/1970/07/o_reshenii_desyatoj_problemy_g.htm
*) вот тут — http://www.mathnet.ru/php/presentation.phtml?option_lang=rus&presentid=3647 — видеозаписи курса Матиясевича в ЛШСМ-2011
*) а вот тут — статья в "Кванте" 1970 года (первый год, когда "Квант" начал выходить!) Ф. Варпаховского и А. Колмогорова (да-да!), озаглавленная "О решении десятой проблемы Гильберта" — заканчивающаяся как раз предъявлением (но без подробного разбора) этой системы:
https://kvant.ras.ru/1970/07/o_reshenii_desyatoj_problemy_g.htm
Victor Kleptsyn
15:52
In reply to this message
Статья Jones-Sato-Wada-Wiens выйдет через 6 лет, в 1976 году.
Victor Kleptsyn
6 December 2020
М
11:01
Математические байки
Н
Непрерывное математическое образование 06.12.2020 10:51:34
картинки по выходным: замощения, доказывающие теоремы Тебо и Наполеона, из декабрьского Квантика
Victor Kleptsyn
М
16:06
Математические байки
Замечательный вопрос по теории вероятностей —
https://twitter.com/thienan496/status/1335534138959400961
Дублирую: подбросили 100 честных монет (не показывая результат). [Игроку] разрешается задать один вопрос вида "да/нет", и получить на него ответ. После этого у игрока про монеты одна за одной спрашивают "орёл или решка", и их открывают. За каждое верное угадывание он получает по доллару. Какой правильный вопрос надо задать, и какой стратегии следовать после того?
Осторожно, в комментариях спойлеры!
https://twitter.com/thienan496/status/1335534138959400961
Дублирую: подбросили 100 честных монет (не показывая результат). [Игроку] разрешается задать один вопрос вида "да/нет", и получить на него ответ. После этого у игрока про монеты одна за одной спрашивают "орёл или решка", и их открывают. За каждое верное угадывание он получает по доллару. Какой правильный вопрос надо задать, и какой стратегии следовать после того?
Осторожно, в комментариях спойлеры!
Victor Kleptsyn
8 December 2020
М
11:30
Математические байки
Н
Непрерывное математическое образование 08.12.2020 11:29:48
Сергей Миронович Натанзон (18.10.1948–07.12.2020)
Victor Kleptsyn
М
11:31
Математические байки
Меня он учил на 1-м курсе НМУ...
Victor Kleptsyn
М
14:45
Математические байки
Н
Непрерывное математическое образование 19.05.2020 13:54:56
картинка — пусть будет поводом поговорить немного про теорему Понселе
Victor Kleptsyn
М
М
14:45
Математические байки
Н
Непрерывное математическое образование 19.05.2020 13:59:13
Во-первых, напомним про лекцию В.Ю.Протасова «Теорема Понселе — яркая и загадочная» ( https://t.me/cme_channel/477 ) и его статью «Два века теоремы Понселе» в Кванте-2014 ( http://kvant.mccme.ru/pdf/2014/2014-56.pdf ).
Во-вторых, на менее элементарном уровне есть замечательное рассуждение, связывающая теорему Понселе с эллиптическими кривыми. Про это есть статья Гриффитса и Харриса ( http://publications.ias.edu/node/221 ). Но можно, например, посмотреть лекции Г.Б.Шабата на ЛШСМ (http://www.mathnet.ru/present9370 и далее).
Во-вторых, на менее элементарном уровне есть замечательное рассуждение, связывающая теорему Понселе с эллиптическими кривыми. Про это есть статья Гриффитса и Харриса ( http://publications.ias.edu/node/221 ). Но можно, например, посмотреть лекции Г.Б.Шабата на ЛШСМ (http://www.mathnet.ru/present9370 и далее).
Victor Kleptsyn
14:45
Н
Непрерывное математическое образование 20.05.2020 23:33:47
В третьих, есть «бильярдная» точка зрения на теорему Понселе — можно начать с лекции 28 книги «Математический дивертисмент» Табачникова и Фукса (и, заодно, можно заглянуть в лекцию 29 про теорему Понселе и другие теоремы о замыкании)
Victor Kleptsyn
М
17:03
Математические байки
In reply to this message
Давайте я добавлю пару слов про теорему Понселе; кажется, формулировку её я знал ещё то ли со школы, то ли с младших курсов универа, — но вот доказательство с мерой (первое из упоминающихся выше) узнал как раз от Протасова, из его лекции на олимпиаде Шарыгина (сразу после ЛШСМ-2018).
Формулируется она очень просто — пусть у нас есть две окружности, одна внутри другой. Мы берём точку на внешней окружности и начинаем из неё строить "звёздочку", каждый раз проводя касательную к внутренней окружности и продлевая её до второго пересечения с внешней.
Теорема Понселе утверждает, что если такая цепочка замкнётся для какой-то одной начальной точки, то она замкнётся для любой другой (и через такое же число шагов). Более того, то же самое верно и если вместо окружностей будут и просто коники ( = кривые второго порядка).
Формулируется она очень просто — пусть у нас есть две окружности, одна внутри другой. Мы берём точку на внешней окружности и начинаем из неё строить "звёздочку", каждый раз проводя касательную к внутренней окружности и продлевая её до второго пересечения с внешней.
Теорема Понселе утверждает, что если такая цепочка замкнётся для какой-то одной начальной точки, то она замкнётся для любой другой (и через такое же число шагов). Более того, то же самое верно и если вместо окружностей будут и просто коники ( = кривые второго порядка).
Victor Kleptsyn
17:05
Вот если бы окружности были концентрическими, то всё было бы понятно: чтобы "звёздочка" замкнулась, нужно, чтобы отсекаемый одним её звеном угол был бы соизмерим с 2π:
Victor Kleptsyn
17:05
(И если он равен 2π*p/q, то "звёздочка" замыкается через q шагов, сделав p оборотов.)
Victor Kleptsyn
17:06
Но — а что делать, если окружности не концентрические?
Victor Kleptsyn
17:20
И очень красивое доказательство, — его можно прочитать в статье Протасова в "Кванте" (http://kvant.mccme.ru/pdf/2014/2014-56.pdf ), но ещё и вот тут есть видеозапись (http://www.mathnet.ru/present19870 ) его лекции на закрытии ММО, и там же ( http://www.mathnet.ru:8080/PresentFiles/19870/protasov_poncelet.pdf ) выложены слайды от неё — так вот, очень красивое доказательство обобщает это рассуждение на случай общих окружностей с помощью инвариантных мер.
Вот его ключевой момент:
Лемма. На внешней окружности можно устроить такое распределение масс с некоторой линейной плотностью \rho(x), что полная масса дуги, отрезаемой любой касательной к внутренней окружности, всегда одна и та же.
Иными словами — представим себе, что внешняя окружность сделана из проволоки, причём переменной толщины. Так что линейная плотность у неё в одних точках одна, а в других другая. А внутренняя окружность — вкопанный гладкий столб. И мы по-разному отрубаем дугу внешней окружности секущей, проходящей впритирку к столбу.
Так вот — можно так подобрать эту переменную толщину проволоки (и, соответственно, переменную линейную плотность), что как бы мы ни отсекали дугу касательной к столбу, её полная масса будет одной и той же.
Вот его ключевой момент:
Лемма. На внешней окружности можно устроить такое распределение масс с некоторой линейной плотностью \rho(x), что полная масса дуги, отрезаемой любой касательной к внутренней окружности, всегда одна и та же.
Иными словами — представим себе, что внешняя окружность сделана из проволоки, причём переменной толщины. Так что линейная плотность у неё в одних точках одна, а в других другая. А внутренняя окружность — вкопанный гладкий столб. И мы по-разному отрубаем дугу внешней окружности секущей, проходящей впритирку к столбу.
Так вот — можно так подобрать эту переменную толщину проволоки (и, соответственно, переменную линейную плотность), что как бы мы ни отсекали дугу касательной к столбу, её полная масса будет одной и той же.
Victor Kleptsyn
17:29
И действительно, если эту лемму доказать, то понятно, какой должен быть критерий замыкания: если отсекаемая масса составляет (p/q) от полной массы внешней окружности, то для любой начальной точки мы замкнёмся через q шагов, сделав p оборотов, а если они несоизмеримы, то не замкнёмся никогда.
Victor Kleptsyn
М
17:45
Математические байки
А доказывается она явной конструкцией: эту плотность можно найти явно.
А именно — чтобы доказать, что функция "масса отрезаемой дуги" постоянна, нужно доказать, что её производная (при движении точки касания по внутренней окружности) равна нулю. То есть нам нужно проверить, что масса дуг FE и GH на картинке выше одинакова хотя бы в первом порядке, когда касательные очень близки.
А две "бесконечно близкие" касательные пересекаются в точке касания — поэтому "почти что" можно считать, что касательная "проворачивается" вокруг точки касания.
А именно — чтобы доказать, что функция "масса отрезаемой дуги" постоянна, нужно доказать, что её производная (при движении точки касания по внутренней окружности) равна нулю. То есть нам нужно проверить, что масса дуг FE и GH на картинке выше одинакова хотя бы в первом порядке, когда касательные очень близки.
А две "бесконечно близкие" касательные пересекаются в точке касания — поэтому "почти что" можно считать, что касательная "проворачивается" вокруг точки касания.
Victor Kleptsyn
17:59
In reply to this message
Посмотрим, с какими скоростями « бегут » точки A и B (на этой картинке, или F и G на картинке выше) по внешней окружности. Несложно видеть, что отношение этих скоростей как раз равно отношению KA/KB отрезков, на которые касательная делится точкой касания с внутренней окружностью. Потому что угол, на который мы поворачиваем, общий; дальше есть длина отрезка — как раз то, что нам нужно — и угол, под которым хорда врезается в окружность — но эти углы с двух сторон хорды одинаковы!
Victor Kleptsyn
18:01
Давайте тогда возьмём в качестве линейной плотности rho(x)=1/d(x), где d(x) — длина касательной к внутренней окружности из точки x наружной. Тогда « в первом приближении » при вращении касательной масса отрезаемой не будет меняться. Действительно, скорости точек A и B соотносятся как KA:KB, а плотности в этих точках как (1/KA):(1/KB), значит, сколько мы прибавляем за счёт движения A, столько же и теряем за счёт движения B.
Victor Kleptsyn
18:01
Поэтому производная полной массы отрезаемой дуги будет равна нулю — то есть сама эта масса постоянна, не зависит от выбора касательной к внутренней окружности. А этого-то мы и хотели!
Victor Kleptsyn
31 December 2020
М
17:21
Математические байки
Новогоднее видео от Mathologer про разбиения на доминошки:
Victor Kleptsyn
М
17:21
Математические байки
Н
Непрерывное математическое образование 27.12.2020 00:05:05
https://youtu.be/Yy7Q8IWNfHM
в качестве картинок по выходным — продолжение темы разбиений на домино, теоремы о полярном круге для ацтекского брильянта и проч.
в качестве картинок по выходным — продолжение темы разбиений на домино, теоремы о полярном круге для ацтекского брильянта и проч.
Victor Kleptsyn
М
17:23
Математические байки
Оно начинается с очень простых вещей (что шахматную доску без двух противоположных углов нельзя разрезать на доминошки), но продолжается очень содержательными.
Например — формулой для подсчёта количества разбиений доски mxn:
Например — формулой для подсчёта количества разбиений доски mxn:
Victor Kleptsyn
17:26
А вот тут — М. Н. Вялый, “Пфаффианы или искусство расставлять знаки…”, Матем. просв., сер. 3, 9, Изд-во МЦНМО, М., 2005, 129–142, http://mi.mathnet.ru/rus/mp/v9/s3/p129 — об этой формуле написано:
Victor Kleptsyn
17:29
Вот кадр для числа для доски 8x8 — и можно это сравнить с названием лекции С. К. Смирнова в ЛШСМ-2017 (https://www.mccme.ru/dubna/2017/courses/smirnov-lect.html )
Victor Kleptsyn
17:31
Вот кадр с детерминантной формулой — число способов разбивать на доминошки это определитель матрицы смежности между чёрными и белыми вершинами, только соседние элементы там бывают не только 1, но и i — чтобы их произведение компенсировало возникающий знак перестановки:
Victor Kleptsyn
17:34
(Правда, мне чуть больше по душе вариант расстановки, когда бывают все варианты, 1,-1,i,-i, потому что тогда появляется дискретный оператор комплексного дифференцирования, и становится понятно, откуда в дискретной задаче про доминошки — хотя бы в принципе — связь с комплексным анализом.)
Victor Kleptsyn
17:43
И это один из результатов, которым посвящена брошюра Е. Ю. Смирнова, "Три взгляда на ацтекский бриллиант" (https://www.mccme.ru/free-books/dubna/smirnov-aztec.pdf ); вот тут одно из доказательств — через функцию высоты:
Victor Kleptsyn
17:46
И под конец — поведение уголков, когда мы начинаем двигаться вместе с ними, стабилизируется в режим "замораживания":
Victor Kleptsyn
17:46
(И вот этого рассуждения я раньше не знал.)
Victor Kleptsyn
17:47
В общем — очень хорошее видео; хоть оно и длинное, но я очень советую его посмотреть (промотав начальную часть, если она слишком простая).
Victor Kleptsyn
М
18:04
Математические байки
Ну и вот тут мой собственный рассказ на малом ШАДе об асимптотической комбинаторике — о вопросах вида "сколько есть таких больших комбинаторных объектов" и "как такой типичный объект выглядит", и об ацтекском бриллианте в том числе: https://events.yandex.ru/events/m/mshad14?openTalkVideo=640-28 .
Victor Kleptsyn
1 January 2021
М
15:59
Математические байки
Давайте я чуть-чуть про ацтекский бриллиант добавлю: вот тут красивая картинка и пара ссылок —
Victor Kleptsyn
М
М
15:59
Математические байки
Н
Непрерывное математическое образование 26.02.2018 11:58:45
Про разбиения на домино (в т.ч. случайные) можно для начала заглянуть в статью Кеньона и Окунькова в колокне «What is…» (и потом читать, например, Lectures on Dimers) или в статью В.Горина «Что можно сложить из кубиков?» в Кванте.
А про подсчет количества разбиений на домино полезно почитать статью М.Вялого в Мат. просвещении (и конкретно про ацтекский бриллиант объясняется, конечно, в одноименной брошюре Е.Смирнова, упоминавшейся здесь в начале года).
А про подсчет количества разбиений на домино полезно почитать статью М.Вялого в Мат. просвещении (и конкретно про ацтекский бриллиант объясняется, конечно, в одноименной брошюре Е.Смирнова, упоминавшейся здесь в начале года).
Victor Kleptsyn
М
16:00
Математические байки
А вот тут мы его (и разбиения, и треугольные доминошки, и асимптотику количества) уже обсуждали: https://t.me/mathtabletalks/733
Victor Kleptsyn
3 January 2021
М
22:45
Математические байки
In reply to this message
Полгода назад я тут, по случаю лекции Этьена Жиса в "математических вечерах ЛШСМ", вспоминал его книгу "A singular mathematical promenade" — теорему Концевича о билете в метро, комбинаторную задачу с ответом из Плутарха и доказательство Гаусса основной теоремы алгебры.
А сейчас вышел её перевод на русский — и за это огромное спасибо выполнившему его Евгению Смирнову!
А сейчас вышел её перевод на русский — и за это огромное спасибо выполнившему его Евгению Смирнову!
Victor Kleptsyn
М
22:45
Математические байки
Н
Непрерывное математическое образование 29.12.2020 18:19:24
карта из недавно вышедшей «Математической прогулки с осмотром особенностей» Э.Жиса (пер. Е.Ю.Смирнов)
«Эта книга видного французского ученого — неформальное введение (в жанре «прогулки») в несколько разделов современной математики. Все темы, затронутые в книге, в большей или меньшей степени связаны с теорией особенностей. Читателю, прошедшему эту прогулку вместе с автором, она поможет выбрать раздел математики, в котором он будет специализироваться, — выбор предлагается широкий.»
https://biblio.mccme.ru/node/76199
«Эта книга видного французского ученого — неформальное введение (в жанре «прогулки») в несколько разделов современной математики. Все темы, затронутые в книге, в большей или меньшей степени связаны с теорией особенностей. Читателю, прошедшему эту прогулку вместе с автором, она поможет выбрать раздел математики, в котором он будет специализироваться, — выбор предлагается широкий.»
https://biblio.mccme.ru/node/76199
Victor Kleptsyn
6 January 2021
М
17:15
Математические байки
In reply to this message
Из той же лекции Протасова: оказывается, что таких "теорем о замыкании" — "если замкнулось из одной точки, то замкнётся за то же число шагов из любой другой" — есть ещё несколько. И каждую можно доказывать с помощью правильно выбранной инвариантной меры.
А именно — кроме теоремы Понселе:
- теорема Штейнера (или теорема о телефонном диске)
- теорема о кузнечике/блохе/зигзаге
А именно — кроме теоремы Понселе:
- теорема Штейнера (или теорема о телефонном диске)
- теорема о кузнечике/блохе/зигзаге
Victor Kleptsyn
17:16
Теорема Штейнера: вписываем окружности так, чтобы они касались внутренней и внешней окружностей, и следующая касалась бы предыдущей.
Victor Kleptsyn
17:20
Но тут можно обойтись и без инвариантной меры: инверсией сделать внешнюю и внутреннюю окружности концентрическими — а в этом случае утверждение становится очевидным.
Victor Kleptsyn
17:20
Теорема о кузнечике: кузнечик скачет между внутренней и внешней окружностями, каждый раз прыгая на одно и то же фиксированное расстояние.
Victor Kleptsyn
17:21
Так вот — оказывается, что все эти три теоремы (Понселе, Штейнер и кузнечик) следуют из одной, более общей — теоремы Эмха.
Victor Kleptsyn
17:25
Здесь проведены целых три окружности — через точку "средней" окружности δ проводятся окружности, касающиеся внутренней и внешней окружностей α_0, α_1. А один шаг — взятие следующего пересечения с δ.
Victor Kleptsyn
М
18:37
Математические байки
Почему из этой теоремы всё следует?
Если окружность α_1 станет большой-большой (и далеко-далеко), то окружности, которые её касаются, рядом с δ ("в конечной области") вырождаются в прямые — и вот мы получаем теорему Понселе для окружностей δ и α_0.
Если окружности α_0 и α_1 концентрические, то окружности, которые их касаются, имеют центры на третьей окружности α' и фиксированный радиус d. И вот теорема о кузнечике для δ и α' с шагом d.
Наконец, для теоремы Штейнера все точки касания лежат на одной окружности δ (ибо это так для концентрических + инвариантность относительно инверсий).
Если окружность α_1 станет большой-большой (и далеко-далеко), то окружности, которые её касаются, рядом с δ ("в конечной области") вырождаются в прямые — и вот мы получаем теорему Понселе для окружностей δ и α_0.
Если окружности α_0 и α_1 концентрические, то окружности, которые их касаются, имеют центры на третьей окружности α' и фиксированный радиус d. И вот теорема о кузнечике для δ и α' с шагом d.
Наконец, для теоремы Штейнера все точки касания лежат на одной окружности δ (ибо это так для концентрических + инвариантность относительно инверсий).
Victor Kleptsyn
18:39
(Иллюстрация к теореме Штейнера — опять же из слайдов лекции Протасова, http://www.mathnet.ru:8080/PresentFiles/19870/protasov_poncelet.pdf )
Victor Kleptsyn
18:51
И — теорема Эмха тоже может быть доказана с помощью инвариантной меры.
А именно — нужно взять в качестве плотности величину
1/\sqrt{|f_0(x) f_1(x)|},
где f_j — степень точки x относительно окружности α_j
Очень похоже на обратную величину к длине касательной, то есть 1/\sqrt{f_0(x)}, которая была в теореме Понселе!
А цитата на картинке — из статьи
Universal measure for Poncelet-type theorems, E. A. Avksentyev and V. Yu. Protasov, Proc. Amer. Math. Soc. 146 (2018); см. https://arxiv.org/pdf/1610.00276.pdf
А именно — нужно взять в качестве плотности величину
1/\sqrt{|f_0(x) f_1(x)|},
где f_j — степень точки x относительно окружности α_j
Очень похоже на обратную величину к длине касательной, то есть 1/\sqrt{f_0(x)}, которая была в теореме Понселе!
А цитата на картинке — из статьи
Universal measure for Poncelet-type theorems, E. A. Avksentyev and V. Yu. Protasov, Proc. Amer. Math. Soc. 146 (2018); см. https://arxiv.org/pdf/1610.00276.pdf
Victor Kleptsyn
18:53
Вот. С Новым Годом!
Victor Kleptsyn
11 January 2021
М
20:10
Математические байки
Н
Непрерывное математическое образование 11.01.2021 20:10:16
продолжаются Harvard CMSA Math Science Literature Lecture Series
в среду (13.01) в 17:00 по Москве — Don Zagier, Quantum topology and new types of modularity
The talk concerns two fundamental themes of modern 3-dimensional topology and their unexpected connection with a theme coming from number theory.
A deep insight of William Thurston in the mid-1970s is that the vast majority of complements of knots in the 3-sphere, or more generally of 3-manifolds, have a unique metric structure as hyperbolic manifolds of constant curvature -1, so that 3-dimensional topology is in some sense not really a branch of topology at all, but of differential geometry.
In a different direction, the work of Vaughan Jones and Ed Witten in the late 1980s gave rise to the field of Quantum Topology, in which new types of invariants of knot complements and 3-manifolds are introduced that have their origins in ideas coming from quantum field theory.
These two themes then became linked by Kashaev’s famous Volume Conjecture, now some 25 years old (…). About 10 years ago, I was led by numerical experiments to the discovery (…) the Volume Conjecture then became part of a bigger story saying that the new invariant has some sort of strange transformation property (…). This turned out to be only the beginning of a fascinating and multi-faceted story relating quantum invariants, q-series, modularity, and many other topics. In the talk, which is intended for a general mathematical audience, I would like to recount some parts of this story (…)
в среду (13.01) в 17:00 по Москве — Don Zagier, Quantum topology and new types of modularity
The talk concerns two fundamental themes of modern 3-dimensional topology and their unexpected connection with a theme coming from number theory.
A deep insight of William Thurston in the mid-1970s is that the vast majority of complements of knots in the 3-sphere, or more generally of 3-manifolds, have a unique metric structure as hyperbolic manifolds of constant curvature -1, so that 3-dimensional topology is in some sense not really a branch of topology at all, but of differential geometry.
In a different direction, the work of Vaughan Jones and Ed Witten in the late 1980s gave rise to the field of Quantum Topology, in which new types of invariants of knot complements and 3-manifolds are introduced that have their origins in ideas coming from quantum field theory.
These two themes then became linked by Kashaev’s famous Volume Conjecture, now some 25 years old (…). About 10 years ago, I was led by numerical experiments to the discovery (…) the Volume Conjecture then became part of a bigger story saying that the new invariant has some sort of strange transformation property (…). This turned out to be only the beginning of a fascinating and multi-faceted story relating quantum invariants, q-series, modularity, and many other topics. In the talk, which is intended for a general mathematical audience, I would like to recount some parts of this story (…)
Victor Kleptsyn
13 January 2021
М
22 January 2021
М
15:30
Математические байки
Несколько дней назад слушал доклад Тома Кемптона (Tom Kempton), и утащил оттуда красивую байку про числа Фибоначчи (хотя доклад был о более сложных вещах, конечно).
Давайте возьмём золотое сечение φ; оно удовлетворяет уравнению φ^2=φ+1.
Посмотрим на множество чисел вида a+bφ, где a и b целые (иными словами, на кольцо Z[φ]). Поскольку φ удовлетворяет уравнению φ^2=φ+1, на этом множестве действует умножение на φ:
φ(a+bφ) = b + (a+b) φ.
В частности, в координатах (a,b) это линейное преобразование. Причём то самое, которое переводит (F_{n-1},F_n) в (F_n,F_{n+1}).
(В частности, отсюда легко увидеть, что φ^n = F_{n-1} + F_n φ.)
Давайте возьмём золотое сечение φ; оно удовлетворяет уравнению φ^2=φ+1.
Посмотрим на множество чисел вида a+bφ, где a и b целые (иными словами, на кольцо Z[φ]). Поскольку φ удовлетворяет уравнению φ^2=φ+1, на этом множестве действует умножение на φ:
φ(a+bφ) = b + (a+b) φ.
В частности, в координатах (a,b) это линейное преобразование. Причём то самое, которое переводит (F_{n-1},F_n) в (F_n,F_{n+1}).
(В частности, отсюда легко увидеть, что φ^n = F_{n-1} + F_n φ.)
Victor Kleptsyn
15:31
Итерируя это преобразование и применяя его к начальной точке (0,1), мы видим все числа Фибоначчи (как раз все точки (F_{n-1},F_n)); и при обычном рассказе применяют линейную алгебру, говоря, что у этого преобразования есть два сохраняемых им направления — и выбрав их в качестве новых координатных осей, мы его диагонализуем.
Victor Kleptsyn
15:31
Так вот — можно изящно без линейной алгебры обойтись. Потому что тождество, что наше преобразование отвечает умножению на φ, оно справедливо не только для целых a и b, но и для вещественных. А потому — оно сохраняет прямую a+bφ=0. Более того, любую из семейства параллельных ей прямых a+bφ=C оно переводит в прямую a+bφ=(φC) из того же семейства, расположенную в φ раз дальше от 0.
Victor Kleptsyn
15:32
Но это одно сохраняющееся направление, а нужно два. Откуда взять второе? А вот откуда: чтобы написать наше отображение, мы воспользовались не самим золотым сечением φ, а только уравнением на него, φ^2=φ+1. А у этого уравнения есть второй корень, φ'=-1/φ.
Victor Kleptsyn
15:33
Поэтому если бы мы взяли Z[φ'] — мы получили бы то же самое отображение. А значит, оно сохраняет и прямую
a+b φ' = 0 – иными словами, прямую a-b/φ=0 —
переводя любую параллельную ей прямую
a+b φ' = C
в прямую из того же семейства
a+b φ' = -C/φ,
умножая C на φ'=(-1/φ).
a+b φ' = 0 – иными словами, прямую a-b/φ=0 —
переводя любую параллельную ей прямую
a+b φ' = C
в прямую из того же семейства
a+b φ' = -C/φ,
умножая C на φ'=(-1/φ).
Victor Kleptsyn
15:34
И вот мы и получили две сохраняющиеся прямые — и знаем, что если мы их выберем в качестве новых осей координат, то наше отображение одну координату, (a+bφ), будет умножать на φ, а вторую, (a-b/φ) — на (-1/φ). И отсюда сразу видно, почему не просто отношение последовательных чисел Фибоначчи стремится к золотому сечению — а даже разность φF_n - F_{n+1} стремится к нулю: потому что на каждой итерации она умножается на (-1/φ).
Victor Kleptsyn
15:37
Вот такая замена линейной алгебры на теорию чисел. Мне очень понравилось! (Хотя конечно, у Тома всё это было только ступенькой к тому, что ему на самом деле было нужно.)
Victor Kleptsyn
15:40
Да, ещё — Harvard CMSA Math Science Literature Lecture Series выложили видеозапись лекции Дона Загира: https://youtu.be/BBJiDZ8Dr6A . По-моему, было очень круто (и я точно буду пересматривать).
Victor Kleptsyn
26 January 2021
М
00:19
Математические байки
Н
Непрерывное математическое образование 26.01.2021 00:18:04
https://xaxam.livejournal.com/1388925.html
https://xaxam.livejournal.com/1389776.html
https://xaxam.livejournal.com/1389828.html
https://xaxam.livejournal.com/1390217.html
про геометрии
https://xaxam.livejournal.com/1389776.html
https://xaxam.livejournal.com/1389828.html
https://xaxam.livejournal.com/1390217.html
про геометрии
Victor Kleptsyn
27 January 2021
М
15:26
Математические байки
Чуть-чуть исторического — читаю сейчас "стокгольмские лекции" Поля Пенлеве (Paul Painlevé) :
Victor Kleptsyn
15:28
In reply to this message
Уже титульный лист интересен — "по приглашению Его Величества короля Швеции и Норвегии"
Victor Kleptsyn
М
15:54
Математические байки
Биография Пенлеве — тем более: математик, один из создателей аналитической теории дифференциальных уравнений, профессор... А также дважды премьер-министр Франции (причём первый раз — в 1917 году; мягко сказать, не самое простое время).
В скобках — мы сейчас отлично знаем великого математика Анри Пуанкаре; а его двоюродный брат, Раймон Пуанкаре, семь лет... проработал президентом Франции (с 1913 по 1920-й; так что первый раз премьером Пенлеве был при нём).
В скобках — мы сейчас отлично знаем великого математика Анри Пуанкаре; а его двоюродный брат, Раймон Пуанкаре, семь лет... проработал президентом Франции (с 1913 по 1920-й; так что первый раз премьером Пенлеве был при нём).
Victor Kleptsyn
М
16:31
Математические байки
In reply to this message
Введение к запискам стокгольмских лекций выглядит вполне обычно-типографски:
Victor Kleptsyn
16:32
А вот сразу за содержанием (которое идёт в конце введения) начинается красота:
Victor Kleptsyn
16:40
В самом конце стокгольских лекций Пенлеве обсуждает задачу n тел и доказывает, что в задаче трёх тел единственная проблема, которая может возникнуть с продолжимостью решения, это столкновение:
Victor Kleptsyn
М
17:01
Математические байки
Казалось бы, а что тут такого удивительного, вроде как дифференциальное уравнение и будет продолжаться, пока "не сломается". Но если мы под "столкновением" понимаем, что при приближении к критическому моменту у всех положений тел предел есть, и у хотя бы двух из них он совпадает — то бывает не только это! Возможно, у положения наших материальных точек просто не будет предела в этот момент.
Victor Kleptsyn
17:09
Так вот — оказывается, что это действительно возможно!
Victor Kleptsyn
3 February 2021
М
00:06
Математические байки
Н
Непрерывное математическое образование 03.02.2021 00:06:11
https://ium.mccme.ru/s21/s21.html
в понедельник (8 февраля) начинается семестр в Независимом Московском университете
формат будет смешанный: будут как очные, так и дистанционные¹ занятия; приглашаются, как обычно, все желающие серьезно заниматься; подробности появляются на сайте
¹ в качестве бонуса дистанционных занятий — например, курсы Игоря Пака и Леонида Петрова (которые физически находятся в Америке)
в понедельник (8 февраля) начинается семестр в Независимом Московском университете
формат будет смешанный: будут как очные, так и дистанционные¹ занятия; приглашаются, как обычно, все желающие серьезно заниматься; подробности появляются на сайте
¹ в качестве бонуса дистанционных занятий — например, курсы Игоря Пака и Леонида Петрова (которые физически находятся в Америке)
Victor Kleptsyn
М
00:10
Математические байки
Н
Непрерывное математическое образование 03.02.2021 00:10:10
Victor Kleptsyn
5 February 2021
М
17:31
Математические байки
In reply to this message
Давайте я закончу этот рассказ — посмотрим, как именно система уравнений небесной механики может "ломаться" без того, чтобы какие-то два (точечных) тела сталкивались. Для начала — а как вообще такое может происходить?
Пусть у нас есть конечное число материальных точек, которые друг с другом взаимодействуют по закону всемирного тяготения: сила, с которой взаимодействуют две частицы, равна
G m_1 m_2 / r_{12}^2.
Механика классическая, никакой теории относительности (и это важно).
Естественно, есть закон сохранения энергии. Если в какой-то момент у нас все расстояния между частицами не меньше какого-то \eps, а мы знаем полную энергию системы — то это даёт ограничение сверху на кинетическую энергию и потому на скорости частиц, а значит, ограничение снизу на время, в течение которого дифференциальное уравнение "точно не сломается".
Поэтому если система в какой-то момент t_* ломается, то наименьшее расстояние между частицами r_{min}(t) должно в этот момент стремиться к 0.
Но если особенность (т. е. то, как "ломается" решение) не типа столкновения (то есть не такого типа, что у всех частиц есть в этот момент предел, просто у каких-то частиц он совпадает), то у какой-то частицы в этот момент предела быть не должно. Значит, её скорость должна устремиться к бесконечности — а она должна начать "метаться" всё сильнее и сильнее ("как sin(1/x)").
Более того. Как показал в работе ещё 1908 года фон Цейпель (von Zeipel), если особенность не типа столкновения — то "линейный размер" системы (например, максимальное расстояние от точек до центра масс) должен в этот момент устремиться к бесконечности!
Наконец, когда мы приближаемся к моменту особенности — сила, с которой взаимодействуют далеко друг от друга отстоящие тела, на этом (очень маленьком) масштабе времени почти не влияет на их траектории. Так что мы практически смотрим на тела или их почти слипшиеся кластеры, которые могут двигаться только почти по прямым и как-то друг с другом "почти сталкиваться (и разлетаться)".
И — да полноте, а можно ли в такой ситуации обеспечить беготню (хотя бы) одного тела взад-вперёд, которая ещё и должна какие-то тела выбросить на бесконечность за конечное время?
Пусть у нас есть конечное число материальных точек, которые друг с другом взаимодействуют по закону всемирного тяготения: сила, с которой взаимодействуют две частицы, равна
G m_1 m_2 / r_{12}^2.
Механика классическая, никакой теории относительности (и это важно).
Естественно, есть закон сохранения энергии. Если в какой-то момент у нас все расстояния между частицами не меньше какого-то \eps, а мы знаем полную энергию системы — то это даёт ограничение сверху на кинетическую энергию и потому на скорости частиц, а значит, ограничение снизу на время, в течение которого дифференциальное уравнение "точно не сломается".
Поэтому если система в какой-то момент t_* ломается, то наименьшее расстояние между частицами r_{min}(t) должно в этот момент стремиться к 0.
Но если особенность (т. е. то, как "ломается" решение) не типа столкновения (то есть не такого типа, что у всех частиц есть в этот момент предел, просто у каких-то частиц он совпадает), то у какой-то частицы в этот момент предела быть не должно. Значит, её скорость должна устремиться к бесконечности — а она должна начать "метаться" всё сильнее и сильнее ("как sin(1/x)").
Более того. Как показал в работе ещё 1908 года фон Цейпель (von Zeipel), если особенность не типа столкновения — то "линейный размер" системы (например, максимальное расстояние от точек до центра масс) должен в этот момент устремиться к бесконечности!
Наконец, когда мы приближаемся к моменту особенности — сила, с которой взаимодействуют далеко друг от друга отстоящие тела, на этом (очень маленьком) масштабе времени почти не влияет на их траектории. Так что мы практически смотрим на тела или их почти слипшиеся кластеры, которые могут двигаться только почти по прямым и как-то друг с другом "почти сталкиваться (и разлетаться)".
И — да полноте, а можно ли в такой ситуации обеспечить беготню (хотя бы) одного тела взад-вперёд, которая ещё и должна какие-то тела выбросить на бесконечность за конечное время?
Victor Kleptsyn
17:31
Оказывается, что да! И очень правильная и красивая иллюстрация тут — вот такой опыт: если на улице (!) положить друг на друга баскетбольный и теннисный мяч и уронить, то в результате двойного соударения теннисный мяч подскочит довольно высоко. (NB: не надо это делать рядом с домами/окнами/чем-то легкобьющимся!)
Если вы этого никогда не делали — вот тут роняют стопку из трёх шаров:
https://youtu.be/2UHS883_P60?t=12
Если вы этого никогда не делали — вот тут роняют стопку из трёх шаров:
https://youtu.be/2UHS883_P60?t=12
Victor Kleptsyn
М
18:10
Математические байки
В качестве прикидки — давайте на секунду представим, что сначала баскетбольный шарик ударился о землю, а уже потом, через долю секунды, об него ударился шарик за ним. Тогда этот меньший шарик отскочит с почти утроенной скоростью!
(выкладки — можно пропустить или сделать самому)
Тогда верхний шарик летит вниз со скоростью v, а баскетбольный уже вверх с той же (почти) скоростью v. А при упругом соударении тяжелого объекта со скоростью u с сильно более лёгким, движущимся ему навстречу со скоростью v, лёгкий отскочит со скоростью (почти) 2u+v: вообще-то нужно переходить в систему центра масс, но когда один из объектов тяжёлый, можно просто перейти в его систему отсчёта. Там лёгкий с какой скоростью (u+v) летит, с такой и отскочит — но в другую сторону, так что возврат в исходную систему отсчёта добавит ещё одно u.
Собственно, это очень хорошо видно, если жонглировать мячиком для пинг-понга, подбивая его снизу ракеткой: если ракетка в момент приёма идёт "вниз", то шарик отскочит с меньшей скоростью, а если вперёд, то с большей.
(выкладки — можно пропустить или сделать самому)
Тогда верхний шарик летит вниз со скоростью v, а баскетбольный уже вверх с той же (почти) скоростью v. А при упругом соударении тяжелого объекта со скоростью u с сильно более лёгким, движущимся ему навстречу со скоростью v, лёгкий отскочит со скоростью (почти) 2u+v: вообще-то нужно переходить в систему центра масс, но когда один из объектов тяжёлый, можно просто перейти в его систему отсчёта. Там лёгкий с какой скоростью (u+v) летит, с такой и отскочит — но в другую сторону, так что возврат в исходную систему отсчёта добавит ещё одно u.
Собственно, это очень хорошо видно, если жонглировать мячиком для пинг-понга, подбивая его снизу ракеткой: если ракетка в момент приёма идёт "вниз", то шарик отскочит с меньшей скоростью, а если вперёд, то с большей.
Victor Kleptsyn
М
20:27
Математические байки
А аналогия совсем из небесной механики — это гравитационный маневр, когда станция пролетает мимо какого-нибудь другого небесного тела, и в связанной с ним системе отсчёта просто пролетает по гиперболе (аналог упругого соударения шарика с ракеткой), а в исходной системе отсчёта не только меняет направление, но и модуль скорости.
Кстати, чем более "издалека" мы смотрим, тем точнее аналогия с абсолютно упругим соударением двух шариков. Тут и там есть закон сохранения энергии и закон сохранения момента импульса. Когда два шарика далеко друг от друга — они уже почти не взаимодействуют; так не всё ли равно, как было устроено их взаимодействие — физическим соударением или тяготением?
Ещё интересно, что применяется гравитационный манёвр не только для того, чтобы набирать скорость и улетать далеко от Солнца (самый известный пример — те же Вояджеры), но и чтобы замедлиться: иначе к Меркурию или вообще к Солнцу не добраться, слишком большую скорость нужно сбросить.
(Кажется, осознал я это после статьи Валерии Сироты в "Квантике" про Меркурий, которая как раз с гравитационного манёвра начинается; конечно, когда оно сформулировано, то становится понятно, но как-то я раньше не задумывался, что тормозить тоже нужно так; кстати — текст про гравитационный манёвр [окончание + чуть более вводное начало] у неё там тоже очень хороший.)
И собственно, мы это видим и прямо сейчас — см. траектории солнечного зонда Parker и летящей к Меркурию миссии BepiColombo.
Кстати, чем более "издалека" мы смотрим, тем точнее аналогия с абсолютно упругим соударением двух шариков. Тут и там есть закон сохранения энергии и закон сохранения момента импульса. Когда два шарика далеко друг от друга — они уже почти не взаимодействуют; так не всё ли равно, как было устроено их взаимодействие — физическим соударением или тяготением?
Ещё интересно, что применяется гравитационный манёвр не только для того, чтобы набирать скорость и улетать далеко от Солнца (самый известный пример — те же Вояджеры), но и чтобы замедлиться: иначе к Меркурию или вообще к Солнцу не добраться, слишком большую скорость нужно сбросить.
(Кажется, осознал я это после статьи Валерии Сироты в "Квантике" про Меркурий, которая как раз с гравитационного манёвра начинается; конечно, когда оно сформулировано, то становится понятно, но как-то я раньше не задумывался, что тормозить тоже нужно так; кстати — текст про гравитационный манёвр [окончание + чуть более вводное начало] у неё там тоже очень хороший.)
И собственно, мы это видим и прямо сейчас — см. траектории солнечного зонда Parker и летящей к Меркурию миссии BepiColombo.
Victor Kleptsyn
6 February 2021
М
21:05
Математические байки
In reply to this message
В 1975 году появилась работа Mather и McGehee — в которой был построен пример такого странного поведения, но... для системы на прямой.
Естественный вопрос — как это на прямой?! Там же просто произойдёт столкновение и ничего интересного не будет.
Дело в том, что мы можем "вырождать" динамику в R^3: представим себе, что наши материальные точки движутся не совсем идеально по одной и той же прямой, а только очень близко к ней. И вообще, если у нас в R^3 две точки должны были столкнуться — можно чуть-чуть сдвинуть одну из них, чтобы она мимо другой промахнулась (и пролетела по гиперболе). А потом посмотреть, что происходит, когда сдвиг стремится к нулю.
Оказывается, что предел есть, и формулируется очень разумно. А именно, гипербола вырождается в пролёт туда-обратно (угол между её асимптотами стремится к развёрнутому), и в пределе мы получаем абсолютно упругое столкновению (изменение знака скоростей в момент столкновения в системе, связанной с их центром масс).
Естественный вопрос — как это на прямой?! Там же просто произойдёт столкновение и ничего интересного не будет.
Дело в том, что мы можем "вырождать" динамику в R^3: представим себе, что наши материальные точки движутся не совсем идеально по одной и той же прямой, а только очень близко к ней. И вообще, если у нас в R^3 две точки должны были столкнуться — можно чуть-чуть сдвинуть одну из них, чтобы она мимо другой промахнулась (и пролетела по гиперболе). А потом посмотреть, что происходит, когда сдвиг стремится к нулю.
Оказывается, что предел есть, и формулируется очень разумно. А именно, гипербола вырождается в пролёт туда-обратно (угол между её асимптотами стремится к развёрнутому), и в пределе мы получаем абсолютно упругое столкновению (изменение знака скоростей в момент столкновения в системе, связанной с их центром масс).
Victor Kleptsyn
21:09
Поэтому пока в системе происходят только попарные столкновения — за них динамику можно продолжать, заменяя каждое упругим соударением. В частности — можно запускать и динамику на прямой, где получается смесь между абсолютно упругими соударениями и динамикой притягивающихся точек.
Victor Kleptsyn
21:17
В качестве ответвления — даже если притяжения нет, а только точки движутся по прямой, получается интересная вещь: число соударений в простой конфигурации из стенки (т.е. бесконечной массы) и двух сильно разных масс оказывается связанной с числом π!
Вот статья Г. А. Гальперина об этом — https://www.maths.tcd.ie/~lebed/Galperin.%20Playing%20pool%20with%20pi.pdf — и видео 3blue1brown об этой задаче: https://www.youtube.com/watch?v=HEfHFsfGXjs
Вот статья Г. А. Гальперина об этом — https://www.maths.tcd.ie/~lebed/Galperin.%20Playing%20pool%20with%20pi.pdf — и видео 3blue1brown об этой задаче: https://www.youtube.com/watch?v=HEfHFsfGXjs
Victor Kleptsyn
21:19
Один кадр оттуда "для завлекательности"
(Image credit: 3blue1brown, https://www.youtube.com/watch?v=HEfHFsfGXjs )
(Image credit: 3blue1brown, https://www.youtube.com/watch?v=HEfHFsfGXjs )
Victor Kleptsyn
М
22:24
Математические байки
In reply to this message
Так вот — возвращаясь уже к динамике на прямой с учётом притяжения. Mather и McGehee построили пример, в котором система четырёх притягивающихся точек на прямой в конечный момент времени t_* "ломается" не через столкновение (а именно — три из масс разлетаются на бесконечность, предела у четвёртой нет), а во все меньшие моменты испытывала только попарные столкновения.
И ключевой момент это "почти тройное столкновение". Представим себе, что у нас сталкиваются три точки — но не одновременно (ибо это запрещено), а почти одновременно.
Представим себе, что третья точка, которая "чуть-чуть опаздывает" к столкновению, сильно легче первых двух. Тогда в момент, когда первые две разлетаются после столкновения с огромными скоростями (потому что они в этот момент очень близко), им навстречу несётся лёгкая третья. А мы уже видели такой сценарий!
Столкновение — и она получает в несколько раз большую скорость, как теннисный мячик, столкнувшийся с баскетбольным. Часть этой скорости "съест" гравитация, пока точки будут разлетаться обратно, но именно что часть. И в сухом остатке — в почти тройном столкновении третья лёгкая точка может улететь со сколь угодно большой скоростью.
И ключевой момент это "почти тройное столкновение". Представим себе, что у нас сталкиваются три точки — но не одновременно (ибо это запрещено), а почти одновременно.
Представим себе, что третья точка, которая "чуть-чуть опаздывает" к столкновению, сильно легче первых двух. Тогда в момент, когда первые две разлетаются после столкновения с огромными скоростями (потому что они в этот момент очень близко), им навстречу несётся лёгкая третья. А мы уже видели такой сценарий!
Столкновение — и она получает в несколько раз большую скорость, как теннисный мячик, столкнувшийся с баскетбольным. Часть этой скорости "съест" гравитация, пока точки будут разлетаться обратно, но именно что часть. И в сухом остатке — в почти тройном столкновении третья лёгкая точка может улететь со сколь угодно большой скоростью.
Victor Kleptsyn
М
22:45
Математические байки
И из этого уже понятно, как построить пример: берём 4 материальные точки
m1, m2, m3, m4,
в этом порядке, и пусть m3 в сравнении с остальными очень лёгкая, а в самом начале у m1, m2 и m3 будет почти тройное столкновение, из которого m3 вылетает с огромной скоростью v.
Тогда из-за закона сохранения энергии m1 и m2 остаются очень-очень близко друг к другу — откуда-то ведь нужно было взять эту энергию, а больше неоткуда. А из-за закона сохранения импульса эта "двойная система" из m1 и m2 со скоростью порядка v*m3/(m1+m2) полетит влево. В частности, они в ближайшем будущем будут испытывать много-много соударений.
В это время m3 летит к m4, после их соударения улетает обратно — и совсем чуть-чуть варьируя начальные условия, можно добиться, чтобы момент, когда m3 подлетит к m1+m2, был бы опять почти тройным столкновением (точнее, можно сначала подобрать ровно тройное столкновение, а потом сколь угодно слабо от него отступить).
Отступаем совсем чуть-чуть, точку m3 выкидывает "как из пушки" с ещё более огромной скоростью v'>>v, точки m1 и m2 летят влево ещё быстрее, чем раньше, и ещё ближе друг к другу.
m1, m2, m3, m4,
в этом порядке, и пусть m3 в сравнении с остальными очень лёгкая, а в самом начале у m1, m2 и m3 будет почти тройное столкновение, из которого m3 вылетает с огромной скоростью v.
Тогда из-за закона сохранения энергии m1 и m2 остаются очень-очень близко друг к другу — откуда-то ведь нужно было взять эту энергию, а больше неоткуда. А из-за закона сохранения импульса эта "двойная система" из m1 и m2 со скоростью порядка v*m3/(m1+m2) полетит влево. В частности, они в ближайшем будущем будут испытывать много-много соударений.
В это время m3 летит к m4, после их соударения улетает обратно — и совсем чуть-чуть варьируя начальные условия, можно добиться, чтобы момент, когда m3 подлетит к m1+m2, был бы опять почти тройным столкновением (точнее, можно сначала подобрать ровно тройное столкновение, а потом сколь угодно слабо от него отступить).
Отступаем совсем чуть-чуть, точку m3 выкидывает "как из пушки" с ещё более огромной скоростью v'>>v, точки m1 и m2 летят влево ещё быстрее, чем раньше, и ещё ближе друг к другу.
Victor Kleptsyn
22:54
Дальше m3 опять долетает (со своей сумасшедшей скоростью) до m4, отражается (заодно добавив скорости m4), летит обратно, догоняет m1+m2; ещё чуть-чуть варьируя начальные условия, можно подобрать тройное столкновение, и сколь угодно слабо от него отклониться. В результате чего m3 улетит с ещё более безумной (и сколь угодно большой) скоростью v''>>v', и так далее. И раз скорости можно наращивать сколь угодно сильно — можно попросить, чтобы каждый следующий цикл занимал хотя бы в 2 раза меньше времени, чем предыдущий, и тогда вся система "взрывается" за конечное время (привет Ахиллесу и черепахе).
Итог всех этих соударений — m1 и m2 улетели на бесконечность влево, m4 на бесконечность вправо, а у точки m3 просто нет предела (она колеблется всё сильнее и сильнее).
Итог всех этих соударений — m1 и m2 улетели на бесконечность влево, m4 на бесконечность вправо, а у точки m3 просто нет предела (она колеблется всё сильнее и сильнее).
Victor Kleptsyn
М
23:19
Математические байки
Это, конечно, пример вырожденный. Но раз он есть — можно предположить, что пример будет и для настоящих уравнений небесной механики в R^3. И так и есть — и в 1988-м в своей диссертации пример для системы из 5 точек построил Z. Xia (+ статья в Annals!).
Victor Kleptsyn
23:20
Вот тут этот пример схематически изображён:
https://commons.wikimedia.org/wiki/File:Xia%27s_5-body_configuration.png
https://commons.wikimedia.org/wiki/File:Xia%27s_5-body_configuration.png
Victor Kleptsyn
23:31
Система симметрична относительна оси Oz, вдоль которой вверх-вниз движется третья точка; как сверху, так и снизу две "очень сильно эллиптические" двойные системы, в которых точки могут очень-очень сильно сблизиться (и тем самым приблизиться к оси Oz). А дальше (на первом уровне аккуратности) всё почти так же, как и раньше — точка m3 получает сильное ускорение от каждой из этих систем, потому что у неё происходит почти тройное столкновение. А именно, представим себе, что пара m1+m2 сближается сразу за m3, резко её притормаживая и добавляя ей скорость обратно — и разлетается. Работая этаким "ускорителем" (или "ракеткой", или "баскетбольным мячом" в примере выше). Дальше подачу принимает пара m4+m5, отправляет m3 ещё быстрее обратно, и так далее.
Тут нужно отследить, чтобы системы продолжили оставаться "высокоэллиптическими"... Но это уже совсем не тот уровень подробности, в который мне тут хочется углубляться.
Тут нужно отследить, чтобы системы продолжили оставаться "высокоэллиптическими"... Но это уже совсем не тот уровень подробности, в который мне тут хочется углубляться.
Victor Kleptsyn
12 February 2021
М
20:48
Математические байки
In reply to this message
Вот теперь совсем окончание про гипотезу Пенлеве.
Мы уже посмотрели, как сначала в работе Mather и McGehee была предъявлена (мотивирующая то, каким должен быть ответ) вырожденная модель из четырёх точек на прямой, которая, с одной стороны, была пределом небесной механики, а с другой — ломалась не "через столкновение", а так, что предела у траекторий в конечный момент не было — скорости стремились к бесконечности, диаметр системы стремился к бесконечности, часть точек улетала совсем, одна металась туда-сюда. Но эта система ещё была модельной — вырождением настоящей в пределе "точки летают почти по одной прямой, но промахиваются друг мимо друга на бесконечно малую величину".
А потом Z. Xia построил пример начальных условий для уже настоящей системы из пяти материальных точек, в которой решение ломалось без столкновений до последнего момента: две "ракетки"-бинарные системы перекидывают друг другу оставшуюся точку, разгоняя её всё сильнее и сильнее (и сами при этом улетают на бесконечность).
И мне в этом месте по ассоциации вспоминается "линейный магнитный ускоритель" из неодимовых магнитов и шариков (на youtube есть куча видео; вот, например).
И аналогия — причём именно с примером Xia — мне кажется, достаточно хорошая. Потому что что происходит там: точка ускоряется, "упав в потенциальную яму", а потом потенциальная яма резко становится менее глубокой (потому что бинарная система разошлась в стороны от оси), и точка вылетает на (сильно) большей скорости, чем прилетела.
А что происходит в линейном ускорителе? Стальной шарик разгоняется из-за того, что его притягивает магнит. Потом в момент удара его скорость [почти без потерь] передаётся (а-ля колыбель Ньютона) шарику по другую сторону, который дальше и потому в гораздо более мелкой потенциальной яме. Так что после "блока ускорения" шарик имеет большую скорость и энергию, чем до него (правда, шарик уже другой, но такой же).
И даже несколько ускорителей один за другим тут по делу — "ракетки"-бинарные системы же перекидываются мячиком-оставшейся материальной точкой, добавляя ей ещё и ещё скорости и энергии.
Мы уже посмотрели, как сначала в работе Mather и McGehee была предъявлена (мотивирующая то, каким должен быть ответ) вырожденная модель из четырёх точек на прямой, которая, с одной стороны, была пределом небесной механики, а с другой — ломалась не "через столкновение", а так, что предела у траекторий в конечный момент не было — скорости стремились к бесконечности, диаметр системы стремился к бесконечности, часть точек улетала совсем, одна металась туда-сюда. Но эта система ещё была модельной — вырождением настоящей в пределе "точки летают почти по одной прямой, но промахиваются друг мимо друга на бесконечно малую величину".
А потом Z. Xia построил пример начальных условий для уже настоящей системы из пяти материальных точек, в которой решение ломалось без столкновений до последнего момента: две "ракетки"-бинарные системы перекидывают друг другу оставшуюся точку, разгоняя её всё сильнее и сильнее (и сами при этом улетают на бесконечность).
И мне в этом месте по ассоциации вспоминается "линейный магнитный ускоритель" из неодимовых магнитов и шариков (на youtube есть куча видео; вот, например).
И аналогия — причём именно с примером Xia — мне кажется, достаточно хорошая. Потому что что происходит там: точка ускоряется, "упав в потенциальную яму", а потом потенциальная яма резко становится менее глубокой (потому что бинарная система разошлась в стороны от оси), и точка вылетает на (сильно) большей скорости, чем прилетела.
А что происходит в линейном ускорителе? Стальной шарик разгоняется из-за того, что его притягивает магнит. Потом в момент удара его скорость [почти без потерь] передаётся (а-ля колыбель Ньютона) шарику по другую сторону, который дальше и потому в гораздо более мелкой потенциальной яме. Так что после "блока ускорения" шарик имеет большую скорость и энергию, чем до него (правда, шарик уже другой, но такой же).
И даже несколько ускорителей один за другим тут по делу — "ракетки"-бинарные системы же перекидываются мячиком-оставшейся материальной точкой, добавляя ей ещё и ещё скорости и энергии.
Victor Kleptsyn
20:50
Итого — для трёх точечных масс Пенлеве доказал, что уравнение может ломаться только через столкновение точек, для пяти и больше есть пример; оставался собственно случай четырёх тел в без столкновений, как на прямой) варианте.
Оказалось, что для четырёх тел тоже есть пример "разгоняющейся и разлетающейся" системы.
Его построил Jinxin Xue — вот тут их совместная статья с Д. Долгопятом про упрощённую модель, а вот его статья (+препринт 2014 года) с полной конструкцией. И тут потребовалось чуть больше "планетарной хореографии".
Эту конструкцию можно описать как "два Юпитера (Ю1 и Ю2), два астероида (А1 и А2)" — два очень тяжёлых тела, а два очень лёгких (равной массы). В упрощённом варианте тяжёлые тела в пространстве вообще неподвижны — а лёгкие летают между ними туда-сюда.
В любой момент времени один из астероидов обращается вокруг Юпитера Ю2 (по очень низкой орбите, и потому очень быстро), а второй тоже очень быстро летит к Ю1 и обратно (пролетая к нему "почти вплотную"). Когда астероид возвращается, он встречается с тем, который в этот момент обращается вокруг Ю2, пролетая почти вплотную — и они оба (почти как при абсолютно упругом столкновении) меняют свои орбиты.
Оказалось, что для четырёх тел тоже есть пример "разгоняющейся и разлетающейся" системы.
Его построил Jinxin Xue — вот тут их совместная статья с Д. Долгопятом про упрощённую модель, а вот его статья (+препринт 2014 года) с полной конструкцией. И тут потребовалось чуть больше "планетарной хореографии".
Эту конструкцию можно описать как "два Юпитера (Ю1 и Ю2), два астероида (А1 и А2)" — два очень тяжёлых тела, а два очень лёгких (равной массы). В упрощённом варианте тяжёлые тела в пространстве вообще неподвижны — а лёгкие летают между ними туда-сюда.
В любой момент времени один из астероидов обращается вокруг Юпитера Ю2 (по очень низкой орбите, и потому очень быстро), а второй тоже очень быстро летит к Ю1 и обратно (пролетая к нему "почти вплотную"). Когда астероид возвращается, он встречается с тем, который в этот момент обращается вокруг Ю2, пролетая почти вплотную — и они оба (почти как при абсолютно упругом столкновении) меняют свои орбиты.
Victor Kleptsyn
20:53
Вот рисунок из статьи J. Xue, D. Dolgopyat в CMP: тут видно, как происходит прилёт, смена орбит "почти столкновением" и вылет следующего астероида.
(Image credit: Jinxin Xue & Dmitry Dolgopyat, Non-Collision Singularities in the Planar Two-Center-Two-Body Problem, Communications in Mathematical Physics, 345 (2016), pages 797-879)
(Image credit: Jinxin Xue & Dmitry Dolgopyat, Non-Collision Singularities in the Planar Two-Center-Two-Body Problem, Communications in Mathematical Physics, 345 (2016), pages 797-879)
Victor Kleptsyn
20:55
In reply to this message
Честно говоря, при взгляде на эту конструкцию мне вспоминается сцена из "Карамболя" в Пин-коде "Смешариков": "Ну кто так бьёт?!".
Потому что и впрямь, очень-очень близкие пролёты, это же почти что абсолютно упругие столкновения! 🙂
Потому что и впрямь, очень-очень близкие пролёты, это же почти что абсолютно упругие столкновения! 🙂
Victor Kleptsyn
20:55
Кстати (на скриншоте теорема из их же работы) — на каждом шаге можно выбрать, какой из двух астероидов вылетает к Ю1. Поэтому "взрывающихся" решений получается (как минимум) целое канторово множество: столько есть последовательностей из А1 и А2, говорящих, на каком шаге какой астероид летит к Ю1.
Victor Kleptsyn
21:07
В упрощённой модели Юпитеры были "прибиты гвоздями" и не могли двигаться — но почти сразу Xue сделал и совсем честный случай из 4 тел: вот его препринт (первая версия 2014 года), а вот статья в Acta Mathematica, вышедшая в 2020-м. Совсем наши дни!
Victor Kleptsyn
21:07
И на этом я завершаю рассказ про гипотезу Пенлеве.
Victor Kleptsyn
16 February 2021
М
13:52
Математические байки
Да, ещё последняя ссылка про гипотезу Пенлеве: есть хороший популярный текст 1995 года (то есть ещё до конструкции примера с четырьмя точками) — "Off to Infinity in Finite Time" в AMS Notices: https://www.ams.org/notices/199505/saari-2.pdf
А мой следующий большой рассказ будет про степени отображений и теорему Штурма. Но сначала — несколько картинок.
А мой следующий большой рассказ будет про степени отображений и теорему Штурма. Но сначала — несколько картинок.
Victor Kleptsyn
13:52
Во-первых — есть формула для суммы синусов или косинусов от арифметической прогрессии,
sin(a)+sin(a+d)+...+sin(a+n*d)
или
cos(a)+cos(a+d)+...+cos(a+n*d).
Школьными методами проще всего умножить на sin(d/2), после чего каждое произведение разваливается в разность косинусов/синусов, и получается телескопическая сумма, в которой почти всё сокращается.
Можно сказать, что обе эти суммы это мнимая и вещественная части суммы геометрической прогрессии
e^{ia} + e^{i(a+d)} + ... + e^{i(a+n*d)}
со знаменателем e^{id}, и применить формулу для такой суммы.
Получится (если дополнительно поделить числитель и знаменатель на e^{i d/2)} ) выражение
sin(a)+sin(a+d)+...+sin(a+n*d)
или
cos(a)+cos(a+d)+...+cos(a+n*d).
Школьными методами проще всего умножить на sin(d/2), после чего каждое произведение разваливается в разность косинусов/синусов, и получается телескопическая сумма, в которой почти всё сокращается.
Можно сказать, что обе эти суммы это мнимая и вещественная части суммы геометрической прогрессии
e^{ia} + e^{i(a+d)} + ... + e^{i(a+n*d)}
со знаменателем e^{id}, и применить формулу для такой суммы.
Получится (если дополнительно поделить числитель и знаменатель на e^{i d/2)} ) выражение
Victor Kleptsyn
13:53
и вот в знаменателе 2i sin (d/2) и появляется.
Но Полина Вытнова показала мне совершенно классную картинку (отсюда):
Но Полина Вытнова показала мне совершенно классную картинку (отсюда):
Victor Kleptsyn
13:53
Image credit: https://math.stackexchange.com/a/1607308 + https://trigonography.com/2016/01/10/trig-sums-with-angles-in-arithmetic-progression/
Victor Kleptsyn
13:56
Мне кажется, картинка прекрасна — никакого другого текста, кроме уже имеющегося, не надо!
Victor Kleptsyn
17 February 2021
М
17:32
Математические байки
In reply to this message
Второе — в этом канале уже появлялись несколько картинок М. Панова; вот тут коллеги выложили его анимации про параболу/эллипс/гиперболы как огибающие. Так вот, вот здесь с его картинками более развёрнутая презентация с текстом — мне кажется, совершенно потрясающая; я очень советую её пролистать (благо, что это быстро, а рассказ там очень простой и понятный — но не перестающий от этого быть очень красивым!).
Victor Kleptsyn
17:47
In reply to this message
Ну и я напомню, что эллипс/гипербола/парабола как огибающие (серединных) перпендикуляров возникают и в небесной механике!
Victor Kleptsyn
18 February 2021
М
12:01
Математические байки
Н
Непрерывное математическое образование 18.02.2021 11:33:35
https://youtu.be/1LwkljjLBns
https://youtu.be/cp6eudDomRY
https://youtu.be/r_KqR5tBekQ
«««
Soon after winning the Fields Medal in 1962, a young John Milnor gave these now-famous lectures and wrote his timeless Topology from the Differentiable Viewpoint, which has influenced generations of mathematicians. The lectures, filmed by the Mathematical Association of America (MAA), were unavailable for years but recently resurfaced. With Simons Foundation funding, the Mathematical Sciences Research Institute has produced these digital reproductions as a resource for the mathematics and science communities.
(…)
Lectures by John Milnor, Princeton University, Fall term 1958
Notes by James Munkres — https://www.maths.ed.ac.uk/~v1ranick/papers/difftop.pdf
»»»
https://youtu.be/cp6eudDomRY
https://youtu.be/r_KqR5tBekQ
«««
Soon after winning the Fields Medal in 1962, a young John Milnor gave these now-famous lectures and wrote his timeless Topology from the Differentiable Viewpoint, which has influenced generations of mathematicians. The lectures, filmed by the Mathematical Association of America (MAA), were unavailable for years but recently resurfaced. With Simons Foundation funding, the Mathematical Sciences Research Institute has produced these digital reproductions as a resource for the mathematics and science communities.
(…)
Lectures by John Milnor, Princeton University, Fall term 1958
Notes by James Munkres — https://www.maths.ed.ac.uk/~v1ranick/papers/difftop.pdf
»»»
Victor Kleptsyn
12:01
Н
Непрерывное математическое образование 18.02.2021 11:35:00
http://www.ams.org/notices/201106/rtx110600804p.pdf
«The sequel to these lectures, written several mathematical lives — and a Wolf and an Abel Prize later — is “Differential Topology Forty-six Years Later”»
«The sequel to these lectures, written several mathematical lives — and a Wolf and an Abel Prize later — is “Differential Topology Forty-six Years Later”»
Victor Kleptsyn
М
13:51
Математические байки
In reply to this message
Пара кадров из первой лекции. Вообще, очень интересно смотреть и слушать (в том числе — пойманный "дух эпохи").
Victor Kleptsyn
22 February 2021
М
16:07
Математические байки
Давайте я начну обещанный рассказ про степени отображений и про теорему Штурма.
Вот допустим, нам задан какой-нибудь многочлен. С явными — целыми или рациональными — коэффициентами, но не второй-третьей-ну допустим, четвёртой степени, а выше, так что никакой формулы для корней нет. Как можно узнать, сколько у него вещественных корней? Или — сколько у него корней на конкретном отрезке [a,b]?
Собственно, вот конкретный пример: рассмотрим многочлен
P(x) = 2 x^5 - 5 x^4 - 4 x^3 + 22 x^2 - 21 x + 6.
Сколько у него вещественных корней?
Так сразу не скажешь. Даже если построить график — точнее, попросить компьютер это сделать — тоже ответ не то, чтобы сразу очевиден:
Вот допустим, нам задан какой-нибудь многочлен. С явными — целыми или рациональными — коэффициентами, но не второй-третьей-ну допустим, четвёртой степени, а выше, так что никакой формулы для корней нет. Как можно узнать, сколько у него вещественных корней? Или — сколько у него корней на конкретном отрезке [a,b]?
Собственно, вот конкретный пример: рассмотрим многочлен
P(x) = 2 x^5 - 5 x^4 - 4 x^3 + 22 x^2 - 21 x + 6.
Сколько у него вещественных корней?
Так сразу не скажешь. Даже если построить график — точнее, попросить компьютер это сделать — тоже ответ не то, чтобы сразу очевиден:
Victor Kleptsyn
16:07
Похоже, конечно, что корней три — а может, всё-таки пять, если где-то между 0 и 1.5 корней будет четыре, а не два?
Если сильно увеличить — то становится видно, что корней на том интервале всё-таки два (а всего тем самым три):
Если сильно увеличить — то становится видно, что корней на том интервале всё-таки два (а всего тем самым три):
Victor Kleptsyn
16:13
Но, скажем, если представить себе прописывание алгоритма для компьютера — то станет немного тоскливо. Потому что надо — выбрать мелкую сетку значений, посмотреть, сколько между ними перемен знака, проконтролировать, знаем ли мы, что на тех отрезках, где перемены знака нет, многочлен с разумной оценкой на производную (или на вторую производную) "не успевает" добежать до нуля и вернуться. А если может успеть — то подразбить интервал на более мелкие шаги, и так повторять "до победы".
И, кстати, на тех, где есть — тоже нужно быть уверенными, что там корень один, а не, скажем, три.
(И я тут ещё пропустил начальный шаг — проверку через алгоритма Евклида для вычисления НОД(P,P'), что у многочлена нет кратных корней; а если вдруг есть — то ещё и это нужно обрабатывать...)
Не то, чтобы написать было совсем неподъёмно — но как-то никакого энтузиазма не возникает. А главное, в таком виде это не получится "подружить" с разными другими применениями из алгебраической геометрии... (Забегая вперёд — с образами полуалгебраических множеств и теоремой об элиминации кванторов.)
И, кстати, на тех, где есть — тоже нужно быть уверенными, что там корень один, а не, скажем, три.
(И я тут ещё пропустил начальный шаг — проверку через алгоритма Евклида для вычисления НОД(P,P'), что у многочлена нет кратных корней; а если вдруг есть — то ещё и это нужно обрабатывать...)
Не то, чтобы написать было совсем неподъёмно — но как-то никакого энтузиазма не возникает. А главное, в таком виде это не получится "подружить" с разными другими применениями из алгебраической геометрии... (Забегая вперёд — с образами полуалгебраических множеств и теоремой об элиминации кванторов.)
Victor Kleptsyn
16:15
Так вот — а нет ли какого-нибудь красивого способа это самое число вещественных корней найти? Оказывается, что есть, и именно это и есть теорема Штурма; и мы на неё сейчас посмотрим — с чуть более топологической точки зрения, чем её обычно рассказывают.
Victor Kleptsyn
16:24
Но сначала — мне понадобится понятие степени отображения.
В простейшем варианте — если у нас есть отображение f:S^1\to S^1 из окружности в окружность, то можно спросить, какое число оборотов (с учётом знака) делает f(x) вдоль окружности-образа, когда x один раз пробегает окружность-прообраз. Это и есть степень deg f.
И как всегда, с ней есть общий принцип из топологии: "если что-то меняется непрерывно и принимает целые значения, то эта величина — константа". В данном случае — степень сохраняется, если отображение f непрерывно менять.
В простейшем варианте — если у нас есть отображение f:S^1\to S^1 из окружности в окружность, то можно спросить, какое число оборотов (с учётом знака) делает f(x) вдоль окружности-образа, когда x один раз пробегает окружность-прообраз. Это и есть степень deg f.
И как всегда, с ней есть общий принцип из топологии: "если что-то меняется непрерывно и принимает целые значения, то эта величина — константа". В данном случае — степень сохраняется, если отображение f непрерывно менять.
Victor Kleptsyn
16:30
Представьте себе теперь, что вдоль круглого стадиона бежит атлет. А мы должны сказать, сколько кругов он сделал. Понятно, что бежать за ним весьма трудозатратно; гораздо проще встать в одной точке и считать, сколько раз он мимо нас пробежал.
Но считать надо с учётом знака, по или против хода он мимо нас движется. Потому что если атлет пробежит мимо нас, остановится, сделает пять шагов назад, пройдя мимо нас второй раз, а потом побежит опять вперёд, пройдя третий раз, то не надо говорить, что он уже сделал три круга (иначе остальные бегуны могут сильно удивиться).
Но считать надо с учётом знака, по или против хода он мимо нас движется. Потому что если атлет пробежит мимо нас, остановится, сделает пять шагов назад, пройдя мимо нас второй раз, а потом побежит опять вперёд, пройдя третий раз, то не надо говорить, что он уже сделал три круга (иначе остальные бегуны могут сильно удивиться).
Victor Kleptsyn
16:31
А с учётом знака всё получается правильно. А именно — если f:S^1\to S^1 это гладкое отображение, а точка p такова, что во всех её прообразах производная f ненулевая (в частности, таких прообразов тогда конечное число), то
deg(f) = \sum_{x: f(x)=p} sign f'(x).
deg(f) = \sum_{x: f(x)=p} sign f'(x).
Victor Kleptsyn
16:35
Вот, например, отображение степени 2. У отмеченной на оси ординат точки 4 прообраза, в трёх из них f'>0, в одной f'<0, поэтому степень равна
1+1-1+1=2.
Кстати, у точки, которой отвечает начало отрезка на оси ординат (склеенное с концом этого же отрезка — это же окружность), два прообраза, оба с плюсом. И мы опять получаем 1+1=2 — что логично: мы же находим одну и ту же величину deg f, которую уже определили как "число оборотов".
1+1-1+1=2.
Кстати, у точки, которой отвечает начало отрезка на оси ординат (склеенное с концом этого же отрезка — это же окружность), два прообраза, оба с плюсом. И мы опять получаем 1+1=2 — что логично: мы же находим одну и ту же величину deg f, которую уже определили как "число оборотов".
Victor Kleptsyn
М
17:33
Математические байки
In reply to this message
С другой стороны, я мог бы не говорить про "число оборотов", а сразу определить степень как число прообразов с учётом знака. И тогда была бы нужна "проверка корректности": во-первых, почему такая точка p есть (у которой все прообразы с ненулевой производной), а во-вторых, почему две разные точки будут приводить к одному и тому же результату.
И тогда для первой части корректности нужно было бы сказать, что множество тех p, у которых хотя бы в одном прообразе производная f нулевая — иными словами, множество критических значений f — имеет меру ноль.
В некоторых кавычках — потому что его мера оценивается сверху интегралом от |f'| по множеству критических точек — но интегрируем-то мы ноль!
А чуть более аккуратно — покрываем множество критических точек маленькими интервалами с суммой длин, близкой к его мере; когда мы применяем f — длина образа каждого интервала оценивается по теореме Лагранжа, как длина самого интервала * что-то очень маленькое (потому что где-то там f'=0). Так что сумма длин образов оказывается сколь угодно малой — и вот и мера ноль.
И тогда для первой части корректности нужно было бы сказать, что множество тех p, у которых хотя бы в одном прообразе производная f нулевая — иными словами, множество критических значений f — имеет меру ноль.
В некоторых кавычках — потому что его мера оценивается сверху интегралом от |f'| по множеству критических точек — но интегрируем-то мы ноль!
А чуть более аккуратно — покрываем множество критических точек маленькими интервалами с суммой длин, близкой к его мере; когда мы применяем f — длина образа каждого интервала оценивается по теореме Лагранжа, как длина самого интервала * что-то очень маленькое (потому что где-то там f'=0). Так что сумма длин образов оказывается сколь угодно малой — и вот и мера ноль.
Victor Kleptsyn
17:37
А для второй (для совпадения того, что дадут две разные точки p_1 и p_2) — чуть-чуть возмутить f, чтобы прообразы p_1 и p_2 остались почти такими же (в частности — с теми же знаками производной), но все минимумы и максимумы у f стали бы невырожденными и на разных уровнях. И тогда, когда мы "поведём" точку p от p_1 к p_2, всё, что мы будем наблюдать, это как два прообраза с разными знаками производной сливаются и исчезают — или, наоборот, из пустоты появляются два прообраза с разными знаками. И при этом наша сумма не изменяется.
Victor Kleptsyn
М
18:17
Математические байки
In reply to this message
И вот это определение обобщается сразу на любую размерность. А именно: пусть у нас есть два ориентированных (ориентация уже выбрана) замкнутых (компактных без края) гладких многообразия M и N одной размерности, и гладкое отображение f:M\to N. Тогда степень deg f отображения f определяется так:
- берём точку p на N, у которой для каждого её прообраза x дифференциал df|_x (линейная часть f в точке x) невырожден.
- для каждого её прообраза пишем +1 или -1 в зависимости от того, сохраняет или меняет f рядом с ним ориентацию (иными словами, пишем sign det df|_x)
- складываем всё, что написано.
Опять же, нужна проверка корректности: что такая точка p есть, и что результат не зависит от её выбора. Первое делается аналогично тому, что мы делали на окружности, только с поправкой на многомерность, и называется леммой Сарда : множество критических значений (достаточно) гладкой функции имеет меру ноль.
- берём точку p на N, у которой для каждого её прообраза x дифференциал df|_x (линейная часть f в точке x) невырожден.
- для каждого её прообраза пишем +1 или -1 в зависимости от того, сохраняет или меняет f рядом с ним ориентацию (иными словами, пишем sign det df|_x)
- складываем всё, что написано.
Опять же, нужна проверка корректности: что такая точка p есть, и что результат не зависит от её выбора. Первое делается аналогично тому, что мы делали на окружности, только с поправкой на многомерность, и называется леммой Сарда : множество критических значений (достаточно) гладкой функции имеет меру ноль.
Victor Kleptsyn
М
18:52
Математические байки
И вторая часть тоже проверяется более-менее так же как и для окружности: соединить две точки p_1 и p_2 типичным путём и если надо, чуть-чуть пошевелить отображение f. Тогда при движении от p_1 к p_2 по типичному пути для типичной f всё, что нам может встретиться, это "вырождения коразмерности 1". А это только слияние двух прообразов с разным сохранением-изменением ориентации и их исчезновение (или, наоборот, рождение двух с разными знаками из ничего).
Victor Kleptsyn
27 February 2021
М
14:23
Математические байки
М
Математические этюды 27.02.2021 14:16:35
Сегодняшние мультфильмы от Миши Панова демонстрируют некоторые разрезания куба на равные многогранники. Попробуйте разрезать куб на 3 равных тетраэдра. А на 6? Кстати, в случае трёх частей можно не ограничиваться тетраэдрами: второй и третий мультфильмы показывают целое множество разрезаний на три равных многогранника.
Victor Kleptsyn
7 March 2021
М
20:40
Математические байки
In reply to this message
Продолжим?
Для начала — мне хотелось показать две картинки из "Теории катастроф" В.И. Арнольда. Первая — показывает складку при проекции сферы, и чуть более сложную особенность ("сборку") — но собственно эта особенность происходит над одной точкой (то есть над коразмерностью два) — а если какой-нибудь путь внизу не проходит прямо через неё (чего всегда можно добиться малым шевелением), то всё, что на этом пути мы встретим, будут только точки склейки. Вот она:
Для начала — мне хотелось показать две картинки из "Теории катастроф" В.И. Арнольда. Первая — показывает складку при проекции сферы, и чуть более сложную особенность ("сборку") — но собственно эта особенность происходит над одной точкой (то есть над коразмерностью два) — а если какой-нибудь путь внизу не проходит прямо через неё (чего всегда можно добиться малым шевелением), то всё, что на этом пути мы встретим, будут только точки склейки. Вот она:
Victor Kleptsyn
20:42
Вторая же показывает, почему тор правильно рисовать так, как его рисуют. (До сих пор помню, как меня на первом курсе НМУ этому научили!)
Дело в том, что если нарисовать тор от руки как "эллипс, а внутри эллипс, изображающий дырку", то это будет восприниматься скорее как кольцо, чем как трёхмерный объект (и к тому есть причина):
Дело в том, что если нарисовать тор от руки как "эллипс, а внутри эллипс, изображающий дырку", то это будет восприниматься скорее как кольцо, чем как трёхмерный объект (и к тому есть причина):
Victor Kleptsyn
20:43
Чтобы картинка воспринималась, как тор, вырезаемую дырку нужно нарисовать двумя дугами — причём одну из них более длинной, а другую остановить при пересечении с первой:
Victor Kleptsyn
20:52
In reply to this message
Так вот — эта картинка действительно более правильна с геометрической точки зрения. А именно — возьмём тор в R^3, и спроецируем его на "плоскость зрения" немного под углом. Отметим те его точки, где касательная к нему плоскость параллельна направлению проекцирования — иначе говоря, как раз критические точки проекции.
Victor Kleptsyn
20:53
In reply to this message
В их образе мы увидим как раз вот эту кривую — и у неё будет ещё "невидимая" компонента, которая при настоящем взгляде оказывается закрыта другой частью тора. И вот вторая картинка:
Victor Kleptsyn
21:07
In reply to this message
Кстати, особенность, которая получается в проекции этой кривой — это касп. Тот самый касп, который мы пересекаем при первом преобразовании Рейдемейстера диаграммы узла: если в проекции узла есть петелька, и её "вытягиванием" убрать, то в тот момент, когда она вырождается, в одной из точек узла направление касательной совпадает с направлением проекции, и мы видим полукубическую "точку возврата":
Victor Kleptsyn
21:18
Но давайте вернёмся к степеням отображений окружности и к теореме Штурма — а то я до неё и в этот раз не доберусь.
Итак, у нас написан явно вещественный многочлен (для простоты, без кратных корней) — и мы хотим найти, сколько у него вещественных корней.
Если добавить к вещественной прямой бесконечно удалённую точку, то получается окружность. И многочлен (доопределённый бесконечностью в бесконечности) это непрерывное отображение такой окружности в себя. А корни это прообразы нуля, и очень бы хотелось применить как раз науку о степени.
Итак, у нас написан явно вещественный многочлен (для простоты, без кратных корней) — и мы хотим найти, сколько у него вещественных корней.
Если добавить к вещественной прямой бесконечно удалённую точку, то получается окружность. И многочлен (доопределённый бесконечностью в бесконечности) это непрерывное отображение такой окружности в себя. А корни это прообразы нуля, и очень бы хотелось применить как раз науку о степени.
Victor Kleptsyn
21:20
In reply to this message
Увы, буквально так это сделать не получается: корни идут, чередуясь, то с положительной, то с отрицательной производной, и в определении степени у нас то плюс, то минус единицы, и почти (или совсем) всё сокращается.
Victor Kleptsyn
21:22
А именно — топологическая (приходится уточнять!) степень многочлена чётной (алгебраической) степени равна нулю (тут сокращается всё — а ещё можно сказать, что либо больших положительных, либо больших отрицательных значений он не принимает), а топологическая степень многочлена нечётной алгебраической степени это +1 или -1, в зависимости от знака старшего коэффициента.
Victor Kleptsyn
21:23
Казалось бы, тупик?
Victor Kleptsyn
21:24
Но — раз нам помешала производная, так она же нам и поможет! Давайте на неё поделим — рассмотрим рациональную функцию
R(x)=P(x)/P'(x)
R(x)=P(x)/P'(x)
Victor Kleptsyn
21:27
Заметим, что корни — прообразы нуля — у неё те же, что и у самого многочлена P. Зато производная в каждой из этих точек просто равна 1! (Потому что в каждом корне x_0, раз он некратный, P'(x_0) не обращается в ноль, а тогда рядом с ним мы P(x)~P'(x_0)*(x-x_0) почти что на эту константу поделили — вот производная и стала единичной.)
Victor Kleptsyn
21:29
Значит, если мы будем искать топологическая степень R(x)=P(x)/P'(x) через прообразы нуля — все они войдут со знаком "плюс". И мы и получили желаемое (на всякий случай — помните, что P без кратных корней):
Victor Kleptsyn
21:31
Это пол-пути: мы свели исходный вопрос "сколько корней у P" к топологическому вопросу: "а чему равна топологическая степень заданной рациональной функции?".
Осталось на этот вопрос научиться отвечать!
Осталось на этот вопрос научиться отвечать!
Victor Kleptsyn
М
21:56
Математические байки
На самом деле — мы научимся находить топологическую степень любой рациональной функции R(x)=P_1(x)/P_2(x). Для этого, если
deg_{alg} P_1 >= deg_{alg} P_2
(иными словами, если дробь неправильная), то выделим из неё главную часть: поделим P_1 на P_2 с остатком. Пусть
P_1=Q*P_2 + S, где S — остаток:
deg_{alg} S < deg_{alg} P_2.
Тогда
P_1/P_2 = Q + (S/P_2).
deg_{alg} P_1 >= deg_{alg} P_2
(иными словами, если дробь неправильная), то выделим из неё главную часть: поделим P_1 на P_2 с остатком. Пусть
P_1=Q*P_2 + S, где S — остаток:
deg_{alg} S < deg_{alg} P_2.
Тогда
P_1/P_2 = Q + (S/P_2).
Victor Kleptsyn
21:57
А теперь (вместо нуля, как раньше) посмотрим на прообразы бесконечности (ну или, если она окажется критическим значением, на прообразы чего-нибудь очень большого).
Victor Kleptsyn
22:02
Сумма
Q + (S/ P_2)
обращается в бесконечность либо в бесконечности — из-за Q — либо там, где обращается в ноль знаменатель. Но в первом случае она ведёт себя "топологически неотличимо" от Q (потому что отношение S/P_2 там маленькое), а во втором — от S/P_2 (потому что Q там это почти константа, где ей тягаться с бесконечностью).
Поэтому мы просто считаем всё по отдельности: топологическая степень исходной дроби P_1/P_2 равна сумме топологической степени её главной части — многочлена Q — и топологической степени S/P_2.
Q + (S/ P_2)
обращается в бесконечность либо в бесконечности — из-за Q — либо там, где обращается в ноль знаменатель. Но в первом случае она ведёт себя "топологически неотличимо" от Q (потому что отношение S/P_2 там маленькое), а во втором — от S/P_2 (потому что Q там это почти константа, где ей тягаться с бесконечностью).
Поэтому мы просто считаем всё по отдельности: топологическая степень исходной дроби P_1/P_2 равна сумме топологической степени её главной части — многочлена Q — и топологической степени S/P_2.
Victor Kleptsyn
22:05
In reply to this message
Причём топологическую степень Q — как степень многочлена — мы уже знаем (и уже нашли в ходе первой попытки!).
Victor Kleptsyn
22:07
Итак, один раз можно поделить с остатком, и степень числителя уменьшится. А что делать дальше?
Да просто перевернуть дробь! Точнее, (1/y), как и (-y) — изменяющие ориентацию гомеоморфизмы окружности, поэтому они знак степени поменяют. Не сильно страшно, но неприятно. Зато если взять их композицию, (-1/y), то вот она ориентацию сохраняет (кстати, если вещественную прямую отобразить на окружность стереографической проекцией, то на ней это центральная симметрия — иными словами, поворот на 180 градусов). И поэтому для любой рациональной функции R_1 выполнено
deg_{top} R_1 = deg_{top} -1/R_1.
Да просто перевернуть дробь! Точнее, (1/y), как и (-y) — изменяющие ориентацию гомеоморфизмы окружности, поэтому они знак степени поменяют. Не сильно страшно, но неприятно. Зато если взять их композицию, (-1/y), то вот она ориентацию сохраняет (кстати, если вещественную прямую отобразить на окружность стереографической проекцией, то на ней это центральная симметрия — иными словами, поворот на 180 градусов). И поэтому для любой рациональной функции R_1 выполнено
deg_{top} R_1 = deg_{top} -1/R_1.
Victor Kleptsyn
22:12
Обозначим P_3=-S — минус остаток, и тогда
deg_{top} S/P_2 = deg_{top} -P_2/S = deg_{top} P_2/P_3.
И вот у нас опять неправильная дробь. Можно опять поделить с остатком, опять перевернуть, и так далее — пока мы не дойдём до константы (у которой, естественно, будет нулевая степень).
deg_{top} S/P_2 = deg_{top} -P_2/S = deg_{top} P_2/P_3.
И вот у нас опять неправильная дробь. Можно опять поделить с остатком, опять перевернуть, и так далее — пока мы не дойдём до константы (у которой, естественно, будет нулевая степень).
Victor Kleptsyn
22:15
А если посмотреть на то, что мы делаем — то это можно назвать либо алгоритмом Евклида (с минимальной поправкой на знаки), либо — разложением в цепную дробь Хирцебруха (то есть цепную дробь "с минусами"),
P_1/P_2 = Q_1 - 1/(Q_2 - 1/( Q_3 - ... ))
P_1/P_2 = Q_1 - 1/(Q_2 - 1/( Q_3 - ... ))
Victor Kleptsyn
22:16
И искомая топологическая степень R это просто сумма топологических степеней неполных частных Q_j:
Victor Kleptsyn
22:18
А — повторюсь, топологические степени Q_j мы знаем: это 0, если степень deg_{alg} Q_j чётна, и знак старшего коэффициента Q_j, если степень deg_{alg} Q_j нечётна.
Victor Kleptsyn
22:21
Так что — мы уже получили алгоритм, который можно применять, совсем не думая. Запускаем алгоритм Евклида (с модификацией знаков), смотрим, какие неполные частные получаются, на их топологические степени, складываем — и получаем искомое число вещественных нулей P.
Victor Kleptsyn
22:30
А что, если мы захотим найти число корней не на всей прямой, а только на каком-нибудь отрезке [a,b]? (Пусть для простоты a и b не являются корнями — в конце концов, конкретные точки можно явно подставить и проверить.)
Во-первых, мы уже знаем достаточно, чтобы выкрутиться. А именно — можно найти просто число корней, меньших b — и так же найти число корней, меньших a, а потом вычесть одно из другого. Теперь, мы возьмём всё то же самое отношение P/P', но поделим его ещё на (x-b), то корни останутся теми же, но большие b будут считаться "с плюсом", а меньшие b — "с минусом".
Так что топологическая степень P/((x-b)*P') равна разности числа корней, больших и меньших b. Знаем сумму (общее число вещественных корней) и знаем разность — значит, знаем по отдельности, сколько корней, меньших b, а сколько больших.
Во-первых, мы уже знаем достаточно, чтобы выкрутиться. А именно — можно найти просто число корней, меньших b — и так же найти число корней, меньших a, а потом вычесть одно из другого. Теперь, мы возьмём всё то же самое отношение P/P', но поделим его ещё на (x-b), то корни останутся теми же, но большие b будут считаться "с плюсом", а меньшие b — "с минусом".
Так что топологическая степень P/((x-b)*P') равна разности числа корней, больших и меньших b. Знаем сумму (общее число вещественных корней) и знаем разность — значит, знаем по отдельности, сколько корней, меньших b, а сколько больших.
Victor Kleptsyn
22:33
Но это не очень смотрится. И действительно, можно сделать сильно красивее — и при этом получится более известная формулировка теоремы Штурма про количество перемен знака и разность между ними в точках b и a. А для этого нам потребуется выйти на плоскость — но это я сделаю в следующий раз; а на сегодня я прекращаю дозволенные речи.
Victor Kleptsyn
12 March 2021
М
19:16
Математические байки
Пока я закопался в делах и судорожно заполняю разные бумаги — пара ссылок/кросспостов:
Victor Kleptsyn
М
19:17
Математические байки
t
tropical saint petersburg 12.03.2021 00:21:41
Тройки Маркова — целые решения уравнения на картинке — появляются везде. Например, теорема Гурвича говорит, что у любого вещественного числа есть хорошие приближения рациональными — с константовй sqrt 5. Такая константа только для ф— золотого сечения. Если выкинуть все числа типа (mф+n)/(kф+l) — то константа для остального будет sqrt 8. И так далее. Эти константы (числа Лагранжа) выражаются через числа Маркова.
Ещё красивее: вещественные точки на кубике x^2+y^2+z^2=xyz параметризуют все гиперболические структуры (конечного объёма) на проколотом торе. А целые точки на кубике (утроенные числа Маркова по сути) параметризуют такие проколотые торы, что длины (всех!) геодезических на них — это в точности (все) числа Маркова. Поэтому вместо чисел Маркова можно изучать геометрию проколотого тора.
Подробности — в ссылках из короткой статьи. Придумали это независимо (и давно) Cohn и Горшков.
Ещё красивее: вещественные точки на кубике x^2+y^2+z^2=xyz параметризуют все гиперболические структуры (конечного объёма) на проколотом торе. А целые точки на кубике (утроенные числа Маркова по сути) параметризуют такие проколотые торы, что длины (всех!) геодезических на них — это в точности (все) числа Маркова. Поэтому вместо чисел Маркова можно изучать геометрию проколотого тора.
Подробности — в ссылках из короткой статьи. Придумали это независимо (и давно) Cohn и Горшков.
Victor Kleptsyn
М
19:18
Математические байки
А ещё про марковские тройки была замечательная (но сложная) лекция Веселова в ЛШСМ-2017: http://www.mathnet.ru/php/presentation.phtml?option_lang=rus&presentid=17717
Victor Kleptsyn
М
19:35
Математические байки
А про взгляд на кубику
x^2+y^2+z^2-xyz=d
с точки зрения SL(2,R)-матриц (и при чём тут квазипериодичность) я расскажу как-нибудь в другой раз, потому что не хочу врать в коэффициентах и знаках...
Несколько соседних ключевых слов — кубика Кэли, trace map; пара ссылок —
А. Городецкий, D. Damanik, Hyperbolicity of the Trace Map for the Weakly Coupled Fibonacci Hamiltonian;
S. Cantat, Bers and Hénon, Painlevé and Schrödinger.
x^2+y^2+z^2-xyz=d
с точки зрения SL(2,R)-матриц (и при чём тут квазипериодичность) я расскажу как-нибудь в другой раз, потому что не хочу врать в коэффициентах и знаках...
Несколько соседних ключевых слов — кубика Кэли, trace map; пара ссылок —
А. Городецкий, D. Damanik, Hyperbolicity of the Trace Map for the Weakly Coupled Fibonacci Hamiltonian;
S. Cantat, Bers and Hénon, Painlevé and Schrödinger.
Victor Kleptsyn
М
19:50
Математические байки
===
А ещё тут нашли третье представление тройки в виде трёх кубов целых чисел. Одно очевидное (1+1+1=3), второе уже выходит в отрицательные числа (но его найти это ещё простое упражнение), а вот третье нашли только что (улучшив алгоритм поиска).
Текст N+1: https://nplus1.ru/news/2021/03/12/diophantine-equation
Непрерывное математическое образование: https://t.me/cme_channel/2140
А ещё тут нашли третье представление тройки в виде трёх кубов целых чисел. Одно очевидное (1+1+1=3), второе уже выходит в отрицательные числа (но его найти это ещё простое упражнение), а вот третье нашли только что (улучшив алгоритм поиска).
Текст N+1: https://nplus1.ru/news/2021/03/12/diophantine-equation
Непрерывное математическое образование: https://t.me/cme_channel/2140
Victor Kleptsyn
19:53
===
Victor Kleptsyn
19:54
(И на этом я убежал писать бумаги дальше)
Victor Kleptsyn
14 March 2021
М
12:17
Математические байки
Продолжим?
Вот мы, применяя алгоритм Евклида, получили последовательность P_j, начинающуюся с наших P_1=P и P_2=P' (ну или абы каких P_1 и P_2, если мы ищем топологическую степень произвольной рациональной функции R=P_1/P_2). И её можно определить вот такой цепочкой:
P_1+P_3 = P_2 * Q_1,
P_2+P_4 = P_3 * Q_2,
P_3+P_5 = P_4 * Q_3,
...
и заканчивается она на каком-то P_k=const, и P_{k+1}=0.
Давайте для каждой точки x рассмотрим последовательность значений P_1(x), P_2(x), ..., P_k(x),
и обозначим через N(x) число перемен знака в этой последовательности: сколько раз + меняется на - и наоборот.
Классический способ формулировать теорему Штурма — как раз в терминах числа перемен знака:
Теорема Штурма. Пусть P — многочлен без кратных корней, не обращающийся в ноль в точках a и b. Тогда число корней P на отрезке [a,b] равно N(a)-N(b).
(А полное число вещественных корней это N(-\infty)-N(\infty), благо что знак полинома на плюс-минус бесконечности определить не проблема.)
Пример: возьмём P(x)=x^2-1. Тогда P'(x)=2x, и мы получаем последовательность
P_1=x^2-1,
P_2=2x,
P_3=1 (помните про смену знака у остатка!).
Последовательность знаков в разных точках и число перемен знака:
-\infty: +,-,+; 2 перемены;
-2: +,-,+; 2 перемены;
-0.5: -,-,+; 1 перемена;
-0.1: -,-,+; 1 перемена;
0.1: -,+,+; 1 перемена;
1.5: +,+,+; 0 перемен;
\infty: +,+,+; 0 перемен.
Уже из бесконечностей мы видим, что число перемен знака меняется между +\infty и -\infty на 2, так что у многочлена x^2-1 два вещественных корня. Более того, такое же число перемен знака между -2 и 1.5, так что они живут на этом отрезке. Причём один из них живёт на отрезке [-2,-0.5], а второй на отрезке [0.1,1.5]. Большой прогресс!
Но если серьёзно — мы только что научились алгоритмически (и довольно просто!) искать (с любой нужной точностью) все корни вещественного многочлена. Начинаем с какого-нибудь отрезка, на котором они гарантированно все лежат (за пределами которого старший член a_n*x^n превышает по модулю сумму модулей всех остальных), а потом запускаем деление пополам, последовательно деля каждый отрезок, на котором число перемен знака меняется.
Осталось
а) доказать;
б) понять, как этот подход "склеивается" с предыдущим.
Вот мы, применяя алгоритм Евклида, получили последовательность P_j, начинающуюся с наших P_1=P и P_2=P' (ну или абы каких P_1 и P_2, если мы ищем топологическую степень произвольной рациональной функции R=P_1/P_2). И её можно определить вот такой цепочкой:
P_1+P_3 = P_2 * Q_1,
P_2+P_4 = P_3 * Q_2,
P_3+P_5 = P_4 * Q_3,
...
и заканчивается она на каком-то P_k=const, и P_{k+1}=0.
Давайте для каждой точки x рассмотрим последовательность значений P_1(x), P_2(x), ..., P_k(x),
и обозначим через N(x) число перемен знака в этой последовательности: сколько раз + меняется на - и наоборот.
Классический способ формулировать теорему Штурма — как раз в терминах числа перемен знака:
Теорема Штурма. Пусть P — многочлен без кратных корней, не обращающийся в ноль в точках a и b. Тогда число корней P на отрезке [a,b] равно N(a)-N(b).
(А полное число вещественных корней это N(-\infty)-N(\infty), благо что знак полинома на плюс-минус бесконечности определить не проблема.)
Пример: возьмём P(x)=x^2-1. Тогда P'(x)=2x, и мы получаем последовательность
P_1=x^2-1,
P_2=2x,
P_3=1 (помните про смену знака у остатка!).
Последовательность знаков в разных точках и число перемен знака:
-\infty: +,-,+; 2 перемены;
-2: +,-,+; 2 перемены;
-0.5: -,-,+; 1 перемена;
-0.1: -,-,+; 1 перемена;
0.1: -,+,+; 1 перемена;
1.5: +,+,+; 0 перемен;
\infty: +,+,+; 0 перемен.
Уже из бесконечностей мы видим, что число перемен знака меняется между +\infty и -\infty на 2, так что у многочлена x^2-1 два вещественных корня. Более того, такое же число перемен знака между -2 и 1.5, так что они живут на этом отрезке. Причём один из них живёт на отрезке [-2,-0.5], а второй на отрезке [0.1,1.5]. Большой прогресс!
Но если серьёзно — мы только что научились алгоритмически (и довольно просто!) искать (с любой нужной точностью) все корни вещественного многочлена. Начинаем с какого-нибудь отрезка, на котором они гарантированно все лежат (за пределами которого старший член a_n*x^n превышает по модулю сумму модулей всех остальных), а потом запускаем деление пополам, последовательно деля каждый отрезок, на котором число перемен знака меняется.
Осталось
а) доказать;
б) понять, как этот подход "склеивается" с предыдущим.
Victor Kleptsyn
15 March 2021
М
12:54
Математические байки
К прошедшему вчера Pi Day хочется вспомнить несколько видео: три видео 3Blue1Brown,
*) https://www.youtube.com/watch?v=d-o3eB9sfls — очень классное доказательство формулы для суммы обратных квадратов, где окружность с расставленными на ней маяками появляется явно;
*) https://www.youtube.com/watch?v=8GPy_UMV-08 — а это формула Валлиса (произведение 2/1 * 2/3 * 4/3 * 4/5 * ... = π/2); опять окружность, выход в комплексные числа, многочлены, произведение расстояний — и всё получается;
*) https://www.youtube.com/watch?v=NaL_Cb42WyY — как связать сумму
1 - 1/3 + 1/5 - 1/7 + ... = π/4
с окружностью (спойлер: никакого Тейлора и арктангенса! Разложение чисел в сумму квадратов, характеры, подсчёт числа целых точек).
И рождественскую лекцию Дональда Кнута в Стенфорде, "Why Pi":
https://www.youtube.com/watch?v=cI6tt9QfRdo (которая, на самом деле, заслуживает отдельного пересказа).
*) https://www.youtube.com/watch?v=d-o3eB9sfls — очень классное доказательство формулы для суммы обратных квадратов, где окружность с расставленными на ней маяками появляется явно;
*) https://www.youtube.com/watch?v=8GPy_UMV-08 — а это формула Валлиса (произведение 2/1 * 2/3 * 4/3 * 4/5 * ... = π/2); опять окружность, выход в комплексные числа, многочлены, произведение расстояний — и всё получается;
*) https://www.youtube.com/watch?v=NaL_Cb42WyY — как связать сумму
1 - 1/3 + 1/5 - 1/7 + ... = π/4
с окружностью (спойлер: никакого Тейлора и арктангенса! Разложение чисел в сумму квадратов, характеры, подсчёт числа целых точек).
И рождественскую лекцию Дональда Кнута в Стенфорде, "Why Pi":
https://www.youtube.com/watch?v=cI6tt9QfRdo (которая, на самом деле, заслуживает отдельного пересказа).
Victor Kleptsyn
М
12:55
Математические байки
Н
Непрерывное математическое образование 22.03.2019 11:09:56
а про формулу Валлиса для π и про появление π в комбинаторике лет 10 назад интересно рассказывал Д.Кнут — можно посмотреть видео или почитать конспект
Victor Kleptsyn
М
13:02
Математические байки
И калейдоскоп тоже очень хорош!
Victor Kleptsyn
М
13:02
Математические байки
Н
Непрерывное математическое образование 14.03.2019 22:28:38
если хочется объяснения и/или еще формул — можно заглянуть в калейдоскоп
Victor Kleptsyn
М
16:50
Математические байки
In reply to this message
Посмотрим сначала на классическое доказательство теоремы Штурма. Если мы говорим о том, что число корней P на отрезке [a,b] выражается через изменение на этом отрезке числа перемен знака — так очень естественно спросить себя, а как вообще число перемен знака N(x) меняется, когда меняется x?
Естественно, что меняться оно может только если меняет знак какой-то из многочленов P_j. Но — и это замечательно — если меняет знак (переходя через ноль) любой P_j, кроме P_1, то число перемен знака не меняется.
Действительно, пусть в точке x_0 обращается в ноль какой-то P_j, и j>1. Его соседи тогда в этой точке не обращаются в ноль: иначе там обратились бы в ноль и все полиномы вообще, а у P_1 и P_2 нет общих корней.
Но заметим, что его соседи противоположного знака: ведь
P_{j-1} + P_{j+1} = P_j * Q_{j-1},
раз правая часть обратилась в ноль, то и сумма соседей P_{j-1}+P_{j+1} в точке x_0 обращается в ноль.
А тогда неважно, какой у P_j рядом с x_0 знак — всё равно на P_{j-1},P_j,P_{j+1} приходится ровно одна перемена знака!
И мы, собственно, такое уже видели, когда смотрели на пример P(x)=x^2: рядом с x_0=0, где обращается в ноль производная P_2=2x, число перемен знака не менялось:
===
-0.1: -,-,+; 1 перемена;
0.1: -,+,+; 1 перемена;
===
Естественно, что меняться оно может только если меняет знак какой-то из многочленов P_j. Но — и это замечательно — если меняет знак (переходя через ноль) любой P_j, кроме P_1, то число перемен знака не меняется.
Действительно, пусть в точке x_0 обращается в ноль какой-то P_j, и j>1. Его соседи тогда в этой точке не обращаются в ноль: иначе там обратились бы в ноль и все полиномы вообще, а у P_1 и P_2 нет общих корней.
Но заметим, что его соседи противоположного знака: ведь
P_{j-1} + P_{j+1} = P_j * Q_{j-1},
раз правая часть обратилась в ноль, то и сумма соседей P_{j-1}+P_{j+1} в точке x_0 обращается в ноль.
А тогда неважно, какой у P_j рядом с x_0 знак — всё равно на P_{j-1},P_j,P_{j+1} приходится ровно одна перемена знака!
И мы, собственно, такое уже видели, когда смотрели на пример P(x)=x^2: рядом с x_0=0, где обращается в ноль производная P_2=2x, число перемен знака не менялось:
===
-0.1: -,-,+; 1 перемена;
0.1: -,+,+; 1 перемена;
===
Victor Kleptsyn
М
17:55
Математические байки
Так что переходы значений "внутренних" полиномов через ноль на число перемен знака не влияют. P_n=1 через ноль перейти вообще не может, это константа. Остаётся только P_1.
А значение многочлена P переходит через ноль — правее корня знак у P такой же, как у его производной P' в этом корне, а левее корня противоположный. Поэтому как раз при переходе через ноль P (и только там) число перемен знака уменьшается на единицу. Теорема Штурма доказана.
Осталось это склеить с тем взглядом, который у нас был раньше.
А значение многочлена P переходит через ноль — правее корня знак у P такой же, как у его производной P' в этом корне, а левее корня противоположный. Поэтому как раз при переходе через ноль P (и только там) число перемен знака уменьшается на единицу. Теорема Штурма доказана.
Осталось это склеить с тем взглядом, который у нас был раньше.
Victor Kleptsyn
М
20:42
Математические байки
Да, если P_1 и P_2 произвольные без общих корней, то большая часть рассуждения выше тоже работает. Только разница в числе перемен знака на отрезке [a,b] считает не просто корни P_1 — а корни P_1 со знаком: если в корне P_1' и P_2 одного знака, то мы его считаем с плюсом, а если разного, то с минусом. (Потому что именно так пересечение корня P_1 меняет число перемен знака — а пересечение корней всех остальных P_j, как и раньше, ничего не меняет.)
Victor Kleptsyn
20:50
In reply to this message
Собственно, это буквально соответствует вычислению части суммы для топологической степени deg_{top} P_1/P_2 по прообразу нуля (то есть по пересечению с вертикальной прямой на плоскости (P_1,P_2)), когда мы ограничиваемся прообразами из отрезка параметров [a,b].
Victor Kleptsyn
20:54
In reply to this message
Понять, что выкладки через цепную дробь приводят к тому же результату, не очень сложно. Действительно, когда мы делим с остатком, то знаки P_j и P_{j+1} отличаются на знак неполного частного Q_j (а P_{j+1} слишком мал, и ни на что не влияет). Соответственно, если многочлен Q_j в данной (плюс или минус) бесконечности отрицателен, то перемена знака между P_j и P_{j+1} там есть, а если положителен, то нет. Вот и получается, что когда мы считаем разницу между числом перемен знака в минус и в плюс бесконечности, то Q_j чётной степени вклада не дают (ибо они в бесконечностях одного знака), а Q_j нечётной степени дают вклад, равный знаку старшего коэффициента.
Так что ответы "через цепную дробь" и "через перемены знаков" для числа всех вещественных нулей (и для топологической степени рациональной функции R=P_1/P_2) совпадают. Уже хорошо.
Но хотелось бы как-то понять, как о переменах знака думать в топологических терминах — при том, что для отображения отрезка о степени уже говорить нельзя, у него концы есть.
Так что ответы "через цепную дробь" и "через перемены знаков" для числа всех вещественных нулей (и для топологической степени рациональной функции R=P_1/P_2) совпадают. Уже хорошо.
Но хотелось бы как-то понять, как о переменах знака думать в топологических терминах — при том, что для отображения отрезка о степени уже говорить нельзя, у него концы есть.
Victor Kleptsyn
17 March 2021
М
11:59
Математические байки
На самом деле, история довольно простая — и параллельная тому, что мы уже делали. А именно — разложение рациональной функции
R=P_1/P_2
в цепную дробь Хирцебруха ("с минусами") разбивается в череду операций:
*) повернуть картинку на 90 градусов (P_1,P_2) -> (P_2,-P_1)
*) добавить к второй координате первую, умноженную на Q_1
(P_2,-P_1) -> (P_2, Q_1*P_2-P_1) = (P_2,P_3)
*) повернуть картинку на 90 градусов (P_2,P_3) -> (P_3,-P_2)
*) добавить к второй координате первую, умноженную на Q_2
(P_3,-P_2) -> (P_3, Q_2*P_3-P_2) = (P_3,P_4)
*) и так далее.
R=P_1/P_2
в цепную дробь Хирцебруха ("с минусами") разбивается в череду операций:
*) повернуть картинку на 90 градусов (P_1,P_2) -> (P_2,-P_1)
*) добавить к второй координате первую, умноженную на Q_1
(P_2,-P_1) -> (P_2, Q_1*P_2-P_1) = (P_2,P_3)
*) повернуть картинку на 90 градусов (P_2,P_3) -> (P_3,-P_2)
*) добавить к второй координате первую, умноженную на Q_2
(P_3,-P_2) -> (P_3, Q_2*P_3-P_2) = (P_3,P_4)
*) и так далее.
Victor Kleptsyn
12:15
In reply to this message
После чего продолжили в том же духе. Так вот — на операциях "добавить" мы пересечения с осью ординат не меняем (потому что добавляем первую координату, на что-то там умноженную). И их тип (по или против часовой стрелки) тоже.
Victor Kleptsyn
12:19
In reply to this message
А вот на операциях "повернуть" — можем поменять. Потому что сначала мы считали (с учётом знака) пересечения с одной прямой, а потом с другой. Если бы мы работали с замкнутой кривой, то мы бы считали буквально степень отображения окружности, и ничего поменяться бы не могло, потому что при повороте прямой прообразы бы только сливались "плюс с минусом", и ничего бы не менялось. Но если мы работаем с отрезком [a,b] параметров — то у отрезка кривой есть концы. И вот тут-то мы с числом перемен знака и столкнёмся!
Victor Kleptsyn
12:22
Уже звучит очень естественно, что важно, пересекут ли в процессе поворота (кривой или системы координат — кому как удобнее) концы кривой ось ординат, пересечения с которой мы считаем. Но проще всего в этом убедиться, уронив всю ситуацию обратно на проективную прямую (= окружность, образуемую всеми прямыми через ноль).
Victor Kleptsyn
12:27
In reply to this message
Если по окружности-стадиону бежит атлет и возвращается в итоге в начальную точку — число кругов, которые он пробежал, можно посчитать, встав в любую точку стадиона и считая пересечения (если он пробежал куда надо, то с плюсом, а если обратно, то с минусом).
А если траектория атлета незамкнута — то арбитры, стоящие в разных точках круга, могут получить разные суммы. Но не сильно: если атлет начал и закончил бежать на одной и той же дуге, то их результаты совпадут — потому что он после этого может пройтись от конца своего пути к началу, не проходя мимо арбитров, и получить уже замкнутый путь.
А если траектория атлета незамкнута — то арбитры, стоящие в разных точках круга, могут получить разные суммы. Но не сильно: если атлет начал и закончил бежать на одной и той же дуге, то их результаты совпадут — потому что он после этого может пройтись от конца своего пути к началу, не проходя мимо арбитров, и получить уже замкнутый путь.
Victor Kleptsyn
М
12:54
Математические байки
А если атлет начинал и закончил путь на разных дугах — то если добавить к пути замыкание "в положительном направлении", после которого суммы у арбитров совпадут, то один из двух арбитров его увидит, а другой нет. И уже совсем легко увидеть, что общий ответ такой:
число пересечений (с учётом знака) для арбитра A1 минус
число пересечений (с учётом знака) для арбитра А2 =
F(начала пути)-F(конца пути),
где F это 1, если мы начали на дуге от A2 к A1 (обозначенной тут +-), и 0 иначе.
число пересечений (с учётом знака) для арбитра A1 минус
число пересечений (с учётом знака) для арбитра А2 =
F(начала пути)-F(конца пути),
где F это 1, если мы начали на дуге от A2 к A1 (обозначенной тут +-), и 0 иначе.
Victor Kleptsyn
12:59
Если просуммировать такое за все шаги, то получается:
Число пересечений с осью ординат для исходной кривой (которое и есть то, что мы ищем)
минус
число пересечений с осью ординат для последней кривой, к которой мы приходим (а это просто точка (1,0), которая стоит на месте и ось ординат не пересекает)
равно
сумме по всем шагам разностей F(начало пути) минус F(конца пути), где F смотрит, есть ли между P_j и P_{j+1} перемена знака.
Потому что арбитры в нашем случае это ось ординат (до поворота) и ось абсцисс (после), и вот дуга между ними это и есть "координаты разного знака".
Ну а сумма разностей это разность сумм, и каждая из сумм это и есть общее число перемен знака в последовательности!
Число пересечений с осью ординат для исходной кривой (которое и есть то, что мы ищем)
минус
число пересечений с осью ординат для последней кривой, к которой мы приходим (а это просто точка (1,0), которая стоит на месте и ось ординат не пересекает)
равно
сумме по всем шагам разностей F(начало пути) минус F(конца пути), где F смотрит, есть ли между P_j и P_{j+1} перемена знака.
Потому что арбитры в нашем случае это ось ординат (до поворота) и ось абсцисс (после), и вот дуга между ними это и есть "координаты разного знака".
Ну а сумма разностей это разность сумм, и каждая из сумм это и есть общее число перемен знака в последовательности!
Victor Kleptsyn
13:09
Ура, победа! Мы связали топологический взгляд с классической формулировкой теоремы Штурма через число перемен знака.
Victor Kleptsyn
13:14
Ещё — пара картинок из "Геометрии дискриминанта" В. А. Васильева:
Victor Kleptsyn
13:20
Топологическая степень это ответ на вопрос, почему в множестве пар многочленов (ровно) второй степени без общих корней нельзя пройти от пары "корни чередуются" к паре "корни не чередуются" (и кстати, нельзя поменять порядок чередования корней). Ибо при одном чередовании будет обход по часовой стрелке, при другом против, а при отсутствии чередования степень нулевая.
Victor Kleptsyn
13:24
In reply to this message
А вот — страница из текста Д. В. Аносова 2003 года; как раз очень близко к тому, что мы уже видели раньше, только у него цепная дробь обычная, поэтому в ответе возникает чередование знаков:
Victor Kleptsyn
13:26
Ну а часть рассказа выше (подход через степени) вошла в (онлайн)-курс топологии, который мы с коллегами ведём — собственно, уже заканчиваем — для первого курса Вышки. Кто же знал, когда всё это только задумывалось, что курс с частичным онлайном и красивыми картинками вынужденно превратится в полный онлайн...
From behind the stages:
From behind the stages:
Victor Kleptsyn
М
13:58
Математические байки
Через пару минут начнётся объявление премии Абеля:
https://www.youtube.com/watch?v=0_NK_OkpmUY
https://www.youtube.com/watch?v=0_NK_OkpmUY
Victor Kleptsyn
М
14:05
Математические байки
Н
Непрерывное математическое образование 17.03.2021 14:05:00
Abel Prize 2021:
László Lovász & Avi Wigderson
“for their foundational contributions to theoretical computer science and discrete mathematics, and their leading role in shaping them into central fields of modern mathematics”
László Lovász & Avi Wigderson
“for their foundational contributions to theoretical computer science and discrete mathematics, and their leading role in shaping them into central fields of modern mathematics”
Victor Kleptsyn
М
19 March 2021
М
15:29
Математические байки
In reply to this message
Один из результатов, который упоминали на церемонии вручения премии Абеля — это Zero Knowledge Proof, доказательство с нулевым разглашением. И это действительно очень красивая идея (восходящая к работе Goldreich-Micali-Rackoff, "The Knowledge Complexity of Interactive Proof-Systems").
Как мне это когда-то рассказывали — вот представьте себе, что математик X доказал гипотезу Римана. Естественно было бы написать статью или рассказать результат на семинаре — но X опасается, что его результат украдут. Может ли X убедить коллег, что у него действительно есть доказательство — не рассказав его? И оказывается, что да, есть способ это сделать — о доказательстве вообще ничего не рассказав, кроме его длины. (Можно считать, что X потрясает пачкой бумаги со словами, "этого хватит, чтобы доказательство записать".)
Более того, — это возможно для вообще любой NP-задачи. И вот тут алгоритм придумали Oded Goldreich, Silvio Micali и Avi Wigderson: см. "How to Prove All NP Statements in Zero-Knowledge and a Methodology of Cryptographic Protocol Design" (1986; https://link.springer.com/content/pdf/10.1007%2F3-540-47721-7_11.pdf )
В двух словах (я уточню ближе к концу этого рассказа) — нас интересуют ситуации, когда уже предъявленный ответ можно быстро проверить, но вот сам поиск этого ответа, возможно, безумно сложен. Например, если Вася хочет доказать, что он знает гамильтонов (посещающего каждую вершину ровно один раз) путь в графе. Как раз — проверить, что путь по 1000 вершин графа действительно проходит через каждую вершину, ровно один раз, и каждый раз переходит по ребру — легко. А вот найти такой путь (если он есть) для заданного графа — слоожно...
Тот пример, из которого всё выводится в работе Goldreich, Micali, Wigderson — это задача трёхцветной раскраски: раскрасить вершины графа в 3 цвета так, чтобы соседние вершины были бы раскрашены в разные цвета.
(Кстати: если граф планарный, то в четыре цвета его вершины правильным образом раскрасить всегда можно — и это и утверждает теорема о четырёх красках.)
Понятно, что это задача как раз такого класса: найти раскраску может быть очень сложно — но вот когда раскраска уже предъявлена, проверить, что это действительно правильная раскраска, занимает вполне разумное время.
Так вот — допустим, что X знает правильную трёхцветную раскраску данного графа. Как ему убедить в этом Y, не раскрывая никакой информации?
Как мне это когда-то рассказывали — вот представьте себе, что математик X доказал гипотезу Римана. Естественно было бы написать статью или рассказать результат на семинаре — но X опасается, что его результат украдут. Может ли X убедить коллег, что у него действительно есть доказательство — не рассказав его? И оказывается, что да, есть способ это сделать — о доказательстве вообще ничего не рассказав, кроме его длины. (Можно считать, что X потрясает пачкой бумаги со словами, "этого хватит, чтобы доказательство записать".)
Более того, — это возможно для вообще любой NP-задачи. И вот тут алгоритм придумали Oded Goldreich, Silvio Micali и Avi Wigderson: см. "How to Prove All NP Statements in Zero-Knowledge and a Methodology of Cryptographic Protocol Design" (1986; https://link.springer.com/content/pdf/10.1007%2F3-540-47721-7_11.pdf )
В двух словах (я уточню ближе к концу этого рассказа) — нас интересуют ситуации, когда уже предъявленный ответ можно быстро проверить, но вот сам поиск этого ответа, возможно, безумно сложен. Например, если Вася хочет доказать, что он знает гамильтонов (посещающего каждую вершину ровно один раз) путь в графе. Как раз — проверить, что путь по 1000 вершин графа действительно проходит через каждую вершину, ровно один раз, и каждый раз переходит по ребру — легко. А вот найти такой путь (если он есть) для заданного графа — слоожно...
Тот пример, из которого всё выводится в работе Goldreich, Micali, Wigderson — это задача трёхцветной раскраски: раскрасить вершины графа в 3 цвета так, чтобы соседние вершины были бы раскрашены в разные цвета.
(Кстати: если граф планарный, то в четыре цвета его вершины правильным образом раскрасить всегда можно — и это и утверждает теорема о четырёх красках.)
Понятно, что это задача как раз такого класса: найти раскраску может быть очень сложно — но вот когда раскраска уже предъявлена, проверить, что это действительно правильная раскраска, занимает вполне разумное время.
Так вот — допустим, что X знает правильную трёхцветную раскраску данного графа. Как ему убедить в этом Y, не раскрывая никакой информации?
Victor Kleptsyn
15:29
Сделаем вот что: пусть X выберет случайным образом одну из 6 перестановок цветов (ведь если перекрасить все красные вершины в зелёный, а все зелёные в красный — правильная раскраска останется правильной). И положит у каждой вершины запечатанный конверт с цветом получившейся правильной раскраски.
Теперь проверяющий Y выберет две соседние вершины. И вскроет соответствующие им конверты (все остальные конверты немедленно сжигаются).
Дальше может быть одно из двух:
1) Если Y обнаружил совпадающие цвета, то он говорит X "ах ты нехороший человек, обмануть хотел? Не прокатило!". На этом протокол прекращается, а X объявляется жуликом.
2) Если цвета разные, то процедура повторяется. X выбирает новую случайную перестановку, раскладывает конверты, Y выбирает две соседние вершины, вскрывает конверты в них, и так далее.
При этом — если X играет честно и выбирает каждый раз равномерно случайную перестановку, то никакой информации о раскраске (кроме того, что она, похоже, правильная) Y не получает: любая пара соседних вершин может быть равновероятно окрашена любым из 6 способов.
Наоборот, если Y выбирает проверяемое ребро случайным образом, то шанс поймать X, если он жульничает — по меньшей мере 1/N, где N — число рёбер в графе. За 100N раундов шанс, что на самом деле не знающий раскраски обманщик не будет пойман, становится меньше
(1- 1/N)^{100N} ~ e^{-100} < 10^{-40}.
(Ну и, естественно, такая вероятность может быть сделана сколь угодно малой, если 10^{-40} нам почему-то недостаточно.)
Теперь проверяющий Y выберет две соседние вершины. И вскроет соответствующие им конверты (все остальные конверты немедленно сжигаются).
Дальше может быть одно из двух:
1) Если Y обнаружил совпадающие цвета, то он говорит X "ах ты нехороший человек, обмануть хотел? Не прокатило!". На этом протокол прекращается, а X объявляется жуликом.
2) Если цвета разные, то процедура повторяется. X выбирает новую случайную перестановку, раскладывает конверты, Y выбирает две соседние вершины, вскрывает конверты в них, и так далее.
При этом — если X играет честно и выбирает каждый раз равномерно случайную перестановку, то никакой информации о раскраске (кроме того, что она, похоже, правильная) Y не получает: любая пара соседних вершин может быть равновероятно окрашена любым из 6 способов.
Наоборот, если Y выбирает проверяемое ребро случайным образом, то шанс поймать X, если он жульничает — по меньшей мере 1/N, где N — число рёбер в графе. За 100N раундов шанс, что на самом деле не знающий раскраски обманщик не будет пойман, становится меньше
(1- 1/N)^{100N} ~ e^{-100} < 10^{-40}.
(Ну и, естественно, такая вероятность может быть сделана сколь угодно малой, если 10^{-40} нам почему-то недостаточно.)
Victor Kleptsyn
15:39
In reply to this message
==
Вообще-то говоря, я тут смешал в одно описание ("что будет происходить") две вещи: протокол и стратегию игроков . Если их разделять — а это правильно сделать — то протокол состоит в том, что на каждой итерации X кладёт конверты, а Y выбирает из них два, отвечающих соседним вершинам, после чего они вскрываются. И если обнаруживают два одинаковых цвета, то X проиграл, а если за данное большое число раундов X не пойман, то считается, что он Y убедил.
А дальше — честный X с помощью стратегии случайной перестановки цветов на каждом шаге гарантирует, что информация не утечёт при любых действиях Y (какое бы ребро Y ни выбрал, он получает просто равновероятную пару цветов).
Наоборот, честный Y с помощью стратегии случайного выбора ребра на каждом шаге гарантирует, что вероятность для жулика-X проскочить не больше, чем 10^{-40} (и вообще экспоненциально мала по количеству итераций протокола).
А вообще протоколы, стратегии и атаки на протоколы — это большая тонкая наука (и туда мы сейчас точно не пойдём 🙂 ).
==
Вообще-то говоря, я тут смешал в одно описание ("что будет происходить") две вещи: протокол и стратегию игроков . Если их разделять — а это правильно сделать — то протокол состоит в том, что на каждой итерации X кладёт конверты, а Y выбирает из них два, отвечающих соседним вершинам, после чего они вскрываются. И если обнаруживают два одинаковых цвета, то X проиграл, а если за данное большое число раундов X не пойман, то считается, что он Y убедил.
А дальше — честный X с помощью стратегии случайной перестановки цветов на каждом шаге гарантирует, что информация не утечёт при любых действиях Y (какое бы ребро Y ни выбрал, он получает просто равновероятную пару цветов).
Наоборот, честный Y с помощью стратегии случайного выбора ребра на каждом шаге гарантирует, что вероятность для жулика-X проскочить не больше, чем 10^{-40} (и вообще экспоненциально мала по количеству итераций протокола).
А вообще протоколы, стратегии и атаки на протоколы — это большая тонкая наука (и туда мы сейчас точно не пойдём 🙂 ).
==
Victor Kleptsyn
М
16:14
Математические байки
Вот тут есть демонстрация этого алгоритма со стороны проверяющего:
http://web.mit.edu/~ezyang/Public/graph/svg.html
Там предлагают выбрать граф — и в одном из случаев к нам пришёл человек с честной раскраской, а в другом нас пытаются обмануть. Confidence внизу отвечает за оценку на "1 минус вероятность того, что обманщику столько раундов подряд бы везло".
http://web.mit.edu/~ezyang/Public/graph/svg.html
Там предлагают выбрать граф — и в одном из случаев к нам пришёл человек с честной раскраской, а в другом нас пытаются обмануть. Confidence внизу отвечает за оценку на "1 минус вероятность того, что обманщику столько раундов подряд бы везло".
Victor Kleptsyn
М
16:47
Математические байки
==
Да, ещё одно — как можно реализовать конверты: хэшем. Если есть (объявлена публично) односторонняя функция F (которую трудно обратить, но которая тем не менее взаимно-однозначна), то пусть X на каждом шаге для каждой вершины j вычисляет
f_j=F(c_j R_j),
где с_j — пара бит, кодирущих цвет в этой вершине, а R_j — ещё куча-куча "мусорных бит", и объявляет результат вычисления f_j публично. (Мусор нужен, чтобы Y не мог просто перебрать три варианта цвета и вычислить от них F; если я правильно понимаю, такой мусор в криптографии называется "солью").
И протокол дополняется тем, как происходит "вскрытие конвертов": Y говорит, какие именно конверты вскрывает, X для них объявляет c_j и R_j, после чего Y проверяет, что F от заявленных c_j R_j это действительно ранее объявленные f_j.
А стратегия X — тем, что мусорные биты нужно выбирать совершенно случайными, чтобы объявление f_j и впрямь не приводило ни к какой (значимой) утечке информации.
==
Да, ещё одно — как можно реализовать конверты: хэшем. Если есть (объявлена публично) односторонняя функция F (которую трудно обратить, но которая тем не менее взаимно-однозначна), то пусть X на каждом шаге для каждой вершины j вычисляет
f_j=F(c_j R_j),
где с_j — пара бит, кодирущих цвет в этой вершине, а R_j — ещё куча-куча "мусорных бит", и объявляет результат вычисления f_j публично. (Мусор нужен, чтобы Y не мог просто перебрать три варианта цвета и вычислить от них F; если я правильно понимаю, такой мусор в криптографии называется "солью").
И протокол дополняется тем, как происходит "вскрытие конвертов": Y говорит, какие именно конверты вскрывает, X для них объявляет c_j и R_j, после чего Y проверяет, что F от заявленных c_j R_j это действительно ранее объявленные f_j.
А стратегия X — тем, что мусорные биты нужно выбирать совершенно случайными, чтобы объявление f_j и впрямь не приводило ни к какой (значимой) утечке информации.
==
Victor Kleptsyn
М
20:51
Математические байки
In reply to this message
Да, я исходно написал 1000N и оценку на вероятность в 10^{-400}, после чего коллеги ехидно сказали, что столь малую вероятность уже писать бессмысленно — её сильно мажорирует шанс на ошибочную операцию в процессоре (и много что ещё). Так что я остановился на добивании вероятности до разумно-очень-малой. 🙂
Victor Kleptsyn
22 March 2021
М
20:41
Математические байки
In reply to this message
И я обещал рассказать про то, что такое NP-задачи.
Определение NP-задачи такое: задача Q относится к классу NP, если
1) Она требует ответа вида Q(x)="да/нет" в зависимости от параметра x
и
2) Ответ "да" может быть доказан некоторой "справкой", проверяемой за полиномиальное время. Формально — существует такой алгоритм Check(x,S), "проверяющий" за полиномиальное по длине входа x время полиномиальный по длине входа x сертификат S:
- для любого x, для которого Q(x)="да", существует S, такой, что Check(x,S)="да";
- ни для одного x, для которого Q(x)="нет", не существует такого S, чтобы Check(x,S)="да"
(плюс ограничения на длину S и на время работы Check).
Стоит отметить, что постановка тут несимметрична по "да/нет": если вопрос Q="x верблюд?" принадлежит классу NP, ибо взятая в зоопарке справка S проверяется процедурой
Check(x,S)="проверить бланк справки, печать зоопарка и совпадение указанного там животного с x"
(при том, что предъявление S="мятая салфетка" не означает, что x не верблюд — а только то, что данная S этого не доказывает),
то где брать справку, что ты не верблюд, совершенно непонятно.
Менее абстрактный пример — вопрос о том, является ли данное натуральное число N составным, принадлежит классу NP. "Справкой" будет его разложение на два сомножителя, S=(a,b); процедура проверки —
Check(N,S)=
- проверить, что S=(a,b), где a,b натуральные и больше 1 (а то норовят всякие подсунуть строку вместо числа на вход).
- проверить, что N=ab.
(Последнее даже при выполнении умножения "в столбик" требует ~n^2 операций, где n — число цифр в записи N)
А вот принадлежность вопроса "является ли N простым" классу NP совершенно неочевидна. Потому что проверка "в лоб" подразумевала бы перебор делителей от 1 до корня из N — и это даже для N порядка 10^100 ну совершенно нереалистично. А как бы могла быть устроена короткая и быстро проверяемая "справка о простоте" — на вид непонятно.
(На самом деле, этот вопрос даже классу P принадлежит — но без дополнительных предположений это результат начала 2000-х: см. Agrawal, Kayal, Saxena, PRIMES in P, Annals of Mathematics, 2004 + https://en.wikipedia.org/wiki/AKS_primality_test )
Определение NP-задачи такое: задача Q относится к классу NP, если
1) Она требует ответа вида Q(x)="да/нет" в зависимости от параметра x
и
2) Ответ "да" может быть доказан некоторой "справкой", проверяемой за полиномиальное время. Формально — существует такой алгоритм Check(x,S), "проверяющий" за полиномиальное по длине входа x время полиномиальный по длине входа x сертификат S:
- для любого x, для которого Q(x)="да", существует S, такой, что Check(x,S)="да";
- ни для одного x, для которого Q(x)="нет", не существует такого S, чтобы Check(x,S)="да"
(плюс ограничения на длину S и на время работы Check).
Стоит отметить, что постановка тут несимметрична по "да/нет": если вопрос Q="x верблюд?" принадлежит классу NP, ибо взятая в зоопарке справка S проверяется процедурой
Check(x,S)="проверить бланк справки, печать зоопарка и совпадение указанного там животного с x"
(при том, что предъявление S="мятая салфетка" не означает, что x не верблюд — а только то, что данная S этого не доказывает),
то где брать справку, что ты не верблюд, совершенно непонятно.
Менее абстрактный пример — вопрос о том, является ли данное натуральное число N составным, принадлежит классу NP. "Справкой" будет его разложение на два сомножителя, S=(a,b); процедура проверки —
Check(N,S)=
- проверить, что S=(a,b), где a,b натуральные и больше 1 (а то норовят всякие подсунуть строку вместо числа на вход).
- проверить, что N=ab.
(Последнее даже при выполнении умножения "в столбик" требует ~n^2 операций, где n — число цифр в записи N)
А вот принадлежность вопроса "является ли N простым" классу NP совершенно неочевидна. Потому что проверка "в лоб" подразумевала бы перебор делителей от 1 до корня из N — и это даже для N порядка 10^100 ну совершенно нереалистично. А как бы могла быть устроена короткая и быстро проверяемая "справка о простоте" — на вид непонятно.
(На самом деле, этот вопрос даже классу P принадлежит — но без дополнительных предположений это результат начала 2000-х: см. Agrawal, Kayal, Saxena, PRIMES in P, Annals of Mathematics, 2004 + https://en.wikipedia.org/wiki/AKS_primality_test )
Victor Kleptsyn
26 March 2021
М
12:44
Математические байки
Давайте я закончу рассказ про NP и вокруг того. Мы пока сказали, что такое класс NP.
В начале 1970-х поняли две вещи: во-первых, в классе NP есть "самая сложная задача" — к которой любая другая NP-задача за полиномиальное время сводится. И во-вторых, что таких задач (сводящихся друг к другу) много.
Предъявить одну такую задачу совсем просто: собственно говоря, она практически уже выписана выше. А именно: пусть нам задан алгоритм C и полиномы P_1, P_2.
Q(x)="найдётся ли второй вход S, длины |S|<P_1(|x|), на котором за время не больше P_2(|x|) алгоритм C закончит работу и выдаст "да"? "
Такая задача явно принадлежит классу NP: если S уже задан, то нужно просто "в режиме интерпретатора" сделать P_2(|x|) шагов заданного алгоритма C и проверить, куда мы придём.
И любая NP-задача к ней сводится — для неё C это тот самый её алгоритм Check из определения!
Так что — вот наш первый пример NP-полной задачи.
Из него сразу можно получить ещё один — выполнимость булевской формулы. Допустим, что у нас написана булевская формула из переменных, их отрицаний (¬), конъюнкций (И, ⋀) и дизъюнкций (ИЛИ, ⋁). Можно ли подставить вместо переменных булевские единицы и нули (True и False) так, чтобы вся формула давала единицу?
Очевидно, что эта задача принадлежит классу NP: сертификат это как раз то, что нужно подставить. А почему она NP-полна?
Достаточно к ней свести уже увиденную нами NP-полную задачу, "найдётся ли S длины |S|<P_1(|x|) такой, что C(x,S)="да" за время P_2(|x|)".
Посмотрим на "протокол работы алгоритма C": закодируем нулями и единицами состояние каждой ячейки памяти в каждый момент времени. Тогда то, что набор нулей и единиц корректно кодирует протокол — это большая булевская формула, что в каждый момент времени и в каждой ячейке переход от этого момента времени к следующему выполнен правильно. Начальные условия (где нужно написать, что часть начальных данных это вход x, поставить пишуще-читающую головку машины Тьюринга на исходную позицию и в начальном состоянии, и так далее) и то, что алгоритм заканчивает работу и печатает "да" — это тоже просто требование на часть переменных (подстановка нулей и единиц вместо некоторых из них). И вот и всё сведение!
Более того — такая формула это всегда большая-большая конъюнкция довольно простых выражений "для любого t для любого места m [переход в точке пространства-времени (m,t) выполнен правильно]". Так что даже вопрос про такие формулы уже NP-полон.
Если мысленно собрать все переходы из логических элементов — а именно, достаточно иметь лишь И-НЕ — то у нас будет формула вида "переменная, приписанная к выходу каждого логического элемента, принимает то значение, которое задают его входы".
А это несложно задать конъюнкцией четырёх дизъюнкций: утверждение
"c=f(a,b)"
равносильно тому, что для каждой пары возможных значений a_0, b_0 мы пишем
"(a не равно a_0) ИЛИ (b не равно b_0) ИЛИ (с равно f(a_0,b_0))",
где вместо "переменная равна константе" мы ставим саму переменную, если константа это 1 и её отрицание, если константа это 0. Собственно, И-НЕ таким образом задаётся как "c=И-НЕ (a,b)" <=>
(¬a ИЛИ ¬b ИЛИ ¬c) И
(¬a ИЛИ b ИЛИ c) И
(a ИЛИ ¬b ИЛИ c) И
(a ИЛИ b ИЛИ c);
строчки тут соответствуют наборам входов и значениям 11->0, 10->1, 01->1, 00->1.
Так что NP-полна задача выполнимости булевской формулы, которая есть большая-большая конъюнкция скобок, в каждой из которых дизъюнкция всего-то трёх переменных или их отрицаний. И эта задача называется 3-SAT.
В начале 1970-х поняли две вещи: во-первых, в классе NP есть "самая сложная задача" — к которой любая другая NP-задача за полиномиальное время сводится. И во-вторых, что таких задач (сводящихся друг к другу) много.
Предъявить одну такую задачу совсем просто: собственно говоря, она практически уже выписана выше. А именно: пусть нам задан алгоритм C и полиномы P_1, P_2.
Q(x)="найдётся ли второй вход S, длины |S|<P_1(|x|), на котором за время не больше P_2(|x|) алгоритм C закончит работу и выдаст "да"? "
Такая задача явно принадлежит классу NP: если S уже задан, то нужно просто "в режиме интерпретатора" сделать P_2(|x|) шагов заданного алгоритма C и проверить, куда мы придём.
И любая NP-задача к ней сводится — для неё C это тот самый её алгоритм Check из определения!
Так что — вот наш первый пример NP-полной задачи.
Из него сразу можно получить ещё один — выполнимость булевской формулы. Допустим, что у нас написана булевская формула из переменных, их отрицаний (¬), конъюнкций (И, ⋀) и дизъюнкций (ИЛИ, ⋁). Можно ли подставить вместо переменных булевские единицы и нули (True и False) так, чтобы вся формула давала единицу?
Очевидно, что эта задача принадлежит классу NP: сертификат это как раз то, что нужно подставить. А почему она NP-полна?
Достаточно к ней свести уже увиденную нами NP-полную задачу, "найдётся ли S длины |S|<P_1(|x|) такой, что C(x,S)="да" за время P_2(|x|)".
Посмотрим на "протокол работы алгоритма C": закодируем нулями и единицами состояние каждой ячейки памяти в каждый момент времени. Тогда то, что набор нулей и единиц корректно кодирует протокол — это большая булевская формула, что в каждый момент времени и в каждой ячейке переход от этого момента времени к следующему выполнен правильно. Начальные условия (где нужно написать, что часть начальных данных это вход x, поставить пишуще-читающую головку машины Тьюринга на исходную позицию и в начальном состоянии, и так далее) и то, что алгоритм заканчивает работу и печатает "да" — это тоже просто требование на часть переменных (подстановка нулей и единиц вместо некоторых из них). И вот и всё сведение!
Более того — такая формула это всегда большая-большая конъюнкция довольно простых выражений "для любого t для любого места m [переход в точке пространства-времени (m,t) выполнен правильно]". Так что даже вопрос про такие формулы уже NP-полон.
Если мысленно собрать все переходы из логических элементов — а именно, достаточно иметь лишь И-НЕ — то у нас будет формула вида "переменная, приписанная к выходу каждого логического элемента, принимает то значение, которое задают его входы".
А это несложно задать конъюнкцией четырёх дизъюнкций: утверждение
"c=f(a,b)"
равносильно тому, что для каждой пары возможных значений a_0, b_0 мы пишем
"(a не равно a_0) ИЛИ (b не равно b_0) ИЛИ (с равно f(a_0,b_0))",
где вместо "переменная равна константе" мы ставим саму переменную, если константа это 1 и её отрицание, если константа это 0. Собственно, И-НЕ таким образом задаётся как "c=И-НЕ (a,b)" <=>
(¬a ИЛИ ¬b ИЛИ ¬c) И
(¬a ИЛИ b ИЛИ c) И
(a ИЛИ ¬b ИЛИ c) И
(a ИЛИ b ИЛИ c);
строчки тут соответствуют наборам входов и значениям 11->0, 10->1, 01->1, 00->1.
Так что NP-полна задача выполнимости булевской формулы, которая есть большая-большая конъюнкция скобок, в каждой из которых дизъюнкция всего-то трёх переменных или их отрицаний. И эта задача называется 3-SAT.
Victor Kleptsyn
М
14:05
Математические байки
In reply to this message
Давайте я чуть-чуть пообсуждаю параллели.
Мы раньше видели многочлен нескольких переменных, все положительные значения которого в неотрицательных целых точках — простые.
Мы раньше видели многочлен нескольких переменных, все положительные значения которого в неотрицательных целых точках — простые.
Victor Kleptsyn
14:06
In reply to this message
Разбираясь в том, как он работает — мы увидели, что все переменные, кроме одной, там как раз служат для кандидата в значение "справкой о простоте" (а если она не проходит проверку, то на этом наборе переменных значение автоматически становится неположительным). Правда, "справка" эта была вовсе не полиномиального размера!
Victor Kleptsyn
14:08
In reply to this message
И аккуратно разобрали более простые версии — сначала, как можно устроить справку, проверяемую с помощью факториала, а потом научились строить проверяющий для числа некоторую "справку о простоте" экспоненциально-полиномиальный многочлен.
Victor Kleptsyn
М
16:20
Математические байки
In reply to this message
Более того — решение десятой проблемы Гильберта как "любое перечислимое множество диофантово" устроено очень похоже на сведение к 3-SAT: чтобы нас убедить, что алгоритм -- машина Тьюринга, или, лучше, машина со счётчиками -- на данном входе хоть когда-нибудь останавливается, он приходит со справкой-сертификатом-протоколом своего выполнения, где (помимо всего прочего) записаны (в системе счисления с огромным основанием, "чтобы влезло") все состояния во все моменты времени. А многочлен проверяет, что все переходы действительно сделаны правильно (и для этого нужны ещё дополнительные переменные — они работают "справкой", удостоверяющей, что протокол-справка заполнен правильно).
Victor Kleptsyn
М
19:50
Математические байки
===
Вернёмся теперь к тому, с чего мы начинали: к задаче о существовании у данного графа правильной трёхцветной раскраски — 3-COL. И поймём, что она тоже NP-полна.
Опять же, понятно, что это NP-задача — остаётся к ней любую из NP-полных задач свести. И конечно, сводить нужно 3-SAT — рисуя такой граф, чтобы его правильная раскраска соответствовала набору значений переменных, на котором булевская формула будет выполнена.
Начнём с того, что нарисуем три попарно соединённые вершины: они гарантированно должны быть раскрашены в разные цвета. Поскольку цвета всё равно можно переставлять — будем считать, что тот цвет, который у левой вершины, это "0", у правой "1", а у оставшейся цвет назовём "база" (ни 0, ни 1).
Вернёмся теперь к тому, с чего мы начинали: к задаче о существовании у данного графа правильной трёхцветной раскраски — 3-COL. И поймём, что она тоже NP-полна.
Опять же, понятно, что это NP-задача — остаётся к ней любую из NP-полных задач свести. И конечно, сводить нужно 3-SAT — рисуя такой граф, чтобы его правильная раскраска соответствовала набору значений переменных, на котором булевская формула будет выполнена.
Начнём с того, что нарисуем три попарно соединённые вершины: они гарантированно должны быть раскрашены в разные цвета. Поскольку цвета всё равно можно переставлять — будем считать, что тот цвет, который у левой вершины, это "0", у правой "1", а у оставшейся цвет назовём "база" (ни 0, ни 1).
Victor Kleptsyn
19:52
Осталось сделать что-то, раскрашивание чего будет равносильно одной "скобке" X⋁Y⋁Z (где X,Y,Z — переменные или их отрицания). Вот если бы мы нарисовали ещё один треугольник и соединили его вершины с вершинами переменных/отрицаний X, Y и Z — то значения X=Y=Z=0 мы этим бы запретили (потому что из трёх вершин треугольника хоть одна нулём да будет раскрашена). Но вот беда — мы так и X=Y=Z=1 запретим, а этого бы не хотелось!
Victor Kleptsyn
19:52
Поэтому давайте сделаем так. Будем "подключать" переменные X, Y, Z к этому треугольнику не напрямую, а через дополнительные (специально для этой дизъюнкции выделенные) промежуточные вершины, соединённые ещё и с 1. Тогда если было X=Y=Z=0, то на промежуточных вершинах мы можем поставить только "базу" (потому что они соединены и с 0, и с 1), и продолжить раскраску на треугольник мы не сможем. Наоборот, если какая-то из переменных равна 1, то промежуточную вершину можно раскрасить как "0", и как "базу". И отсюда уже легко увидеть, что мы всегда можем раскрасить промежуточные вершины не все в один цвет — и дальше продлить эту раскраску на треугольник.
Victor Kleptsyn
19:53
Подключая по одному такому "удлинённому треугольнику" на каждую скобку, мы получаем граф, который можно правильно раскрасить в 3 цвета тогда и только тогда, когда есть значения переменных, обращающие булевскую формулу в истину. И вот 3-SAT сведена к 3-COL. Ура!
Victor Kleptsyn
М
20:28
Математические байки
In reply to this message
Так что, чтобы если X хочет нас убедить, что он умеет доказывать гипотезу Римана, не раскрывая доказательство — нужно попросить его записать его формально, в виде алгоритмически-проверяемой последовательности вывода (где каждая следующая строчка получается из предыдущих применением одного из правил вывода). Спрашиваем, какую длину его доказательство занимает (та самая пачка бумаги, которой он потрясает); резервируем под его доказательство ProofText ячейки алгоритма формальной проверки
CheckProof(RiemannHypothesis,ProofText).
Смотрим, сколько времени алгоритм будет работать, превращаем потенциальный протокол работы+"окончание работы с выводом "верно, доказано"" в булевскую формулу для 3-SAT. Переделываем её в граф для 3-COL. Ура — можно применить процедуру проверки!
CheckProof(RiemannHypothesis,ProofText).
Смотрим, сколько времени алгоритм будет работать, превращаем потенциальный протокол работы+"окончание работы с выводом "верно, доказано"" в булевскую формулу для 3-SAT. Переделываем её в граф для 3-COL. Ура — можно применить процедуру проверки!
Victor Kleptsyn
М
20:48
Математические байки
И в заключение — очень хороший (и совсем о другом) текст А. А. Разборова:
https://trv-science.ru/2021/03/pervoproxodcy-teoreticheskoj-informatiki/
https://trv-science.ru/2021/03/pervoproxodcy-teoreticheskoj-informatiki/
Victor Kleptsyn
28 March 2021
М
21:26
Математические байки
Н
Непрерывное математическое образование 28.03.2021 21:13:46
Берем число A, возводим в степень n, округляем до целого вверх. Бывает ли такое A, что все время (при всех натуральных n) получается число, отличающееся от полного квадрата ровно на 2?
// задача Д.Крекова на ММО сегодня, https://olympiads.mccme.ru/mmo/2021/
// задача Д.Крекова на ММО сегодня, https://olympiads.mccme.ru/mmo/2021/
Victor Kleptsyn
М
21:26
Математические байки
(теперь — с правильной ссылкой)
Victor Kleptsyn
21:27
Да, а задача правда красивая!
Victor Kleptsyn
31 March 2021
М
17:38
Математические байки
Н
Непрерывное математическое образование 31.03.2021 16:33:42
https://mccme.ru/dubna/2021/
Летняя школа «Современная математика» имени Виталия Арнольда планируется в этом году с 19 по 30 июля в Дубне (в очном формате). Начинается прием заявок от школьников 10 и 11 классов и студентов I и II курсов.
Летняя школа «Современная математика» имени Виталия Арнольда планируется в этом году с 19 по 30 июля в Дубне (в очном формате). Начинается прием заявок от школьников 10 и 11 классов и студентов I и II курсов.
Victor Kleptsyn
1 April 2021
М
18:24
Математические байки
Прекрасное прошлогоднее: самый обычный топологический препринт на arXiv-е: https://arxiv.org/pdf/2003.13758.pdf (картинка — одна страница оттуда).
Rami Luisto, "A non-Euclidean story or: how to persist when your geometry doesn’t."
Статья должна читаться как роман!
Rami Luisto, "A non-Euclidean story or: how to persist when your geometry doesn’t."
Статья должна читаться как роман!
Victor Kleptsyn
М
19:35
Математические байки
Н
Непрерывное математическое образование 01.04.2021 19:01:55
https://youtu.be/O85OWBJ2ayo
3blue1brown всегда интересно смотреть,
а отдельно приятно, что «The book shown at the start is Vladimir Arnold's (excellent) textbook on ordinary differential equations» ( https://biblio.mccme.ru/node/6102/ )
3blue1brown всегда интересно смотреть,
а отдельно приятно, что «The book shown at the start is Vladimir Arnold's (excellent) textbook on ordinary differential equations» ( https://biblio.mccme.ru/node/6102/ )
Victor Kleptsyn
6 April 2021
М
13:11
Математические байки
t
tropical saint petersburg 06.04.2021 13:10:06
Экслюзив: Письмо Рохлина Гудкову о том, что он доказал его гипотезу."Без сомнения, это доказательство лучше выражает топологическую суть дела, чем первое. Оно не было найдено сразу просто потому, что общая топологическая теорема, на которой оно основано [т.е. сравнение κ(F)−σ(X) ≡ 2τ(F)mod 8] не была известна. Вероятно, я скоро напишу это доказательство подробно. Конечно, я пришлю его Вам. Не знаю, сможете ли Вы ещё учесть его в Вашем обзоре.
Напишите, пожалуйста, нет ли аналогичных гипотез, относящихся к другим ситуациям, например, к кри- вым нечётной степени, к поверхностям или к неплоским кривым." 21.03.1972.
Подробнее.
Victor Kleptsyn
10 April 2021
М
17:51
Математические байки
М
Математические этюды 10.04.2021 17:49:43
Эйлеровой характеристикой многогранника называется число χ=В−Р+Г, где В, Р и Г — количества его вершин, ребер и граней соответственно. Оказывается, эйлерова характеристика зависит лишь от числа «дырок» в многограннике, например для многогранников без дырок (или как говорят математики, односвязных многогранников) эйлерова характеристика равна 2. То есть для куба, тетраэдра, октаэдра и любого другого многогранника без дыр χ=2. А для многогранника с g дырами χ=2−2g. Используя эйлерову характеристику, можно доказать несуществование некоторых многогранников. Например, не существует многогранника без дыр или с одной дыркой, у которого все грани — шестиугольники, попробуйте это проверить самостоятельно. Но если убрать условие на число дырок, то такие многогранники уже можно найти. Гораздо сложнее найти такой многогранник, все грани которого — выпуклые шестиугольники. На сегодняшней картинке изображён один такой многогранник. Попробуйте вычислить число его дырок :)
#рисункиМихаилаПанова
#которисунки
#MetaPost
#рисункиМихаилаПанова
#которисунки
#MetaPost
Victor Kleptsyn
М
21:44
Математические байки
Н
Непрерывное математическое образование 10.04.2021 15:23:14
https://knife.media/viktor-vasilyev/
к 65-летию Виктора Анатольевича Васильева — его недавнее интервью
к 65-летию Виктора Анатольевича Васильева — его недавнее интервью
Victor Kleptsyn
М
21:58
Математические байки
А ещё — давайте я вспомню "Геометрию дискриминанта" и "Ветвящиеся объёмы и группы отражений" (этот курс Васильев читал в ЛШСМ два года — в 2013 и в 2014 годах — после первого раза решив одну из открытых проблем в этой области, так что на следующий год он уже рассказывал её решение. А недавно из этих курсов получилась, как мне кажется, замечательная книга для матшкольников и студентов — куда и это решение тоже вошло!).
Victor Kleptsyn
11 April 2021
М
14:26
Математические байки
In reply to this message
Давайте я выложу несколько картинок из "Ветвящихся объёмов", которые правда очень люблю:
Victor Kleptsyn
14:27
In reply to this message
Алгебраическая функция = её график = полиномиальное соотношение "F(x,z)=0" вместо обычного "z=f(x)".
Victor Kleptsyn
14:31
А что происходит в точке, где у графика вертикальная касательная, и два прообраза сливаются (как в точке c_3 на предыдущем рисунке)? Простейший случай — функция "квадратный корень", или x-z^2=0. В саму точку заходить не будем — зато выйдем в комплексные числа, и обойдём вокруг.
Victor Kleptsyn
14:38
Монодромия при обходе вокруг особой точки c: подошли, обошли вокруг, вернулись. По любому пути мы бы получили какую-то перестановку значений (с графика мы всё равно никуда не делись); по такому — меняем два значения местами (B и C), те самые, которые сливаются при подходе к c. Ибо остальные (A) там проблем не чувствуют, а у B и C поведение такое же, как на предыдущем рисунке.
Victor Kleptsyn
14:49
Начальный ход доказательства — смотрим вообще только на секущие одного направления (развернув систему координат — на {x=c}). Только направления такого, чтобы касания в крайних точках были бы квадратичными, а не более высокого порядка (теоретически, например, там могло бы быть уплощение как для x=y^4).
Victor Kleptsyn
14:57
Но можно обходить не только вокруг минимума m, но и вокруг максимума M.
При подходе к M на площадь можно смотреть как на константу (площадь всего овала!) минус площадь "белой" луночки. А площадь белой луночки при обходе вокруг M меняет знак. Значит, после обхода будет площадь всего овала плюс площадь луночки у M.
Но дальше — уже обойдя M — можно пойти к минимуму m. Где мы посмотрим на результат до обхода как на 2x(площадь всего овала) минус площадь луночки у m. После обхода m — минус меняется на плюс, и мы получили 2x(площадь всего овала)+луночку у m.
При подходе к M на площадь можно смотреть как на константу (площадь всего овала!) минус площадь "белой" луночки. А площадь белой луночки при обходе вокруг M меняет знак. Значит, после обхода будет площадь всего овала плюс площадь луночки у M.
Но дальше — уже обойдя M — можно пойти к минимуму m. Где мы посмотрим на результат до обхода как на 2x(площадь всего овала) минус площадь луночки у m. После обхода m — минус меняется на плюс, и мы получили 2x(площадь всего овала)+луночку у m.
Victor Kleptsyn
15:04
In reply to this message
То есть, обойдя сначала вокруг M, потом вокруг m, мы к исходному отсекаемому объёму V(c) прибавили константу: удвоенную полную площадь всего овала (2V_0).
Тогда, если сделать такой парный обход ещё раз, то мы добавим ещё столько же, те же 2V_0; например, потому, что продолжение 2V_0 + V(c) это всё равно, что константа 2V_0 плюс продолжение V(c).
Сделав парный обход ещё раз — добавим ещё столько же, и продолжать так можно неограниченно.
Но это как раз противоречит алгебраичности отсекаемой площади V(c) — если бы она была алгебраической, то любому c можно было бы сопоставить лишь конечное число значений — корней полинома P(c,V)=0, который задаёт "график" V(c). А у нас этих значений счётное число (потому что "парных обходов" можно сделать сколько угодно) — вот и получилось противоречение, которое доказывает теорему Ньютона.
Тогда, если сделать такой парный обход ещё раз, то мы добавим ещё столько же, те же 2V_0; например, потому, что продолжение 2V_0 + V(c) это всё равно, что константа 2V_0 плюс продолжение V(c).
Сделав парный обход ещё раз — добавим ещё столько же, и продолжать так можно неограниченно.
Но это как раз противоречит алгебраичности отсекаемой площади V(c) — если бы она была алгебраической, то любому c можно было бы сопоставить лишь конечное число значений — корней полинома P(c,V)=0, который задаёт "график" V(c). А у нас этих значений счётное число (потому что "парных обходов" можно сделать сколько угодно) — вот и получилось противоречение, которое доказывает теорему Ньютона.
Victor Kleptsyn
М
15:19
Математические байки
Для невыпуклых областей на плоскости (опять-таки, с алгебраической бесконечно гладкой границей) проходит аналогичное рассуждение — только крутиться приходится больше.
Victor Kleptsyn
15:23
In reply to this message
И дальше уже без проблем можно дойти до m=p_1, после чего, обойдя, пуститься в обратный путь...
Victor Kleptsyn
М
15:39
Математические байки
In reply to this message
А это объяснение того, почему в невыпуклом случае, начав движение из лунки рядом с минимумом на одной стороне, всегда получится прийти в лунку рядом с максимумом. А именно — самое важное в отрезаемой площади это отрезок, на который она опирается. Ну а если нарисовать множество возможных пар "первая точка, вторая точка", то это будет много замкнутых кривых + ровно одна кривая с двумя концами. Один из которых отвечает лунке над минимумом m, а другой — лунке над максимумом M. Просто потому, что нигде больше такая кривая не обрывается —
Victor Kleptsyn
15:52
Ну и последняя пара картинок — иллюстрации к теореме Пикара-Лефшеца, здесь — в простейшем случае. Пусть мы смотрим на множество P(z,w)=c, где z и w — комплексные; соответственно, это с вещественной точки зрения двумерная поверхность.
Если мы двигаем c, не заходя в критические значения P — то поверхность двигается "по чуть-чуть". А что будет, если мы захотим "обойти" вокруг критического значения? Например, если на поверхности нарисована замкнутая кривая, и она заходит в окрестность соответствующей критической точки — логично ожидать, что она как-то перестроится. А как?
Если мы двигаем c, не заходя в критические значения P — то поверхность двигается "по чуть-чуть". А что будет, если мы захотим "обойти" вокруг критического значения? Например, если на поверхности нарисована замкнутая кривая, и она заходит в окрестность соответствующей критической точки — логично ожидать, что она как-то перестроится. А как?
Victor Kleptsyn
М
16:08
Математические байки
In reply to this message
Ответ такой. Для простоты будем считать, что критическое значение это c=0. С комплексной точки зрения все невырожденные критические точки одинаковые (с точностью до локальной замены координат) — так выберем локальные координаты (z',w') так, чтобы в них.
P(z',w')=z'w'.
Тогда при малых c рядом с критическим значением поверхность уровня устроена как цилиндр. Так вот — этот цилиндр скручивается:
P(z',w')=z'w'.
Тогда при малых c рядом с критическим значением поверхность уровня устроена как цилиндр. Так вот — этот цилиндр скручивается:
Victor Kleptsyn
16:18
Потому что если c бежит по окружности радиуса ε,
c(t) = ε e^{it},
то мы хотим как-то двигать z и w так, чтобы далеко от критической точки (то есть если либо |z|, либо |w| большие) за полный оборот вообще ничего не произошло.
Ну так давайте двигать окружности вида |z|=r с постоянной скоростью, деля множитель e^{it} в каком-то отношении между z и w:
z(t)=z(0) e^{i f(r) t}
w(t)=w(0) e^{i (1-f(r)) t}
c(t) = ε e^{it},
то мы хотим как-то двигать z и w так, чтобы далеко от критической точки (то есть если либо |z|, либо |w| большие) за полный оборот вообще ничего не произошло.
Ну так давайте двигать окружности вида |z|=r с постоянной скоростью, деля множитель e^{it} в каком-то отношении между z и w:
z(t)=z(0) e^{i f(r) t}
w(t)=w(0) e^{i (1-f(r)) t}
Victor Kleptsyn
16:22
In reply to this message
Если мы попросим, чтобы f(r) = 0 при больших r=|z| (например, при r>2 \sqrt{ε}) и чтобы 1-f(r)=0 при больших ε/r=|w| (например, при r<\sqrt{ε}/2) — как раз вот такое скручивание и получится.
Victor Kleptsyn
16:34
Вот. Ну и мне кажется, что это безумно круто, что вся эта наука возникает не просто так, повисая в воздухе — а естественно появляется, шаг за шагом, при атаке на вполне разумные геометрические (восходящие к Ньютону и к Арнольду) вопросы. И что всё это очень геометрично и за этим можно (и очень приятно) следить. И что в тексте получается дойти и рассказать доказательство полного результата для чётномерного случая, — того самого, который Васильев доказал после ЛШСМ-2013: V. A. Vassiliev, Newton's lemma XXVIII on integrable ovals in higher dimensions and reflection groups, Bulletin of the London Mathematical Society.
Я очень люблю эту книгу. 🙂
Я очень люблю эту книгу. 🙂
Victor Kleptsyn
М
19:15
Математические байки
Н
Непрерывное математическое образование 11.04.2021 14:25:33
https://twitter.com/fermatslibrary/status/1373631751898157061
картинка по выходным: неравенство между средним арифметическим и средним геометрическим
картинка по выходным: неравенство между средним арифметическим и средним геометрическим
Victor Kleptsyn
М
19:25
Математические байки
In reply to this message
Да, коллеги пожаловались, что непонятно, почему вторая, третья и так далее пары обходов вокруг m и M будут добавлять ту же константу — так что я отредактировал это сообщение. По смыслу — если в результате продолжения функции V(c) по какому-то пути мы пришли к V(c)+const, то дальше по тому же пути можно аналитически продолжать слагаемые по отдельности. Продолжение V(c) даёт V(c)+const, а продолжение константы это она и есть. Так что получается V(c)+2*const. И так далее.
(Кстати — так ведёт себя комплексный логарифм ln z: набирает 2πi за каждый обход вокруг нуля в положительном направлении.)
Надеюсь, теперь стало понятнее.
(Кстати — так ведёт себя комплексный логарифм ln z: набирает 2πi за каждый обход вокруг нуля в положительном направлении.)
Надеюсь, теперь стало понятнее.
Victor Kleptsyn
12 April 2021
М
11:14
Математические байки
In reply to this message
И я пользуюсь случаем присоединиться к Васильеву и сказать "огромное спасибо" Ане Роговой — без её расшифровки просто ничего бы не запустилось...
Victor Kleptsyn
11:20
In reply to this message
===
Оказывается — спасибо Александру Шпилькину за рассказ и за ссылки! — у этого анекдота есть продолжение: вычисление интеграла \int_0^1 x^m (1-x)^n dx:
Оказывается — спасибо Александру Шпилькину за рассказ и за ссылки! — у этого анекдота есть продолжение: вычисление интеграла \int_0^1 x^m (1-x)^n dx:
Victor Kleptsyn
11:31
In reply to this message
Но давайте я сначала напомню, как с этим интегралом работают обычно. Первый шаг тут это замечание, что у факториала есть обобщение, гамма-функция; мы с ней уже сталкивались, когда обсуждали формулу Стирлинга. А именно, факториал можно представить как интеграл —
n! = \int_0^{\infty} x^n e^{-x} dx —
после чего ничего не мешает в этом интеграле брать нецелое значение степени:
Г(a) := \int_0^{\infty} x^{a-1} e^{-x} dx,
и тогда n!=Г(n+1).
n! = \int_0^{\infty} x^n e^{-x} dx —
после чего ничего не мешает в этом интеграле брать нецелое значение степени:
Г(a) := \int_0^{\infty} x^{a-1} e^{-x} dx,
и тогда n!=Г(n+1).
Victor Kleptsyn
11:35
Так вот — интеграл B(a,b):=\int_0^1 x^{a-1} (1-x)^{b-1} dx называется бета-функцией, и он через гамма-функцию явным образом выражается:
Victor Kleptsyn
11:47
И доказательство тут — перемножить два интеграла, для Г(a) и для Г(b). Получится интеграл по первому квадранту {x>0,y>0} — который нарезается на диагональные отрезки {x+y=s}, после чего интеграл оказывается произведением Г(a+b) и интеграла для бета-функции:
Victor Kleptsyn
М
15:19
Математические байки
In reply to this message
Так вот — давайте отставим все эти интегралы в сторону и добудем ответ (для целых аргументов a=m+1 и b=n+1) вероятностными методами. А именно — выберем на отрезке [0,1] равномерно случайную точку x. А потом ещё m случайных точек \xi_1,...,\xi_m. А потом ещё n случайных точек \eta_1,...,\eta_n.
И посмотрим вот на такое событие: все \xi_1,...,\xi_m попали на отрезок [0,x], а все \eta_1,...,\eta_n — на отрезок [x,1]:
И посмотрим вот на такое событие: все \xi_1,...,\xi_m попали на отрезок [0,x], а все \eta_1,...,\eta_n — на отрезок [x,1]:
Victor Kleptsyn
15:20
Чему равна его вероятность? С одной стороны, при известном x это как раз x^m*(1-x)^n, а поскольку точка x тоже кидалась равномерно — то получается как раз искомый интеграл:
\int_0^1 x^m (1-x)^n dx.
\int_0^1 x^m (1-x)^n dx.
Victor Kleptsyn
15:27
In reply to this message
С другой стороны, все случайные величины x,\xi_1,...,\xi_m,\eta_1,...,\eta_n — совершенно равноправны. А мы хотим, чтобы раскраска "первые m по величине в красный цвет, m+1-я в чёрный, оставшиеся n в синий" совпала бы с раскраской "x в чёрный цвет, \xi_i в красный, \eta_j в синий". То есть вероятность это 1/число таких раскрасок. А число таких раскрасок — это мультиномиальный коэффициент: число способов разбить (m+n+1) элемент на группы из m, n и 1 элемента, которое равно (m+n+1)!/(m!*n!).
Вот мы и получили, что интеграл
\int_0^1 x^m (1-x)^n dx
равен
m!*n!/(m+n+1)!
Вот мы и получили, что интеграл
\int_0^1 x^m (1-x)^n dx
равен
m!*n!/(m+n+1)!
Victor Kleptsyn
13 April 2021
М
09:55
Математические байки
t
tropical saint petersburg 12.04.2021 13:10:07
у обычного маятника есть устойчивое равновесие, когда он висит вертикально вниз, и неустойчивое — вертикально вверх, когда любое движение выводит его из равновесия. Оказывается, если точку подвеса маятника мелко и быстро колебать, то появится равновесие с маятником торчащим вверх. Отличное видео с объяснением и примерами. Тут текстом (малопонятно), более или менее копия с Кванта.
А вот статья Капицы:
"Естественно, что ни одной из механических систем не было уделено столько внимания и всестороннего теоретического изучения как всем разновидностям движения маятника. Казалось бы, что за 300 лет, прошедших со времён Галилея, этот вопрос должен был быть исчерпан и если что-либо оставалось для изучения, то это должно было носить характер дошлифовки ранее полученных результатов. Но, повидимому, тому типу движения маятника, которому посвящена эта статья, не было уделено достаточно внимания и одна из очень своеобразных и интересных разновидностей колебаний маятника осталась почти полностью не изученной. Обратить внимание на этот тип движения и на открывающиеся при его изучении возможности и ставит себе целью эта статья." Но видео лучше!
А вот статья Капицы:
"Естественно, что ни одной из механических систем не было уделено столько внимания и всестороннего теоретического изучения как всем разновидностям движения маятника. Казалось бы, что за 300 лет, прошедших со времён Галилея, этот вопрос должен был быть исчерпан и если что-либо оставалось для изучения, то это должно было носить характер дошлифовки ранее полученных результатов. Но, повидимому, тому типу движения маятника, которому посвящена эта статья, не было уделено достаточно внимания и одна из очень своеобразных и интересных разновидностей колебаний маятника осталась почти полностью не изученной. Обратить внимание на этот тип движения и на открывающиеся при его изучении возможности и ставит себе целью эта статья." Но видео лучше!
Victor Kleptsyn
М
09:57
Математические байки
И я сразу добавлю восьмиминутную запись рассказа Арнольда про ту же историю — с демонстрацией той самой электробритвы с перевёрнутым маятником в конце: https://etudes.ru/etudes/arnold-pendulum/
Victor Kleptsyn
М
10:36
Математические байки
In reply to this message
Продолжим?
Мы посчитали этот интеграл вероятностными методами. Но тут остаются два вопроса.
Во-первых: мы начали с того, что
n! = Г(n+1) = \int_0^{\infty} x^n e^{-x} dx.
А почему это так? Можно (и несложно!) доказать это просто по индукции — интегрированием по частям; но может быть, есть ещё какое-то объяснение?
Во-вторых: для вычисления исходного интеграла у нас теперь есть два способа — "вероятностный" и "классический". А нельзя ли их как-то объединить? Оказывается, что можно!
Но и для того, и для другого нам потребуется новый объект, пуассоновский процесс.
Мы посчитали этот интеграл вероятностными методами. Но тут остаются два вопроса.
Во-первых: мы начали с того, что
n! = Г(n+1) = \int_0^{\infty} x^n e^{-x} dx.
А почему это так? Можно (и несложно!) доказать это просто по индукции — интегрированием по частям; но может быть, есть ещё какое-то объяснение?
Во-вторых: для вычисления исходного интеграла у нас теперь есть два способа — "вероятностный" и "классический". А нельзя ли их как-то объединить? Оказывается, что можно!
Но и для того, и для другого нам потребуется новый объект, пуассоновский процесс.
Victor Kleptsyn
М
10:53
Математические байки
Процесс совершенно естественный, на самом деле. А именно: представим себе, что у нас лежит большой кусок радиоактивного вещества — и рядом стоит счётчик Гейгера, соединённый с самописцем. Каждый раз, когда счётчик засекает распад — самописец ставит точку-отметку на ленте. В результате на ленте получается — случайный! — набор точек:
Victor Kleptsyn
М
14:15
Математические байки
In reply to this message
Этот случайный набор точек это и есть пуассоновский [точечный] процесс [на прямой]; давайте посмотрим, что о нём можно сказать.
Самое важное — это что количества (и расположения) точек на непересекающихся отрезках времени независимы; если у нас не было распадов за первую секунду — это никак не влияет на то, что будет во вторую, в третью, и так далее.
Самое важное — это что количества (и расположения) точек на непересекающихся отрезках времени независимы; если у нас не было распадов за первую секунду — это никак не влияет на то, что будет во вторую, в третью, и так далее.
Victor Kleptsyn
14:18
Можно сказать, что каждый отдельный атом за каждую микроскопическую долю времени подкидывает монетку с очень-очень-очень маленькой вероятностью, решая, распасться ли ему. Как мы знаем, предыдущие результаты подбрасываний на следующие не влияют; поэтому много-много "решек", которые выбросили все выжившие атомы, никак не влияют на то, как они будут жить дальше. Единственная тонкость, это что те атомы, которые распались, дальше не участвуют — но пока их счёт идёт на единицы, а образец у нас макроскопический (а число Авогадро 6.02*10^23), этим можно спокойно пренебречь.
Victor Kleptsyn
14:19
Пусть λ — среднее число распадов в единицу времени; его называют интенсивностью процесса. Как устроено распределение (случайного) числа отметок (распадов атомов) на отрезке времени от 0 до 1?
Victor Kleptsyn
М
14:47
Математические байки
Поделим этот отрезок времени на очень большое число N частей (пусть 1/N это просто временное разрешение нашего самописца) — так, чтобы вероятностью получить два распада на одном отрезке можно было бы пренебречь. Тогда на каждом отрезке мы подкидываем монетку, на которой "есть распад" выпадает с очень маленькой вероятностью λ/N, и "нет распада" с оставшейся.
Поэтому, например, вероятность того, что не было ни одного распада, равна (1-λ/N)^N, что при N->\infty стремится к e^{-λ}.
Поэтому, например, вероятность того, что не было ни одного распада, равна (1-λ/N)^N, что при N->\infty стремится к e^{-λ}.
Victor Kleptsyn
14:48
А если мы будем смотреть не на отрезке длины 1, а на отрезке времени длины t — то вероятность будет e^{-λt}.
Victor Kleptsyn
14:58
К фиксированному отрезку мы сейчас вернёмся — но вообще отсюда можно увидеть, что мы можем сказать про (случайный, как и всё остальное) момент первого распада T_1: вероятность того, что T_1>t, равна e^{-λt}.
Это — экспоненциальное распределение с параметром λ. Оно обладает тем (естественно возникающим из независимости подбрасываний монетки) свойством, что если мы его ждём и за какое-то время t_0 оно ещё не произошло — то при этом условии распределение оставшегося времени ожидания такое же, каким распределение T_1 было исходно. Очень неприятно ждать автобус, если у него такое распределение времени прихода: вроде как ждали-ждали, а если он ещё не пришёл, то ждать остаётся (в смысле распределения) "столько же"!
Это — экспоненциальное распределение с параметром λ. Оно обладает тем (естественно возникающим из независимости подбрасываний монетки) свойством, что если мы его ждём и за какое-то время t_0 оно ещё не произошло — то при этом условии распределение оставшегося времени ожидания такое же, каким распределение T_1 было исходно. Очень неприятно ждать автобус, если у него такое распределение времени прихода: вроде как ждали-ждали, а если он ещё не пришёл, то ждать остаётся (в смысле распределения) "столько же"!
Victor Kleptsyn
14:59
In reply to this message
(Да, тут коллеги ругаются на то, что на картинке выше точки слишком посередине каждого отрезка — так что вот улучшенная непрерывная версия!)
Victor Kleptsyn
М
15:57
Математические байки
In reply to this message
А с какой вероятностью у нас на этом отрезке будет отмечен ровно один распад? У нас N "делений времени", на которых он может произойти; на каждом вероятность, что он произойдёт, это (λ/N), да ещё нужно домножить на вероятность, что больше нигде распадов не будет, (1-λ/N)^{N-1}. Итого
Victor Kleptsyn
М
16:53
Математические байки
Ну и вообще, если нас интересует, с какой вероятностью на отрезке [0,1] произошло ровно k распадов — то нужно выбрать места, где они происходят, а это можно сделать C_N^k способами, и умножить это на вероятность каждой отдельной "конфигурации": k распадов (с вероятностью (λ/N) каждый) и N-k не-распадов. Итого получаем:
Victor Kleptsyn
16:53
Потому что последний сомножитель это так и есть примерно e^{-λ}, а произведение первых двух можно переписать:
Victor Kleptsyn
16:55
In reply to this message
И все сомножители в правой части, кроме первого, это почти 1.
Victor Kleptsyn
14 April 2021
М
14:48
Математические байки
Итак, мы (чуть-чуть рукомахательно — переходя к пределу при N->\infty) выяснили, что вероятность получить k=0,1,2,... распадов за время 1 равна
p_k = (1/k!) λ^k e^{-λ}.
Определение. Такое распределение называется пуассоновским с параметром λ (и обозначается π(λ)).
И вот отсюда пуассоновское распределение вообще появляется — как распределение "редких событий" — числа успехов в большом-большом числе испытаний, каждое из которых даёт очень маленький вклад, а в среднем получается λ. Стандартный пример из учебника — число запросов за минуту к АТС, если абонентов много, а каждый отдельный абонент решает позвонить именно сейчас с довольно небольшой вероятностью.
p_k = (1/k!) λ^k e^{-λ}.
Определение. Такое распределение называется пуассоновским с параметром λ (и обозначается π(λ)).
И вот отсюда пуассоновское распределение вообще появляется — как распределение "редких событий" — числа успехов в большом-большом числе испытаний, каждое из которых даёт очень маленький вклад, а в среднем получается λ. Стандартный пример из учебника — число запросов за минуту к АТС, если абонентов много, а каждый отдельный абонент решает позвонить именно сейчас с довольно небольшой вероятностью.
Victor Kleptsyn
15:03
Кстати — пуассоновский процесс можно рассматривать и не только на прямой. Скажем, представим себе, что наш радиоактивный материал как-то размещён на столе — а мы по прошествии минуты (или часа) отмечаем положения распавшихся атомов (не будем задумываться, как это можно реализовать технически). Тогда мы получим конечный набор точек — такой, что для маленького кусочка стола вероятность того, что точка там есть, это примерно масса лежащего там вещества*среднее число распадов на единицу массы за выбранный интервал времени.
И дальше можно либо опять разрезать стол на маленькие кусочки — или сказать, что для непересекающихся областей расположения точек в них независимы, а количество точек в области A распределено по Пуассону с параметром "масса вещества в A*среднее число распадов за данное время на единицу массы". И ровно так работает общее определение пуассоновского процесса, построенного по неатомарной мере μ — где мы говорим, что число точек в области A распределено как π(μ(A)), а для непересекающихся областей подмножества в них независимы.
И дальше можно либо опять разрезать стол на маленькие кусочки — или сказать, что для непересекающихся областей расположения точек в них независимы, а количество точек в области A распределено по Пуассону с параметром "масса вещества в A*среднее число распадов за данное время на единицу массы". И ровно так работает общее определение пуассоновского процесса, построенного по неатомарной мере μ — где мы говорим, что число точек в области A распределено как π(μ(A)), а для непересекающихся областей подмножества в них независимы.
Victor Kleptsyn
15:13
Вернёмся к одномерному процессу. Ещё одна вещь, которую мне про него хочется сказать, это что на него (как раз благодаря его одномерности) можно смотреть двумя разными способами: можно так, как мы описали, спрашивая, "сколько отметок в данном интервале". А можно — смотреть на расстояния между отметками (разности между последовательными точками): первая отметка в (случайный) момент T_1=x_1, второй после первой надо ждать второй случайное время T_2=x_2-x_1, ... — и все T_j независимы (ибо то, что уже распалось/не распалось, на то, что будет дальше, не влияет) и распределены как экспоненциальные с параметром λ: вероятность, что T_j больше t, это e^{-λt}.
Victor Kleptsyn
15:14
In reply to this message
А теперь — после всех этих блужданий (но, надеюсь, что-то интересное выяснив по пути), давайте вернёмся к исходным вопросам. И начнём с первого из них — как можно объяснить, что
n! = \int_0^{\infty} x^n e^{-x} dx ?
n! = \int_0^{\infty} x^n e^{-x} dx ?
Victor Kleptsyn
15:21
In reply to this message
Давайте на n! поделим. Получим тожество
\int_0^{\infty} (1/n!) x^n e^{-x} dx = 1.
А здесь уже явно прослеживается теория вероятностей! Если интеграл чего-то неотрицательного равен 1 — это должна быть плотность распределения какой-то случайной величины. А какой?
На самом деле — мы уже видели почти то, что нам нужно, только с заменой x на λ и n на k. И ещё это была не плотность, а вероятность. Ну да сейчас допилим!
\int_0^{\infty} (1/n!) x^n e^{-x} dx = 1.
А здесь уже явно прослеживается теория вероятностей! Если интеграл чего-то неотрицательного равен 1 — это должна быть плотность распределения какой-то случайной величины. А какой?
На самом деле — мы уже видели почти то, что нам нужно, только с заменой x на λ и n на k. И ещё это была не плотность, а вероятность. Ну да сейчас допилим!
Victor Kleptsyn
15:24
А именно — пусть у нас пуассоновский процесс с единичной интенсивностью. Давайте посмотрим на плотность распределения (k+1)-го по порядку момента распада. Так вот, это в точности
ρ(x)=(1/n!) x^n e^{-x}.
Потому что — чтобы (k+1)-й распад попал в маленький отрезок от x до x+dx, нужно, чтобы
1) в этом отрезке распад произошёл — вот отсюда вероятность dx
2) до того распадов было ровно k — а вот отсюда всё остальное.
ρ(x)=(1/n!) x^n e^{-x}.
Потому что — чтобы (k+1)-й распад попал в маленький отрезок от x до x+dx, нужно, чтобы
1) в этом отрезке распад произошёл — вот отсюда вероятность dx
2) до того распадов было ровно k — а вот отсюда всё остальное.
Victor Kleptsyn
М
16:03
Математические байки
Вот мы ответ на первый вопрос и получили: (1/n!) x^n e^{-x} это плотность распределения n+1-й точки для пуассоновского процесса единичной интенсивности — и поэтому (полная вероятность!) совершенно естественно, что интеграл от неё равен 1.
Кстати — если мы k+1-ю точку x_{k+1} мы знаем, то при этом условии набор предыдущих точек получается таким же, как если бы мы на отрезок [0,x_{k+1}] равномерно кинули k независимых точек, а потом бы их упорядочили по возрастанию (вот, кстати, ещё один способ увидеть факториал в знаменателе). Например, потому что при делении на N интервалов и при подкидывании соответствующих монеток все конфигурации "k успехов, N-k неудач" равноправны.
Кстати — если мы k+1-ю точку x_{k+1} мы знаем, то при этом условии набор предыдущих точек получается таким же, как если бы мы на отрезок [0,x_{k+1}] равномерно кинули k независимых точек, а потом бы их упорядочили по возрастанию (вот, кстати, ещё один способ увидеть факториал в знаменателе). Например, потому что при делении на N интервалов и при подкидывании соответствующих монеток все конфигурации "k успехов, N-k неудач" равноправны.
Victor Kleptsyn
М
20:29
Математические байки
In reply to this message
Теперь начинает проявляться и ответ на второй вопрос: как связаны "классический" и "вероятностный" способы смотреть на вычисление бета-функции?
А именно — давайте в начале классического доказательства поделим оба интеграла на соответствующие факториалы (точнее, пока ещё на гамма-функции):
А именно — давайте в начале классического доказательства поделим оба интеграла на соответствующие факториалы (точнее, пока ещё на гамма-функции):
Victor Kleptsyn
20:31
В правой части написано совместная плотность для двух независимых случайных величин; одна с плотностью (1/Г(a)) x^{a-1} e^{-x},
Victor Kleptsyn
20:32
другая — с такой же с заменой a на b. Да — такие распределения (логично) называются гамма-распределениями.
Victor Kleptsyn
М
21:12
Математические байки
Так вот, когда мы этот интеграл считали, мы нарезали всё на отрезки x+y=s. И оказывалось, что интеграл по одному такому отрезку — это
s^{a+b-1}*B(a,b)/(Г(a)Г(b)).
А второе интегрирование тогда даёт
Г(a+b)*B(a,b)/(Г(a)Г(b)),
и из равенства 1 и получается искомый ответ.
Так вот, на вероятностном языке это переговаривается так:
1) свёртка двух гамма-распределений (a.k.a. распределение суммы независимых случайных величин с такими распределениями) — это гамма-распределение с суммой параметров. Потому что мы, собственно, и получили плотность для s=x+y как гамма-распределение с параметром a+b.
2) условное распределение x при условии x+y=s — это растянутое в s раз одно и то же бета-распределение на отрезке [0,1]: распределение на отрезке [0,1] с плотностью
1/B(a,b) x^{a-1} (1-x).
s^{a+b-1}*B(a,b)/(Г(a)Г(b)).
А второе интегрирование тогда даёт
Г(a+b)*B(a,b)/(Г(a)Г(b)),
и из равенства 1 и получается искомый ответ.
Так вот, на вероятностном языке это переговаривается так:
1) свёртка двух гамма-распределений (a.k.a. распределение суммы независимых случайных величин с такими распределениями) — это гамма-распределение с суммой параметров. Потому что мы, собственно, и получили плотность для s=x+y как гамма-распределение с параметром a+b.
2) условное распределение x при условии x+y=s — это растянутое в s раз одно и то же бета-распределение на отрезке [0,1]: распределение на отрезке [0,1] с плотностью
1/B(a,b) x^{a-1} (1-x).
Victor Kleptsyn
М
21:53
Математические байки
In reply to this message
Так вот — возвращаясь к случаю, когда a=m+1 и b=n+1 целые. В этом случае x распределено как m+1-я точка в пуассоновском процессе с единичной интенсивностью, а y — как n+1-я.
Victor Kleptsyn
21:54
In reply to this message
Но тогда s=x+y и впрямь распределено как m+n+2-я точка; и чему бы ни равнялось s — условное распределение первых m+n+1-й точки, как мы уже видели, такое же, как при "равномерном бросании" (только нужно упорядочить набор).
Victor Kleptsyn
15 April 2021
М
14:29
Математические байки
In reply to this message
И вот ответ на второй вопрос о том, как связаны два взгляда: в классическом подходе тот интеграл, который возникает после замены и перехода на отрезок [0,1] — это (спасибо пуассоновскому взгляду) интеграл от плотности, которую мы получаем для распределения m+1-й по возрастанию точки из m+n+1 равномерно и независимо выбираемых. А эта плотность пропорциональна x^m*(1-x)^n, с коэффициентом пропорциональности, равном числу вариантов "меньшие m точек, m+1-я, большие n",
(m+n+1)!/(m! n!) —
и это и есть наше исходное вероятностное рассуждение.
(m+n+1)!/(m! n!) —
и это и есть наше исходное вероятностное рассуждение.
Victor Kleptsyn
М
14:57
Математические байки
P.S. Ссылки к этому рассказу — https://math.stackexchange.com/a/3540 + https://math.stackexchange.com/a/3498 ; за них ещё раз спасибо Александру Шпилькину.
Ещё пара замечаний в заключение. Во-первых, пуассоновский процесс (по конечной мере μ на любом множестве X) можно строить ещё так: сначала решить, сколько всего M точек будет, "кинув пуассоновский кубик" с параметром μ(X), а потом выбрать в X равномерно по нормированной мере (1/μ(X))μ эти M точек независимо друг от друга.
А если мера только локально-конечная (как мера Лебега на прямой или на луче [0,\infty)), то можно разрезать пространство на кусочки конечной меры и применить эту конструкцию в них по отдельности. (Кстати, не-атомарность меры тут уже не требуется, если мы готовы для атомов говорить, что в них выбирается больше одной точки.)
И — история, за которую спасибо @qtasep. Вообще, если мы возьмём квадрат [0,1]^2 и накидаем в него довольно точек (можно сказать, запустив пуассоновский процесс, а можно — сначала решить, сколько именно их будет, а потом просто выбрать такое количество точек независимо и равномерно) — они будут расположены, "на глаз", довольно неравномерно (просто потому, что где-нибудь да будет зона, где выпало побольше, а где-то поменьше; это, наоборот, идеальная равномерность пуассоновскому вытаскиванию противоречила бы). Вот пример такого "накидывания равномерно-независимых точек" (здесь их 100) :
Ещё пара замечаний в заключение. Во-первых, пуассоновский процесс (по конечной мере μ на любом множестве X) можно строить ещё так: сначала решить, сколько всего M точек будет, "кинув пуассоновский кубик" с параметром μ(X), а потом выбрать в X равномерно по нормированной мере (1/μ(X))μ эти M точек независимо друг от друга.
А если мера только локально-конечная (как мера Лебега на прямой или на луче [0,\infty)), то можно разрезать пространство на кусочки конечной меры и применить эту конструкцию в них по отдельности. (Кстати, не-атомарность меры тут уже не требуется, если мы готовы для атомов говорить, что в них выбирается больше одной точки.)
И — история, за которую спасибо @qtasep. Вообще, если мы возьмём квадрат [0,1]^2 и накидаем в него довольно точек (можно сказать, запустив пуассоновский процесс, а можно — сначала решить, сколько именно их будет, а потом просто выбрать такое количество точек независимо и равномерно) — они будут расположены, "на глаз", довольно неравномерно (просто потому, что где-нибудь да будет зона, где выпало побольше, а где-то поменьше; это, наоборот, идеальная равномерность пуассоновскому вытаскиванию противоречила бы). Вот пример такого "накидывания равномерно-независимых точек" (здесь их 100) :
Victor Kleptsyn
М
16:07
Математические байки
In reply to this message
Так вот — представьте себе примерно такую картину — но наложенную на карту Лондона. И представьте себе, что на дворе 1944-й год, а точки — это места падения (и взрыва!) "Фау". И явно видны, то здесь, то там, кластеры из близких попаданий. А у вас спрашивают — "эти кластеры, это немцы туда целятся [и, возможно, их ракеты умеют донаводиться на финальном участке траектории?], или это случайность?"
Статья R. D. Clarke 1946 года (одностраничная!) — как раз о том, как они проводили такой анализ (кстати, об этом есть рассказ в Britannica). Наложили на Лондон разумно-мелкую сетку — разделили область 12x12 км на 576=24^2 квадратов со стороной 0.5 км. И посмотрели, сколько из 537 бомб попали в какой квадрат — и сколько квадратов с 1, 2, 3, ... попаданиями. После чего оказалось, что соответствующие количества очень похожи на те, которые получались бы для пуассоновского распределения (то есть для равномерно-случайной стрельбы).
Статья R. D. Clarke 1946 года (одностраничная!) — как раз о том, как они проводили такой анализ (кстати, об этом есть рассказ в Britannica). Наложили на Лондон разумно-мелкую сетку — разделили область 12x12 км на 576=24^2 квадратов со стороной 0.5 км. И посмотрели, сколько из 537 бомб попали в какой квадрат — и сколько квадратов с 1, 2, 3, ... попаданиями. После чего оказалось, что соответствующие количества очень похожи на те, которые получались бы для пуассоновского распределения (то есть для равномерно-случайной стрельбы).
Victor Kleptsyn
16 April 2021
М
11:59
Математические байки
И последнее — ещё пара картинок в заключение ко вчерашнему рассказу:
1) http://www.empiricalzeal.com/wp-content/uploads/2012/12/pinker-glow-worms-and-stars-plot.jpg : слева — случайно раскиданные точки, справа — положения светящихся glowworms на своде пещеры Waitomo в Новой Зеландии (источник — "What does randomness look like?", Wired). Последние светом приманивают пищу — так что им прямой резон располагаться подальше друг от друга, чтобы не мешать друг другу охотиться.
1) http://www.empiricalzeal.com/wp-content/uploads/2012/12/pinker-glow-worms-and-stars-plot.jpg : слева — случайно раскиданные точки, справа — положения светящихся glowworms на своде пещеры Waitomo в Новой Зеландии (источник — "What does randomness look like?", Wired). Последние светом приманивают пищу — так что им прямой резон располагаться подальше друг от друга, чтобы не мешать друг другу охотиться.
Victor Kleptsyn
12:03
2) картинка из статьи "Determinantal Processes and Independence", J. Ben Hough, Manjunath Krishnapur, Yuval Peres, Bálint Virág: слева-сверху пуассоновский процесс ( = случайное распределение точек), справа-сверху — детерминантный (точки "отталкиваются" друг от друга), снизу в центре — перманентный (точки "комкуются"); спасибо @qtasep за ссылку!
Victor Kleptsyn
18 April 2021
М
18:09
Математические байки
Н
Непрерывное математическое образование 18.04.2021 17:40:35
На витрине ювелирного магазина лежат 15 бриллиантов. Рядом с ними стоят таблички с указанием масс, на которых написано 1, 2, ..., 15 карат. У продавца есть чашечные весы и четыре гирьки массами 1, 2, 4 и 8 карат. Покупателю разрешается только один тип взвешиваний: положить один из бриллиантов на одну чашу весов, а гирьки — на другую и убедиться, что масса на соответствующей табличке указана верно. Однако за каждую взятую гирьку нужно заплатить продавцу 100 монет. Если гирька снимается с весов и в следующем взвешивании не участвует, продавец забирает её. Какую наименьшую сумму придётся заплатить, чтобы проверить массы всех бриллиантов?
вот такую, например, задачу А.В.Грибалко с сегодняшнего МатПраздника предлагается решить
(потом можно также прочитать в брошюре небольшой комментарий про контекст)
вот такую, например, задачу А.В.Грибалко с сегодняшнего МатПраздника предлагается решить
(потом можно также прочитать в брошюре небольшой комментарий про контекст)
Victor Kleptsyn
М
18:12
Математические байки
In reply to this message
Присоединюсь к коллегам: задача очень хорошая, а послесловие про контекст действительно стоит посмотреть!
Victor Kleptsyn
19 April 2021
М
14:50
Математические байки
Это, конечно, оффтопик для этого канала — но поздравляю всех с первым аппаратом тяжелее атмосферы, аэродинамически поднявшимся в воздух на другой планете!
Формулировка про "тяжелее воздуха" тут точная — в атмосфере Венеры летали (надувавшиеся прямо в атмосфере после торможения) аэростатные зонды советских АМС Вега-1 и Вега-2. А без слова "аэродинамически" формально-верно из-за слова "планета", но всё-таки тогда стоило было бы вспомнить про Луну (откуда взлетали как Apollo, так и советские Луна-16, Луна-20, Луна-24, недавний китайский Чанъэ-5), да и с астероидов тоже были взлёты — можно вспомнить японские Хаябусу и Хаябусу-2, летящий сейчас OSIRIS-REx...
А ещё этот вертолётик несёт на себе микроскопический кусочек ткани с того самого самолёта братьев Райт; жест совершенно символический — но очень красивый.
Кадр из только что закончившейся прямой трансляции NASA : показания альтиметра (взлёт, зависание, посадка) + см. новость N+1.
Момент полёта — https://youtu.be/p1KolyCqICI?t=2524
Формулировка про "тяжелее воздуха" тут точная — в атмосфере Венеры летали (надувавшиеся прямо в атмосфере после торможения) аэростатные зонды советских АМС Вега-1 и Вега-2. А без слова "аэродинамически" формально-верно из-за слова "планета", но всё-таки тогда стоило было бы вспомнить про Луну (откуда взлетали как Apollo, так и советские Луна-16, Луна-20, Луна-24, недавний китайский Чанъэ-5), да и с астероидов тоже были взлёты — можно вспомнить японские Хаябусу и Хаябусу-2, летящий сейчас OSIRIS-REx...
А ещё этот вертолётик несёт на себе микроскопический кусочек ткани с того самого самолёта братьев Райт; жест совершенно символический — но очень красивый.
Кадр из только что закончившейся прямой трансляции NASA : показания альтиметра (взлёт, зависание, посадка) + см. новость N+1.
Момент полёта — https://youtu.be/p1KolyCqICI?t=2524
Victor Kleptsyn
М
18:15
Математические байки
Ж
Жалкие низкочастотники 19.04.2021 17:56:50
Напишу немного про проклятье размерности. Это термин, которым, в частности, называют странности многомерных пространств, от которых человеческая интуиция начинает давать сбои.
Один популярный пример выглядит так: возьмём квадрат на плоскости и впишем в него круг. Ясно, что круг закроет большую часть площади квадрата. Дальше, возьмём куб и впишем в него шар. Опять же, шар займёт большую часть объёма куба. Но вот в четырёхмерном случае гиперсфера займёт меньше трети объёма гиперкуба, а при дальнейшем повышении размерности отношение их объёмов сходится к нулю. При этом евклидово расстояние от центра n-мерного куба до любого из его
Другой пример — гипотеза Борсука о возможности разбиения n-мерного тела диаметром 1 на n+1 тел диаметром меньше 1. Она доказана для
Всё это обычно выглядит как игры разума, не отягощённого бытовыми мелочами, однако бум нейросетей принес нам популярность всяких многомерных эмбеддингов и представлений — слов, текстов или картинок, и там такие пакости случаются регулярно. Недавно, в одной из задач мне пришлось столкнуться с такой штукой:
Возьмём, скажем, 100-мерное пространство и выберем в нём равномерно случайно из единичного гиперкуба 42 точки. Пронумеруем их в некотором случайном, но фиксированном порядке, от 1 до 42. Какова вероятность, что в нашем пространстве найдётся такая ось, в проекции на которую наши точки выстроятся в нужном порядке? Ответ: больше 99%. Кому интересно, можете посмотреть мой скрипт на питоне, которым это эмпирически можно проверить (работает довольно долго, решает системы линейных неравенств, пересекая полупространства для каждой пары точек).
Один популярный пример выглядит так: возьмём квадрат на плоскости и впишем в него круг. Ясно, что круг закроет большую часть площади квадрата. Дальше, возьмём куб и впишем в него шар. Опять же, шар займёт большую часть объёма куба. Но вот в четырёхмерном случае гиперсфера займёт меньше трети объёма гиперкуба, а при дальнейшем повышении размерности отношение их объёмов сходится к нулю. При этом евклидово расстояние от центра n-мерного куба до любого из его
2^n углов растёт как sqrt(n), т.е. неограниченно; а основной объём пространства (т.е., например, основная часть равномерно случайно взятых точек) внутри такого куба оказывается на расстоянии от центра с матожиданием sqrt(n/3) и с убывающей к нулю дисперсией. Короче, n-мерный куб — это очень странное место, с кучей углов и пустым центром.Другой пример — гипотеза Борсука о возможности разбиения n-мерного тела диаметром 1 на n+1 тел диаметром меньше 1. Она доказана для
n<=3 и опровергнута для n>=64. Посредине — томящая неизвестность.Всё это обычно выглядит как игры разума, не отягощённого бытовыми мелочами, однако бум нейросетей принес нам популярность всяких многомерных эмбеддингов и представлений — слов, текстов или картинок, и там такие пакости случаются регулярно. Недавно, в одной из задач мне пришлось столкнуться с такой штукой:
Возьмём, скажем, 100-мерное пространство и выберем в нём равномерно случайно из единичного гиперкуба 42 точки. Пронумеруем их в некотором случайном, но фиксированном порядке, от 1 до 42. Какова вероятность, что в нашем пространстве найдётся такая ось, в проекции на которую наши точки выстроятся в нужном порядке? Ответ: больше 99%. Кому интересно, можете посмотреть мой скрипт на питоне, которым это эмпирически можно проверить (работает довольно долго, решает системы линейных неравенств, пересекая полупространства для каждой пары точек).
Victor Kleptsyn
М
20 April 2021
М
13:11
Математические байки
Ж
Жалкие низкочастотники 20.04.2021 12:24:45
В ответ на мой вчерашний пост в личку пришло сразу несколько бдительных математиков с разумными комментариями, которые я выношу в этот мини пост.
Конечно, число 42 я взял с потолка (ведь уже скоро день Полотенца), и вместо него могло быть другое число. И действительно, если немного подумать, то можно аналитически показать, что в n-мерном пространстве такую ось можно провести для любых n невырожденных точек (доказывается, например, построением базиса из векторов к этим точкам, а потом построением нужной оси в этом базисе).
Спасибо, Федя, Витя и все остальные, кто пишет мне уточнения и комментарии к моим постам :)
Конечно, число 42 я взял с потолка (ведь уже скоро день Полотенца), и вместо него могло быть другое число. И действительно, если немного подумать, то можно аналитически показать, что в n-мерном пространстве такую ось можно провести для любых n невырожденных точек (доказывается, например, построением базиса из векторов к этим точкам, а потом построением нужной оси в этом базисе).
Спасибо, Федя, Витя и все остальные, кто пишет мне уточнения и комментарии к моим постам :)
Victor Kleptsyn
М
13:42
Математические байки
===
Один из самых классических объектов в комбинаторике — это число разбиений p(n): сколькими способами число n можно представить в виде суммы натуральных слагаемых, если мы не различаем способы, отличающиеся только порядком слагаемых (или, что то же самое, предполагаем, что слагаемые упорядочены по неубыванию).
Так,
p(1)=1,
p(2)=2 (потому что 2=1+1),
p(3)=3 (потому что 3=2+1=1+1+1),
p(4)=5 (потому что 4=3+1=2+2=2+1+1=1+1+1+1),
p(5)=7 (упражнение),
и так далее.
Разбиению числа n можно сопоставить диаграмму Юнга: фигуру из клеток в первом квадранте, у которой число клеток в k-й строке это k-е слагаемое. Например, вот диаграмма Юнга для разбиения 15=6+5+3+1:
Один из самых классических объектов в комбинаторике — это число разбиений p(n): сколькими способами число n можно представить в виде суммы натуральных слагаемых, если мы не различаем способы, отличающиеся только порядком слагаемых (или, что то же самое, предполагаем, что слагаемые упорядочены по неубыванию).
Так,
p(1)=1,
p(2)=2 (потому что 2=1+1),
p(3)=3 (потому что 3=2+1=1+1+1),
p(4)=5 (потому что 4=3+1=2+2=2+1+1=1+1+1+1),
p(5)=7 (упражнение),
и так далее.
Разбиению числа n можно сопоставить диаграмму Юнга: фигуру из клеток в первом квадранте, у которой число клеток в k-й строке это k-е слагаемое. Например, вот диаграмма Юнга для разбиения 15=6+5+3+1:
Victor Kleptsyn
13:54
Хорошей замкнутой формулы (как формула Бине для чисел Фибоначчи) для чисел разбиения нет; интересно, что их количество растёт быстрее, чем любой полином, но медленнее, чем экспонента:
Victor Kleptsyn
13:56
Но — если замкнутой формулы нет, то как можно (при желании) вычислять p(n) при большом n? Скажем, если перебор всех
p(100)=190569292
разбиений числа n=100 ещё можно поручить компьютеру, то перебирать все
p(1000)=24061467864032622473692149727991
разбиения числа n=1000 кажется не очень продуктивной идеей.
Один "технический" способ решения этого вопроса — это находить больше. А именно, пусть p_k(n) — число разбиений n в сумму (невозрастающих) слагаемых, которые все не превосходят данного k. Тогда, с одной стороны, p(n)=p_n(n), а с другой — числа p_k(n) уже несложно ищутся рекурсивно, когда мы перебираем варианты для самого большого слагаемого:
p_k(n) = \sum_{j=1}^k p_j(n-j).
p(100)=190569292
разбиений числа n=100 ещё можно поручить компьютеру, то перебирать все
p(1000)=24061467864032622473692149727991
разбиения числа n=1000 кажется не очень продуктивной идеей.
Один "технический" способ решения этого вопроса — это находить больше. А именно, пусть p_k(n) — число разбиений n в сумму (невозрастающих) слагаемых, которые все не превосходят данного k. Тогда, с одной стороны, p(n)=p_n(n), а с другой — числа p_k(n) уже несложно ищутся рекурсивно, когда мы перебираем варианты для самого большого слагаемого:
p_k(n) = \sum_{j=1}^k p_j(n-j).
Victor Kleptsyn
М
15:15
Математические байки
Но нас будет интересовать другой способ — оказывается, на сами p(n) тоже есть рекуррентное соотношение, только чуть более сложное! Вот оно:
p(n)=p(n-1)+p(n-2)-p(n-5)-p(n-7)+p(n-12)+p(n-15)-...
(Сумма обрывается, как только аргумент у p становится отрицательным.)
p(n)=p(n-1)+p(n-2)-p(n-5)-p(n-7)+p(n-12)+p(n-15)-...
(Сумма обрывается, как только аргумент у p становится отрицательным.)
Victor Kleptsyn
21 April 2021
М
11:34
Математические байки
Применение этого равенства — кадр из великолепного видео Mathologer-а "The hardest "What comes next?" (Euler's pentagonal formula)" — которое я очень всем советую.
Victor Kleptsyn
11:36
Как это соотношение можно получить? Беглый взгляд показывает, что это явно что-то нетривиальное.
Поэтому давайте его временно отложим в сторону, и применим к последовательности p(n) стандартный молоток (а точнее, кувалду) комбинаторики — рассмотрим производящую функцию этой последовательности:
P(q):=\sum_{n=0}^{\infty} p(n) q^n.
Поэтому давайте его временно отложим в сторону, и применим к последовательности p(n) стандартный молоток (а точнее, кувалду) комбинаторики — рассмотрим производящую функцию этой последовательности:
P(q):=\sum_{n=0}^{\infty} p(n) q^n.
Victor Kleptsyn
11:39
Если бы мы работали не со всеми разбиениями n, а только с разбиениями в сумму слагаемых, не превосходящих k, то производящая функция развалилась бы в произведение k скобок-сомножителей:
Victor Kleptsyn
11:41
Первая скобка отвечает за единицы, вторая за двойки, и так далее — так что (сгруппировав одинаковые слагаемые) разбиению n, в котором a_1 единиц, a_2 двоек,..., a_k слагаемых, равных k, мы сопоставляем произведение мономов из этих скобок, где q^{1*a_1} взят из первой скобки, q^{2*a_2} из второй, и т. д..
А дальше — каждая скобка "собирается", как сумма геометрической прогрессии.
А дальше — каждая скобка "собирается", как сумма геометрической прогрессии.
Victor Kleptsyn
11:42
Если ограничения на величину слагаемых нет — получается уже просто бесконечное произведение:
Victor Kleptsyn
11:56
Теперь давайте посмотрим на обратный ряд к P(q) — просто формально записав Q(q)=1/P(q).
Victor Kleptsyn
11:57
In reply to this message
Из разложения P в произведение мы знаем и разложение Q; давайте раскроем скобки — и пусть c_n это получившиеся коэффициенты.
Victor Kleptsyn
12:00
Если действительно руками скобки пораскрывать, то вдруг (совершенно поразительно) окажется, что почти всё сократилось:
Q(q) = 1 -q -q^2 +q^5 +q^7 - q^12 - q^15 +...
Q(q) = 1 -q -q^2 +q^5 +q^7 - q^12 - q^15 +...
Victor Kleptsyn
М
12:58
Математические байки
In reply to this message
Знакомая последовательность?
И уже понятно, откуда взялась рекуррентная формула выше: это мы записали произведение P(q)*Q(q)=1 и приравняли коэффициенты при q^n в левой и в правой частях равенства: при всех n>0
\sum_{j=0}^n c_j p(n-j) = p(n)-p(n-1)-p(n-2)+p(n-5)+p(n-7)-... =0.
И уже понятно, откуда взялась рекуррентная формула выше: это мы записали произведение P(q)*Q(q)=1 и приравняли коэффициенты при q^n в левой и в правой частях равенства: при всех n>0
\sum_{j=0}^n c_j p(n-j) = p(n)-p(n-1)-p(n-2)+p(n-5)+p(n-7)-... =0.
Victor Kleptsyn
13:12
А вот статья "О раскрытии скобок, об Эйлере, Гауссе, Макдональде и об упущенных возможностях" Д. Фукса (да, того самого, который Фукс-Табачников) в Кванте, которую цитирует Ландо. И я её очень советую прочитать — даже если начало покажется простым, к концу становится ну очень интересно. На скриншоте выше один кусочек картинка оттуда — как раз из второй половины статьи.
Victor Kleptsyn
13:25
Остаётся понять, что же это за последовательность —
1, 2, 5, 7, 12, 15, 22, 26, ...
1, 2, 5, 7, 12, 15, 22, 26, ...
Victor Kleptsyn
13:26
Если посмотреть на разницу между числами пар, идущих с одинаковым знаком, то закономерность бросается в глаза:
2-1= 1
7-5= 2
15-12= 3
26-22= 4.
2-1= 1
7-5= 2
15-12= 3
26-22= 4.
Victor Kleptsyn
13:31
А как устроена последовательность первых чисел в паре?
1, 5, 12, 22...
Давайте я тут процитирую дубнинскую брошюру Е. Ю. Смирнова,
"Диаграммы Юнга, плоские разбиения и знакочередующиеся матрицы":
1, 5, 12, 22...
Давайте я тут процитирую дубнинскую брошюру Е. Ю. Смирнова,
"Диаграммы Юнга, плоские разбиения и знакочередующиеся матрицы":
Victor Kleptsyn
13:41
Вот из-за этих пятиугольных чисел соответствующее утверждение о том, как устроен ряд Q, обратный к производящей функции P, и называется пентагональной теоремой Эйлера.
Я продолжу цитировать брошюру Е. Ю. Смирнова (собственно, из неё — и из его курса в ЛШСМ — я в первый раз этот сюжет и узнал):
Я продолжу цитировать брошюру Е. Ю. Смирнова (собственно, из неё — и из его курса в ЛШСМ — я в первый раз этот сюжет и узнал):
Victor Kleptsyn
13:45
In reply to this message
Да, пока я не забыл — Mathologer в своём ролике угадывает всю последовательность через последовательные разности, раскрашивая их в два цвета. Тоже очень наглядно!
Victor Kleptsyn
М
14:35
Математические байки
In reply to this message
Итак, пентагональная теорема Эйлера сформулирована. Осталось её доказать.
Я знаю два её доказательства. Первое чуть более "лобовое": давайте раскроем все скобки в левой части — в произведении всех (1-q^j), и посмотрим, из чего складывается коэффициент при q^n. А именно — вклад получается из разложения n в сумму различных слагаемых. Причём из-за минусов перед каждым q^j разложение входит со знаком, отвечающим чётности числа слагаемых.
Поэтому в чуть-чуть изменённом виде пентагональная теорема звучит так: для всех n, кроме появляющихся в правой части тождества, число N_E(n) способов разбить n в сумму чётного числа различных слагаемых совпадает с числом N_O(n) способов разбить в сумму нечётного числа различных. А для появляющихся в правой части N_O(n) и N_E(n) отличаются на 1 (в нужную сторону).
Я знаю два её доказательства. Первое чуть более "лобовое": давайте раскроем все скобки в левой части — в произведении всех (1-q^j), и посмотрим, из чего складывается коэффициент при q^n. А именно — вклад получается из разложения n в сумму различных слагаемых. Причём из-за минусов перед каждым q^j разложение входит со знаком, отвечающим чётности числа слагаемых.
Поэтому в чуть-чуть изменённом виде пентагональная теорема звучит так: для всех n, кроме появляющихся в правой части тождества, число N_E(n) способов разбить n в сумму чётного числа различных слагаемых совпадает с числом N_O(n) способов разбить в сумму нечётного числа различных. А для появляющихся в правой части N_O(n) и N_E(n) отличаются на 1 (в нужную сторону).
Victor Kleptsyn
14:44
И очень естественная идея — если нужно доказывать, что два множества одной мощности, то можно попробовать между ними построить биекцию (а если множества отличаются на 1 по мощности — то какой-то элемент из области определения выпустить).
Именно так это доказательство и проводится — а именно, на множестве разбиений n на различные слагаемые строится инволюция (отображение, в квадрате равное тождественному), гарантированно меняющая чётность числа слагаемых. И иногда (как раз для тех самых n) определённая не на всех разбиениях, а на всех, кроме одного.
Именно так это доказательство и проводится — а именно, на множестве разбиений n на различные слагаемые строится инволюция (отображение, в квадрате равное тождественному), гарантированно меняющая чётность числа слагаемых. И иногда (как раз для тех самых n) определённая не на всех разбиениях, а на всех, кроме одного.
Victor Kleptsyn
М
15:15
Математические байки
И инволюция эта очень простая. Давайте возьмём какое-нибудь разбиение n в сумму различных слагаемых и отметим на его диаграмме Юнга как самое маленькое слагаемое, так и "последнюю диагональ":
Victor Kleptsyn
15:20
После чего, если самое маленькое слагаемое не превосходит этой диагонали — отрежем его и перенесём к диагонали, по одной клетке сверху. Скажем, из такого разбиения —
Victor Kleptsyn
15:20
получится вот такое:
Victor Kleptsyn
15:21
И обратно — если диагональ строго меньше наименьшего слагаемого, то отрежем её и перенесём эти клетки вниз, в качестве нового наименьшего слагаемого.
Victor Kleptsyn
15:23
Собственно — вот скриншот из лекции Е. Ю. Смирнова из его курса по перечислительной комбинаторике на Coursera (Image credit: Coursera + HSE + E. Smirnov)
Victor Kleptsyn
15:25
И вот так эта биекция и работает — за исключением тех случаев, когда диагональ доходит аж до самого наименьшего слагаемого, причём или равна ему по длине, или на 1 меньше: тогда её отрезать и убрать вниз не получится.
Victor Kleptsyn
15:38
А это и есть числа в правой части пентагональной теоремы: это же и есть почти совсем правильные пятиугольники, только нарисованные на квадратной решётке, так что получается квадрат + треугольник.
Victor Kleptsyn
15:38
Или так —
Victor Kleptsyn
15:39
И видно, почему между парами чисел действительно расстояния совпадают с номером пары. Давайте я покажу ещё один кадр из того же видео Mathologer-а:
Victor Kleptsyn
15:40
Image credit: Mathologer, "The hardest "What comes next?" (Euler's pentagonal formula)".
Victor Kleptsyn
23 April 2021
М
14:54
Математические байки
Коллеги напоминают про обзор Игоря Пака, «Partition bijections, а Survey» — и я присоединяюсь к рекомендации (это и вообще очень интересный обзор, и там есть эта биекция).
Victor Kleptsyn
М
М
25 April 2021
М
11:46
Математические байки
In reply to this message
Да, я не сказал — эта инволюция именная, и называется инволюцией Франклина. Вот тут — в Comptes Rendus — в 1881 году она опубликована; а вот 80-страничная статья J. J. Sylvester and F. Franklin, American Journal of Mathematics, 1882, Vol. 5, No. 1 (1882), pp. 251-330 с отдельно замечательным названием:
Victor Kleptsyn
11:50
Несколько относящихся к биекции Франклина кусочков из этой большой статьи:
Victor Kleptsyn
27 April 2021
М
11:22
Математические байки
In reply to this message
Да, ещё — к рекуррентной формуле для p(n) можно прийти и "лобовым" подходом (via). А именно, давайте опять посмотрим на более подробную информацию, но на этот раз ограничим не наибольшее слагаемое, а зафиксируем наименьшее: пусть p(n,j) это число разбиений n с наименьшим слагаемым, равным j.
Тогда:
p(n)=p(n+1,1) — потому что можно к любому разбиению дописать 1; иными словами,
p(n,1)=p(n-1).
p(n)=\sum_{j=1}^n p(n,j) — потому что последнее слагаемое должно быть хоть каким-нибудь.
А дальше можно делать индукцию "уменьшением j":
p(n,j) = p(n-1,j-1) - p(n-j,j-1),
первое — это если мы на 1 уменьшили наименьшее слагаемое j, а второе — это лишние слагаемые, которые мы при этом посчитали (предыдущее слагаемое это тоже (j-1), а не хотя бы j, так что 1 обратно к последнему добавить нельзя).
Тогда:
p(n)=p(n+1,1) — потому что можно к любому разбиению дописать 1; иными словами,
p(n,1)=p(n-1).
p(n)=\sum_{j=1}^n p(n,j) — потому что последнее слагаемое должно быть хоть каким-нибудь.
А дальше можно делать индукцию "уменьшением j":
p(n,j) = p(n-1,j-1) - p(n-j,j-1),
первое — это если мы на 1 уменьшили наименьшее слагаемое j, а второе — это лишние слагаемые, которые мы при этом посчитали (предыдущее слагаемое это тоже (j-1), а не хотя бы j, так что 1 обратно к последнему добавить нельзя).
Victor Kleptsyn
11:26
Поэтому слагаемые p(n,1), p(n,2), p(n,3),..., составляющие p(n), переписываются как
p(n,1) =p(n-1),
p(n,2)=p(n-1,1)-p(n-2,1) =p(n-2)-p(n-3),
p(n,3)=p(n-1,2)-p(n-3,2)=(p(n-2,1)-p(n-3,1))-(p(n-4,1)-p(n-5,1))
=p(n-3) - p(n-4) -p(n-5) + p(n-6),
и так далее.
p(n,1) =p(n-1),
p(n,2)=p(n-1,1)-p(n-2,1) =p(n-2)-p(n-3),
p(n,3)=p(n-1,2)-p(n-3,2)=(p(n-2,1)-p(n-3,1))-(p(n-4,1)-p(n-5,1))
=p(n-3) - p(n-4) -p(n-5) + p(n-6),
и так далее.
Victor Kleptsyn
11:33
Мы получаем сумму слагаемых вида p(n-s) со знаками. Причём, если раскрыть все скобки, то p(n-s) появляется по одному разу на способ его представить в виде суммы различных слагаемых: разница аргументов p(.,.) на каждом шаге либо сохраняется, либо уменьшается на j-1 (а на первом шаге, при сумме по j, равна n-j). При этом каждое увеличение на j-1 меняет знак.
Вот и получается, что каждое p(n-s) в итоге участвует с весом, равным числу способов представить s как сумму нечётного числа различных слагаемых минус число способов как сумму чётного их числа.
Вот и получается, что каждое p(n-s) в итоге участвует с весом, равным числу способов представить s как сумму нечётного числа различных слагаемых минус число способов как сумму чётного их числа.
Victor Kleptsyn
М
11:55
Математические байки
А ещё можно задуматься — если инволюцию Франклина придумал аж в 1881-м Франклин, то как же пентагональную теорему (больше, чем на 120 лет раньше!) доказывал сам Эйлер?
И там всё интересно! Собственно, когда я начинал эту байку записывать, я ответа не знал — спасибо Феде Петрову за рассказ и за ссылки!
И там всё интересно! Собственно, когда я начинал эту байку записывать, я ответа не знал — спасибо Феде Петрову за рассказ и за ссылки!
Victor Kleptsyn
12:09
Доказал Эйлер её, собственно, далеко не сразу. В 1740-м, заинтересовавшись этой темой после письма Филиппа Науде (Philippe Naudé) — где был, среди прочего, вопрос "сколькими способами можно представить 50 в виде суммы 7 различных слагаемых" — Эйлер её открывает экспериментально. Упоминает в том же 1740-м в письме Даниилу Бернулли, и включает в свою статью "Observationes analyticae variae de combinationibus", которую подаёт в 1741 году.
Вот тут можно посмотреть на скан, видимо, оригинального издания; вот тут — на неё в его полном собрании сочинений, тоже на латыни; а вот тут — на английский перевод. Кстати — выхода статьи ему пришлось ждать 10 лет(!):
Вот тут можно посмотреть на скан, видимо, оригинального издания; вот тут — на неё в его полном собрании сочинений, тоже на латыни; а вот тут — на английский перевод. Кстати — выхода статьи ему пришлось ждать 10 лет(!):
Victor Kleptsyn
М
16:10
Математические байки
Н
Непрерывное математическое образование 27.04.2021 15:37:16
коллеги из МКН СПбГУ сообщают, что сегодня (27.04) в 17 часов Федор Петров будет разбирать избранные задачи Всероссийской олимпиады по математике этого года
zoom ID 833 2177 9056
pass 225225
тж. обещают трансляцию на
https://www.youtube.com/channel/UCyE7AvYBGTt0uPV_WTWRvTg
zoom ID 833 2177 9056
pass 225225
тж. обещают трансляцию на
https://www.youtube.com/channel/UCyE7AvYBGTt0uPV_WTWRvTg
Victor Kleptsyn
28 April 2021
М
10:27
Математические байки
In reply to this message
Так вот, продолжая историю про Эйлера.
1747-й год, пентагональная теорема все ещё только гипотеза.
Эйлер открывает другое утверждение — на этот раз о сумме делителей.
А именно — пусть σ(n) это сумма всех делителей числа n, включая 1 и его самого. Последовательность значений σ(n) —
1, 3, 4, 7, 6, 12, 8, 15, ... .
На вид достаточно нерегулярная — что естественно, σ(n) хорошо связано с разложением n на простые множители, но у n и у n+1 разложения совершенно разные.
Так вот — Эйлер обнаруживает, что она подчиняется практически такому же рекуррентному соотношению, что и p(n), с единственной заменой: если в правой части возникает σ(0), то нужно вместо него подставить n.
Он публикует статью Découverte d'une loi tout extraordinaire des nombres par rapport à la somme de leurs diviseurs — оригинал на французском можно найти тут, а ещё она в переводе вошла в книгу Пойа "Математика и правдоподобные рассуждения", см. главу VI.
Смотрите (подстановку n вместо σ(0) я выделяю жирным) :
σ(1)=1;
σ(2)=σ(2-1)+2=3;
σ(3)=σ(3-1)+σ(3-2)=1+3=4;
σ(4)=σ(4-1)+σ(4-2)=7;
σ(5)=σ(5-1)+σ(5-2)-5=4+7-5=6;
σ(6)=σ(6-1)+σ(6-2)-σ(6-5)=7+6-1=12;
σ(7)=σ(7-1)+σ(7-2)-σ(7-5)-7=12+6-3-7=8;
...
Удивительно, правда?
1747-й год, пентагональная теорема все ещё только гипотеза.
Эйлер открывает другое утверждение — на этот раз о сумме делителей.
А именно — пусть σ(n) это сумма всех делителей числа n, включая 1 и его самого. Последовательность значений σ(n) —
1, 3, 4, 7, 6, 12, 8, 15, ... .
На вид достаточно нерегулярная — что естественно, σ(n) хорошо связано с разложением n на простые множители, но у n и у n+1 разложения совершенно разные.
Так вот — Эйлер обнаруживает, что она подчиняется практически такому же рекуррентному соотношению, что и p(n), с единственной заменой: если в правой части возникает σ(0), то нужно вместо него подставить n.
Он публикует статью Découverte d'une loi tout extraordinaire des nombres par rapport à la somme de leurs diviseurs — оригинал на французском можно найти тут, а ещё она в переводе вошла в книгу Пойа "Математика и правдоподобные рассуждения", см. главу VI.
Смотрите (подстановку n вместо σ(0) я выделяю жирным) :
σ(1)=1;
σ(2)=σ(2-1)+2=3;
σ(3)=σ(3-1)+σ(3-2)=1+3=4;
σ(4)=σ(4-1)+σ(4-2)=7;
σ(5)=σ(5-1)+σ(5-2)-5=4+7-5=6;
σ(6)=σ(6-1)+σ(6-2)-σ(6-5)=7+6-1=12;
σ(7)=σ(7-1)+σ(7-2)-σ(7-5)-7=12+6-3-7=8;
...
Удивительно, правда?
Victor Kleptsyn
М
10:50
Математические байки
Мне хочется воспроизвести тут полностью то, что Эйлер пишет в первом абзаце своей статьи:
===
До сих пор математики тщетно пытались обнаружить в последовательности простых чисел какой-либо порядок, и мы имеем все основания верить, что здесь существует какая-то тайна, в которую человеческий ум никогда не проникнет. Чтобы убедиться, следует только взглянуть на таблицу простых чисел, которую некоторые взяли на себя труд вычислить дальше чем до ста тысяч, и осознать, что здесь нет никакого порядка и никакого правила. Это тем более удивительно, что арифметика дает нам определенные правила, с помощью которых мы можем продолжать последовательность простых чисел сколь угодно далеко, не замечая, однако, ни малейшего следа порядка. Я сам, конечно, далек от этой цели, но мне удалось открыть чрезвычайно странный закон, управляющий последовательностью сумм делителей целых чисел, которая на первый взгляд кажется неправильной ровно в такой же степени, как и последовательность простых чисел, и которая в некотором смысле даже включает в себя эту последнюю. Этот закон, который я вскоре объясню, по моему мнению, тем более замечателен, что он имеет такую природу, что мы можем быть уверены в его справедливости, не давая ему безукоризненного доказательства. Тем не менее я представлю в его пользу такие доводы, которые можно рассматривать как почти равносильные строгому доказательству.
===
(цит. по: Д. Пойа, Математика и правдоподобные рассуждения, глава VI)
===
До сих пор математики тщетно пытались обнаружить в последовательности простых чисел какой-либо порядок, и мы имеем все основания верить, что здесь существует какая-то тайна, в которую человеческий ум никогда не проникнет. Чтобы убедиться, следует только взглянуть на таблицу простых чисел, которую некоторые взяли на себя труд вычислить дальше чем до ста тысяч, и осознать, что здесь нет никакого порядка и никакого правила. Это тем более удивительно, что арифметика дает нам определенные правила, с помощью которых мы можем продолжать последовательность простых чисел сколь угодно далеко, не замечая, однако, ни малейшего следа порядка. Я сам, конечно, далек от этой цели, но мне удалось открыть чрезвычайно странный закон, управляющий последовательностью сумм делителей целых чисел, которая на первый взгляд кажется неправильной ровно в такой же степени, как и последовательность простых чисел, и которая в некотором смысле даже включает в себя эту последнюю. Этот закон, который я вскоре объясню, по моему мнению, тем более замечателен, что он имеет такую природу, что мы можем быть уверены в его справедливости, не давая ему безукоризненного доказательства. Тем не менее я представлю в его пользу такие доводы, которые можно рассматривать как почти равносильные строгому доказательству.
===
(цит. по: Д. Пойа, Математика и правдоподобные рассуждения, глава VI)
Victor Kleptsyn
М
11:31
Математические байки
In reply to this message
На самом деле, когда утверждение уже есть, его вывод из пентагональной теоремы очень естественен. Я очень люблю принцип "видишь длинное произведение — прологарифмируй!"; если прологарифмировать произведение
Q(x)=(1-x)(1-x^2)(1-x^3)(1-x^4)(1-x^5)...,
стоящее с одной из сторон равенства в пентагональной теореме, то получается сумма
ln Q(x) = \sum_d ln(1-x^d).
Если её теперь продифференцировать, то логарифмы исчезают, и остаётся
Q'(x)/Q(x) = \sum_d d*x^{d-1}/(1-x^d).
И если теперь домножить на x, то в правой части получается в точности производящая функция для σ(n)!
Q(x)=(1-x)(1-x^2)(1-x^3)(1-x^4)(1-x^5)...,
стоящее с одной из сторон равенства в пентагональной теореме, то получается сумма
ln Q(x) = \sum_d ln(1-x^d).
Если её теперь продифференцировать, то логарифмы исчезают, и остаётся
Q'(x)/Q(x) = \sum_d d*x^{d-1}/(1-x^d).
И если теперь домножить на x, то в правой части получается в точности производящая функция для σ(n)!
Victor Kleptsyn
11:34
Собственно — вот, как об этом пишет сам Эйлер:
Victor Kleptsyn
11:37
И давайте для следующего шага я приведу скриншот совсем из оригинала:
Victor Kleptsyn
11:39
In reply to this message
Видно, каждая дробь dx^d/(1-x^d) как раз даёт вклад d в коэффициент при каждой степени x^n с n, делящимся на d — вот "по столбцам" и получается производящая функция для суммы делителей σ(n).
Victor Kleptsyn
М
12:05
Математические байки
Ну и остаётся совсем ничего: если Q(x) это исходное произведение, а T(x) это производящая функция для σ(n), то пентагональная теорема утверждает, что
Q(x)= 1 -x -x^2 +x^5 +x^7 - ...,
а мы только что получили, что
xQ'(x)/Q(x) = T(x).
Если домножить на знаменатель — то получается
T(x)*Q(x)=xQ'(x).
И приравнивание коэффициентов при x^n как раз и даёт то самое рекуррентное соотношение на σ(n); а появление n вместо σ(0) происходит из-за правой части (где для [обобщённых] пятиугольных n коэффициент умножается на n).
Q(x)= 1 -x -x^2 +x^5 +x^7 - ...,
а мы только что получили, что
xQ'(x)/Q(x) = T(x).
Если домножить на знаменатель — то получается
T(x)*Q(x)=xQ'(x).
И приравнивание коэффициентов при x^n как раз и даёт то самое рекуррентное соотношение на σ(n); а появление n вместо σ(0) происходит из-за правой части (где для [обобщённых] пятиугольных n коэффициент умножается на n).
Victor Kleptsyn
М
12:24
Математические байки
Но — поскольку на тот момент пентагональная теорема всё ещё не доказана, то в таком же статусе оказывается и рекуррентное соотношение: "таких совпадений не бывает", "так должно продолжаться и дальше", но формально не доказано.
Доказательство пентагональной теоремы Эйлер получит только ещё через несколько лет: в 1750-м он отправит его в письме Гольдбаху, а затем включит в статью "Demonstratio theorematis circa ordinem in summis divisorum observatum", Novi commentarii academiae scientiarum Petropolitanae 5 (1754/5), 1760, p. 75-83.
Доказательство пентагональной теоремы Эйлер получит только ещё через несколько лет: в 1750-м он отправит его в письме Гольдбаху, а затем включит в статью "Demonstratio theorematis circa ordinem in summis divisorum observatum", Novi commentarii academiae scientiarum Petropolitanae 5 (1754/5), 1760, p. 75-83.
Victor Kleptsyn
М
12:42
Математические байки
Да, я тут основываюсь на статье J. Bell, A summary of Euler's work on the pentagonal number theorem, Archive for History of Exact Sciences,
Vol. 64, No. 3 (May 2010), pp. 301-373, —
и вот абзац с хронологией оттуда.
(А вот его же препринт на arXiv-е, правда, сильно более короткий; кстати — кажется, первый раз, когда я вижу в аннотации препринта версию на латыни.)
Vol. 64, No. 3 (May 2010), pp. 301-373, —
и вот абзац с хронологией оттуда.
(А вот его же препринт на arXiv-е, правда, сильно более короткий; кстати — кажется, первый раз, когда я вижу в аннотации препринта версию на латыни.)
Victor Kleptsyn
М
13:24
Математические байки
Возвращаясь к доказательству самого Эйлера — на него можно смотреть несколькими способами. Давайте сначала посмотрим на то, как оно у Эйлера записано. Он начинает с того, что разлагает бесконечное произведение (1-x)(1-x^2)(1-x^3)... по последнему не-единичному сомножителю, вылезающему при раскрытии скобок:
Victor Kleptsyn
13:26
Получается бесконечная сумма уже конечных произведений. Дальше Эйлер забирает "в итог" первые слагаемые 1-x, выносит x^2 из оставшегося, и раскрывает скобки у (1-x), на который они все делятся:
Victor Kleptsyn
13:39
И тут уже понятно, как нужно формулировать утверждения (где там степени образуют арифметическую прогрессию с какой разностью) — и что как только последовательность утверждений правильно записать, мгновенно получится доказательство по индукции.
Victor Kleptsyn
13:50
Второй способ (чуть более современный взгляд) — я его увидел в статье G. Andrews, Euler's pentagonal number theorem, Mathematics Magazine 56 (1983), no. 5, 279-284 — состоит в том, чтобы рассмотреть такие суммы произведений, зависящие от двух переменных.
Victor Kleptsyn
13:52
Тогда вынесение первых двух слагаемых и раскрытие первой скобки это функциональное уравнение:
Victor Kleptsyn
13:52
(G. Andrews, Euler's pentagonal number theorem, Mathematics Magazine, vol. 56, 1983)
Victor Kleptsyn
13:53
In reply to this message
И ход доказательства Эйлера — это итеративное применение этого тождества.
Victor Kleptsyn
14:01
Но третий, совершенно прекрасный, вероятностный взгляд на всё то же доказательство придумал Федя Петров. Он описан у него вот тут, но я всё-таки пару слов скажу.
Victor Kleptsyn
14:14
Вот пусть у нас есть квадратики, в каждом из которых независимо может вырасти ёлка с вероятностью (1-x) (и, соответственно, он остаётся пустым с вероятностью x).
Тогда в прямоугольнике 1xn не вырастает ни одной ёлки с вероятностью x^n — соответственно, хоть одна вырастает с вероятностью (1-x^n).
А произведение s=(1-x)(1-x^2)(1-x^3)... — это вероятность того, что ни один из прямоугольников размера 1x1, 1x2, 1x3,... не останется пустым!
Тогда в прямоугольнике 1xn не вырастает ни одной ёлки с вероятностью x^n — соответственно, хоть одна вырастает с вероятностью (1-x^n).
А произведение s=(1-x)(1-x^2)(1-x^3)... — это вероятность того, что ни один из прямоугольников размера 1x1, 1x2, 1x3,... не останется пустым!
Victor Kleptsyn
14:17
Если смотреть на 1-s — то оно разбивается по тому, какой самый левый прямоугольник остался пустым. Либо это левая клетка (вклад x), либо пустых клеток хотя бы две (выносим x^2), а во всех прямоугольниках левее того есть хотя бы по одной ёлке (иначе бы это был не самый левый), и мы получаем бесконечную сумму конечных произведений конфигураций "вот тут ёлок нет, а вот в каждом из этих прямоугольников хотя бы одна есть".
Victor Kleptsyn
14:17
И так продолжается и дальше (image credit: F. Petrov, Euler’s proof of pentagonal theorem).
Victor Kleptsyn
14:17
По-моему, очень красиво!
Victor Kleptsyn
М
15:19
Математические байки
Текущая версия-препринт текста Феди Петрова (спасибо ему за разрешение выложить!)
Victor Kleptsyn
15:25
In reply to this message
И в этом тексте больше, чем в посте по ссылке выше — вот одна страница оттуда в качестве рекламы.
Victor Kleptsyn
29 April 2021
М
12:10
Математические байки
In reply to this message
Третий способ доказывать пентагональную теорему (и первый, который я узнал) — через тройное произведение Якоби.
Вот его формулировка из уже упоминавшейся брошюры Е. Ю. Смирнова:
Вот его формулировка из уже упоминавшейся брошюры Е. Ю. Смирнова:
Victor Kleptsyn
12:15
In reply to this message
На вид выглядит несколько пугающе: ряды уже от двух формальных переменных, q и x, причём для x бывают ещё и отрицательные степени, и в левой части стоит произведение аж трёх разных скобок. Но на самом деле — совершенно не страшно (и мы с ней скоро разберёмся). И действительно сразу проглядывает похожесть на пентагональную теорему: в левой части произведения по всем j с q^j внутри сомножителей, в правой сумма, правда, с треугольными, а не с пятиугольными показателями степеней.
Victor Kleptsyn
12:20
И пентагональная теорема из неё действительно выводится очень несложно: если подставить q^3 вместо q и -q^{-1} вместо x, то три скобки в левой части станут в точности произведением (1-q^j) из пентагональной теоремы — просто разбитым по тому, какой остаток степень j даёт при делении на 3. Если j=3k, то (1-q^j) получается из последней скобки, если j=3k-1, то из первой, а если j=3k-2, то из второй.
Ну а в правой части подстановка как раз и даёт обобщённые пятиугольные числа (со знаком, приходящим из x^j=(-q^{-1})^j) — в точности правую часть пентагональной теоремы.
Ну а в правой части подстановка как раз и даёт обобщённые пятиугольные числа (со знаком, приходящим из x^j=(-q^{-1})^j) — в точности правую часть пентагональной теоремы.
Victor Kleptsyn
12:22
(Image credit: Е. Ю. Смирнов, Диаграммы Юнга, плоские разбиения и знакочередующиеся матрицы)
Victor Kleptsyn
12:30
А вот кадр из его же курса лекций в НМУ. Мы теперь узнаём почти всё, что написано на доске (а это всегда очень приятно!).
Victor Kleptsyn
М
14:37
Математические байки
In reply to this message
Но это мы пентагональную теорему вывели из тройного произведения. А как его доказывать?
Сначала — давайте его переформулируем эквивалентным образом: произведение (1-q^k), третья скобка, это обратный ряд к производящей функции для числа разбиений p(n). Соответственно — если мы это произведение перенесём в правую часть — как раз получится производящая функция для p(n):
Сначала — давайте его переформулируем эквивалентным образом: произведение (1-q^k), третья скобка, это обратный ряд к производящей функции для числа разбиений p(n). Соответственно — если мы это произведение перенесём в правую часть — как раз получится производящая функция для p(n):
Victor Kleptsyn
14:41
In reply to this message
И вот в этом виде мы его и будем доказывать. Кстати — если обозначить левую часть через A(x,q), так это определение это в точности формула наверху центральной доски на фото выше.
Victor Kleptsyn
М
15:04
Математические байки
Да — прежде, чем мы перейдём к доказательству, давайте я скажу пару слов о способах рисовать диаграмму Юнга. Мы уже прямо в этом рассказе видели, что строчки из квадратиков, соответствующие убывающим слагаемым, можно рисовать одну под другой (см.), а можно ставить одну на другую снизу вверх (см.). Первый способ называется английским, второй французским.
Victor Kleptsyn
15:07
Естественно, не могло обойтись без юмора. На скриншоте — сноска на странице 2 книги Ian G. Macdonald-а "Symmetric Functions and Hall Polynomials":
"Some authors (especially Francophones) prefer the convention of coordinate geometry (in which the first coordinate increases from left to right and the second coordinate from bottom to top) and define the diagram of λ to be the set of (i,j) \in Z^2 such that 1 \le i \le λ_j. Readers who prefer this convention should read this book upside down in a mirror."
"Some authors (especially Francophones) prefer the convention of coordinate geometry (in which the first coordinate increases from left to right and the second coordinate from bottom to top) and define the diagram of λ to be the set of (i,j) \in Z^2 such that 1 \le i \le λ_j. Readers who prefer this convention should read this book upside down in a mirror."
Victor Kleptsyn
15:18
Victor Kleptsyn
М
16:05
Математические байки
Третий способ рисовать диаграммы Юнга называется русским: это французский способ, повёрнутый на 45 градусов в положительном направлении и растянутый в корень из 2 раз — так, что диаграмма оказывается состоящей из квадратов с вершинами с целыми координатами, а каждый отрезок её внешней границы имеет наклон плюс или минус 1.
На скриншоте — иллюстрация из статьи Дэна Ромика (Dan Romik) и Петра Сняды (Piotr Sniady), Jeu de taquin dynamics on infinite Young tableaux and second class particles, Ann. Probab. 43:2 (2015), pp. 682-737.
На скриншоте — иллюстрация из статьи Дэна Ромика (Dan Romik) и Петра Сняды (Piotr Sniady), Jeu de taquin dynamics on infinite Young tableaux and second class particles, Ann. Probab. 43:2 (2015), pp. 682-737.
Victor Kleptsyn
М
17:29
Математические байки
In reply to this message
Этот способ, хоть сначала и кажется странным (зачем на 45 градусов поворачивать, рисовать же неудобно!), оказывается очень полезным. А именно — можно продолжить внешнюю границу диаграммы графиком y=|x| (как на рисунке у Ромика-Сняды и сделано). И получить график непрерывной кусочно-линейной функции на всей прямой.
А этот график можно задавать плюсами и минусами — в зависимости от того, её наклон на очередном отрезке [n,n+1] равен +1 или -1. Или — поместить по чёрному камушку в середину каждого отрезка графика, идущего с коэффициентом наклона -1, и по белому — с коэффициентом наклона +1, а потом спроецировать эту конфигурацию на ось абсцисс и получить расстановку чёрных и белых камушков на прямой.
Можно, кстати, белые камушки не ставить, а считать, что во всех полуцелых точках прямой выкопаны лунки — только некоторые из них заняты камнями, а некоторые нет.
А этот график можно задавать плюсами и минусами — в зависимости от того, её наклон на очередном отрезке [n,n+1] равен +1 или -1. Или — поместить по чёрному камушку в середину каждого отрезка графика, идущего с коэффициентом наклона -1, и по белому — с коэффициентом наклона +1, а потом спроецировать эту конфигурацию на ось абсцисс и получить расстановку чёрных и белых камушков на прямой.
Можно, кстати, белые камушки не ставить, а считать, что во всех полуцелых точках прямой выкопаны лунки — только некоторые из них заняты камнями, а некоторые нет.
Victor Kleptsyn
17:32
Да, для того, чтобы мы восстановили диаграмму, "вписанную" в график y=|x|, нужно, чтобы:
*) в минус бесконечности, начиная с некоторого момента все лунки были бы заняты;
*) в плюс бесконечности, начиная с некоторого момента все лунки были бы свободны;
*) число свободных лунок левее нуля совпадало бы с числом занятых лунок правее нуля.
Если последнее не выполнено, то при попытке восстановить мы получим диаграмму, у которой смещено "начало" — вписанную в какой-то другой угол y=|x-k|, где k целое (это разность занятых левее нуля и свободных правее нуля).
Получающаяся расстановка называется диаграммой майя для данной диаграммы Юнга; её замечательное свойство в том, что добавление одной клетки к диаграмме Юнга это в точности перемещение одного камня на один шаг вперёд.
Вот один такой пример (рисунок из препринта A. Gordenko, Limit shapes of large skew Young tableaux and a modification of the TASEP process).
*) в минус бесконечности, начиная с некоторого момента все лунки были бы заняты;
*) в плюс бесконечности, начиная с некоторого момента все лунки были бы свободны;
*) число свободных лунок левее нуля совпадало бы с числом занятых лунок правее нуля.
Если последнее не выполнено, то при попытке восстановить мы получим диаграмму, у которой смещено "начало" — вписанную в какой-то другой угол y=|x-k|, где k целое (это разность занятых левее нуля и свободных правее нуля).
Получающаяся расстановка называется диаграммой майя для данной диаграммы Юнга; её замечательное свойство в том, что добавление одной клетки к диаграмме Юнга это в точности перемещение одного камня на один шаг вперёд.
Вот один такой пример (рисунок из препринта A. Gordenko, Limit shapes of large skew Young tableaux and a modification of the TASEP process).
Victor Kleptsyn
2 May 2021
М
16:38
Математические байки
===
Давайте я сделаю небольшую паузу — хотя история про пентагональную теорему не закончена! — и поделюсь замечательным видео, которое выложили организаторы ICM-2022 как анонс их конкурса.
Группа SL(2,Z) действует на верхней полуплоскости дробно-линейными преобразованиями — матрица (a, b \\ c, d) действует преобразованием
z-> (az+b)/(cz+d);
при этом минус тождественная матрица действует тоже тождественно, поэтому на самом деле действует группа
PSL(2,Z)=SL(2,Z)/{Id, -Id}.
Фактор верхней полуплоскости по её действию это модулярная кривая, на которой есть две конические особенности (i и e^{πi/3}, "отвечающие" квадратной и треугольной решёткам, если думать об этом действии в терминах решёток на плоскости) и один касп = "проколотая точка", отвечающий направлению "вверх на бесконечность" (или, что то же самое, вырождению решётки).
У этого действия есть стандартная фундаментальная область (склейкой границ которой модулярная кривая и получается) — вот так она выглядит в верхней полуплоскости.
Давайте я сделаю небольшую паузу — хотя история про пентагональную теорему не закончена! — и поделюсь замечательным видео, которое выложили организаторы ICM-2022 как анонс их конкурса.
Группа SL(2,Z) действует на верхней полуплоскости дробно-линейными преобразованиями — матрица (a, b \\ c, d) действует преобразованием
z-> (az+b)/(cz+d);
при этом минус тождественная матрица действует тоже тождественно, поэтому на самом деле действует группа
PSL(2,Z)=SL(2,Z)/{Id, -Id}.
Фактор верхней полуплоскости по её действию это модулярная кривая, на которой есть две конические особенности (i и e^{πi/3}, "отвечающие" квадратной и треугольной решёткам, если думать об этом действии в терминах решёток на плоскости) и один касп = "проколотая точка", отвечающий направлению "вверх на бесконечность" (или, что то же самое, вырождению решётки).
У этого действия есть стандартная фундаментальная область (склейкой границ которой модулярная кривая и получается) — вот так она выглядит в верхней полуплоскости.
Victor Kleptsyn
16:39
Но верхняя полуплоскость переводится в единичный диск дробно-линейным преобразованием
z -> (z-i)/(z+i)
(переводящим вещественную прямую в единичную окружность), так что PSL(2,Z) действует и на единичном диске, и можно рисовать фундаментальную область и там. И вот она, на первых кадрах ролика. (Кстати, дуга единичной окружности при таком преобразовании действительно переходит в вертикальный отрезок!)
(Image credit: ICM 2022)
z -> (z-i)/(z+i)
(переводящим вещественную прямую в единичную окружность), так что PSL(2,Z) действует и на единичном диске, и можно рисовать фундаментальную область и там. И вот она, на первых кадрах ролика. (Кстати, дуга единичной окружности при таком преобразовании действительно переходит в вертикальный отрезок!)
(Image credit: ICM 2022)
Victor Kleptsyn
16:42
Рассмотрим теперь подгруппу Г(5), состоящую из матриц, сравнимых с плюс или минус тождественной по модулю 5. Иными словами — ядро (сюръективного) отображения "приведения по модулю 5"
PSL(2,Z) -> PSL(2, Z/5Z).
Эта подгруппа имеет индекс, равный порядку PSL(2,Z/5Z); каковой, в свою очередь, равен
(5^2-1)*5/2=24*5/2 = 12*5=60:
если мы строим матрицу из SL(2,Z/5Z), то первый столбец может быть любым ненулевым вектором из (Z/5Z)^2, поэтому там 24 варианта, а у второго всегда ровно 5, чтобы определитель был единичным. Ну и пополам, потому что факторизуем по плюс-минус единице.
Объединив соответствующие образы фундаментальной области (по одному на класс смежности), можно получить фундаментальную область для действия Г(5).
PSL(2,Z) -> PSL(2, Z/5Z).
Эта подгруппа имеет индекс, равный порядку PSL(2,Z/5Z); каковой, в свою очередь, равен
(5^2-1)*5/2=24*5/2 = 12*5=60:
если мы строим матрицу из SL(2,Z/5Z), то первый столбец может быть любым ненулевым вектором из (Z/5Z)^2, поэтому там 24 варианта, а у второго всегда ровно 5, чтобы определитель был единичным. Ну и пополам, потому что факторизуем по плюс-минус единице.
Объединив соответствующие образы фундаментальной области (по одному на класс смежности), можно получить фундаментальную область для действия Г(5).
Victor Kleptsyn
16:47
Если фактор полуплоскости по действию PSL(2,Z) был сферой с одним каспом (и двумя коническими особенностями) — то фактор по действию Г(5) оказывается сферой с 12 каспами.
Раньше, при факторизации по PSL(2,Z), у нас была точка "на бесконечности i∞", с координатой q=exp(2πi z) в её окрестности (сдвиг z на 1 значения q не меняет, чем больше мнимая часть z, тем меньше модуль q, но нулём он никогда не будет — так что там фактор устроен, как проколотая окрестность нуля).
Теперь в группе Г(5) нет отображения z->z+1, зато есть отображение z->z+5. Поэтому в один из таких каспов собирается идущая "на i∞" полоса шириной 5 (с помощью отображения z-> q=exp(2πi z/5) ).
А жорданова клетка
(1 1)
(0 1),
соответствующая преобразованию z->z+1, этот касп оставляет на месте, поворачивая q на (1/5) оборота — и порождённая ей подгруппа порядка 5 это и есть стабилизатор этого каспа.
Раньше, при факторизации по PSL(2,Z), у нас была точка "на бесконечности i∞", с координатой q=exp(2πi z) в её окрестности (сдвиг z на 1 значения q не меняет, чем больше мнимая часть z, тем меньше модуль q, но нулём он никогда не будет — так что там фактор устроен, как проколотая окрестность нуля).
Теперь в группе Г(5) нет отображения z->z+1, зато есть отображение z->z+5. Поэтому в один из таких каспов собирается идущая "на i∞" полоса шириной 5 (с помощью отображения z-> q=exp(2πi z/5) ).
А жорданова клетка
(1 1)
(0 1),
соответствующая преобразованию z->z+1, этот касп оставляет на месте, поворачивая q на (1/5) оборота — и порождённая ей подгруппа порядка 5 это и есть стабилизатор этого каспа.
Victor Kleptsyn
16:49
И теперь на сфере-факторе появляется замечательная картина: 12 точек-каспов, окружённых пятиугольниками, которые факторгруппа
PSL(2,Z)/Г(5)=PSL(2,Z/5Z)
умеет поворачивать и переставлять друг в друга. Конечно, это вершины икосаэдра — а пятиугольники, их содержащие, образуют двойственный додекаэр!
В частности — группа PSL(2,Z/5Z) это группа движений додекаэдра, то есть A_5 !
Image credit: ICM 2022
PSL(2,Z)/Г(5)=PSL(2,Z/5Z)
умеет поворачивать и переставлять друг в друга. Конечно, это вершины икосаэдра — а пятиугольники, их содержащие, образуют двойственный додекаэр!
В частности — группа PSL(2,Z/5Z) это группа движений додекаэдра, то есть A_5 !
Image credit: ICM 2022
Victor Kleptsyn
16:50
По-моему, очень красиво!
Victor Kleptsyn
3 May 2021
М
08:27
Математические байки
Н
Непрерывное математическое образование 03.05.2021 08:25:33
https://arxiv.org/abs/1010.3465
(G.Blekherman. Nonnegative Polynomials and Sums of Squares)
«It is a central question in real algebraic geometry, whether a non-negative polynomial can be written in a way that makes its nonnegativity apparent, i.e. as a sum of squares of polynomials (or more general objects). Algorithms to obtain such representations, when they are known, have many applications in polynomial optimization [9],[10],[11].
The investigation of the relation between nonnegativity and sums of squares began in the seminal paper of Hilbert from 1888. Hilbert showed that every nonnegative polynomial is a sum of squares of polynomials only in the following 3 cases: univariate polynomials, quadratic polynomials and bivariate polynomials of degree 4. In all other cases Hilbert showed existence of nonnegative polynomials that are not sums of squares. Hilbert’s proof used the fact that polynomials of degree d satisfy linear relations, known as the Cayley-Bacharach relations, which are not satisfied by polynomials of full degree 2d [14],[15].
Hilbert then showed that every bivariate nonnegative polynomial is a sum of squares of rational functions and Hilbert’s 17th problem asked whether this is true in general. In 1920’a Artin and Schreier solved Hilbert’s 17th problem in the affirmative. However, there is no known algorithm to obtain this representation. In particular we may need to use numerators and denominators of very large degree, thus representing a simple object (the polynomial) as a sum of squares of significantly more complex objects [3].
It should be noted that Hilbert did not provide an explicit nonnegative polynomial that is not a sum of squares of polynomials, he only proved its existence. The first explicit example appeared only eighty years later and is due to Motzkin. Since then many explicit examples of nonnegative polynomials that are not sums of squares have appeared [14].»
(G.Blekherman. Nonnegative Polynomials and Sums of Squares)
«It is a central question in real algebraic geometry, whether a non-negative polynomial can be written in a way that makes its nonnegativity apparent, i.e. as a sum of squares of polynomials (or more general objects). Algorithms to obtain such representations, when they are known, have many applications in polynomial optimization [9],[10],[11].
The investigation of the relation between nonnegativity and sums of squares began in the seminal paper of Hilbert from 1888. Hilbert showed that every nonnegative polynomial is a sum of squares of polynomials only in the following 3 cases: univariate polynomials, quadratic polynomials and bivariate polynomials of degree 4. In all other cases Hilbert showed existence of nonnegative polynomials that are not sums of squares. Hilbert’s proof used the fact that polynomials of degree d satisfy linear relations, known as the Cayley-Bacharach relations, which are not satisfied by polynomials of full degree 2d [14],[15].
Hilbert then showed that every bivariate nonnegative polynomial is a sum of squares of rational functions and Hilbert’s 17th problem asked whether this is true in general. In 1920’a Artin and Schreier solved Hilbert’s 17th problem in the affirmative. However, there is no known algorithm to obtain this representation. In particular we may need to use numerators and denominators of very large degree, thus representing a simple object (the polynomial) as a sum of squares of significantly more complex objects [3].
It should be noted that Hilbert did not provide an explicit nonnegative polynomial that is not a sum of squares of polynomials, he only proved its existence. The first explicit example appeared only eighty years later and is due to Motzkin. Since then many explicit examples of nonnegative polynomials that are not sums of squares have appeared [14].»
Victor Kleptsyn
М
08:31
Математические байки
Н
Непрерывное математическое образование 03.05.2021 08:30:48
и вот еще такой текст
https://www.math.ens.fr/~benoist/articles/CarresEMS.pdf
(Oliver Benoist. Writing Positive Polynomials as Sums of (Few) Squares)
«In 1927, Artin proved that a real polynomial that is positive semidefinite is a sum of squares of rational functions, thus solving Hilbert’s 17th problem. We review Artin’s Theorem and its posterity, browsing through basic examples, classical results and recent developments. We focus on a question first considered by Pfister: can one write a positive semidefinite polynomial as a sum of few squares?
https://www.math.ens.fr/~benoist/articles/CarresEMS.pdf
(Oliver Benoist. Writing Positive Polynomials as Sums of (Few) Squares)
«In 1927, Artin proved that a real polynomial that is positive semidefinite is a sum of squares of rational functions, thus solving Hilbert’s 17th problem. We review Artin’s Theorem and its posterity, browsing through basic examples, classical results and recent developments. We focus on a question first considered by Pfister: can one write a positive semidefinite polynomial as a sum of few squares?
Victor Kleptsyn
4 May 2021
М
15:58
Математические байки
t
tropical saint petersburg 02.05.2021 13:11:01
16 мая 2021 года — 200 лет Чебышеву (произносится ЧебышЁв, пишется — Чебышев)
Самая крутая лекция (Этьена Жиса, по английски, тут по французски, см. также sine Gordon) про Чебышёва, геометрию, поверхности, как сшить форму для сферического солдата (а что человек имеет форму шара [по воскресении], то было анафематствовано поместным собором в Константинополе в 543 году в числе заблуждений оригенистов).
и лекция Коли Андреева о механизмах Чебышева
Самая крутая лекция (Этьена Жиса, по английски, тут по французски, см. также sine Gordon) про Чебышёва, геометрию, поверхности, как сшить форму для сферического солдата (а что человек имеет форму шара [по воскресении], то было анафематствовано поместным собором в Константинополе в 543 году в числе заблуждений оригенистов).
и лекция Коли Андреева о механизмах Чебышева
Victor Kleptsyn
М
15:58
Математические байки
М
Математические этюды 04.05.2021 15:17:04
4 мая по старому стилю в 1821 году родился великий российский математик Пафнутий Львович Чебышев. Сегодня, 4 мая 2021 года запущена новая современная версия интернет-музея «Механизмы П.Л. Чебышева» https://tcheb.ru/. Обновление проекта приурочено к 200-летнему юбилею великого математика, который будет отмечаться в день его рождения по новому стилю – 16 мая и в последующие дни.
Академик Императорской Санкт-Петербургской академии наук, основатель Санкт-Петербургской математической школы доказал фундаментальные результаты во многих областях математики. Это и теория чисел, и теория вероятности, и теория функций. Совмещение результатов по теории приближения функций, основоположником которой общепризнано является Чебышев, и метрическому синтезу механизмов привело к созданию более 30 интересных механизмов Они выставлялись на всемирных выставках, некоторые до сих пор хранятся в Политехническом музее г. Москвы, в музеях Санкт-Петербурга, Парижа и Лондона.
В годы Великой отечественной войны к исследованию механизмов и теорем Чебышева по метрическому синтезу механизмов академика И.И. Артоболевского подтолкнули практические задачи. Это была «вторая жизнь» механизмов. А «третья жизнь» началась уже в XXI веке, с появления фильма о движении «Стопоходящей машины», созданной Чебышевым. В 2007 году в первые «премьерные дни» его посмотрели более 100 тысяч человек и сейчас уже на ютубе можно встретить много моделей, сделанных школьниками. С этого фильма и начался проект «Механизмы П.Л. Чебышёва».
В проекте реконструированы все механизмы, созданные великим математиком. Среди них — первая в мире шагающая машина («стопоходящая»), «сортировалка», «самокатное кресло», «гребной» механизм и многие другие изобретения. Были тщательно измерены все параметры оригиналов и точно реконструированы механизмы, хранящиеся в музеях. Утраченные предметы восстанавливались по архивным документам. В фильмах проекта демонстрируется как принцип действия механизмов, так и их математическая основа – приближение заданной линии (отрезок, дуга окружности, полная окружность и др.) шатунной кривой.
Новая версия проекта стала более современной: обновлена и основанная, и мобильная версии. Все фильмы теперь представлены в 4K-разрешении. Дополнена и ещё будет дополняться информация, появившаяся уже после создания первой версии.
Академик Императорской Санкт-Петербургской академии наук, основатель Санкт-Петербургской математической школы доказал фундаментальные результаты во многих областях математики. Это и теория чисел, и теория вероятности, и теория функций. Совмещение результатов по теории приближения функций, основоположником которой общепризнано является Чебышев, и метрическому синтезу механизмов привело к созданию более 30 интересных механизмов Они выставлялись на всемирных выставках, некоторые до сих пор хранятся в Политехническом музее г. Москвы, в музеях Санкт-Петербурга, Парижа и Лондона.
В годы Великой отечественной войны к исследованию механизмов и теорем Чебышева по метрическому синтезу механизмов академика И.И. Артоболевского подтолкнули практические задачи. Это была «вторая жизнь» механизмов. А «третья жизнь» началась уже в XXI веке, с появления фильма о движении «Стопоходящей машины», созданной Чебышевым. В 2007 году в первые «премьерные дни» его посмотрели более 100 тысяч человек и сейчас уже на ютубе можно встретить много моделей, сделанных школьниками. С этого фильма и начался проект «Механизмы П.Л. Чебышёва».
В проекте реконструированы все механизмы, созданные великим математиком. Среди них — первая в мире шагающая машина («стопоходящая»), «сортировалка», «самокатное кресло», «гребной» механизм и многие другие изобретения. Были тщательно измерены все параметры оригиналов и точно реконструированы механизмы, хранящиеся в музеях. Утраченные предметы восстанавливались по архивным документам. В фильмах проекта демонстрируется как принцип действия механизмов, так и их математическая основа – приближение заданной линии (отрезок, дуга окружности, полная окружность и др.) шатунной кривой.
Новая версия проекта стала более современной: обновлена и основанная, и мобильная версии. Все фильмы теперь представлены в 4K-разрешении. Дополнена и ещё будет дополняться информация, появившаяся уже после создания первой версии.
Victor Kleptsyn
М
16:05
Математические байки
In reply to this message
Давайте продолжим про тройное произведение?
У его доказательства, которое мы сейчас проведём, есть физическая мотивация, которая сама по себе интересна. Но прежде, чем её рассказывать, я хочу предупредить, что уровень аккуратности моего рассказа этой физической части — рыбацкая байка. А, как известно, рыбацким рассказам о том, как в озере Глубоком у деревни Новодарьино попался воот такенный сомище — стоит верить в том, что озеро Глубокое и впрямь существует. Ну, если рассказчик и впрямь заслуживающий доверия — ещё что рыба в том озере есть. Хоть какая-то.
И для этой физической части мы вернёмся чуть меньше, чем на сотню лет назад. Уже написано уравнение Шрёдингера — но оно не дружит с теорией относительности. А ещё в поле притяжения точечного заряда (читай, атома) оно без доработки напильником предсказывает в два раза меньше состояний электронов, чем надо бы: тот самый спин, стрелочки вверх и вниз, которые на уроках химии рисуют в клеточках, приходится "вручную" добавлять отдельно. (Или "двухместность" комнат в статье "Дом для электронов" Валерии Сироты в "Квантике" — снимаю шляпу и пользуюсь случаем порекламировать, ибо рассказ совершенно замечательный.)
И Поль Дирак в 1928-м выводит "дружащее с преобразованиями Лоренца" уравнение, уравнение Дирака.
У его доказательства, которое мы сейчас проведём, есть физическая мотивация, которая сама по себе интересна. Но прежде, чем её рассказывать, я хочу предупредить, что уровень аккуратности моего рассказа этой физической части — рыбацкая байка. А, как известно, рыбацким рассказам о том, как в озере Глубоком у деревни Новодарьино попался воот такенный сомище — стоит верить в том, что озеро Глубокое и впрямь существует. Ну, если рассказчик и впрямь заслуживающий доверия — ещё что рыба в том озере есть. Хоть какая-то.
И для этой физической части мы вернёмся чуть меньше, чем на сотню лет назад. Уже написано уравнение Шрёдингера — но оно не дружит с теорией относительности. А ещё в поле притяжения точечного заряда (читай, атома) оно без доработки напильником предсказывает в два раза меньше состояний электронов, чем надо бы: тот самый спин, стрелочки вверх и вниз, которые на уроках химии рисуют в клеточках, приходится "вручную" добавлять отдельно. (Или "двухместность" комнат в статье "Дом для электронов" Валерии Сироты в "Квантике" — снимаю шляпу и пользуюсь случаем порекламировать, ибо рассказ совершенно замечательный.)
И Поль Дирак в 1928-м выводит "дружащее с преобразованиями Лоренца" уравнение, уравнение Дирака.
Victor Kleptsyn
16:14
Первые полтора абзаца статьи Дирака "The Quantum Theory of the Electron" (Proceedings of the Royal Society of London. Series A, vol. 117, issue 778, 01 February 1928).
(Кстати — интересно, насколько легко текст читается!)
(Кстати — интересно, насколько легко текст читается!)
Victor Kleptsyn
16:19
Сейчас неважно, как именно оно устроено — а важно то, что у него оказался, на первый взгляд, большой дефект: даже просто в вакууме в дополнение к куче [обобщённых] состояний со сколь угодно большой положительной энергией (что логично — кинетическая энергия может быть сколь угодно большой, берём да разгоняем) у него оказывались состояния с такой же, но отрицательной энергией.
А это уже создавало проблему: точно так же, как электрон у атома из возбуждённого состояния "проваливается" обратно, излучая фотон — так вот, точно так же электрон мог и должен был бы проваливаться всё глубже и глубже в эти отрицательные состояния. А этого мы не видим.
А это уже создавало проблему: точно так же, как электрон у атома из возбуждённого состояния "проваливается" обратно, излучая фотон — так вот, точно так же электрон мог и должен был бы проваливаться всё глубже и глубже в эти отрицательные состояния. А этого мы не видим.
Victor Kleptsyn
16:24
Ещё один абзац из статьи Дирака, на этот раз, присланной 6 декабря 1929 года и вышедшей 1 января 1930 года —
Dirac Paul Adrien Maurice, Theory of electrons and protons, Proc. R. Soc. Lond. A, 126, pp. 360--365.
Dirac Paul Adrien Maurice, Theory of electrons and protons, Proc. R. Soc. Lond. A, 126, pp. 360--365.
Victor Kleptsyn
16:34
Да, про излучение фотонов перепрыгивающими на более низкую орбиталь возбуждёнными электронами — мне хочется вспомнить вот эту серию из "Нобелевского сезона" "Смешариков" про фейерверки и цвет пламени; да, конечно, электроны "на орбитах" это ещё не квантовая механика, но для детей очень приятно сделано!
Victor Kleptsyn
16:35
Вообще, самое известное тут это что медь окрашивает пламя в зелёный цвет; а вот тут Маску задают вопрос про кадр из полёта SN10, "чем вызвана зелёная вспышка" и получают ответ
"Зелёное пламя в этом контексте означает, что двигатель сжигает внутренние компоненты, сделанные из меди. Обычно за этим следует Быстрая Незапланированная Разборка."
"Зелёное пламя в этом контексте означает, что двигатель сжигает внутренние компоненты, сделанные из меди. Обычно за этим следует Быстрая Незапланированная Разборка."
Victor Kleptsyn
16:41
In reply to this message
И Дирак очень красиво решил эту проблему, предложив концепцию "моря Дирака" — сказав, что да, все эти состояния тоже есть. Но они все уже заняты! И заняты они везде и всюду, и это ["нейтральное"] состояние мы воспринимаем как вакуум.
И тогда, раз все состояния с отрицательной энергией уже заняты — проблема проваливания туда снимается. Но что, если мы из одного из этих состояний электрон "достанем"?
Опять-таки, давайте я продолжу цитатой из статьи Дирака:
И тогда, раз все состояния с отрицательной энергией уже заняты — проблема проваливания туда снимается. Но что, если мы из одного из этих состояний электрон "достанем"?
Опять-таки, давайте я продолжу цитатой из статьи Дирака:
Victor Kleptsyn
16:42
In reply to this message
Dirac Paul Adrien Maurice, Theory of electrons and protons, Proc. R. Soc. Lond. A, 126, 01 January 1930, pp. 360--365.
Victor Kleptsyn
16:53
In reply to this message
Так вот, что будет, если убрать один из этого моря электронов с отрицательной энергией (выглядящего для нас, как нейтральный вакуум)? От него останется "дырка" — которая будет для нас выглядеть, как положительно заряженная частица.
А вот если электрон к такой дырке подлетит — то вот тут он с большой радостью её займёт, перепрыгнув из своего состояния с большой положительной энергией в свободное состояние с большой отрицательной, и отдав разность энергий в качестве излучения (кто сказал "аннигиляция"?).
И опять же — см. середину уже процитированного абзаца статьи Дирака:
"... transitions can take place in which the energy of the electron changes from a positive to a negative value ..., the surplus energy, at least 2mc^2 in amount, being spontaneously emitted in form of radiation."
А вот если электрон к такой дырке подлетит — то вот тут он с большой радостью её займёт, перепрыгнув из своего состояния с большой положительной энергией в свободное состояние с большой отрицательной, и отдав разность энергий в качестве излучения (кто сказал "аннигиляция"?).
И опять же — см. середину уже процитированного абзаца статьи Дирака:
"... transitions can take place in which the energy of the electron changes from a positive to a negative value ..., the surplus energy, at least 2mc^2 in amount, being spontaneously emitted in form of radiation."
Victor Kleptsyn
М
17:14
Математические байки
Правда, в статье 1929/30 года Дирак ошибочно отождествляет такую дырку с протоном: "We are therefore led to the assumption that the holes in the distribution of negativeenergy electrons are the protons."
Но уже в статье 1931 года он исправляется:
"Subsequent investigations, however, have shown that this particle necessarily has the same mass as an electron and also that, if it collides with an electron, the two will have a chance of annihilating one another much too great to be consistent with the known stability of matter."
(+сноски — H. Weyl, Тамм, Оппенгеймер, Дирак).
Но уже в статье 1931 года он исправляется:
"Subsequent investigations, however, have shown that this particle necessarily has the same mass as an electron and also that, if it collides with an electron, the two will have a chance of annihilating one another much too great to be consistent with the known stability of matter."
(+сноски — H. Weyl, Тамм, Оппенгеймер, Дирак).
Victor Kleptsyn
17:19
И — совершенно блестяще предсказывает позитрон, таким, как мы его знаем. Вот соответствующий участок статьи — обратите внимание, как точно написано, и как замечательно читается!
(From: Paul Adrien Maurice Dirac, Quantised singularities in the electromagnetic field, Proc. R. Soc. Lond. A, 133, pp. 60–72, 01 September 1931)
(From: Paul Adrien Maurice Dirac, Quantised singularities in the electromagnetic field, Proc. R. Soc. Lond. A, 133, pp. 60–72, 01 September 1931)
Victor Kleptsyn
М
18:04
Математические байки
In reply to this message
Хорошо, а при чём всё-таки тут тройное произведение?
Рассмотрим модельную ситуацию — пусть у нас разрешённые энергии это все полуцелые числа. И рассмотрим "вакуумное состояние", когда все состояния с отрицательной энергией заняты, а с положительной — свободны:
Рассмотрим модельную ситуацию — пусть у нас разрешённые энергии это все полуцелые числа. И рассмотрим "вакуумное состояние", когда все состояния с отрицательной энергией заняты, а с положительной — свободны:
Victor Kleptsyn
18:10
А теперь посмотрим на состояния, отличающиеся от вакуумного лишь в конечном числе мест. У них есть две характеристики — энергия E и полный заряд Q (который мы будем считать в "штуках частиц", то есть добавление частицы его увеличивает, а не уменьшает).
(Состояния, отличающиеся в бесконечном числе мест, будут с бесконечной энергией — так что не рассматривать их вполне логично.)
Так давайте составим производящую функцию у этой пары характеристик — просуммируем x^Q*q^E по всем допустимым состояниям. Что получится?
(Состояния, отличающиеся в бесконечном числе мест, будут с бесконечной энергией — так что не рассматривать их вполне логично.)
Так давайте составим производящую функцию у этой пары характеристик — просуммируем x^Q*q^E по всем допустимым состояниям. Что получится?
Victor Kleptsyn
18:20
С одной стороны, можно вычислять эту производящую функцию, работая с каждым энергетическим уровнем по отдельности.
Положительный уровень (2j-1)/2 можно не тронуть — а можно в него добавить частицу; +1 к заряду Q (потому что мы его в частицах считаем; иначе, если бы я сказал "электрон", нужно было бы вычитать 1), и +(2j-1)/2 к энергии.
Отрицательный уровень -(2j-1)/2 можно не тронуть — а можно из него убрать частицу; -1 к заряду Q (потому что мы его в частицах считаем; иначе, если бы я сказал "электрон", нужно было бы добавлять 1), и +(2j-1)/2 к энергии (опять с плюсом — потому что мы убираем частицу с отрицательной энергией).
Итого — производящая функция это вот такое произведение:
Положительный уровень (2j-1)/2 можно не тронуть — а можно в него добавить частицу; +1 к заряду Q (потому что мы его в частицах считаем; иначе, если бы я сказал "электрон", нужно было бы вычитать 1), и +(2j-1)/2 к энергии.
Отрицательный уровень -(2j-1)/2 можно не тронуть — а можно из него убрать частицу; -1 к заряду Q (потому что мы его в частицах считаем; иначе, если бы я сказал "электрон", нужно было бы добавлять 1), и +(2j-1)/2 к энергии (опять с плюсом — потому что мы убираем частицу с отрицательной энергией).
Итого — производящая функция это вот такое произведение:
Victor Kleptsyn
18:25
А если бы мы тут с самого начала пожертвовали симметрией частиц и античастиц и сказали бы, что энергетические состояния это целые числа (а не полуцелые), и заняты в режиме вакуума отрицательные и ноль, а положительные свободны — то получилось бы совсем то, что мы хотели:
Victor Kleptsyn
18:26
In reply to this message
Первая скобка приходит из добавления частиц на каждый свободный уровень j, а вторая — из их убирания с занятых уровней -(j-1).
Victor Kleptsyn
18:30
Но можно считать и по-другому — сначала спросить, "а какой у нас полный заряд Q?".
И тогда — состояние с наименьшей энергией при данном заряде Q это, опять же, "все слева от Q занято, всё справа от Q свободно". И его энергия равна — в "симметричном полуцелом" варианте
1/2 + 3/2 + ... + (2Q-1)/2 = Q^2/2,
а в несимметричном целочисленном —
1 + 2 + ... + Q = Q(Q+1)/2
(если Q отрицательно, то нужно частицы убирать — но правые части всё ещё дают правильный ответ).
И тогда — состояние с наименьшей энергией при данном заряде Q это, опять же, "все слева от Q занято, всё справа от Q свободно". И его энергия равна — в "симметричном полуцелом" варианте
1/2 + 3/2 + ... + (2Q-1)/2 = Q^2/2,
а в несимметричном целочисленном —
1 + 2 + ... + Q = Q(Q+1)/2
(если Q отрицательно, то нужно частицы убирать — но правые части всё ещё дают правильный ответ).
Victor Kleptsyn
18:35
А когда Q уже известен — то любое состояние из состояния с данным зарядом и наименьшей энергией (данного заряда) получается чередой сдвигов частиц на одно состояние вперёд — и способов добавить ещё n единиц энергии как раз p(n), число разбиений n, ибо они индексируются диаграммами Юнга (вне зависимости от значения Q!)
Victor Kleptsyn
18:37
И давайте я тут выложу кадр из видеозаписи курса "Полубесконечная внешняя степень" М. Берштейна в ЛШСМ-2014:
Victor Kleptsyn
18:43
Итого — та же самая производящая функция равна в симметричном-полуцелом случае
Victor Kleptsyn
18:43
А в несимметричном-целочисленном —
Victor Kleptsyn
18:44
In reply to this message
И это и есть то самое тождество, которое мы хотели получить!
Victor Kleptsyn
18:46
In reply to this message
Кстати — вот это же тождество в обзоре Пака; этот вид как раз симметричный — и отличается от выписанного заменой q на q^{1/2} (иными словами, удвоением/делением пополам энергии).
Victor Kleptsyn
18:48
In reply to this message
Кстати, теперь мы на этой фотографии на центральной доске узнаём и выражение A(x,q) во второй строчке. 🙂
И на этом я на сегодня прекращаю дозволенные речи.
И на этом я на сегодня прекращаю дозволенные речи.
Victor Kleptsyn
11 May 2021
М
13:31
Математические байки
t
tropical saint petersburg 11.05.2021 13:11:01
Золотарёв известен в том числе своим простым доказательством квадратичного закона взаимности. Статья Прасолова в МатПросе об этом. Идея простая —
1) символ Лежандра (a/p) выражается как чётность перестановки x->ax на множестве остатков по модулю p.
2) на множестве пар (a,b) остатков по модулям p,q делается подстановка a+pb->qa+b (по китайской теореме об остатках пары остатков это то же самое что остатки по модулю pq).
3) эта подстановка является композицией (a,b)->(a,pb), (a,b)->(qa,b). Поэтому её знак равен (p/q)(q/p).
4) с другой стороны, можно явно посчитать её знак (см картинку).
А вот связь квадратичного закона взаимности с зацеплением узлов (для тех ктов танке тополог)
1) символ Лежандра (a/p) выражается как чётность перестановки x->ax на множестве остатков по модулю p.
2) на множестве пар (a,b) остатков по модулям p,q делается подстановка a+pb->qa+b (по китайской теореме об остатках пары остатков это то же самое что остатки по модулю pq).
3) эта подстановка является композицией (a,b)->(a,pb), (a,b)->(qa,b). Поэтому её знак равен (p/q)(q/p).
4) с другой стороны, можно явно посчитать её знак (см картинку).
А вот связь квадратичного закона взаимности с зацеплением узлов (для тех кто
Victor Kleptsyn
М
15:26
Математические байки
In reply to this message
И давайте я напомню про рассказ про решётку Коркина--Золотарёва = E_8, плотнейшую, как в 2016 году доказала Марина Вязовска, упаковку шаров в 8-мерном пространстве. Как эту решётку можно строить ("вручную" или из пополненного кода Хэмминга) и как она была построена исходно (вместо "размещения решётки в R^8" — "решётка-то это Z^8, но с другой положительно определённой [целочисленной, чётной, унимодулярной] квадратичной формой").
Victor Kleptsyn
13 May 2021
М
13:22
Математические байки
12 мая — день рождения Мариам Мирзахани; этот день в память о ней c 2019-го года отмечается, как день женщин в математике (скажем, вот страница и постер мероприятия в Вышке в 2019-м).
А вот тут — https://may12.womeninmaths.org/ — можно посмотреть на карту мероприятий, которые в этот день (и чуть раньше и позже) проходили/проходят по всему миру. Их много!
Позавчера этому же дню был посвящён коллоквиум Института Эйлера: там лекции были посвящены работам Мирзахани и тематике вокруг; рассказывали Антон Зорич (которого я уже в этом канале упоминал), Элиза Гужар (Elise Goujard; и она тоже тут уже появлялась) и Петр Зограф, и это было круто. И организаторы уже выложили видео лекций!
А мероприятие, которое вчера проводили матфак Вышки и Новая школа, было посвящено Джоан Бирман — рассказу про узлы и косы (Владимир Шастин), её биографии и интервью с ней (Александра Скрипченко). И школьным учительницам — вспоминали, кто на кого и как повлиял.
Ещё — вот программа японского мероприятия; и — какой милый постер сделали итальянцы!
А вот тут — https://may12.womeninmaths.org/ — можно посмотреть на карту мероприятий, которые в этот день (и чуть раньше и позже) проходили/проходят по всему миру. Их много!
Позавчера этому же дню был посвящён коллоквиум Института Эйлера: там лекции были посвящены работам Мирзахани и тематике вокруг; рассказывали Антон Зорич (которого я уже в этом канале упоминал), Элиза Гужар (Elise Goujard; и она тоже тут уже появлялась) и Петр Зограф, и это было круто. И организаторы уже выложили видео лекций!
А мероприятие, которое вчера проводили матфак Вышки и Новая школа, было посвящено Джоан Бирман — рассказу про узлы и косы (Владимир Шастин), её биографии и интервью с ней (Александра Скрипченко). И школьным учительницам — вспоминали, кто на кого и как повлиял.
Ещё — вот программа японского мероприятия; и — какой милый постер сделали итальянцы!
Victor Kleptsyn
14 May 2021
М
16:01
Математические байки
Н
Непрерывное математическое образование 14.05.2021 15:49:10
https://etudes.ru/etudes/angle-trisection/
продолжаем тему математики механизмов — Мат. Этюды про шарнирный механизм для трисекции угла, про Кемпе и теорему о подписи
продолжаем тему математики механизмов — Мат. Этюды про шарнирный механизм для трисекции угла, про Кемпе и теорему о подписи
Victor Kleptsyn
16 May 2021
М
10:52
Математические байки
М
Математические этюды 16.05.2021 10:01:45
Склеим два додекаэдра по грани, потом к одному из них приклеим ещё один додекаэдр, к нему ещё один и так далее. Сможем ли мы получить замкнутую цепочку? Если разрешить у додекаэдра использовать для склейки противоположные грани, то легко придумать замкнутую цепочку из 8 додекаэдров. А если запретить — неизвестно. Вот интересный пример, который, кажется, является замкнутой цепочкой, но на самом деле ошибочен. Зазор между последним и первым додекаэдром меньше 10⁻¹⁰ ребра, тем самым, цепочка не замкнута.
#рисункиМихаилаПанова
#рисункиМихаилаПанова
Victor Kleptsyn
М
11:20
Математические байки
М
МКН СПбГУ 16.05.2021 11:15:01
Приглашаем сегодня с 15-00 до 20-00 присоединяться к мини-конференции, посвящённой юбилею Пафнутия Львовича Чебышева! Лекции рассчитаны на студентов младших курсов и призваны популяризовать красивые и простые идеи П.Л. Чебышева. Подробности и регистрация: https://eimi.ru/chebyshev200
Другие популярные изложения и несколько занимательных фактов из биографии великого математика вы найдёте на его личной странице https://math-cs.spbu.ru/people/chebyshev-pafnutij-lvovich/
Другие популярные изложения и несколько занимательных фактов из биографии великого математика вы найдёте на его личной странице https://math-cs.spbu.ru/people/chebyshev-pafnutij-lvovich/
Victor Kleptsyn
18 May 2021
19 May 2021
М
09:32
Математические байки
Н
Непрерывное математическое образование 19.05.2021 09:09:43
https://mathoverflow.net/q/1924/
«What are some reasonable-sounding statements that are independent of ZFC?»
(и действительно, много довольно неожиданных примеров)
«What are some reasonable-sounding statements that are independent of ZFC?»
(и действительно, много довольно неожиданных примеров)
Victor Kleptsyn
М
21:18
Математические байки
via Дмитрий Швецов — Christophe Ritzenthaler выложил интервью с Жан-Пьером Серром (!); увы, по-французски, но там есть английские субтитры:
https://youtu.be/hPm7_x0DP8Q
https://youtu.be/hPm7_x0DP8Q
Victor Kleptsyn

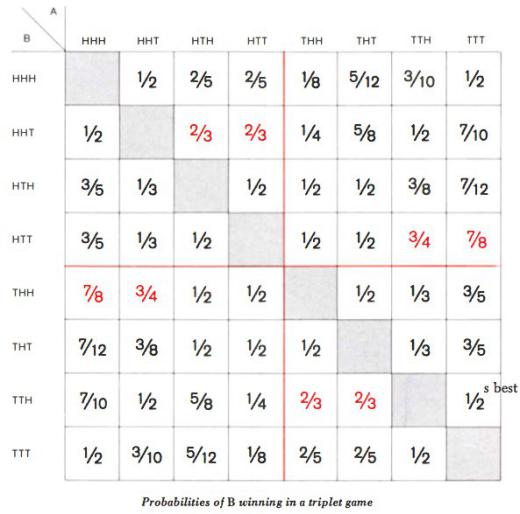
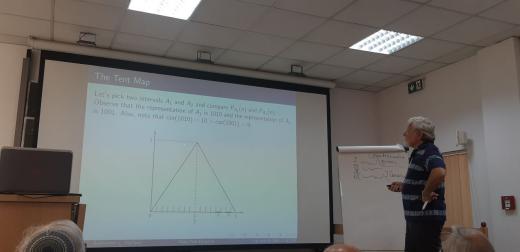

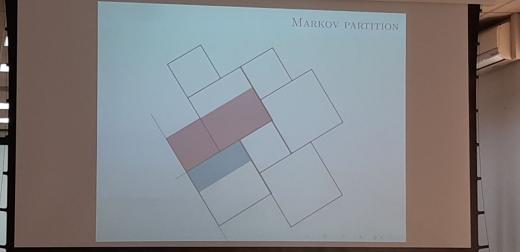



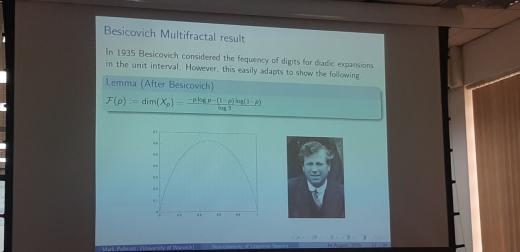
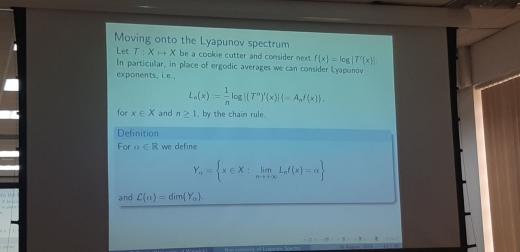






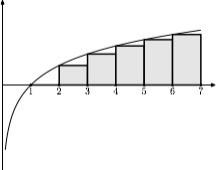
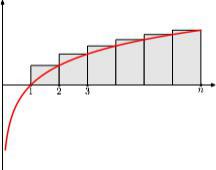
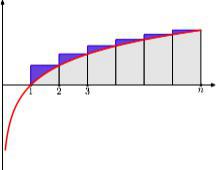

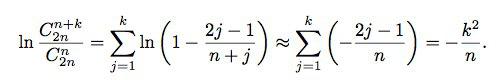
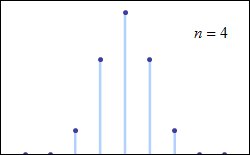
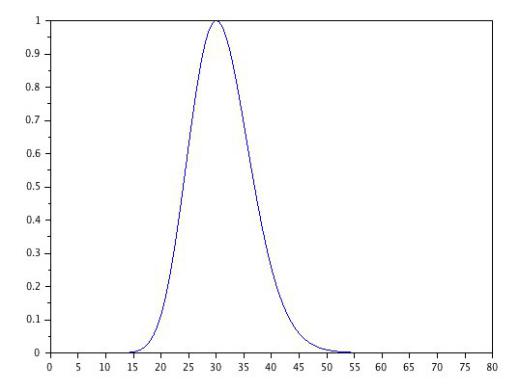
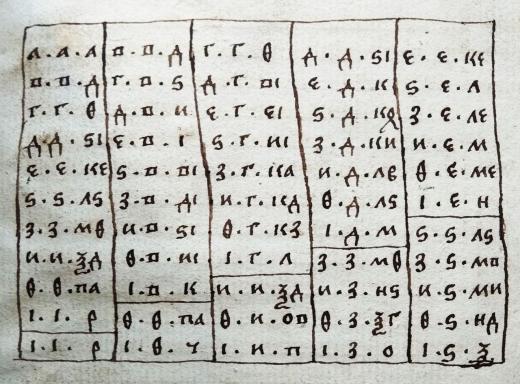


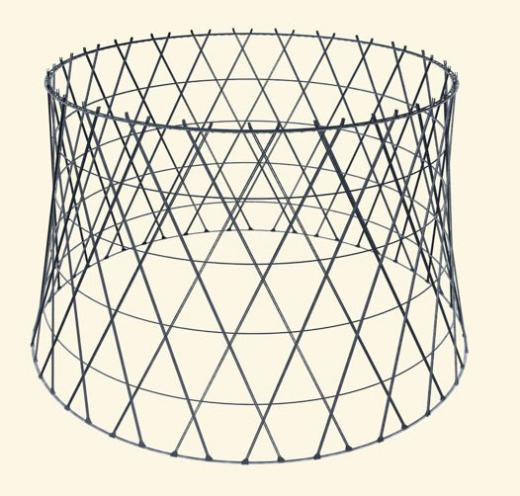
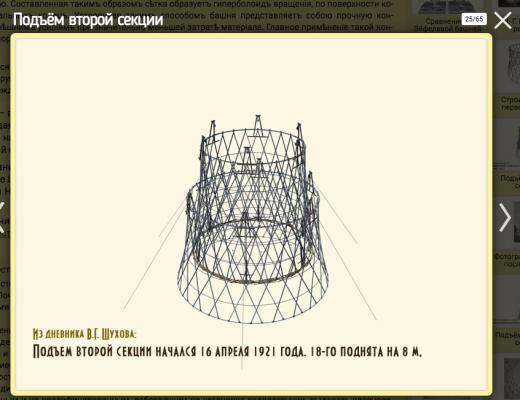







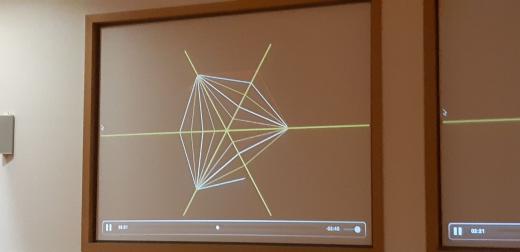


.jpg)




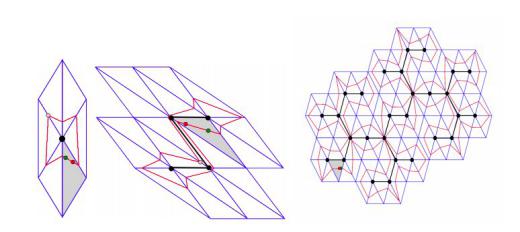






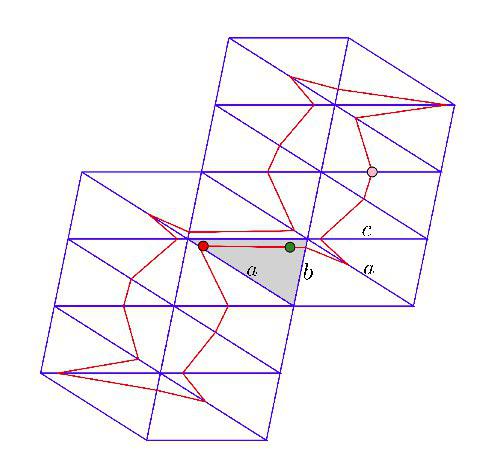
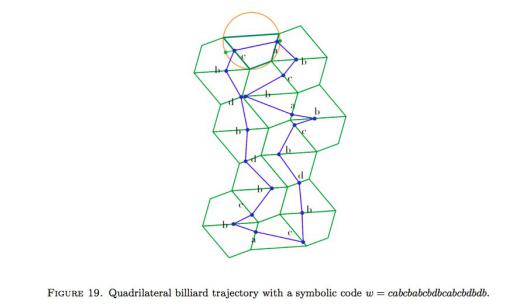
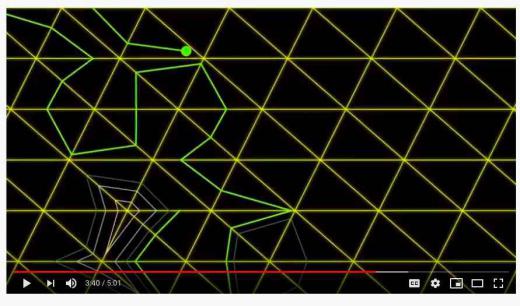
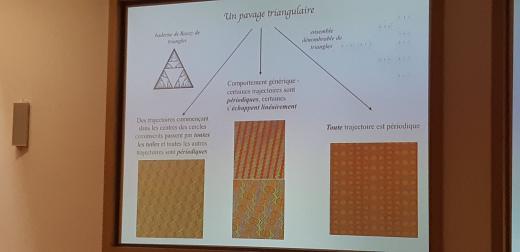
.jpg)
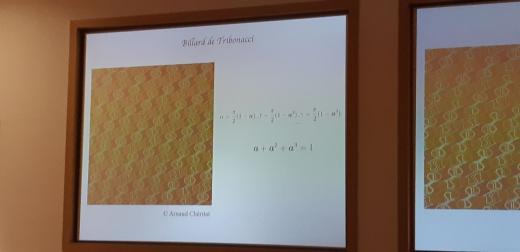

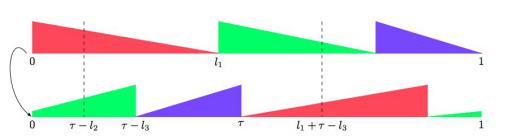

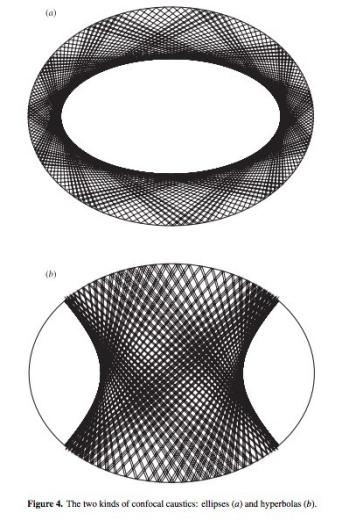
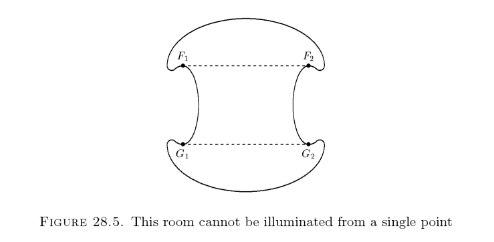


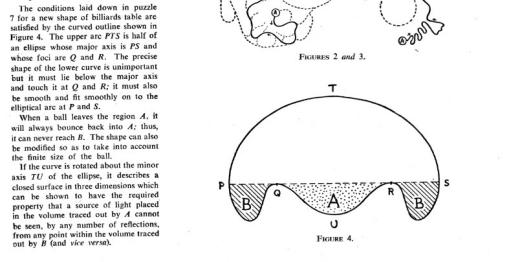
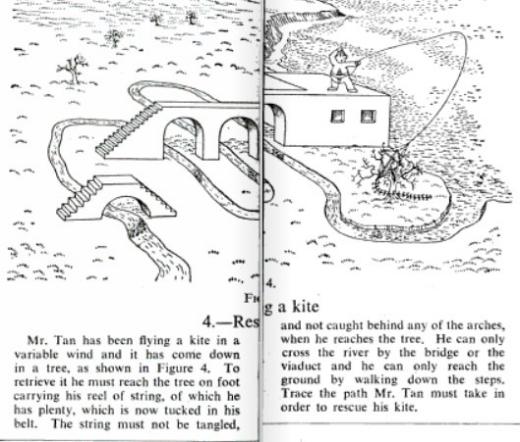
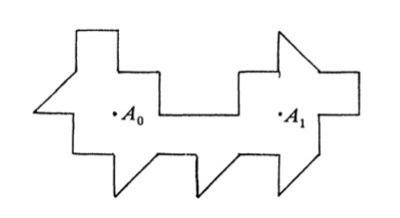

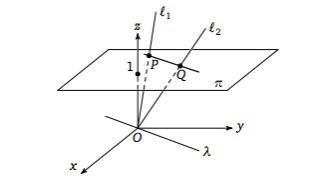














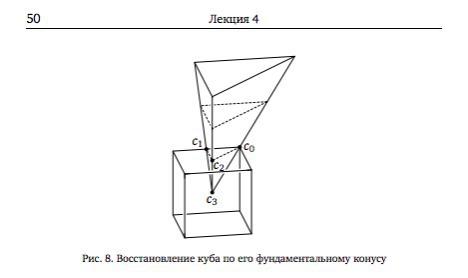



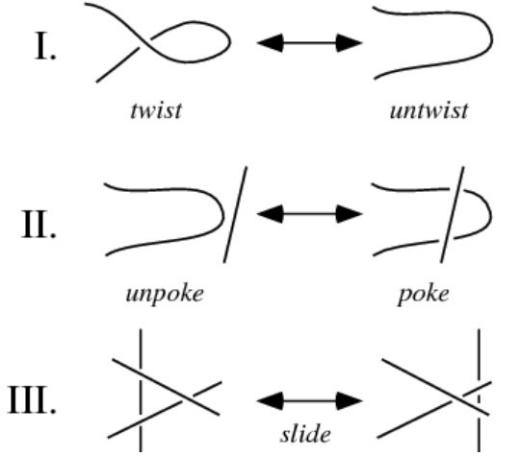
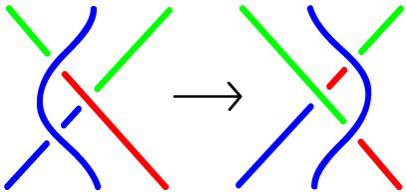

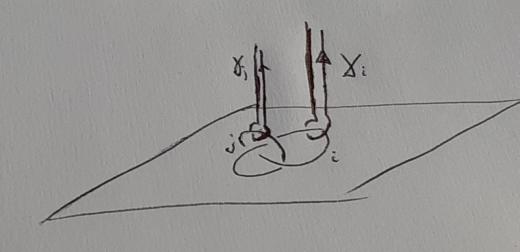



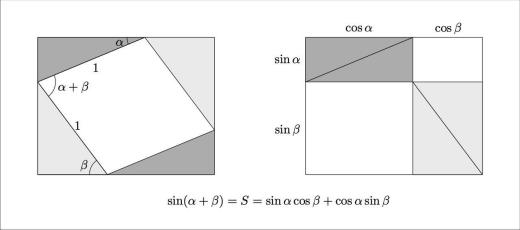

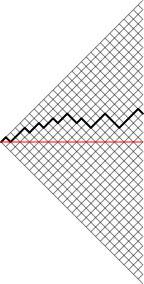
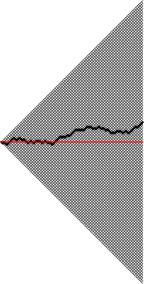
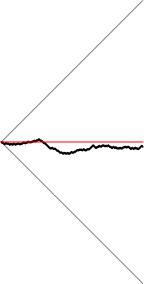

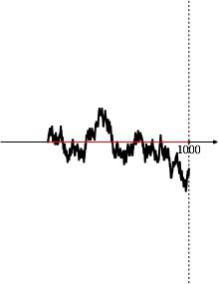

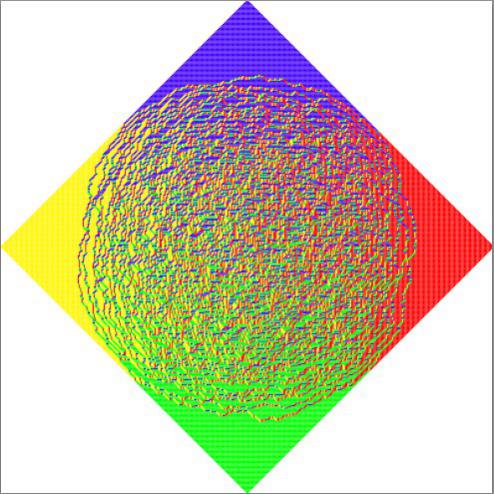

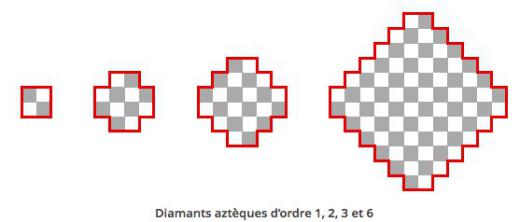
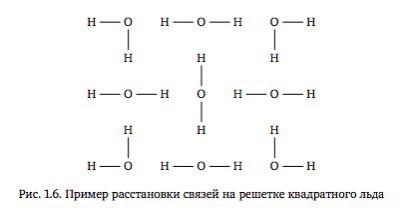
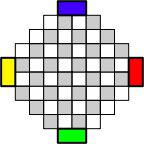
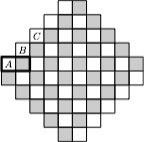
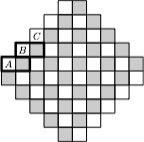
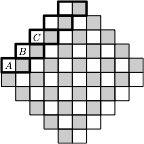
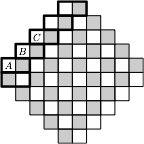
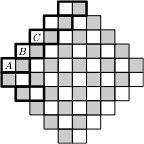
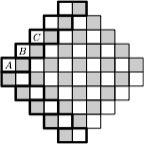




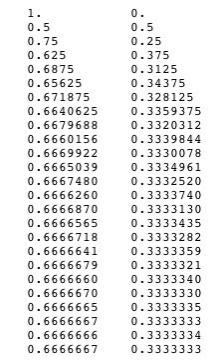





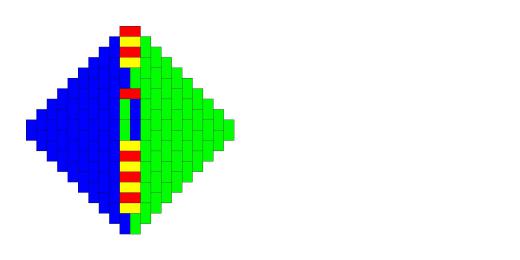
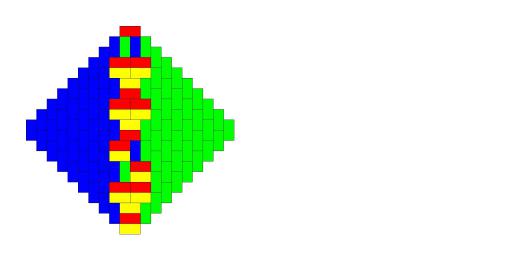
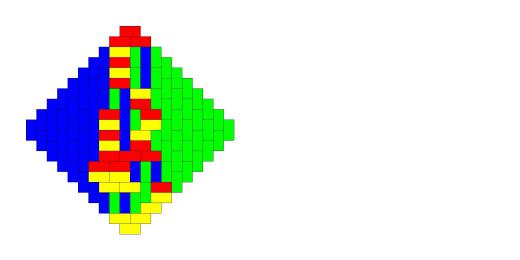
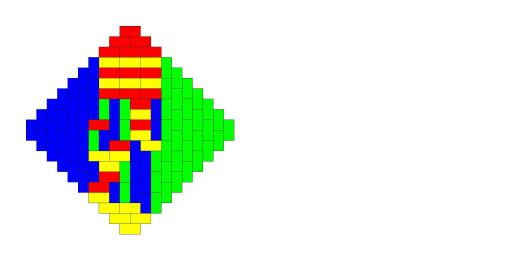
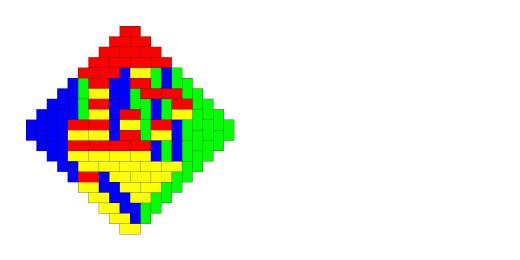

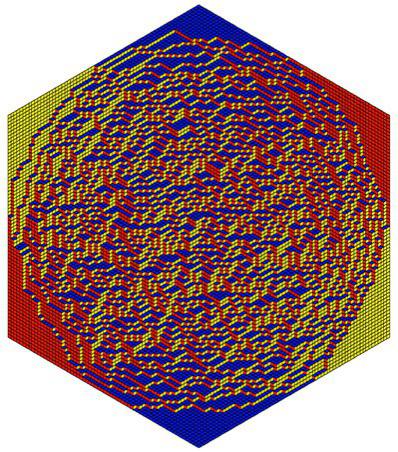

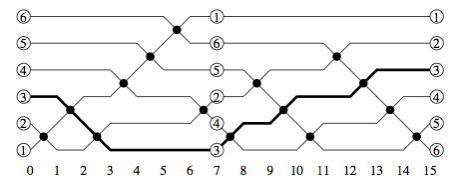
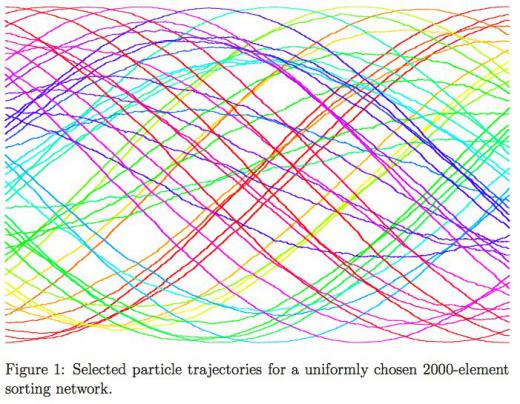
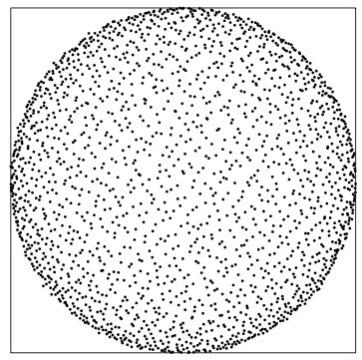

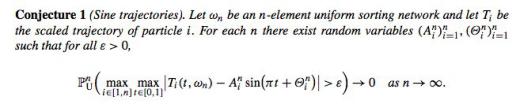

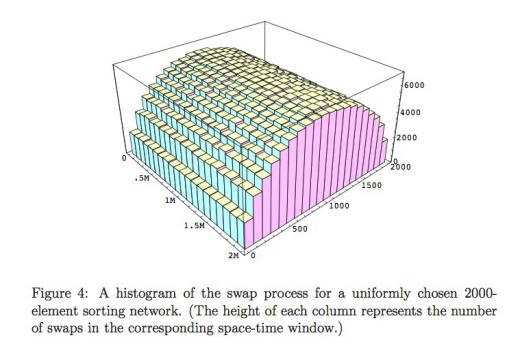

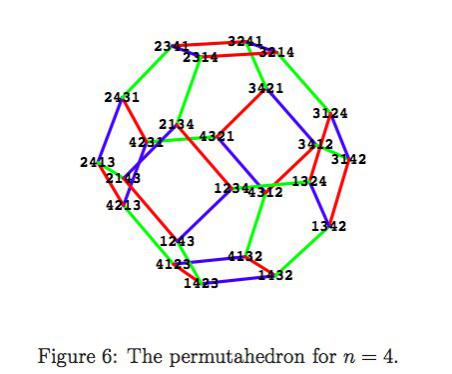
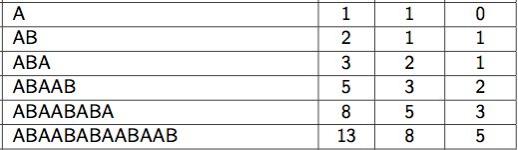

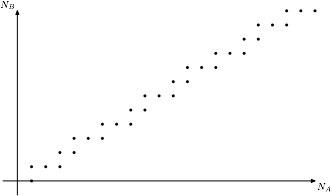
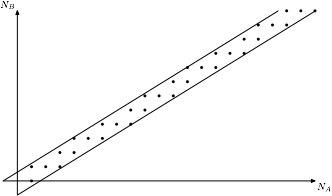
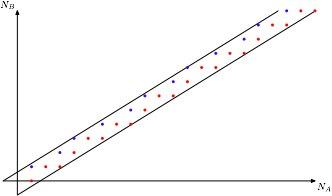
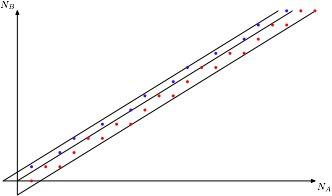
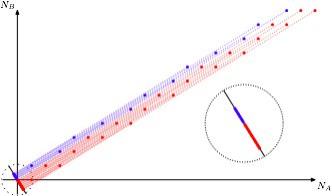
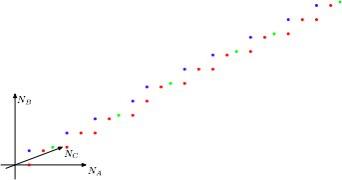

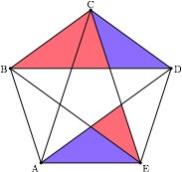
.jpg)
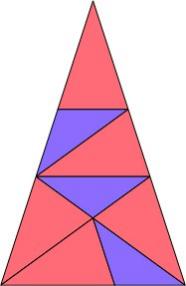
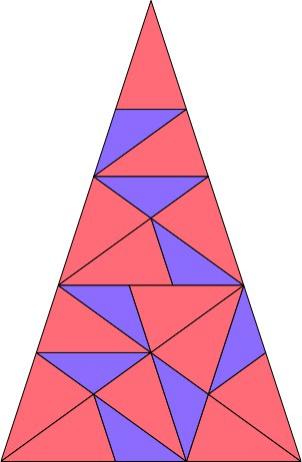

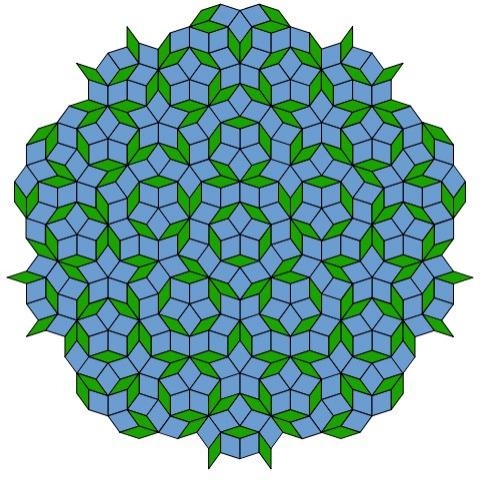
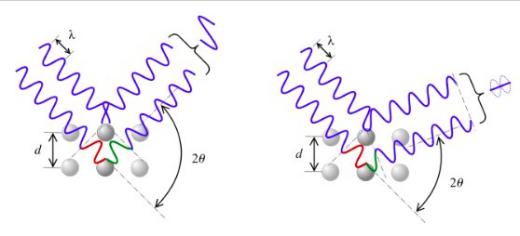


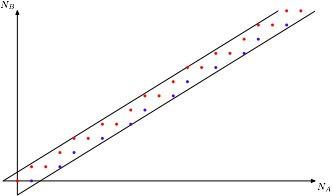
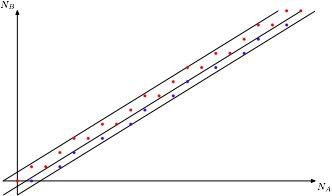
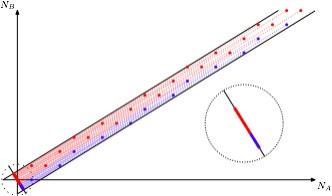
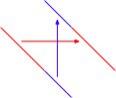
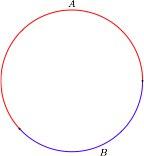
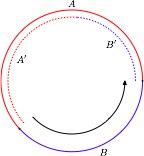








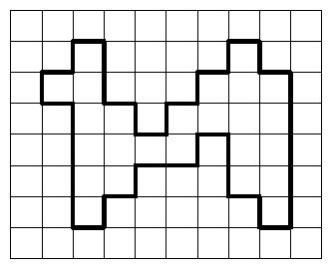





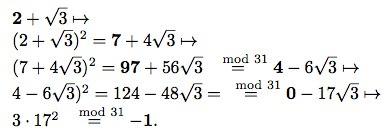



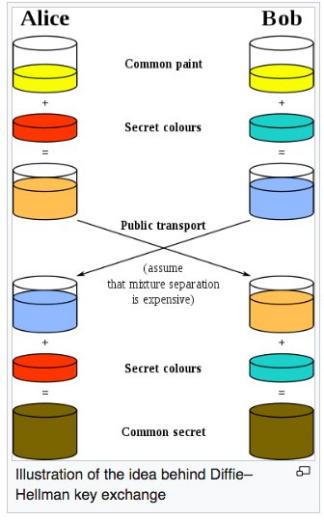
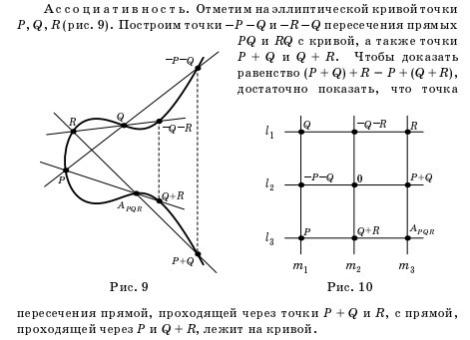

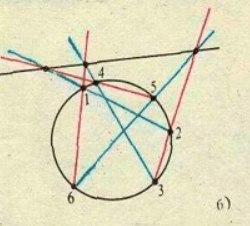

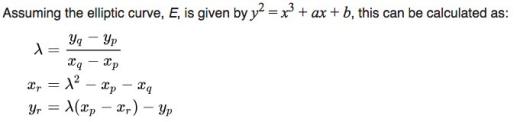

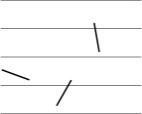




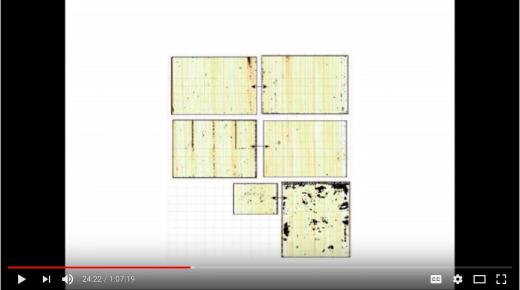




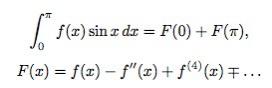
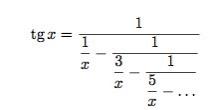
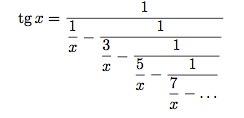
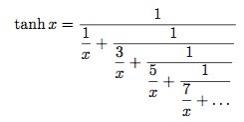
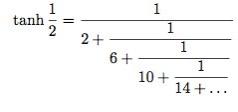
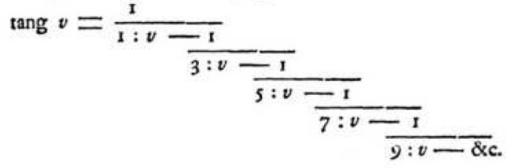
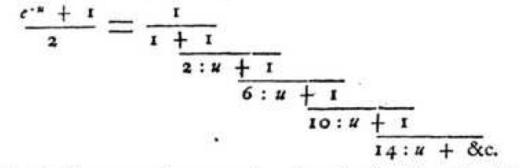
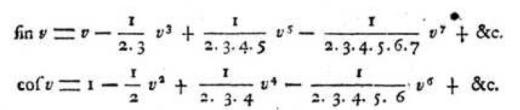
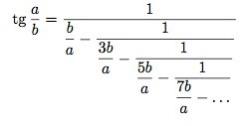
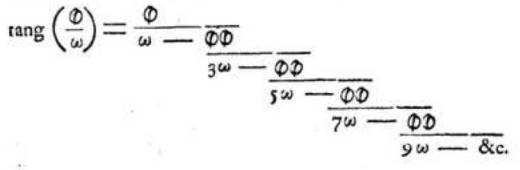
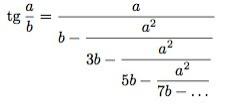

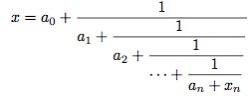
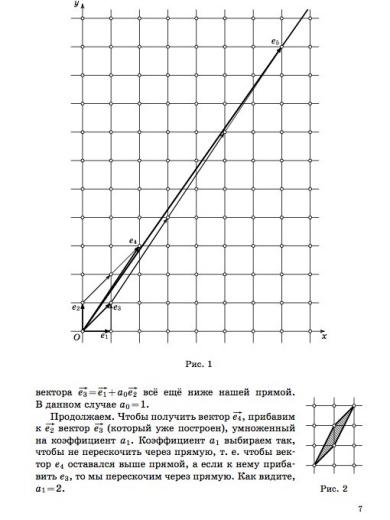
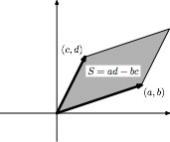
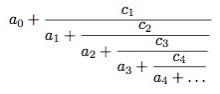


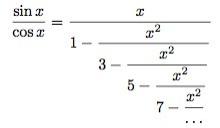
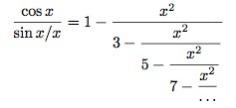
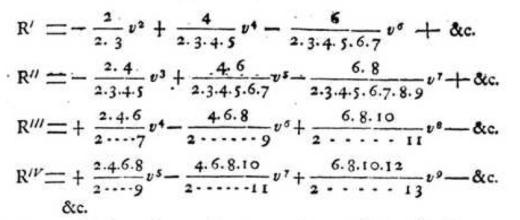

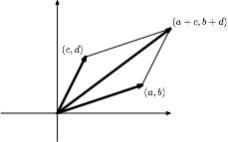
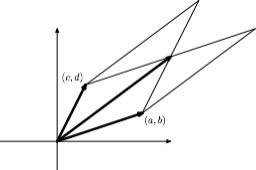



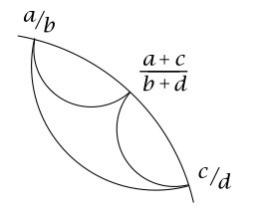
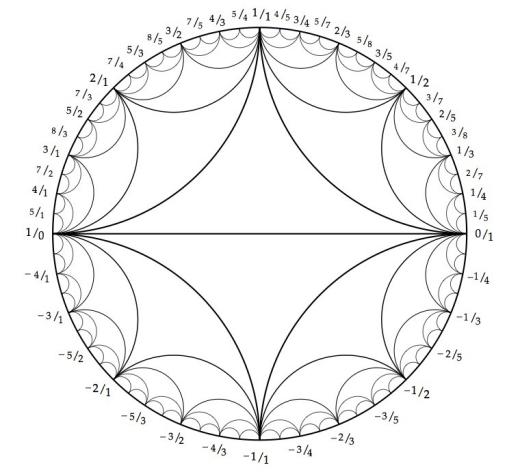

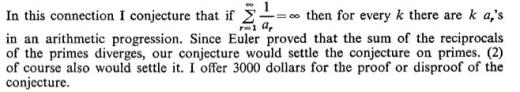



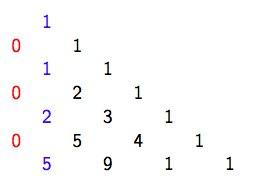
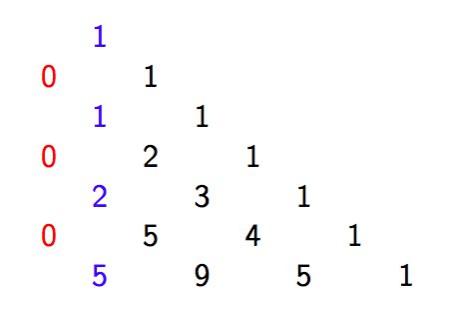
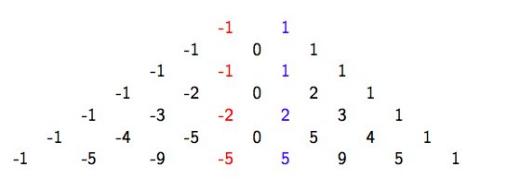


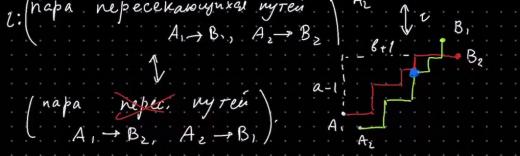
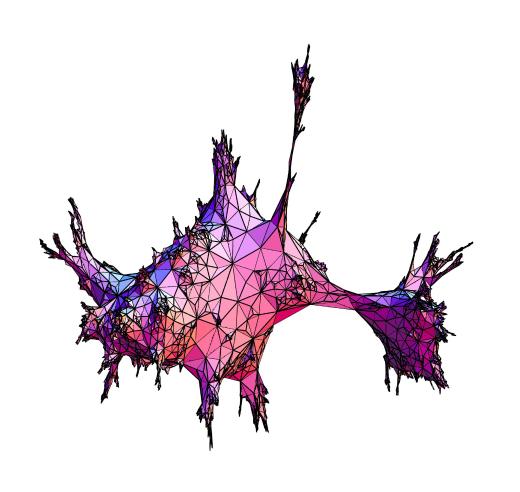

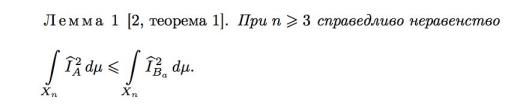




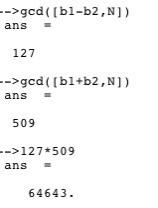
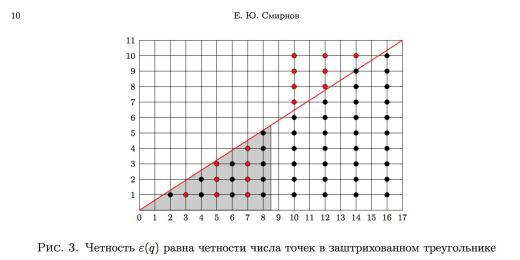











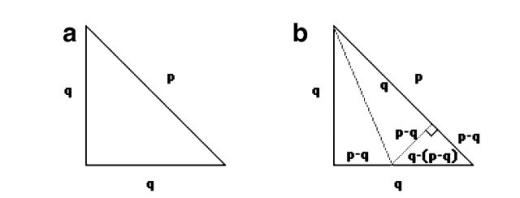
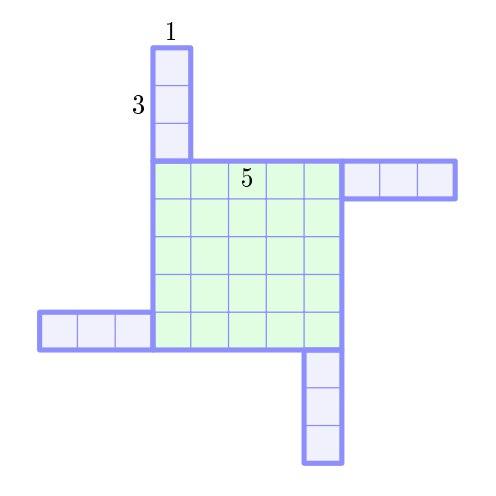
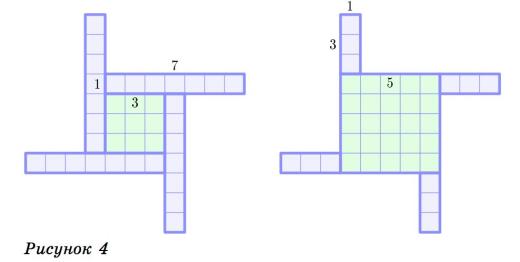
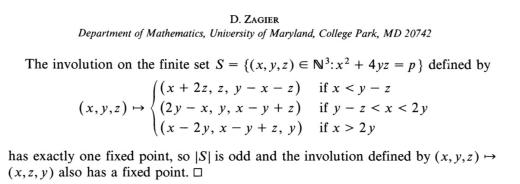
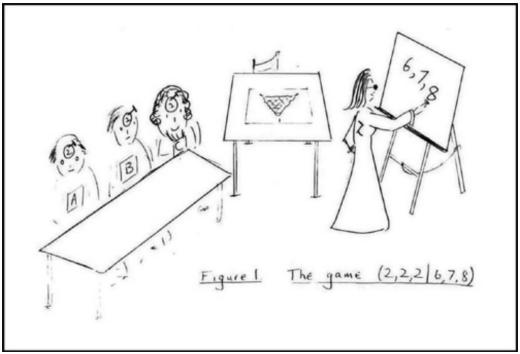


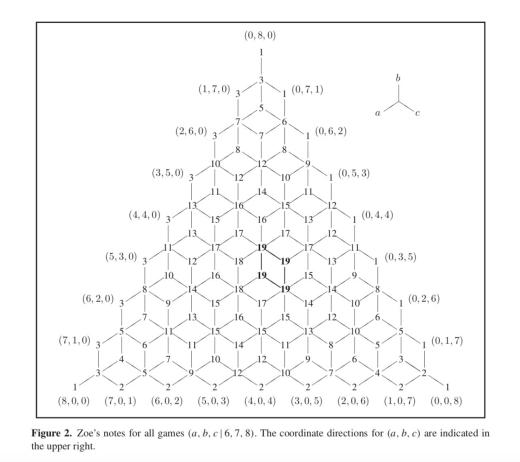
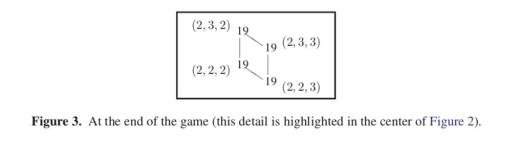





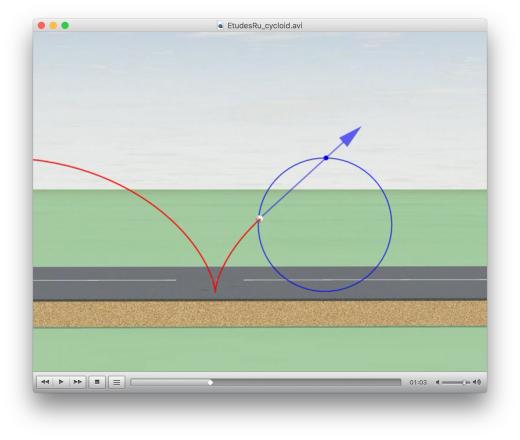
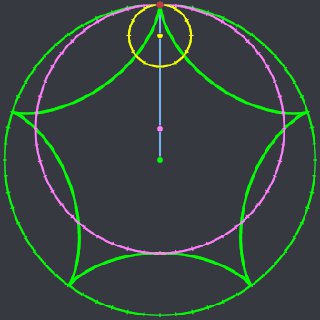
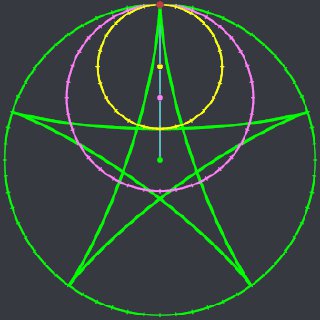
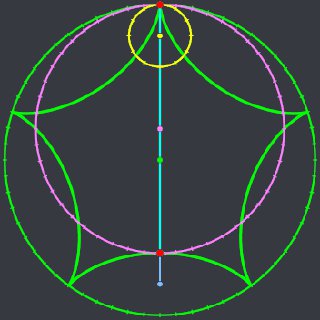

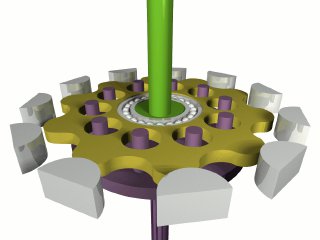
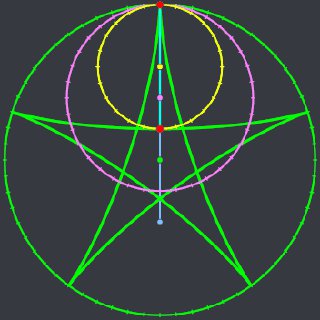

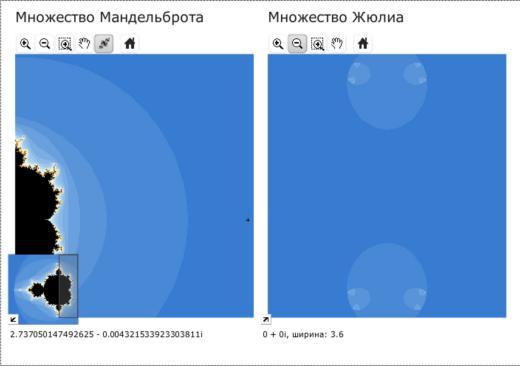
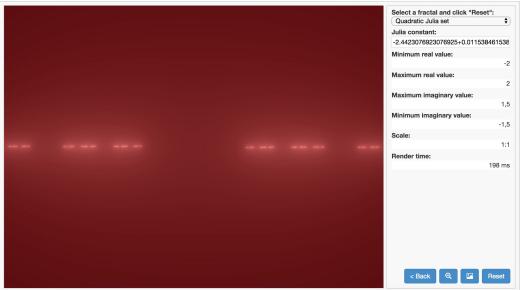
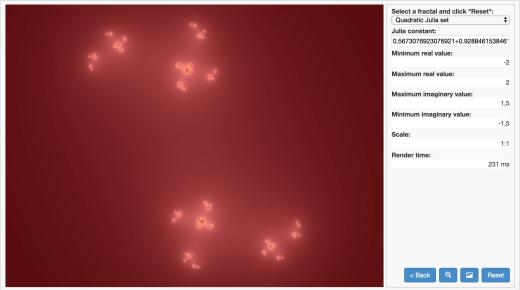





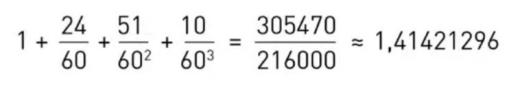
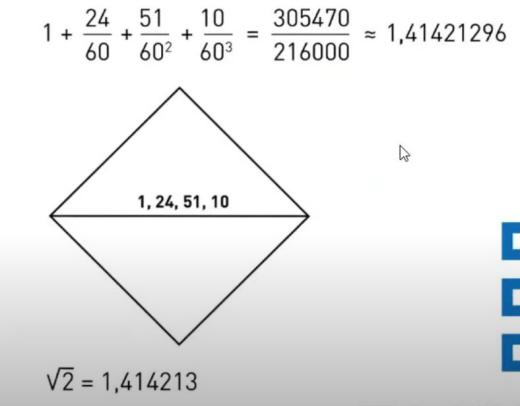








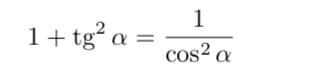
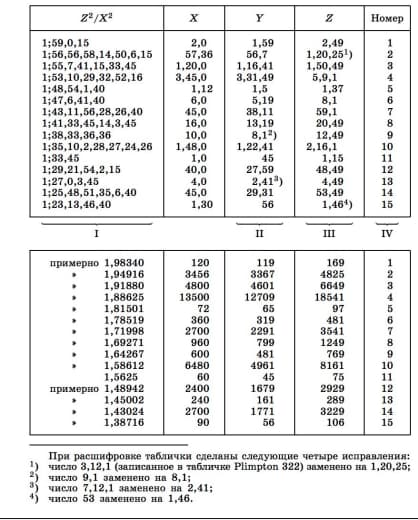

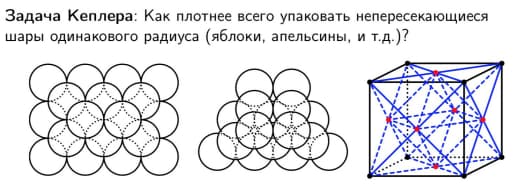
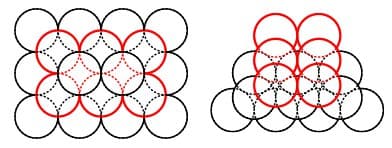


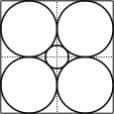
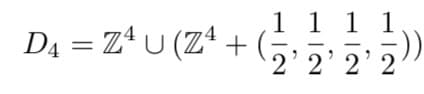





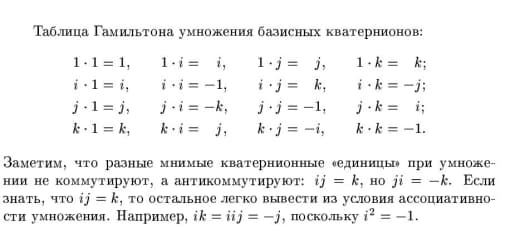
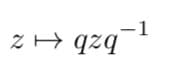






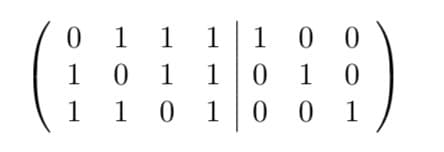



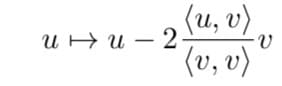
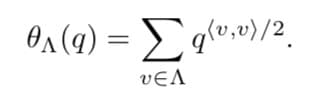
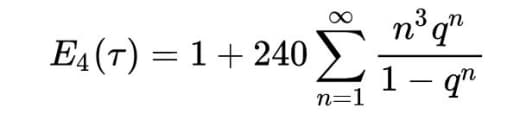

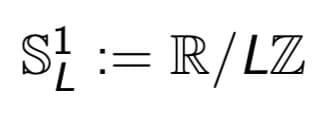
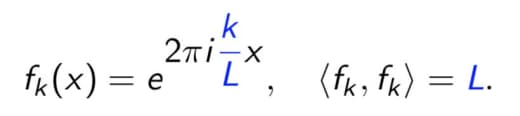
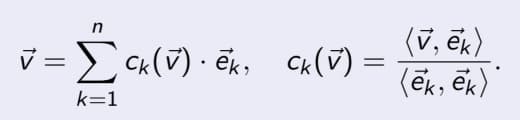
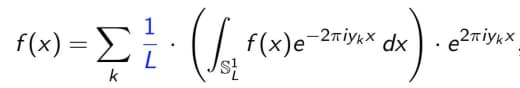
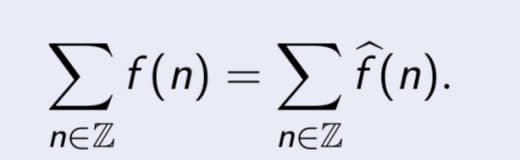
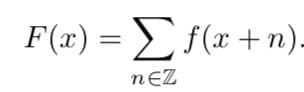
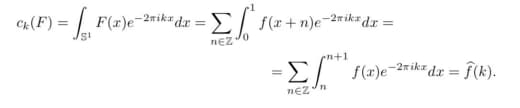
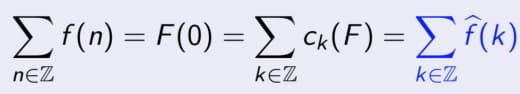
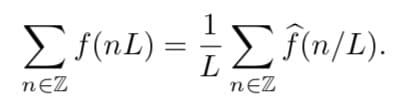
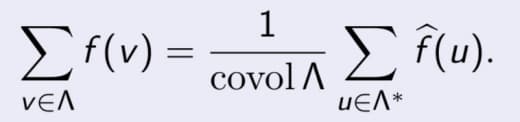


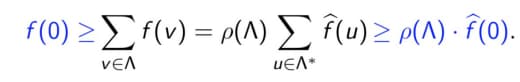

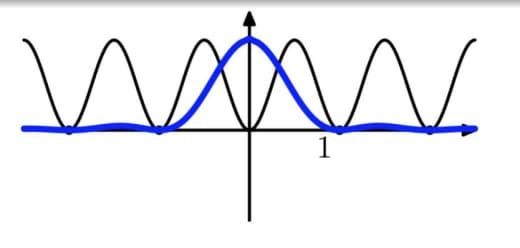
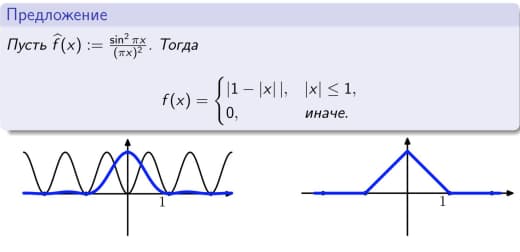

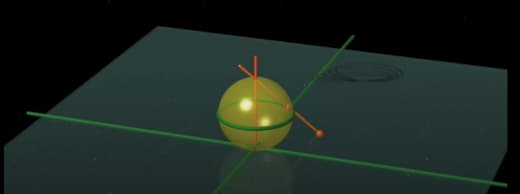

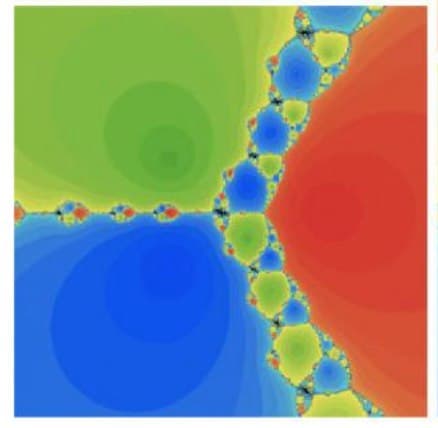

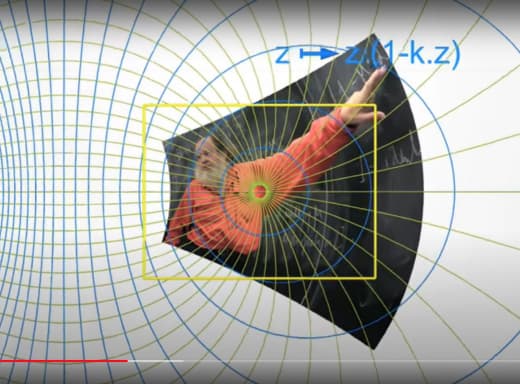


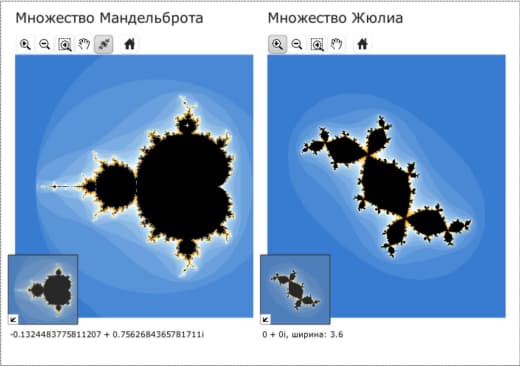
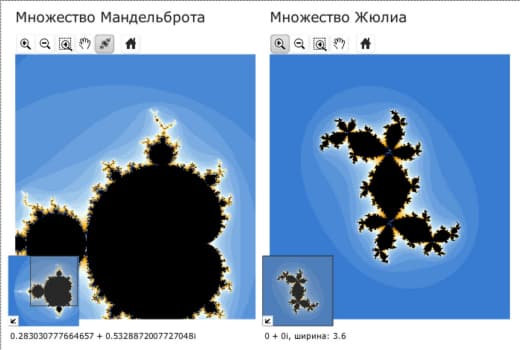
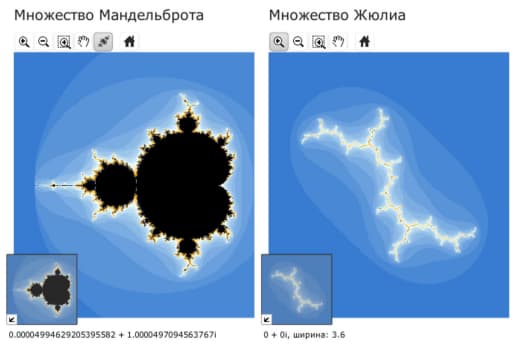
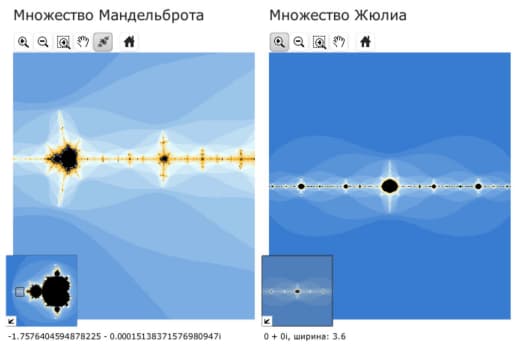
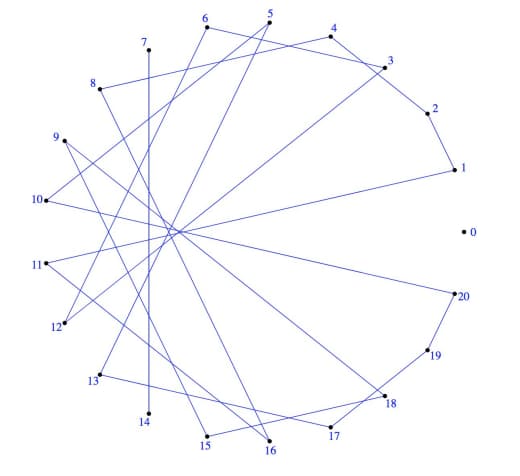
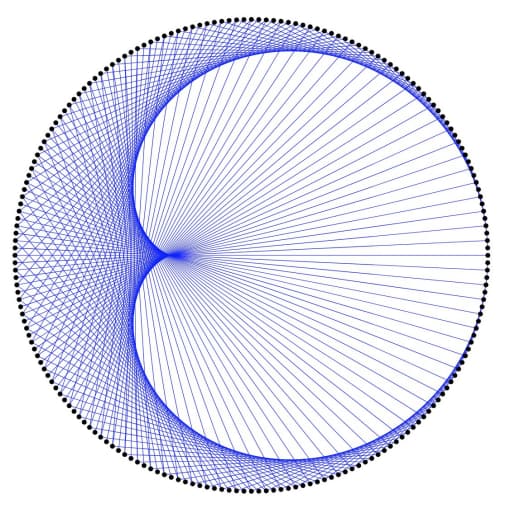


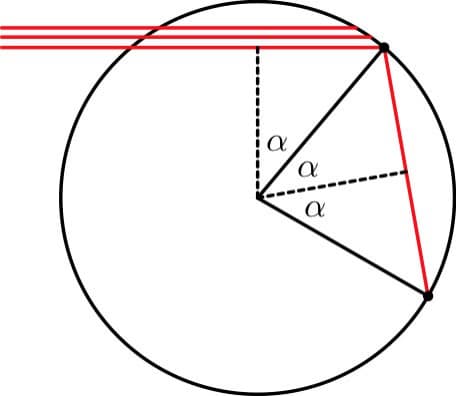









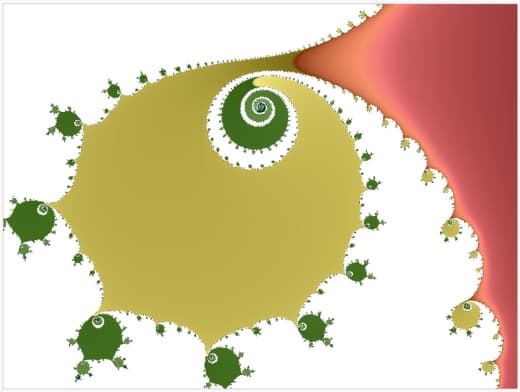


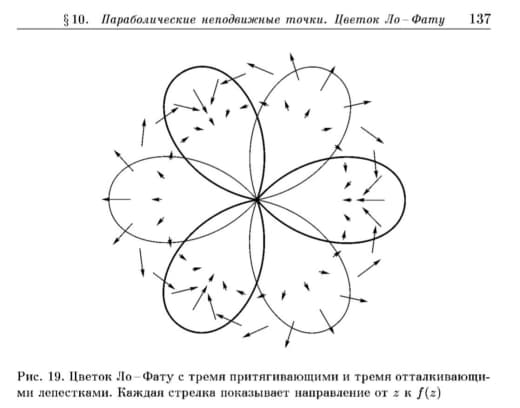




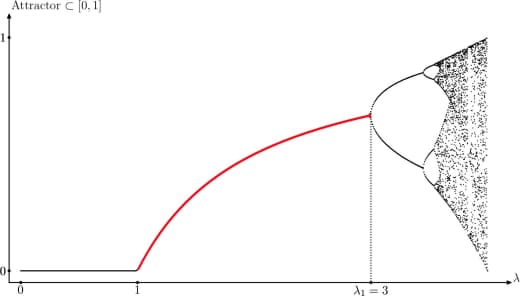
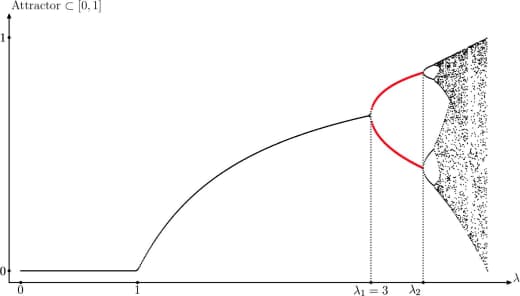

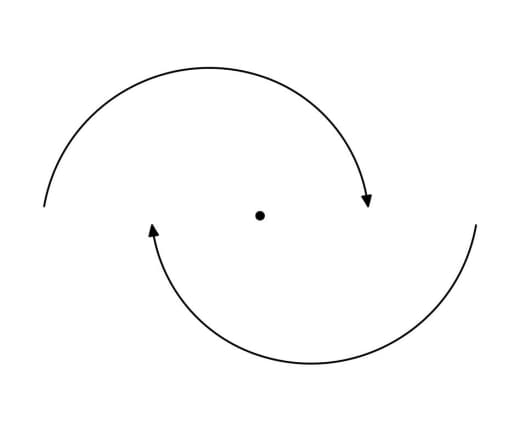
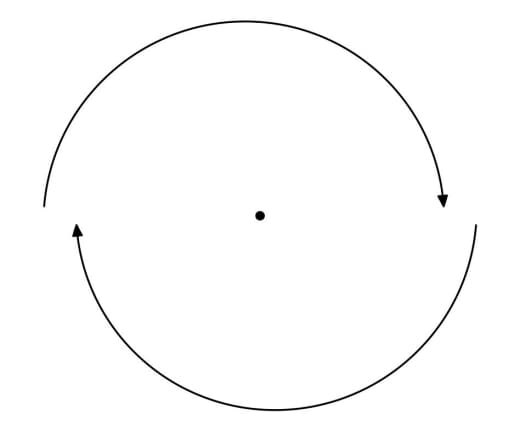
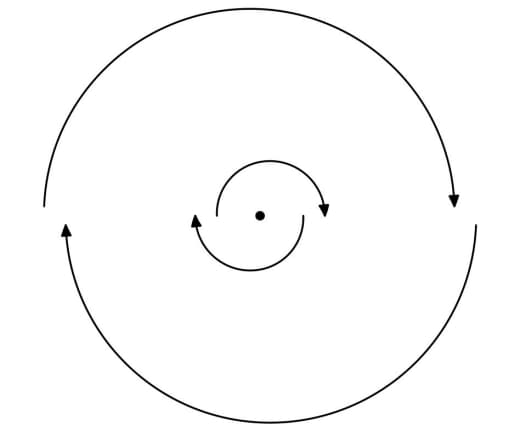
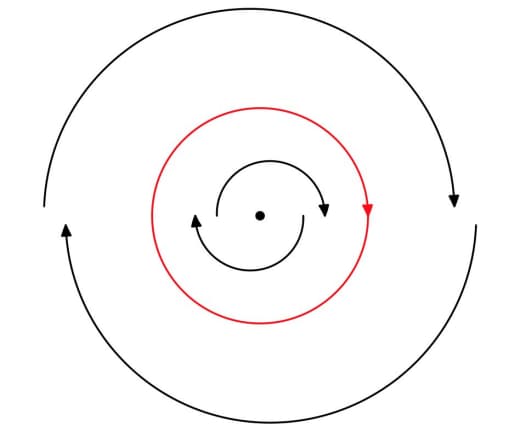

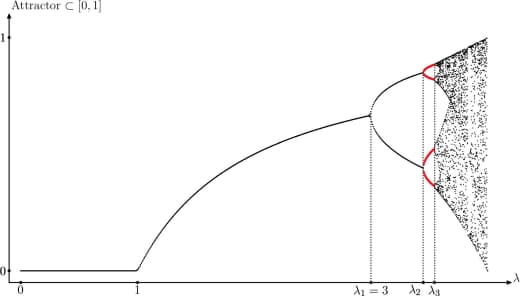


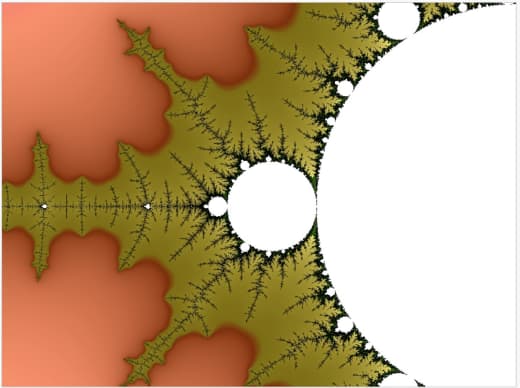
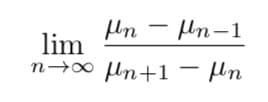

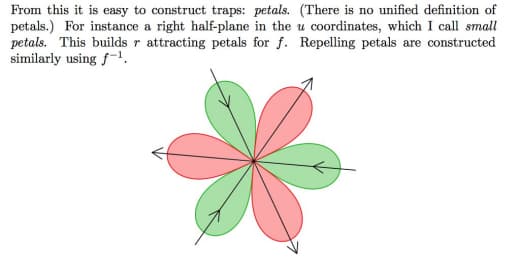

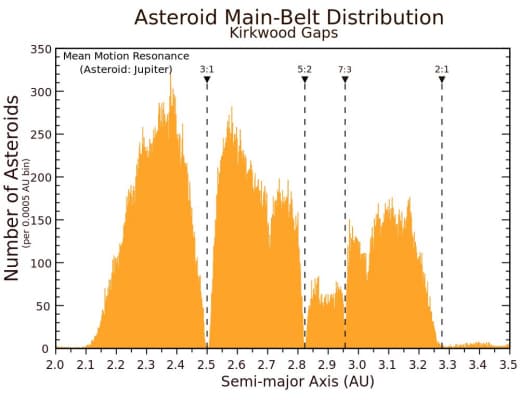




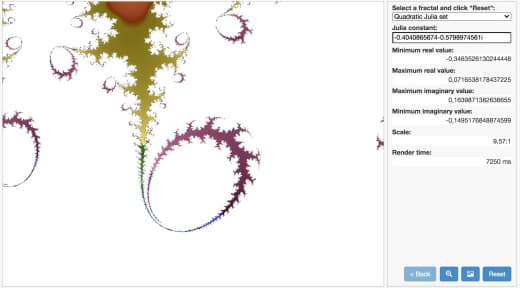
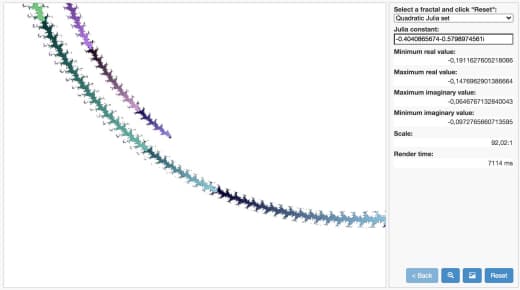
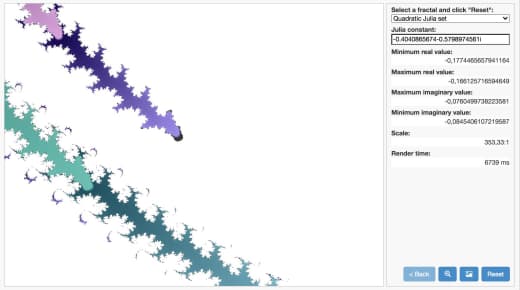


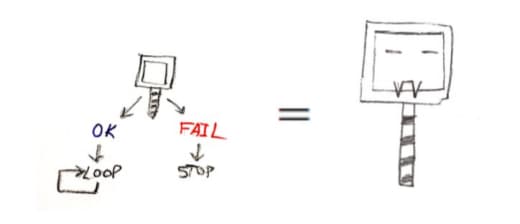
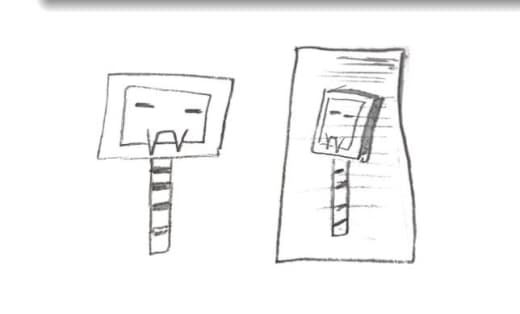



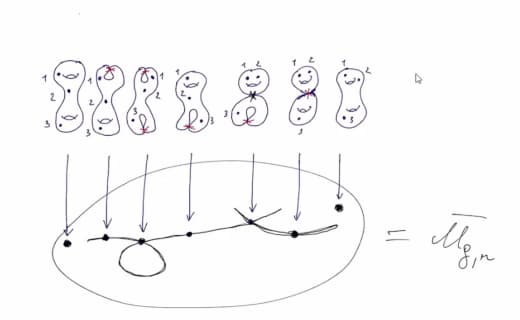
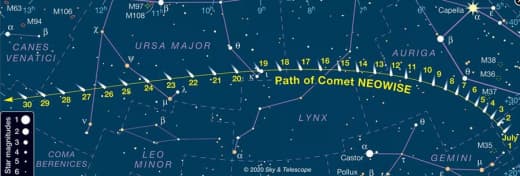


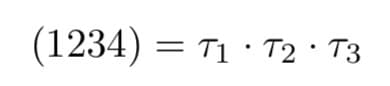
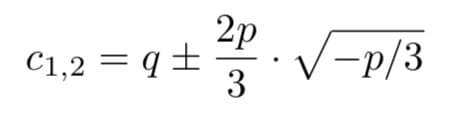
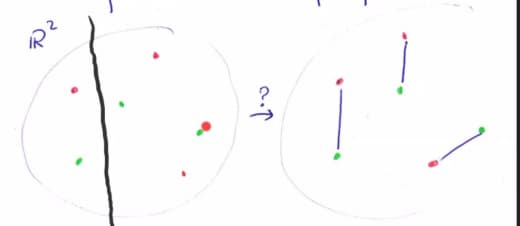
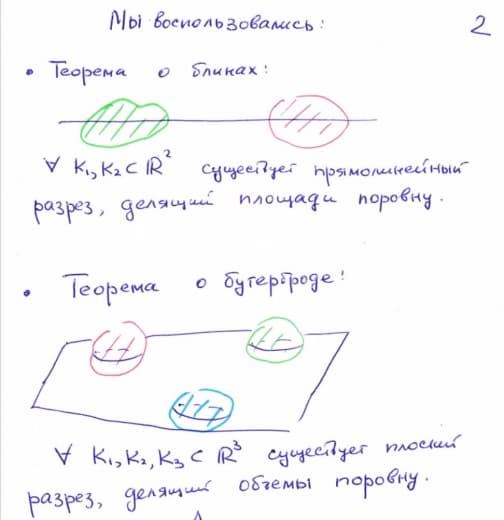
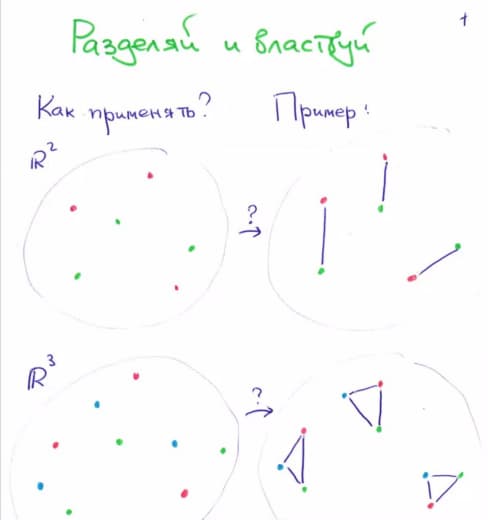
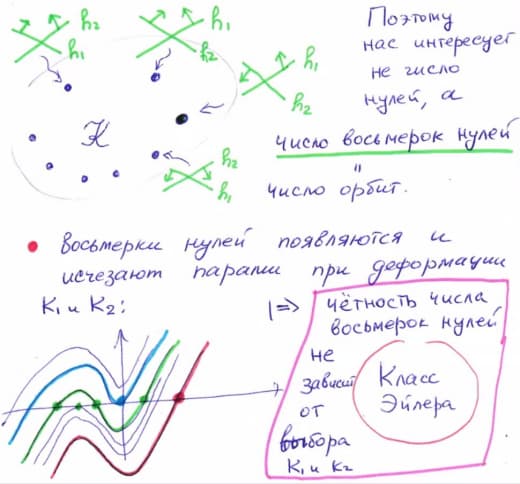

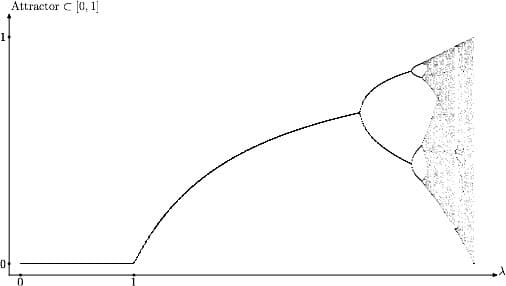
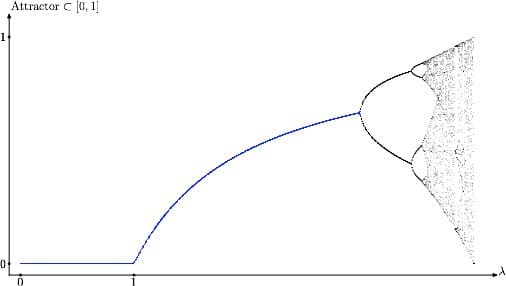
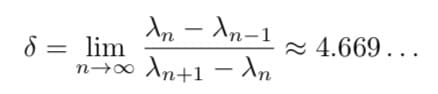
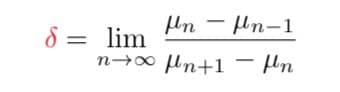

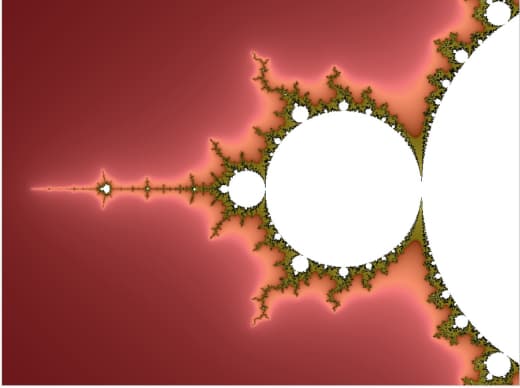





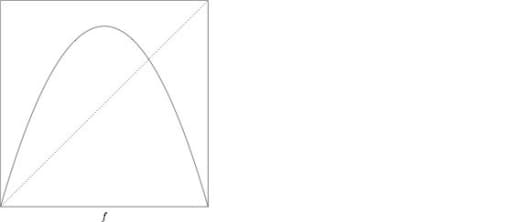
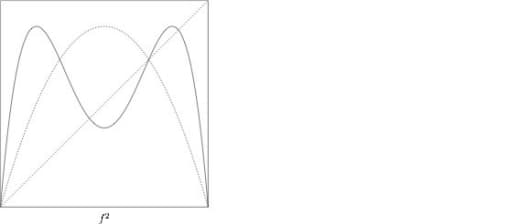
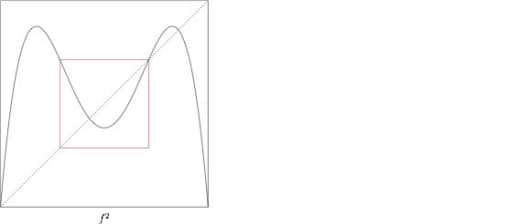
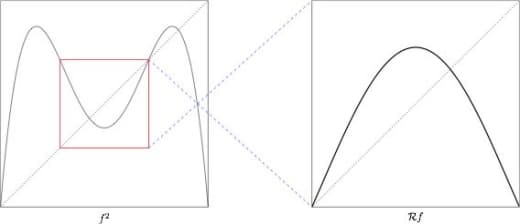
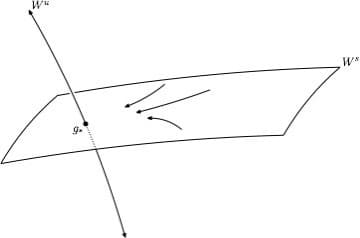
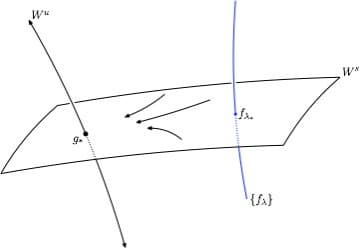
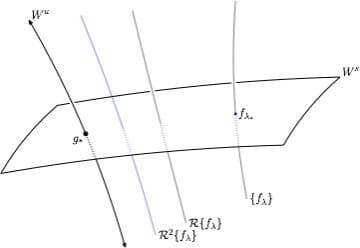
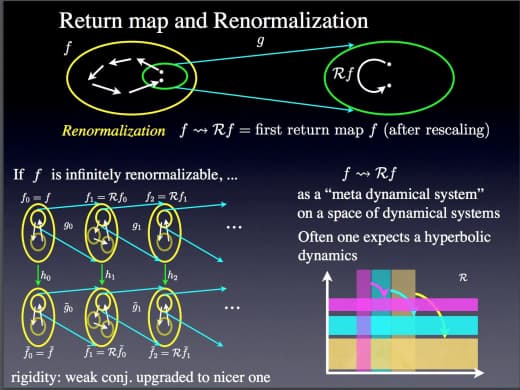
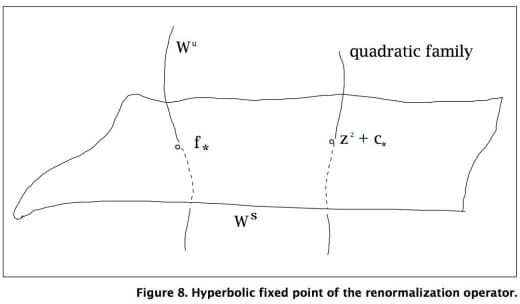






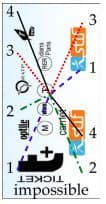

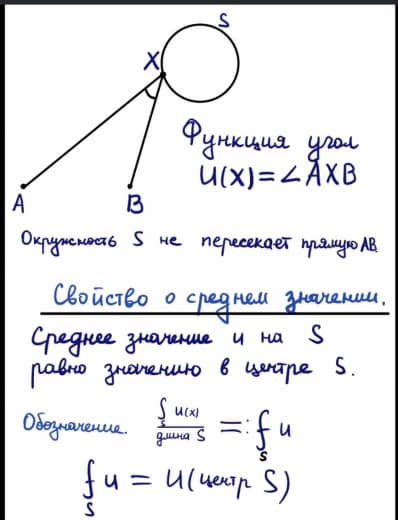

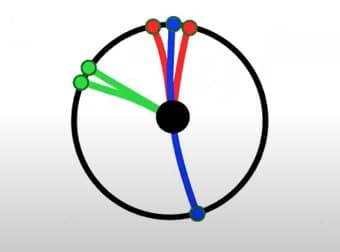
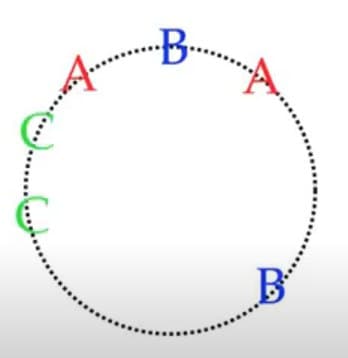
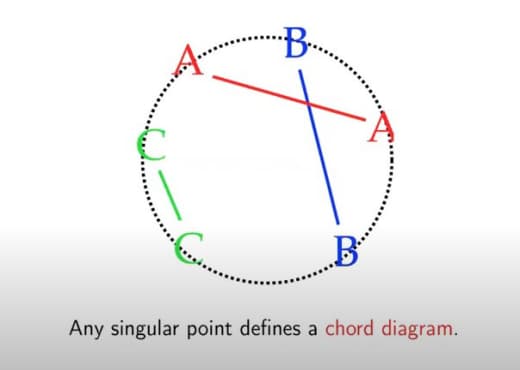
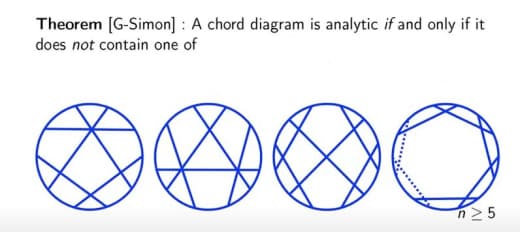

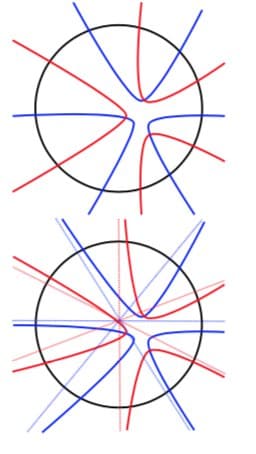
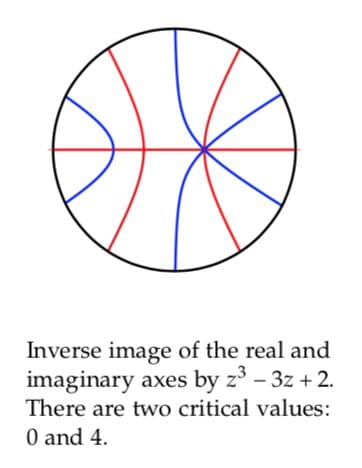
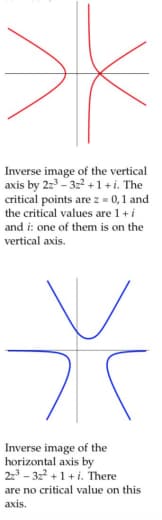



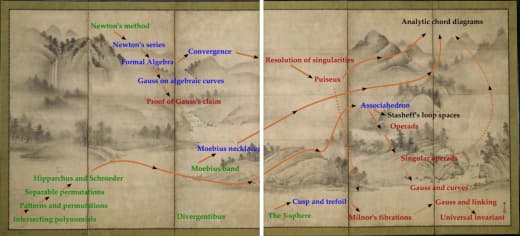






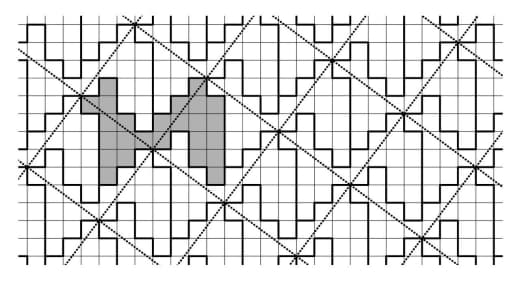
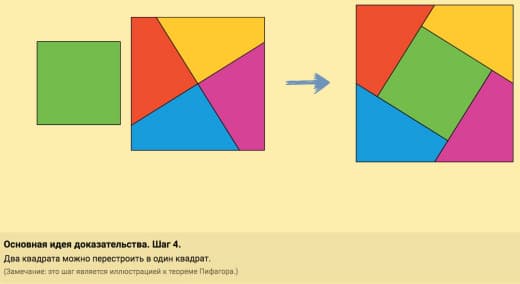





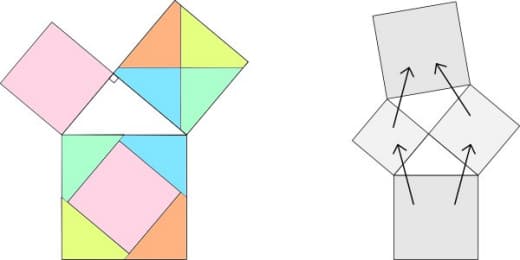



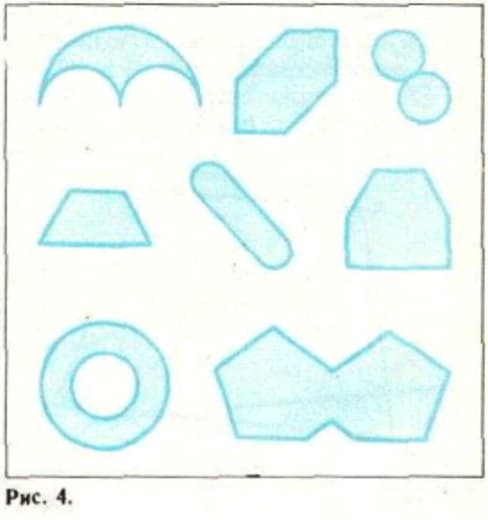
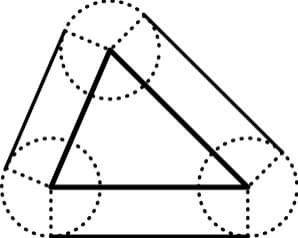
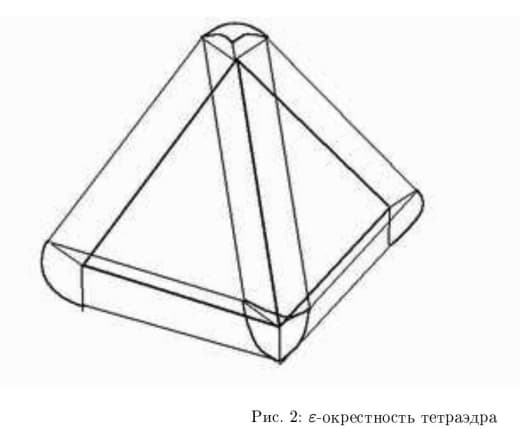
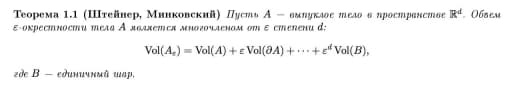

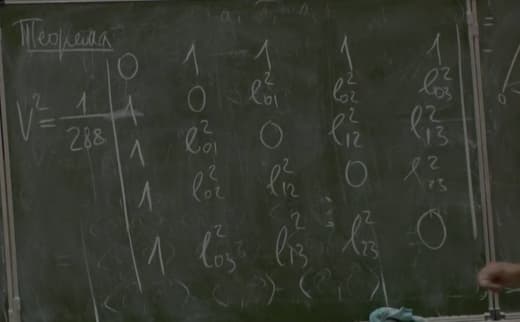
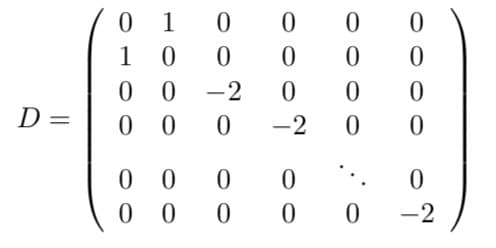










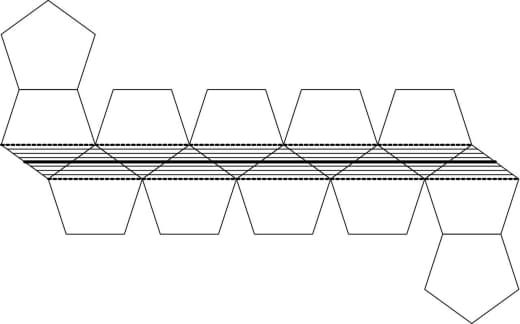


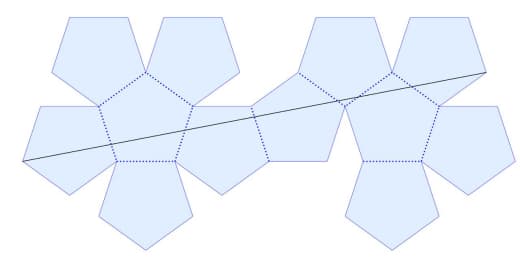
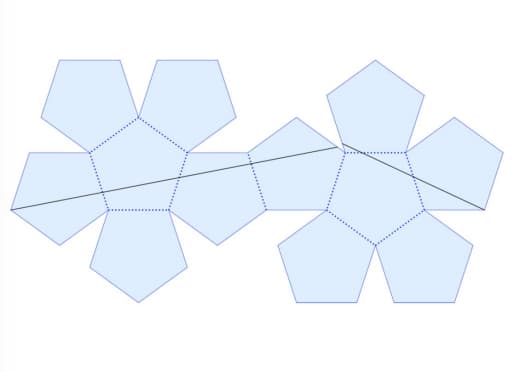
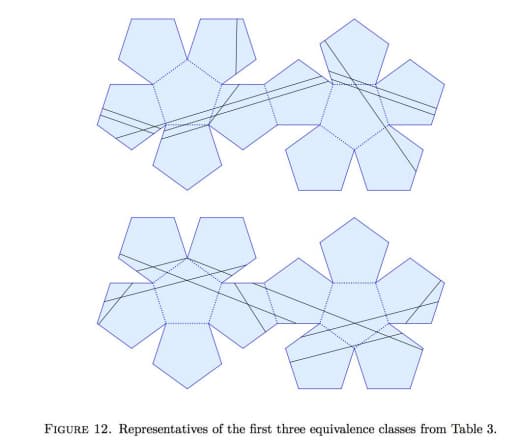
.mp4_thumb.jpg)
.mp4_thumb.jpg)