
Оптическое свойство
эллипса, параболы, гиперболы
Переход между слайдами — стрелочками.
Поместим в одном из фокусов зеркального эллипса лампочку
Поместим в одном из фокусов зеркального эллипса лампочку
и проследим за выпущенными из неё лучами света.
Поместим в одном из фокусов зеркального эллипса лампочку
и проследим за выпущенными из неё лучами света.
Отразившись от эллипса, они соберутся в другом фокусе!
Причём окажутся там одновременно (почему, кстати?).
Оптическое свойство эллипса:
углы касательной с отрезками,
соединяющими точку касания с фокусами, равны.
Оптическое свойство эллипса:
углы касательной с отрезками,
соединяющими точку касания с фокусами, равны.
Как это доказать?
Напомним геометрическое определение эллипса:
эллипс есть множество точек M плоскости, сумма расстояний от которых до данных точек A и B постоянна.
Чтобы доказать оптическое свойство, решим сначала вспомогательную задачу.
Даны две точки по одну сторону от прямой.
Решим вспомогательную задачу.
Даны две точки по одну сторону от прямой.
Мы хотим пройти из A в B, набрав по пути воды из реки l.
Мы хотим пройти из A в B, набрав по пути воды из реки l.
В какой точке M надо набирать воду, чтобы общий путь имел минимальную длину?
Рассмотрим точку B', симметричную точке B.
XB = XB'
Длина AX+XB = AX+XB' минимальна, когда ломаная AXB' превращается в прямую.
Мы хотим пройти из A в B, набрав по пути воды из реки l. В какой точке набирать воду?
Ответ: в точке пересечения l с AB'
(где B' симметрична B относительно l).
Мы хотим пройти из A в B, набрав по пути воды из реки l. В какой точке набирать воду?
Ответ: в точке пересечения l с AB'.
Заодно мы доказали равенство углов.
Мы хотим пройти из A в B, набрав по пути воды из реки l.
Где набирать воду?
Ответ 1: в точке пересечения l с AB'.
Ответ 2: там, где «угол падения равен углу отражения».
Принцип Ферма: свет выбирает кратчайший путь между двумя точками.
Вернемся к доказательству оптического свойства эллипса.
Вернемся к доказательству оптического свойства эллипса.
На эллипсе сумма AM+MB постоянна.
А для точек вне эллипса эта сумма больше,
AX+XB > AM+MB.
В частности, если провести в точке M касательную
к эллипсу, то для любой другой точки X на этой касательной
AX+XB > AM+MB.
Значит, по предыдущей задаче «угол падения равен углу отражения».
...по предыдущей задаче «угол падения равен углу отражения».
Оптическое свойство эллипса доказано.
...по предыдущей задаче «угол падения равен углу отражения».
Оптическое свойство эллипса доказано.
Поместим теперь лампочку в фокус параболы
Поместим теперь лампочку в фокус параболы
и проследим за выпущенными из нее лучами света.
Поместим теперь лампочку в фокус параболы
и проследим за выпущенными из нее лучами света.
После отражения от параболы получится параллельный пучок.
Другими словами, касательная к параболе является биссектрисой угла между отрезком из точки касания в фокус и перпендикуляром из неё на директрису.
Напомним геометрическое определение параболы:
парабола есть множество точек плоскости, равноудаленных от данной точки и данной прямой.
Докажем оптическое свойство параболы.
Докажем оптическое свойство параболы.
Предположим, что биcсектриса не является касательной, а пересекает параболу ещё в одной точке.
Предположим, что биссектриса не является касательной, а пересекает параболу ещё в одной точке.
Соединим точку N с фокусом и с точкой G.
Предположим, что биссектриса не является касательной, а пересекает параболу ещё в одной точке.
Отрезки NG и NF равны (так как треугольники MNG и MNF равны по двум сторонам и углу между ними).
Предположим, что биссектриса не является касательной, а пересекает параболу ещё в одной точке.
Итак, NG = NF.
Но опустим из точки N перпендикуляр NH на директрису.
Предположим, что биссектриса не является касательной, а пересекает параболу ещё в одной точке.
NG = NF. Но и NH = NF (по определению параболы).
Противоречие.
Оптическое свойство параболы доказано.
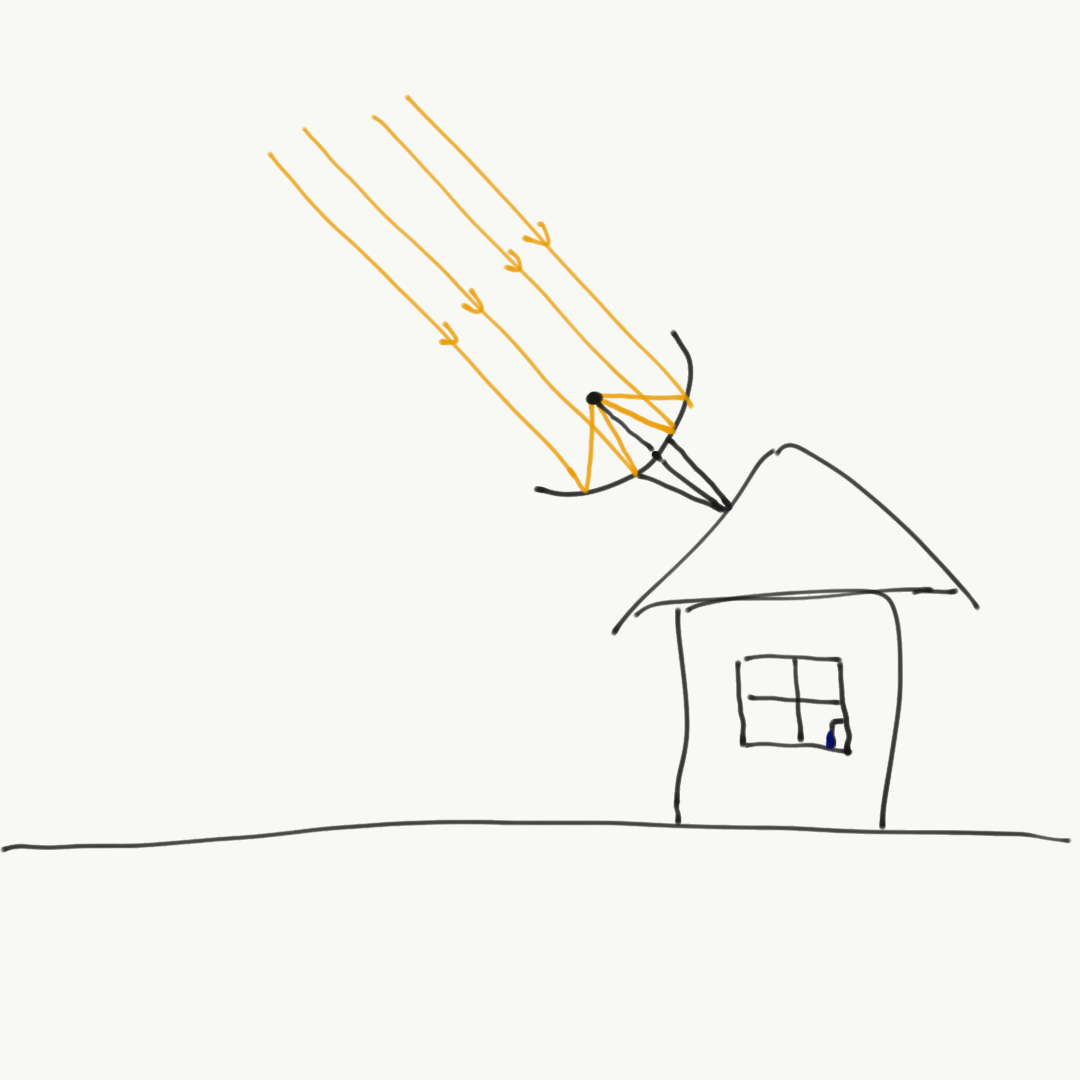
На оптическом свойстве параболы основана работа спутниковых антенн и не только.
Из доказательства видно и кое-что ещё.
Например, что основания перпендикуляров, опущенных из фокуса на касательные, лежат на одной прямой.
То есть если через каждую точку M данной прямой провести перпендикуляр к отрезку, соединяющему M с данной точкой, то возникнет семейство прямых...
…возникнет семейство прямых,
огибающей
которого является парабола.
(А как подобным образом получить эллипс и гиперболу?
К этому мы ещё вернёмся.)
Напомним геометрическое определение гиперболы:
гипербола есть множество точек M плоскости, модуль разности расстояний от которых до данных точек A и B постоянен.
Есть оптическое свойство и у гиперболы.
Попробуйте его доказать.
Для доказательства оптического свойства полезно,
как и в случае эллипса, начать с задачи на максимум:
для какой из точек M прямой
разность AM − MB максимальна?
Зная оптические свойства и эллипса, и гиперболы, несложно доказать (сделайте это!), что эллипс и гипербола с общими фокусами перпендикулярны (т. е. перпендикулярны касательные в точках пересечения).
Вернемся к оптическому свойсту эллипса.
При решении вспомогательной задачи возникала точка,
симметричная фокусу относительно «реки» (касательной).
Как выглядит ее траектория?
Точка, симметричная фокусу относительно касательной движется по окружности с центром во втором фокусе.
Точка, симметричная фокусу относительно касательной движется по окружности.
Значит, основание перпендикуляра, опущенного из фокуса на касательную, тоже движется по окружности (вдвое меньшей).
Основание перпендикуляра, опущенного из фокуса эллипса на касательную, движется по окружности.
Основание перпендикуляра, опущенного из фокуса эллипса на касательную, движется по окружности.
То есть эллипс получается как огибающая соответствующего семейства прямых.
Похожим образом возникает
как огибающая семейства прямых
и гипербола.
версия 1.0.3 (июль 2018)
больше можно узнать из книги
«Прямые и кривые»
Н. Б. Васильева и В. Л. Гутенмахера
Картинки — М. Панов.
Разговоры — Г. Мерзон, М. Панов.
другие истории: про котёнка на лестнице